Data Clustering Using Wave Atom

Published Online August 2012 in MECS

Clustering is one of the most important tasks in data analysis. It has been used for decades in image processing and pattern recognition. Clustering is a process of dividing a set of given data into groups, or clusters, such that all data in the same group are similar to each other, while data from different clusters are dissimilar [2]. In recent year more attention has been paid to spatial data mining in the last decade [13], in order to recognize a considerable information or knowledge from spatial databases. Usually the spatial relationships are implicit in nature. Spatial clustering has present an important role in the process of spatial data mining. It aims to distinguish a spatial database into several clusters without any prior knowledge (e.g., probability distribution and the number of clusters). spatial points in the same cluster are similar to one another and dissimilar to the points in different clusters. Spatial clustering can be generally employed to segment geographic regions with different characteristics and extract meaningful spatial patterns. Spatial clustering also can help to generalize the aggregate point features and find the optimal positions of the public facilities.

Due to the huge amount of spatial data, an important confrontation for clustering algorithms is to achieve good time efficiency. due to the diverse nature of the spatial objects, the clusters may be of arbitrary shape They may be nested within one another, may have holes inside, or may possess concave shapes. The best clustering algorithm should be able to identify clusters irrespective of their shapes or relative positions and should not get affected by the different ordering of input data and should produce the same clusters. In other word, it should be insensitive to ordered of input data. Another important issue is the handling of noise or outliers. Outlier in statistics, is one that appears to deviate markedly from other members of the sample in which it occurs the Identification of this object (outliers) can lead to the determination a hidden knowledge about the data. In other word spatial outliers are those observations which are inconsistent with their surrounding neighbors. These Outliers should not be contained in any cluster and should be discarded during the mining process. Identification of outliers in spatial data has attracted significant attention from geographers and data mining experts. They are different from traditional outliers in the following aspects. First, traditional outliers focus on global comparison with the whole data set while spatial outliers pay more attention to local differences among spatial neighborhood. Second, traditional outlier detection mainly deals with numbers, characters, and categories, whereas spatial outlier detection processes more complex spatial data such as points, lines, polygons, and 3D objects. Third, to detect spatial outliers, spatial correlation need be considered. As described by the geological rule of thumb, “Everything is related to everything else, but nearby things are more related than distant things [1].” Spatial outliers can be classified into two types of noise background noise and chains. The background noise is some isolated points which often distribute randomly in the database; the chains are formed of noises which connect two separated clusters. Wave atoms are a recent addition to the collection of mathematical transforms for harmonic computational analysis. Wave atoms are a variant of 2D wavelet packets that retain an isotropic aspect ratio. Wave atoms have a sharp frequency localization that cannot be achieved using a filter bank based on wavelet packets and offer a significantly sparser expansion for oscillatory functions than wavelets, curvelets and Gabor atoms. Wave atoms capture coherence of pattern across and along oscillations whereas curvelets capture coherence only along oscillations. Wave atoms precisely interpolate between Gabor atoms [2] (constant support) and directional wavelets [3] (wavelength ~ diameter) in the sense that the period of oscillations of each wave packet. (wavelength) related to the size of essential support by the parabolic scaling i.e. wavelength ~ (diameter)2 Section 2 Introduce the motivation behind using wave atom techniques for clustering large spatial databases. Section 3 is a brief introduction on Wave atom transformation. Section 4 discusses our clustering method,  Wave  Atom Cluster and analyzes its complexity. Section 5 show the experimental evaluation of the effectiveness and efficiency of our approach using very large data sets as illustrated. Finally in Section 6, concluding remarks are offered.

• II.    Related Work

  There are many techniques that can be used in clustering process like partitioning, hierarchical, density based and grid based techniques. One of the most important problems is the linearly proportional of clustering algorithms computational complexity to the size of the data set. Grid based approaches are popular for mining clusters in a large multidimensional space wherein clusters are regarded as denser regions than their surroundings. The great advantage of grid-based clustering is its significant reduction of the computational complexity, especially for clustering very large data sets. Grid clustering is concerned not with the data points but with the value space that surrounds the data points[4]. Wang et al. (1997) [5] proposed a STatistical INformation Grid-based clustering method (STING) to cluster spatial databases, algorithm captures statistical information associated with spatial cells in such a manner that whole classes of queries and clustering problems can be answered without recourse to the individual objects. Another grid based algorithm is Grid-based Density-Isoline Clustering (GDILC)[6], the idea of this algorithm is that the density-isoline figure depicts the distribution of data samples very well,grid-based method will calculate the density of each data sample, and find relatively dense regions, which are just clusters. GDILC was capable of eliminating outliers and finding clusters of various shape

An adaptive spatial clustering algorithm based on delaunay triangulation [7] introduce an algorithm that employs both statistical features of the edges of Delaunay triangulation and a novel spatial proximity definition based upon Delaunay triangulation to detect spatial clusters. Algorithm can automatically discover clusters of complicated shapes, and non-homogeneous densities in a spatial database, without the need to set parameters or prior knowledge. The user can also modify the parameter to fit with special applications. Wave Cluster is a novel multi-resolution clustering approach based on wavelet transforms[8]. it can effectively identify arbitrary shape clusters with complex structures such as concave or nested clusters at different degrees of accuracy or scales. A lot of studies has been done using wavelet technique to cluster dataset like using Wavelet Packet Decomposition in clustering[8], In few years ago Wave atom was presented by Demanety and Ying [10] ,it depends on multiscale transforms for image processing and numerical analysis. Wave atoms come either as an orthonormal basis or a tight frame of directional wave packets. They also provide a sparse representation of wave equations, hence the name wave atoms .Our scope in this paper is to implement the idea of wave atom in grid based clustering techniques as will seen in next sections.

• III.    Wave Atom-Based Clusterin

• A.    Wave Atom Transform

We can say that classical wavelet transform, pass from one stage to another, only the approximation will decomposed. In other hand the decomposition in wavelets packets could be pursued into the other sets, which is not optimal. So we can say that the optimality is related to the maximum energy of the decomposition. The idea is then to looking for the path yielding to the maximum energy through the different subbands. Wave atom is multiscale transforms for image and numerical analysis. We can define some fundamentals notions following [10].

Let us define 2D Fourier transform as:

̂(ԝ)=∫е f(x)dx                (1) [11]

f ( X )=(  ) ∫ _eixw ̂(W) dw            (2) [12]

Wave atoms are noted as, with subscript. The indexes are integer-valued associated to a point in the phasespace defined as follows:

xμ= 2 jn , ԝμ= π2im, C!2j ≤max , |mi|≤ С22] In [10], they suggest that two parameters are sufficient to index α lot of known wave packet architectures. The index indicates whether the decomposition is multi scale (β = 1) or not (α= 0) ; and β indicates whether basis elements are localized and poorly directional (β = 1) or, on the contrary, extended and fully directional (α= 0).We think that the description in terms of α and β will clarify the connections between various transforms of modern harmonic analysis. Wavelets (including Multi Resolution Analysis, directional and complex) correspond to α = β = 1 , for ridgelets [β] α= 1, β = 0 , Gabor transform α = β = 0 and curvelets correspond to α = β = 1/2. Wave atoms are defined for α = β = 1/2 . Figure 1 illustrates classification. In order to introduce the wave atom, let us first consider the 1D case. In practice, wave atoms are constructed from tensor products of adequately chosen 1D wavelet packets. An one-dimensional family of real-valued wave packets ψ, (x),ј≥0,m≥0,n∈Ζ , centered in frequency around ±ԝ , =±π22 m with С ^2 j ≤m≤С22 j ; and centered in space around x ,= 2 J n , is constructed. The one-dimensional version of the parabolic scaling inform that the support of ψ , (ԝ) be of length 0(22j ) , while ԝ , (ԝ) = 0(2, 2j) [9]. The desired corresponding tiling of frequency is illustrated at the bottom of Figure 2. Filter bank-based wavelet packets is considered as a potential definition of an orthonormal basis satisfying these localization properties. The wavelet packet tree, defining the partitioning of the frequency axis in lD, can be chosen to have depth j when the frequency is 2 2j , as illustrated in Figure 2. Figure 2 presents the wavelet packet tree corresponding to wave atoms. More details on wavelet packet trees can be found in [2]. The bottom graph depicts Villemoes wavelet packets on the positive frequency axis. The dot under the axis indicates a frequency where a change of scale occurs. The labels "LH", respectively "RH" indicate a left-handed, respectively right- handed window [10]. In 20 domain, the construction presented above can be modified to suit certain applications in image processing or numerical analysis: The orthobasis variant [9]. In practice, one may want to work with the original orthonormal basis φ Ц (x) instead of a tight frame. Since φ Ц(x)=φц (x) + φ ц (x) each basis function φ Ц (x) oscillates in two distinct directions, instead of one. This is called the orthobasis variant.

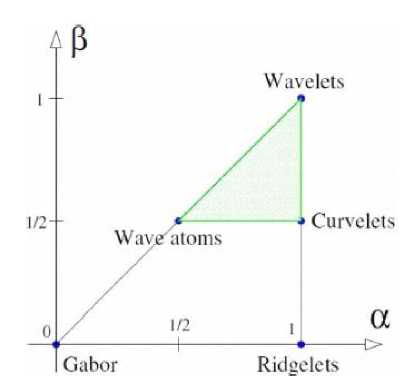
Fig.1 Classification of α and β for Wavelets ,Curvelet and Wave atoms

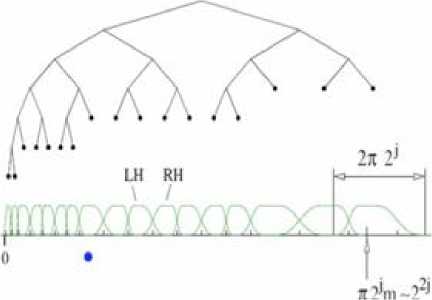
Fig.2 wavelet packet tree corresponding to wave atoms

• B.    Multi-Resolution Analysis

  As we all know, wavelet and wave atom transform is a kind of signal processing technique that decomposes a signal into different frequency subbands. They are a types of signal representation that can give the frequency content of the signal at a particular instant of time by convolving the filter. [13] they have advantages over traditional Fourier and windowed Fourier methods in analyzing physical situations where the signal contains discontinuities and sharp spikes. When we look at a signal with a small window, we would notice its small features. Analogically, we would get gross features if we look at this signal with a large window. The result in wavelet analysis is to see both the “forest” and the “trees”, However, wavelet transform is referred to so many convolve operations due to the property of multi-resolution analysis that the calculation complexity increases exponentially. The concept of multi-resolution analysis was formally introduced by Mallat [1989] and Meyer [1993]. Multi-resolution analysis provides a convenient framework for developing the analysis and synthesis filters [10].Multi-resolution representations are very effective for analyzing the information. Considering the exellent multi-resolution property of wavelet transform, we apply wavelet transform clustering on after-frame-difference binary images for getting rid of the noises and obtaining arbitrary shape moving objects.

• IV.    Proposed Algorithm

Let us have a set of spatial objects ,1 ≤ і ≤ N , the goal of the algorithm is to detect clusters and assign labels to the objects based on the cluster that they belong to. The main idea in Wave tom Cluster is to transform the original feature space by applying waveatom transform and then we will find the dense regions in the new space. It results sets of clusters at different resolutions, which can be chosen based on users' needs. The main steps of wave-atom Cluster are shown in Algorithm 1.

Algorithm 1

Input: Multidimensional data objects’ feature vectors

Output: clustered objects

• 1.    Quantize feature space, then assign objects to the units.

• 2.    Apply wave atom transform on the feature space.

• 3.    Find the connected components (clusters) in the transformed feature space, at different levels.

• 4.    Assign label to the units.

• 5.    Make the lookup table.

• 6.    Map the objects to the cluster

• 7.    Change number of wave atom coefficient to take other resolution and back to step 2

Each і dimensional of the d-dimensional feature space should be divided into mi intervals; this process is called (Quantize Feature Space), which is the first step of wave atom Clustering algorithm. If we assume that mі is equal to m for all the dimensions, there would be md units in the feature space. Then the objects will be assigned to these units based on their feature values. Let Fk = (f1, f2, . . . , fd) be the feature vector of the object ok in the original feature space. Let Mj = (v1, v2, . . . ,vd) denote a unit in the original feature space where

• vі, 1 ≤ vі ≤ mі, 1 ≤ і ≤ d,

is the location of the unit on the axis Хі of the feature space. Let we have ѕі be the size of each unit in the axis Хі . An object ok with the feature vector Fk = (f1, f2, . . . , fd) will be assignd to the unit Mj = (v1, v2, . . .,vd)

іf ∀ і (vі - 1)ѕі ≤ fі ≤ vіѕі , 1 ≤ і ≤ d

The number (or we can say size) of these units is an important issue that affects the performance of clustering.

The second step in wave atom Cluster algorithm is applying discrete cosine transform on the quantized feature space. wave atom transform will be applied on the units Mj results in a new feature space and so new units Tk . Cosine Cluster detects the connected components in the transformed feature space. Each connected component is a cluster which is a set of units Tk. For each resolution r of cosine transform, there is a set of clusters СТ, but usually number of clusters is less at the coarser resolutions.

In the fourth step of the algorithm, Wave atom Cluster labels the feature space units which are included in a cluster, with its cns , cluster number. That is ∀с ∀ Tk , Tk ∈ с ⟶ lTk = cn , с∈ cr, where lTk is the label of the unit Tk. The clusters which are found cannot be used directly to define the clusters in the original feature space, since they exist in the transformed feature space and are based on wavelet coefficients. Making a lookup table LT is made by the wave-atom cluster to map the transformed feature space units to the units in the original feature space. Waveatom makes a lookup table LT to map the units in the transformed feature space to the units in the original feature space. Each entry in the table specifies the relationship between one unit in the transformed feature space and the corresponding unit(s) of the original feature space. So the label of each unit in the original feature space can be easily determined. Finally, WaveAtom Cluster assigns the label of each unit in the feature space to all the objects whose feature vector is in that unit, and thus the clusters are determined. Formally,

∀ ∀ Mj ,   ∀Oi ∈ Mj ⟶ lOi =   ,c∈ CT,

• 1    ≤ i ≤ N

where tot is the cluster label of object 0 i .

• V. Performance Evaluation

We are going to evaluate the performance of our proposed clustering algorithm in this section, and we will show its affectivity. Tests were done on artificial dataset and also on datasets used to evaluate Cosine based clustering [13]. We mainly compare our clustering results with wavelet clustering algorithm.

a) DS1

b) DS2

c) DS3                        d) DS4

c) DS5

Fig.3 Datasets

Table1: Results of applying wave atom on DS2 with

No of coefficients

DS1

DS2

DS4

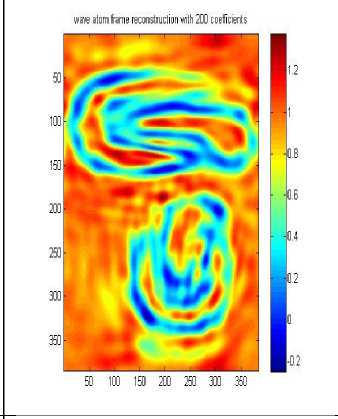
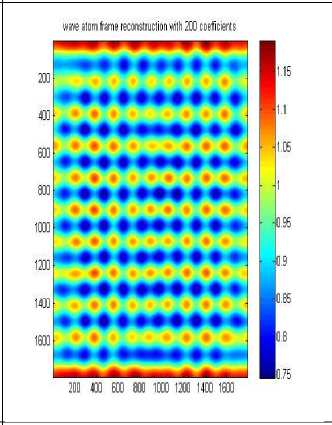
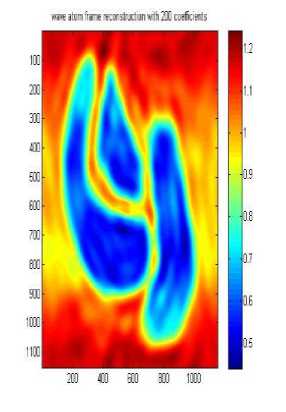
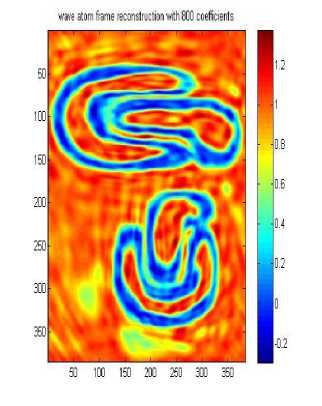
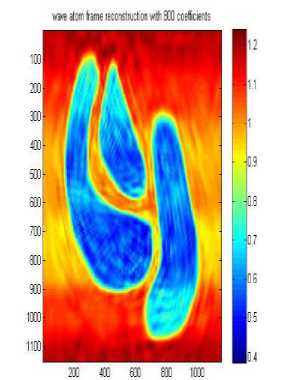
wave atom frame reconstruction with 800 coefficients

™ Ve ♦ • e•e•e•

11.15

♦ i ♦ м e 11 e •

e t н ♦ i e i e <

иннееее

емие» • м

# * n ♦ Ф

200 400 600 800 1000 1200 1400 1800

■0.95

■0.9

i0.85

0.8

0.75

0.7

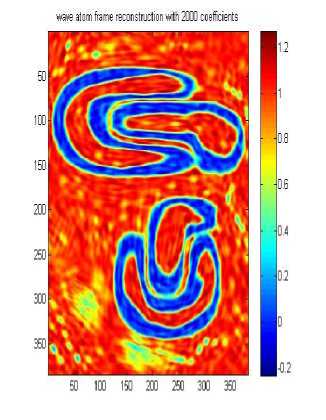
wave atom frame reconstruction with 2000 coefficients

I wwwwevwe » * ♦ ♦ f н ♦ । * |

I ** ♦ * * * * if»-» ■■ t ♦ ♦ t * t * * f e J

«■ e * * t * ♦ t * tj А***ЛЛ* e t ♦ t ♦* ♦ * •

* ** ♦-♦ * 4 ♦ 11 н t • * e * j

I • м • • * * * fj 1 ф.* # ♦ *■* * w* «»#»<♦»»«»] > ^n****^ ■*♦* e • e ♦'*•#»# * i . ♦ W « * * V » A * 4 * » » 4 * 4 * * * "* w f                            .

*»'•**•••* I

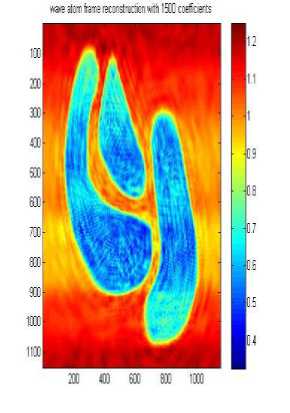
Д

• A. Wave atom clustering coefficients

In our approach we use Synthetic Datasets which contain noise and irregular shape as shown in

Fig.3 .Dataset DS1 is 2-dimensional feature space, where the two dimensional data points have formed four clusters, it is the same that used in [14], the visualizations of the 2-dimensional feature spaces and each point in the images represents he feature values of one object in the spatial datasets. Each row or column can be considered as a one-dimensional signal, so the whole feature space will be a 2-dimensional signal. Boundaries and edges of the clusters constitute the high frequency parts of this 2-dimensional signal, whereas the clusters themselves, correspond to the parts of the signal which have low frequency with high amplitude. When the number of objects is high, we can apply signal processing techniques to find the high frequency and low frequency parts of n-dimensional signal representing the feature space, resulting in detecting the clusters. Datasets DS2 and DS3 are the same as used by [14]. They are shown in Figure 3 b and c. Each dataset consists of 100,000 points. The points in DS3 are randomly distributed while DS2 and DS3 are distributed in a grid and sine curve pattern respectively. The other datasets shown in Figure 3 were generated as in [14]. Data set DS4 is the noisy version of DS5 that is generated by scattering 1000 noise points on the original dataset, As shown the datasets above contain 3 arbitrary shaped clusters. They contain also nested or concave clusters with outlier and noisy shapes.

B. Wave atom clustering coefficients

We apply our algorithm to different datasets and each time we try to apply it with changing the number of coefficients as shown in Table 1, below. It is clear that increasing the number of wave atom transformation coefficients will propositionally increase the accuracy of clusters but more increasing will may consider noise and outlier clusters .The time of transformation will be increased also but it is shown that results will be good and efficient in 800 and 2000 coefficients and there are some lose in 200 coefficients.

in wave cluster algorithm and compare output result with result from changing number of coefficient of wave atom 200, 800, 1500, 2000 respectively. Table 2 compare the time consuming of using Wave cluster and Wave atom clustering in term of second. There difference in time consuming because wave atom has O(N logN) and wave cluster has O(N) but they different in term of accuracy.

Original Dataset Approximation A1 Approximation A2 Approximation A3

50010001500     50010001500

Approximation A4 Approximation A5

Approximation A7

500 10001500

Approximation A6 Approximation A7

50010001500       50010001500

Fig.4 Wavelet Clustering on DS4

Table 2 Results of applying wave atom and wavelet clustering on different datasets

Algorithm	Time (sec)	Time (sec)	Time (sec)
	DS-4	DS-6	DS-5
Wave cluster	0.686593	10.229812	19.603167
Wave atom Clustering	5.042399	14.624251	27.363233

• C. Wave atom clustering vs. wavelet clustering

In order to measure the performance of our algorithm we should compare it with other algorithms like wavelet clustering or BIRCH algorithm [14], but because of similarity between our algorithm and wavelet clustering algorithm we decide to apply comparison between these two algorithms.

Properties of testing Environment, Processor – Intel® Core(TM) i3 CPU M380 @ 2.53GHZ ,RAM – 4.00 GB (2.92 GB usable) and System Type – 32-bit Operating System After applying cluster algorithm based on wavelet we found that increasing the number of approximation will cause big lose in cluster shape as shown in Figure 4 below, this is a known problem in wavelet transform which is called multi-resolution problem which is solved in our proposed algorithm as shown in Table 2. Finally we evaluate the performance of Wave atom clustering and demonstrate its effectiveness on different types of distributions of data. We mainly compare our clustering results with wave cluster. We compare output result of using 5 resolutions

• VI. Conclusion

In this paper, the Wave Atom Clustering approach is presented. We apply wave atom transform on the spatial data feature space which helps in detecting arbitrary shape clusters at different scales with more accurate results than other transformation. It is a very efficient method with time complexity of O(N logN), where N is the number of objects in the database, so it will be more attractive for large datasets. Wave atom clustering takes more time but it gives more accurate results,it is insensitive to the order of input data to be processed. Moreover, it is not affected by the outliers and can handle with better results than Wave Cluster algorithm.

Acknowledgment

The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments.