Database Semantic Interoperability based on Information Flow Theory and Formal Concept Analysis

Published Online July 2012 in MECS

In this research, we try to apply IF and FCA theories to achieve database semantic interoperability. Interoperability is the ability of two systems to exchange information, and correctly interpret and process this information [1]. In our view, the essential aim of semantic interoperability is to alleviate the difficulties in interoperability caused by semantic heterogeneities.

As commerce and computer science are developing rapidly, databases become more widely used and translating data between multiple heterogeneous, autonomous, distributed databases becomes a growing need, so database interoperability and integration are long standing open problems with extensive research literature. There are many different frameworks for database integration, which can be classified into three main approaches: (1) Global schema approach [2] defines a global schema over the component database systems that capture the union of the ‘information' content of the component schemas; (2) Federated database approach [3] which exports schemas of distributed database and integrates with the local schema to provide the necessary views for the local users; and (3) Multidatabase language approach [1]provides powerful multidatabase languages for querying a group of non-integrated schemas. All of the above approaches rely on some integrated or import/export schema. However, they do not address the resolution of heterogeneous data conflicts to build such a schema.

Schema matching is pursued from the early stage of integration. Doan and Halevy [4] classify it into two main categories, i.e., rule-based and learning-based solutions. Rule-based schema matching employs manual matching rules to explore ‘information’ associated with schema, for instances, types, structures and constraints. Although a rule-based solution is inexpensive and operationally fast, it has the main drawback that it is unable to capture the requisite, operational ‘information’ associated with data instances and this aspect is significant for contemporary, integrated systems. Many learning-based solutions have been developed and they have considered a variety of learning techniques and exploited both schema and data information. For example, the SemInt system [5] uses a neural network learning approach. It matches schema elements based on attribute specifications (e.g., data types, scale, and the existence of constraints) and statistics of data content (e.g., maximum, minimum, average, and variance). This approach exploits data instances effectively. These instances can encode a wealth of information that greatly reduces the matching process. Learning methods can exploit previous matching efforts to assist in the current ones [6]. Compared with rules-based techniques the main drawback of learning methods is that they require training.

The history of data matching is quite similar to schema matching, i.e., from manual rule-based to learning-based approaches. A number of researchers have followed this line, for example, Hernandez and Stolfo [7] put forward manually specified rules whilst others use learning-based rules [8][9].

After reviewing the above literature, we find that much of the work in the context of database integration and interoperability focuses on setting up semantic matches based on clues in the schema and data. However, semantics are embedded in four places: the database model, conceptual schema, application programs and minds of users’ [10]. We can see that most semantic integration procedures can only make use of information contained in the first two, so there is still a general problem, which is the resolution of semantic level heterogeneity.

In finding an innovative approach to addressing aforementioned gap in knowledge, we notice that M. Schorlemmer and Y. Kalfoglou [11] proposed a mathematically sound application of information flow theory to enable semantic interoperability of separate ontologies that represent a similar domain. They tackle the problem of semantic heterogeneity from a theoretical standpoint with attainable, practical applications in a variety of knowledge sharing structures, including ontologies. We adopt their approach in tackling databases, and we find that using IF and FCA does seem to enable a new and interesting approach to database alignment.

The remainder of this paper is organized as follows: Section 2 gives a briefly review of basic theoretical tools. Section 3 describes the architecture for achieving semantic interoperability between databases. Section 4 presents a case study to explain what problems are solved and what new problems are raised. Conclusion and future work are given in the final section.

• II.    Basic Theoretical ToolsA.    Channel–theoretic Information Flow (IF)

Information Flow Channel (IF) is a modern theory of semantic information and information flow put forward by Barwise and Seligman [12]. Information Flow is possible due to the regularities among normally disparate components of a distributed system. The basic notions of IF (See Terminology) have been applied to explore semantic information and knowledge mapping and exchanging. Kent [13][14] achieves semantic integration between ontologies based on an IF approach. Then, based on IF, an ontology mapping method has been developed in the field of knowledge sharing and cooperation by Kalfoglou and Schorlemer [15]. They also construct an application of IF to solve problems of semantic interoperability between ontologies [11][16]. A good example is cited in [11], which shows how the Information Flow theory enables semantic interoperability. We describe this example briefly here. UK and US governments have ministries, which are named differently, but these ministries may common responsibilities. For example, in Figure 1, we find that PA and BCA have the same responsibility – passport services, IND and INS have the same responsibility – immigration control, and EUBD and BEA have the same responsibility – promote productive relations. All of the above are partial alignments, which we find through domain knowledge. So what is the relationship between two governments’ ministries, or in other words how may we align them? After using the information flow theory to model and analyze the situation, some constraints are identified such as FCO ├ DoS. The constraint FCO ├ DoS means that as far as the a few pairs of responsibilities go, which are identified at the beginning of the modeling and analysis by using domain knowledge, if a responsibility belongs to UK Foreign and Commonwealth Office, then it must be the case that a corresponding responsibility belongs to US Department of State. But converse is not true. That is to say, constraints capture the alignment between the ministries.

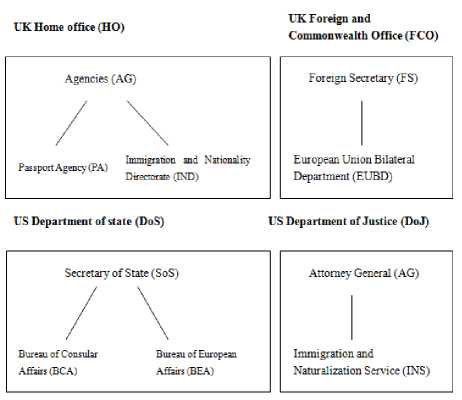
Figure 1: Hierarchical structures of government ministries

• B.    Formal concept analysis (FCA)

FCA was developed by Rudolf Wille [17] as a method for data analysis, information management, and knowledge representation [18]. The basic notions of FCA are shown in terminology. FCA not only provides solid mathematical foundations for information and knowledge retrieval [19][20], but also provides concept lattice [17][21][22] for respective representations along with concept graphs [23]. Based on FCA, Conceptual Knowledge Discovery in Databases (CKDD) has been developed by Gerd stumme, Rudolf wille and Uta wille [24]. The CKDD aims to support a human – centered process of discovering knowledge from data by visualizing and analyzing the formal conceptual structure of the data. In this paper CKDD is the key for applying IF in database semantic interoperability. FCA is also supplementary to IF in data modeling.

• III.    Architecture for Achieving Semantic Interoperability between Databases

Figure 2 illustrates the architecture of a system for achieving semantic interoperability between two databases. Firstly, a process of Conceptual Knowledge

Discovery in Databases (CKDD) is carried out using TUPLEWARE. In order for two systems to be considered semantically integrated, both will need to commit to a shared conceptualization of the application domain [16]. CKDD is a right way for the conceptualization of two autonomous databases. Secondly, the knowledge from the databases will be formulated as IF classification , which are then connected through infomorphisms such that an IF channel that represents the databases involved in the alignment is created. This channel enables the identification of constraints, which capture the alignment as said earlier.

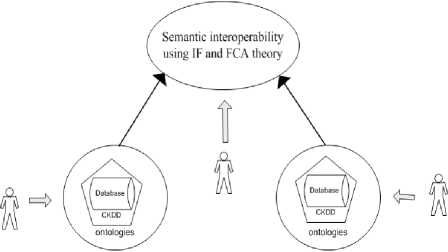
Figure 2: Architecture of semantic interoperability between databases

• IV.    Case Study

In this section, a case study is described with which we show the stages of our method outline above. Then we explain what problems are solved and what new problems are raised.

• A.    The Scenario

Let us assume that two international companies namely A and B want to cooperate and they respectively have an autonomous database. The two databases are shown in Figure 3 and Figure 4. The staff of both companies is distributed in many different cities in the world, and it is required that staff belonging to different companies work together. The precondition is that they must work in the same city or country. In this situation, how can we achieve database semantic interoperability so that we would enable the two companies’ managers to obtain information from the two heterogeneous, autonomous and distributed data sources?

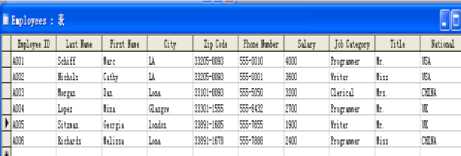
Figure 3: Database 1 from company A

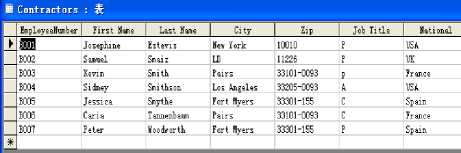
Figure 4: Database 2 from company B

• B.    Conceptual Knowledge Discovery in Databases

With our architecture shown above, we carry out conceptual knowledge discovery from the two databases using FCA first. Let us explain why we do this first. Semantic interoperability is possible only because the requester and the provider have a common understanding of the “meanings” of the requested services and data. As already mentioned, in the literature two kinds of methods are said to have been used for achieving data and schema match, namely rule based and learning based solutions. These methods can find matches based on either the character of the data or the rules on how data may change, but they are not full semantic matches in terms of what the data refers to in the real world. Moreover, such a common understanding could be superficial. For example, I want to buy a football and I tell the shop assistant that I want something that is round and can be kicked about. But I might be given a small balloon. The cause of such a problem seems lying with the lack of knowledge of a sufficient level or the lack of adequate expression of the knowledge. To remedy this problem, we start with human - centered knowledge discovery from databases, which would enable the process of identifying semantic interoperability on the knowledge level in place of some syntactic or statistics level. The term of ‘human-cantered knowledge discovery’ refers to the constitutive character of human interpretation that is involved in a process of discovering knowledge from data, and stresses the complex, interactive process of knowledge discovery as being led by human thought [24]. That is to say, we establish understanding between two different databases against the same background knowledge of users. This would enable the user to know, for example, that the element ‘LA’ from database 1 means Los Angeles, which is part of user’s background knowledge. Likewise, the element ‘Los Angeles’ from database 2 also means Los Angeles in the user’s background knowledge. Thus, ‘LA’ from database 1 has the same meaning as ‘Los Angeles’ from database 2. If we used a rule based method based on syntactical characteristics, and a rule could be: if the first letters of two words that make up a location are the same respectively, then the two locations are the same. With such a rule, ‘LA’ and ‘Los Angeles’ match. But ‘Latin American’ and ‘Los Angeles’ also match. That is to say, tapping users’ background knowledge if it is available provides us with a simpler and yet effective means of aligning databases. Now the question is how to first of all reveal relevant background knowledge. We find FCA is a useful intellectual tool for this.

As said earlier, FCA has led to some software systems such as TOSCANA and TUPLEWARE, which could be used as a tool for discovering knowledge in databases. In this case study TUPLEWARE is used.

With TUPLEWARE after database connection, we select data in which we are interested by using SQL query statements. We will neither select all data nor try and discover all knowledge in terms of formal concepts from a database, as not all are relevant to our purposes. In our scenario, we only select the data relevant to the requirement, i.e., working in the same city or country. Such an approach is called human–centered knowledge discovery in the literature [24]. It seems more manageable and relevant than other approaches. For our case, we analyze the scenario and find that:

• •    There are members of staff working for company A and company B respectively.

• •    If we find members of staff of company A and members of staff of company B working in the same city or country, then we know that they can communicate with each other and work together.

From this information we know that the data that are to be selected must be concerned with staff and where they are working. To get the information, we use the SQL statement: “select EmployeeID, City, National from Employees”.

The next step is to identify formal objects from the data that has been selected from the database. The requirement enables us to identify what these formal object sets are. We know that Interoperability is the ability of two systems to exchange information, and correctly interpret and process this information [1]. We take the view that what we want to exchange with one another are formal objects. In this case, we choose “EmplyeeID” as the object set, because what we want to know is who of the staff of company A can work together with staff from company B. Thus we obtain an one- and many–valued formal context (See Figure 5).

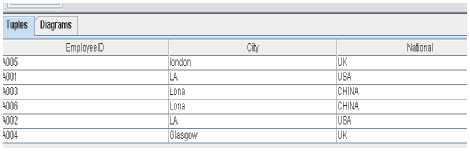
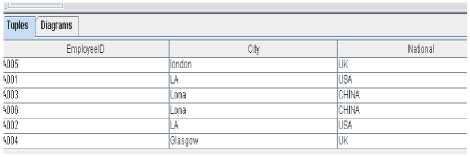
Figure 5: A one- and many –valued context

The second step of the conceptualization with FCA is concerned with categorization. To meet the requirements we select ‘city’ as the formal attribute set from the tuple (Figure 5). This is a very important character of human centered knowledge discovery in databases as this can make the knowledge discovery more pertinent to the needs of the user. Then a formal context can be constructed (Figure 6).

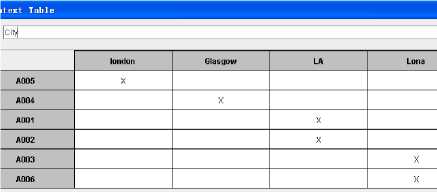
Figure 6: a Formal context about ‘City’ from database 1

With this formal context, concept lattice can be derived as shown in Figure 7. There are several nodes in the concepts lattice and every node represents a formal concept. For example, the node on the right side of Figure 7 represents the formal concept with the extension ‘A001, A002’ and the intension as the singleelement set ‘LA’.

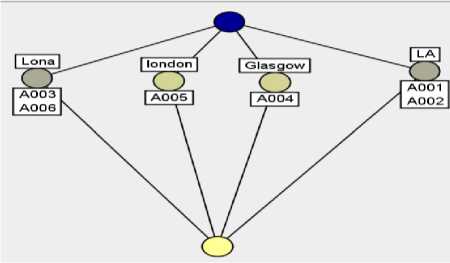
Figure 7: the concepts lattice corresponding with formal context about ‘City’.

In the same way we can select ‘national’ as the attribute set, and then derive a context and corresponding concept lattice as shown in Figure 8 and Figure 9.

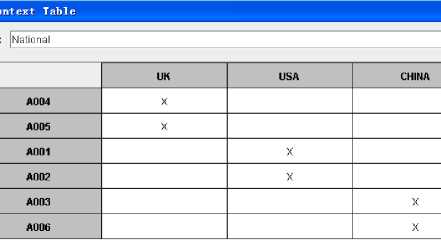
Figure 8: A Formal context about ‘National’ from database 1

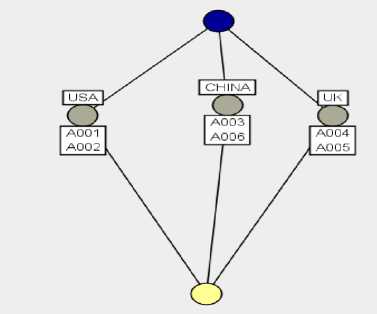
Figure 9: The concepts lattice corresponding with formal context about ‘National’ from database 1

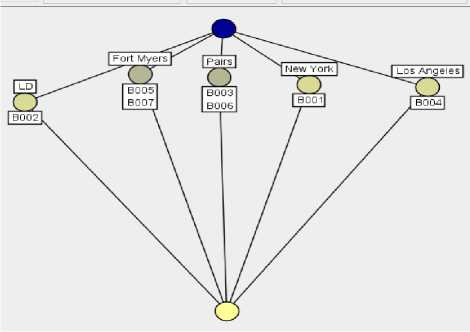
Figure 11: the concepts lattice corresponding with formal context about ‘City’ from database 2.

Thus, using the TUPLEWARE system, a conceptual data system has been set up. A conceptual data system consists of a database and a collection of formal contexts, called conceptual scales , together with line diagrams of their concept lattices [24]. From database 1, the two contexts and their corresponding concepts lattices have been constructed to form a conceptual data system.

Now we can get the knowledge we want from a database by examining its conceptual data system. For instance, there is a node on the right hand side of Figure 6, which represents the formal concept with the extension ‘A001, A002’ and the intension ‘LA’. ‘A001’ is an employee ID, which tells us that there is a person who works for company A. ‘LA’ means Los Angeles. From this formal concept, we obtain the knowledge that there are two people working for company A in Los Angeles and their employee ID are respectively ‘A001’ and ‘A002’. This way, we can translate every formal concept into text regarding who works for company A and where.

We can carry out knowledge discovery from database 2 in the same way, which gives us a conceptual data system that consists of database 2 and two formal contexts together with their corresponding concepts lattices (See Figures 10, 11, 12 and 13).

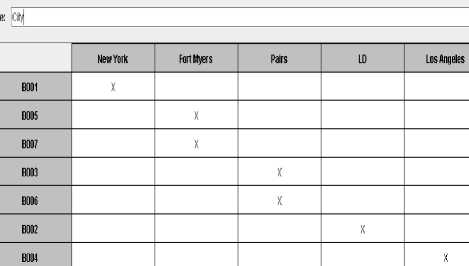
Figure 10: a Formal context about ‘City’ from database 2.

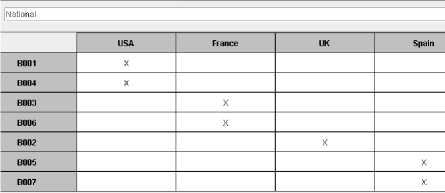
Figure 12: a Formal context about ‘Nations’ from database 2

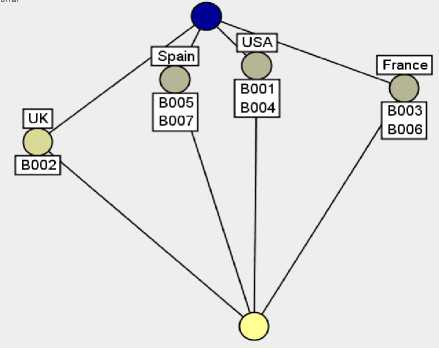
Figure 13: the concepts lattice corresponding with formal context about ‘Nations’ from database 2

From this conceptual data system the knowledge about who works for company B and where is discovered. Up to this point, we have completed the knowledge discovery from two different databases. The next step is to identify semantic alignment.

• C.    Achieving Semantic Alignment between Databases Constructs

Following Schorlemmer and Kalfoglou’s [11], we take four steps to identify semantic alignments between two conceptual data systems as shown below:

• 1.    Define IF classifications  for the formal

• 2.    Construct an IF channel – its core and

• 3 .Identify an IF local logic on the core of the IF channel, which captures the working of the channel.

• 4 . Distribute the IF local logic on the core to the sum of the IF classifications that model the databases whereby to obtain the IF theory that formulates the desired alignment between data constructs.

contexts of the conceptual data system described above.

infomorphisms that connect the IF classifications.

Firstly, we translate various formal contexts that have been arrived at into IF classifications. We mentioned earlier that using the TUPLEWARE system two conceptual data systems were set up. With the same TUPLEWARE system contexts can also be combined together. From the two conceptual data systems that have been constructed by using TUPLEWARE we can define two contexts as shown below:

	London	Glasgow	LA	Lona	USA	UK	CHINA
A001			x		X
A002			X		X
A003				x			X
A004		X				X
A005	x					X
A006				x			X

Figure 14: the contexts (classification) S from database 1

	LD	Fort	Pairs	York	Angeles	USA	France	UK	Spain
B001
B002	X
B003			X				X
B004					x	X
BOOS		X							X
B006			X				x
BOOT		X							X

Figure 15: the contexts (classification) T from database 2

Secondly, we construct an IF channel by identifying its core and infomorphisms that link the core and component classifications. Through observing the two contexts, we find some partial alignments based on the found common knowledge, which are:

London1 LD2

LA1    Los Angeles2

USA1   USA2

UK1   UK2

(‘1’ indicates elements from database 1, and ‘2’ database 2)

The above partial alignment is a binary relation between typ(S ) and typ(T). In order to model this alignment as a distributed IF system, two total functions g 5 and g ⁵ from a common domain typ(A) = {a, b, c, d} are used to represent this binary relation. For example, the alignment London1 О LD2 can modelled as g 5 (a) = Londonl and g ⁵ (a) = LD2. This will constitute the type-level of couple of infomorphisms.

S ^—- A -——> T

5      5

Figure 16: the functions g and g from typ(A)

g 5 (a) = Londonl	gr(a) = LD2
g;(b)=LAl	g r(b) = Los Angeles2
gs(c) = USAl	gr(c) = USA2
g'(d) = UKl	gr(d) = UK2

Figure 17: type-level infomorphisms

	a	b	c	d
nl	x
n2		X
n3			X
n4	x	X
n5	X		X
n6		X	X
n7	X	X	X
n.8	X			X
n.9		X		X
nlO			X	X
nil	X	X		X
nl2	X		X	X
nl3		X	X	X
nl4	X	X	X	X
nl5				X

Figure 18: the classification A

To satisfy the fundamental property of infomorphisms (See the notion of inforphisms), the token level of g and g must be as follows:

g^(A001) = n6;	gr(B001) = n3;
g'(A002) = n6;	gr(B002) = n8:
gs(A004) = nl5;	gr(B004) = n6:
gs(A005) = n8;

Figure 19: token-level infomorphisms

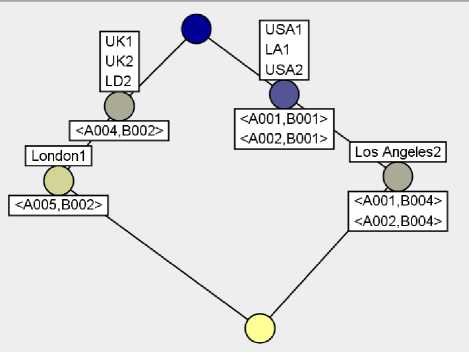
Figure 22: the concepts lattice of the core

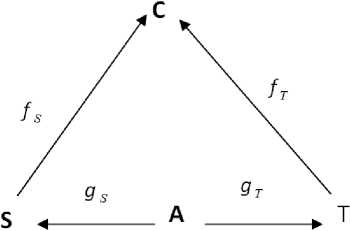
Figure 20: Distributed system

There are natural infomorphisms fs and fT that connect S and T with C respectively. The classification C is the core of the channel and it is constructed such that the types are from typ(S) and typ(T) that have taken part in the infomorphisms fs and fy and the tokens are pairs of tokens determined by the alignment infomorphisms 9 s and 9т . for example, the core C will have the token < A001 , B001 > , because g ^∨ ( A001 ) = n6 and g ^∨ (B001) = n3 , and both n6 and n3 are of type c in A .

A fragment of C is showed as follows:

	UKI	USA1	London1	LAI	UK2	USA2	LD2	Los Angeles2
		X		X		X
		X		X		X		X
		X		X		X
		X		X		X		x
	X				X		X
	X		x		X		X

Figure 21: the IF channel classification on the core

From the core C we identify constraints on the core as shown below.

London1 ├ LD2;

London1 ├ UK2;

Los Angeles2 ├ LA1;

USA2 ├ LA1;

LA1 ├ USA2;

UK1 ├ LD2;

UK1 ├ UK2;

LD2 ├ UK1;

UK2 ├ UK1;

Los Angeles2 ├ USA1;

USA2 ├ USA1;

USA1 ├ USA2;

The constraints show that as far as those pairs such as go, how some of the columns (i.e., attribute s of relation s) of two tables may be aligned. For example, London1├ LD2 means that if London1 covers (due to A005 working in

London1), which it does, then LD2 also covers (due to B002 working in LD2).

Finally, we distribute the IF logic to the sum of the community IF classifications to obtain the IF theory that describes the desired semantic interoperability. The constraints that capture the semantic interoperability are found to be:

{A004, A005} ├ {B002};

{B002} ├ {A004, A005};

{A005} ├ {B002};

{A001, A002} ├ {B001, B004};

{B001, B004} ├ {A001, A002};

{B004}├ {A001, A002}.

Note that these constraints are concerned with certain relationships between groups of staff in terms whether they have members that are working at those known corresponding locations. For example, {A004, A005}├ {B002} means that for the group that is made up of members of staff A004 and A005 has at least one member, who could be A004 or A005 or both, that works with the member of staff B002 (who happens to be the sole member of the group (B002) at the same location (this is because two corresponding locations happen to be seen as the same location in our case study).

This is the main part of the semantic interoperability between two databases that we have achieved thus far. What could the achieved semantic interoperability tell us? For example, the company A’s manager wants to know all those groups of staff that has at least one member that works at one of those known same locations as at least one member of another group that has a member A004. It could be difficult to get a correct answer to such an intricate question by using a simple SQL statement to query two heterogeneous data sources. But it would be easy to find an answer by using our system given the identified semantic interoperability. Because A004 belongs to the set {A004, A005} and there is a constraint {A004, A005} ├ {B002}, we find that the group of staff whose sole member is B002 from company B is such a group. Furthermore {A004, A005} ├ {B002} also means that as far as those people that work in those known corresponding locations are concerned if one of a pair belongs to the group of people (A004, A005) then that the other of the pair must belong to the group of people (B002). For example, we know that are a pair of such people. As A004 belongs to the group of people (A004, A005) (i.e., satisfies {A004, A005}), B002 must belong to the group of people (B002) (i.e., satisfies {B002}), which he/she obviously does. This may be seen straightforward. But we could define the original semantic correspondences and group the data as we wish to suit our needs of modeling for desired semantic interoperability, the use of the proposed approach presented here could be sophisticated.

The reader may still have doubt about why we use the Information Flow theory. Let us use a simple example to answer this question. Through knowledge discovery in databases, we obtained some original correspondences (in the sense that they form a starting point of the aligning process) between data values from two databases such as ‘London1     LD2’. ‘London1

LD2’ means that ‘London’ from database 1 and ‘LD’ from database 2 have a same meaning – it is a city namely London. Then we may query respective databases to find out who work in London. For example, employee ‘B002’ from company B works together with employee ‘A005’ from company A. It is not a wrong answer, but it is incomplete because ‘B002’ from company B also works together ‘A004’ from company A. In our system, we have a constraint {B002}  ├

{A004, A005}, which shows that either ‘A004’ or ‘A005’ or both satisfies the condition of working together with ‘B002’. That is to say, constrains describe how different types (or groups of tokens) from two different communities are logically related to each other. We achieve this by using the IF theory, and compared with those methods described earlier, Information Flow (IF) does seem to enable us to capture and represent semantic interoperability between any data constructs in terms of levels (e.g., types or data values) and granularity (e.g., single or collections of types or data values) that may be of interest.

• V.    Conclusions

In this paper, we have described a prototype, which was developed based on the theories of IF and FCA. We have shown that our method helps achieve semantic interoperability between databases, and it was tested and verified by using our prototype and TUPLEWARE. Our main findings are the following. First of all, using human–centered knowledge discovery in databases can make the process and the result of achieving semantic interoperability pertinent to particular needs and it is flexible. Secondly setting up common understanding between the requester and the provider using common knowledge makes the semantic interoperability arrived at reliable and veracious. Finally, the IF theory is an advanced theory, which enables capturing and formulating semantic interoperability with mathematical rigor systematically.