Датчик расхода жидкости на основе термоанемометрического микросенсора потока

Корректное измерение количества перемещаемой жидкости в системе, несомненно, представляет как практический, так и теоретический интерес. В теоретическом аспекте интерес прежде всего заключается в верификации разработанных физических моделей, тогда как практическое применение это — определение расхода воды в системах водоснабжения и охлаждения, регулирование течения технологических жидкостей, оценка количества переливаемого бензина на заправочных станциях и др. Датчики расхода жидкости широко используются в машиностроении, энергетике, транспорте, торговле, жилищно-коммунальном хозяйстве, медицине, горном деле, строительстве.

Современной промышленностью выпускается достаточно много видов датчиков расхода жидкости, основанных на различных физических принципах измерения [1]. Датчики расхода на основе сенсора потока теплового типа [2] выделяются среди датчиков, основанных на других принципах измерения, рядом преимуществ, среди которых основные:

– высокая чувствительность;

– низкий уровень дрейфа выходного сигнала;

– отсутствие механически подвижных частей;

– высокая точность показаний;

– отсутствие прямого контакта чувствительного элемента с флюидом.

Общий принцип измерения потока сенсорами теплового типа заключается в зависимости интенсивности конвективного переноса тепла от скорости течения флюида. По конкретному принципу измерения сенсоры потока теплового типа можно подразделить на три основных класса: времяпро-летные, термоанемометрические и калориметрические.

В нашей предыдущей работе [3] представлен обзор сенсоров потока теплового типа для измерений расхода жидкости и газа. Основным выводом обзора является тезис, что в настоящее время быстрое развитие методов формирования микро- и наномасштабных поверхностных структур с улучшенными эксплуатационными характеристиками значительно расширяет возможности для разработки новых конструкций сенсоров и область их практического применения. В частности, миниатюризация конструкции улучшает функциональные характеристики датчиков, существенно снижает стоимость их производства и потребляемую электроэнергию.

В основу настоящей работы положен наиболее распространенный термоанемометрический принцип измерения. Такой выбор обусловлен рядом преимуществ, среди которых можно выделить три основных. Во-первых, термоанемометрический принцип предпочтителен для диагностики больших массовых расходов флиюда, такого как жидкость, в отличие от калориметрического принципа, который обычно используют для диагностики газовых потоков. Во-вторых, термоанемометрический принцип измерения достаточно прост для практической реализации. Времяпролетный и калориметрический принципы достаточно требовательны к топологии сенсора. И в-третьих, практическая реализация термоанемометрического принципа измерения обеспечивает необходимые требования по прочности сенсора. Например, калориметрический сенсор, выполненный в виде тонкой мембраны, не выдерживает возможные гидравлические удары в потоке жидкости.

В настоящее время термическая анемометрия один из самых распространенных экспериментальных методов измерения скорости течения и расхода флюида. Существует достаточно большое количество практических реализаций этого мето- да: от проволочных термоанемометров до пленочных [4]. В частности, суть одной из практических реализаций заключается в определении динамики остывания электрически нагретого элемента вследствие процесса теплообмена с жидкостью, который в свою очередь существенным образом зависит от скорости течения жидкости. Так как электрическое сопротивление большинства материалов существенно зависит от температуры, то для определения температуры элемента измеряют его сопротивление.

Действительно, сопротивление резистора R T при температуре T может быть представлено выражением R T = R T [ 1 + a ( T - T 0 ) ] , где a — температурный коэффициент сопротивления (ТКС), R_T — сопротивление резистора при температуре T ₀, соответствующей нормальным климатическим условиям. Таким образом, определив сопротивление резистора, абсолютное значение температуры T резистора можно получить из формулы T = T o + a -¹ ( R T/ R T - 1 ) .

Термоанемометры могут работать в 3 модах: постоянной мощности, постоянной температуры и температурного баланса. Работа в первой из мод основана на нагреве термочувствительного резистора постоянной электрической мощностью и измерении его температуры. Характерное время измерительного процесса в этой моде (время отклика) определяется теплоемкостью материала термочувствительного элемента и интенсивностью теплообмена с окружающей средой.

При работе во второй моде температура термочувствительного резистора поддерживается постоянной, а измеряется подводимая электрическая мощность, необходимая для постоянства температуры. В этой моде термоанемометры работают гораздо быстрее, чем в моде постоянной мощности. Работа в 3-й моде заключается в измерении температуры двух термочувствительных резисторов, расположенных ниже и выше по течению. Величины электрических мощностей, подводимых к каждому резистору для поддержания нулевой разницы температур резисторов, зависят от массового расхода флюида. Благодаря простоте реализации и высокому быстродействию, мода постоянной температуры более предпочтительна для организации измерений, основанных на термоанемометрическом принципе.

Целью настоящей работы является разработка простой, пригодной для инженерных расчетов, аналитической модели термоанемометрического сенсора потока для измерения расхода флюида в канале. Практическая цель работы заключается в разработке и создании датчика расхода жидкости на основе термоанемометрического микросенсора потока.

АНАЛИТИЧЕСКАЯ МОДЕЛЬ

Рассмотрим термочувствительный элемент (резистор) в виде тонкого прямоугольного стержня, расположенного на поверхности цилиндрического канала внутреннего диаметра D , в котором движется жидкость со средней скоростью U . Термочувствительный элемент, имеющий электрическое сопротивление R , нагревается постоянным электрическим током, для чего к его концам приложено напряжение V .

Для расчета температурного поля в твердом теле T = T ( x, y, z, t ) принято использовать уравнение теплопроводности [5], общий вид которого выглядит следующим образом:

d T = a _{v T +} q ⁽ x , y , z , t ) d t  рс        pc

где t — время; ρ , λ , с — плотность, коэффициент теплопроводности и удельная теплоемкость вещества соответственно; q ( x, y, z, t ) — количество тепла, выделяемого или поглощаемого в единицу времени в единице объема.

Рассмотрим работу термочувствительного элемента в моде постоянной температуры, в которой температура элемента поддерживается постоянной, а измеряется подводимая электрическая мощность P = V ²/ R , необходимая для постоянства температуры. Так как на практике обычно определятся среднеинтегральная температура термочувствительного элемента, то нет необходимости подробно рассчитывать температурное поле в элементе. Поэтому будем считать температуру элемента однородной по объему, т. е. не зависящей от координаты, и близкой по значению к среднеинтегральной. В этом случае уравнение теплопроводности существенно упрощается и для термочувствительного элемента в целом выглядит следующим образом:

P - H (U )• 5 •( T - Tw)-Js = 0, (2)

где H — коэффициент теплоотдачи при теплообмене с жидкостью, который зависит от скорости движения жидкости U ; S — площадь контакта термочувствительного элемента с жидкостью; T w — температура жидкости; J s — количества тепла, теряемое элементом в результате теплового контакта с подложкой в единицу времени.

Корректно рассчитать J_s довольно сложно в силу неопределенности теплового контакта между термочувствительным элементом и подложкой. На практике тепловой контакт с подложкой стараются минимизировать, используя при этом современные технологические методы и материалы

[6, 7]. С целью избежать необходимости определения J s целесообразно использовать дифференциальный метод измерения. В этом случае необходимо разработать такую конфигурацию держателя двух термочувствительных элементов, чтобы один элемент находился в потоке жидкости в канале, а второй аналогичный — в практически неподвижной жидкости.

Оба термочувствительных элемента должны обладать максимально приближенными к друг другу теплофизическими характеристиками, тогда в случае одинакового нагрева величина J s для каждого элемента будет одинаковой. Таким образом, записав уравнение (2) для каждого элемента и выполнив вычитание получившихся уравнений, можно получить следующее выражение

AP = P -P2 =[H(U)-H(U = 0)].5•(T-Tw), (3)

где P 1 и P 2 — электрические мощности, подводимые к термочувствительным элементам, находящимся в движущейся и неподвижной жидкости соответственно. Как следует из этого выражения, определив зависимость коэффициента теплоотдачи H от скорости жидкости U , можно рассчитать величину средней скорости жидкости.

Для решения задачи теплообмена в полной постановке с целью определения коэффициента теплоотдачи H необходимо решение уравнений Навье—Стокса, дополненных уравнением переноса энергии. Решение этих уравнений представляет собой достаточно сложную задачу, поэтому для практических расчетов используют методы теории подобия.

Уравнение подобия для процессов теплообмена при вынужденном движении флюида имеет вид Nu = f ( Re; Pr ) , где Nu, Re и Pr — критерии подобия: числа Нуссельта, Рейнольдса и Прандтля соответственно. При обтекании флюидом стержня с однородной температурой, находящегося на поверхности цилиндрического канала диаметром D , критериальное уравнение можно записать в виде системы уравнений для каждого из режимов течения следующем образом [9]:

Nu=

0.664Re2 Pr3 , для ламинарного режима;

(0.037Re⁵ - A )Pr³, для смешанного режима;

0.037Re ^{4 5} Pr ^{1 3}, для турбулентного режима,

где A = 0.037Re C_r - 0.664Re C_r , Re_cr — критическое число Рейнольдса. Критерии подобия в этой системе уравнений запишем как Nu = HL(к_$ ,

Re = UDV f и Pr = v f [a , где X f — коэффициент теплопроводности флюида; ν f — его кинематическая вязкость; a f — коэффициент температуропроводности; L — длина стержня.

Переход от ламинарного к турбулентному режиму течения происходит при достижении критического числа Рейнольдса Re cr . При Re < Re cr течение происходит в ламинарном режиме, при Re ≥ Re cr возможно возникновение турбулентности. Критическое значение числа Рейнольдса для течения флюида в цилиндрическом канале Re_cr ≈ 2300. Развитый турбулентный режим устанавливается при значениях Re >  1 • 10⁴, а диапазон значений Re от 2 • 10 3 до 1 . 10 4 соответствует смешанному режиму течения. Среднюю скорость течения флюида в цилиндрическом канале U можно связать с объемным расходом Q через канал следующим образом

U = 4 Qj (nD ²). (5)

В инженерных расчетах, чтобы не слишком усложнять вычисления, часто используют приближенную формулу для нахождения коэффициента теплообмена H = a + bju , где а и b — константы, определяемые из условия наилучшего согласования с данными конкретного эксперимента. Подставляя эту формулу в уравнение (3) можно получить простую связь между разностью электрических мощностей, подводимых к термочувствительным элементам, находящимся в движущейся и неподвижной жидкости, и скоростью движения жидкости в виде A P = b4u • 5 • ( T - T w ) .

Так как термочувствительный элемент работает в моде постоянной температуры, в которой температура элемента поддерживается неизменной, то, учитывая связь (5), можно получить следующую простую зависимость:

A P = k • 4Q , (6)

где k — свободный параметр, который можно определить методом наименьших квадратов, обрабатывая экспериментальные данные.

Анализируя систему уравнений (4), можно предположить, что наилучшее согласие с экспериментальными данными будет получено при использовании следующей зависимости

A P = k • Q ^Y , (7)

где параметр γ находится в интервале от до .

Аналогичным образом из выражения (2) можно получить формулу для расчета напряжения, которое необходимо приложить к термочувствитель- а

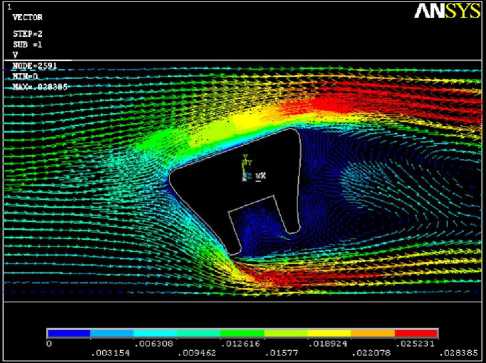
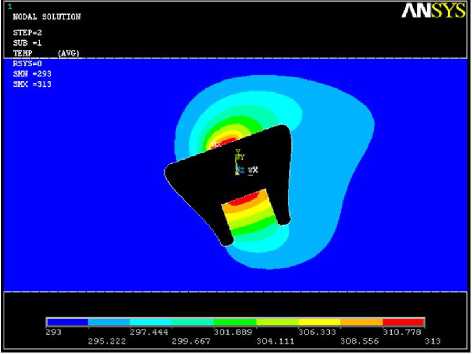
Рис. 1. Распределение скорости (a) и температуры (б) жидкости при обтекания держателя, расположенного под углом 20° к направлению набегающего со скоростью 1 · 10^–2м/с потока жидкости

б

ному элементу, находящемуся в потоке жидкости, для поддержания постоянной его температуры

V = ( aQ ^Y + в ) 2 , (8) где α и β — свободные параметры, а γ ^* — величина, которая определяется при обработке экспериментальных данных методом наименьших квадратов с использованием в качестве аппроксимирующей функции зависимости (7).

ДАТЧИК РАСХОДА ЖИДКОСТИ

Основным элементом датчика расхода жидкости является термоанемометрический микросенсор потока. В настоящей работе термочувствительные резисторы микросенсора сформированы из поликристаллического кремния методом газофазного осаждения при пониженном давлении. Толщина сформированных пленочных резисторов составила около 1 мкм. Топология сенсора, полученная методом фотолитографии, включает в себя измерительный резистор сопротивлением 150 Ом, два резистора с высоким сопротивлением (порядка 3.2 кОм) для определения температуры окружающей среды и систему проводников и контактных площадок для подключения резисторов к внешней электрической цепи (электронному блоку).

Для увеличения температурного коэффициента сопротивления α резисторов производилось легирование поликремния согласно режиму, обеспечивающему наибольшее значение α при достаточно высоком уровне линейности зависимости сопротивления от температуры. Температурный коэффициент сопротивления составил величину порядка 1∙10^–3 (К^–1).

Для защиты от воздействия агрессивной среды резисторы покрываются тонким слоем нитрида кремния. Подробно технология формирования микросенсоров на основе поликристаллического кремния описана в нашей работе [3].

Изготовленный опытный образец датчика расхода жидкости содержит следующие составляющие:

– два термоанемометрических микросенсора потока;

– держатель микросенсоров;

– электронный блок для выделения, усиления и обработки полезного сигнала;

– корпус датчика, обеспечивающий надежное крепление составных частей и герметизацию системы.

Для определения конфигурации держателя и его расположения в канале, позволяющего реализовать дифференциальный метод измерения, выполнено численное моделирование задачи методом конечных элементов с использованием прикладного пакета ANSYS [9]. В качестве примера результатов моделирования на рис. 1 предствлено распределение скорости (a) и температуры (б) жидкости при обтекании держателя, расположенного под углом 20° к направлению набегающего со скоростью 1 - 10^-2м/с потока жидкости.

На основе результатов моделирования изготовлен держатель микросенсоров, в котором один микросенсор расположен на поверхности держателя, где скорость течения жидкости близка к средней скорости в канале, а второй микросенсор — в углубленном пазу, где согласно выполненному

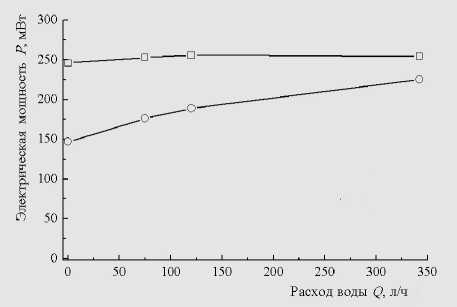
Рис. 2. Величины электрических мощностей P 1 и P 2 , подводимых к термочувствительным резисторам для поддержания постоянной разницы температур T - T w = 5 К, в зависимости от объемного расхода Q воды.

P 1— □ —, P 2 —O—

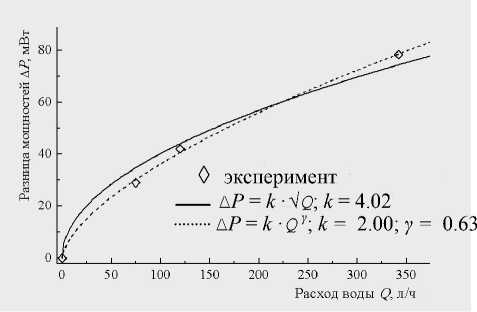
Рис. 3. Разность электрических мощностей Δ P , подводимых к термочувствительным элементам, находящимся в движущейся и неподвижной воде, как функция объемного расхода Q воды .

моделированию жидкость можно считать практически неподвижной.

Испытания опытного образца датчика расхода жидкости проводились согласно дифференциальному методу измерения в моде постоянной температуры. В качестве жидкости использовалась водопроводная вода при нормальных условиях. Объемный расход воды Q через трубу внутренним диаметром 25 мм, в которой размещался датчик, регистрировался по времени наполнения емкости объемом 10 л.

На рис. 2 представлены величины электрических мощностей P ₁ и P ₂, подводимых к термочувствительным резисторам для поддержания постоянной разницы температур T — T w = 5 К, в зависимости от объемного расхода воды. Как следует из рисунка, величина электрической мощности P 1 заметно зависит от расхода воды Q в отличие от величины P 2 , которая практически не зависит от значения Q . Таким образом, получено соответствие между результатами численного моделирования и эксперимента, что позволяет утверждать, что изготовленный согласно результатам численного моделирования держатель обеспечивает реализацию дифференциального метода измерения.

К сожалению, в настоящей работе не удалось добиться близких теплофизических характеристик двух микросенсоров, находящихся в областях движущейся и покоящейся жидкости соответственно. Действительно, как следует из рис. 2, в случае отсутствия потока воды ( Q = 0) величины подводимых электрических мощностей к резисторам для поддержания одинаковой разницы температур различны.

На самом деле такого соответствия в рамках данной работы добиться было довольно сложно т. к. работа носит изыскательский характер. В ситуации, когда изготовление микросенсоров примет массовый характер, их теплофизические характеристики будут практически идентичны. Свидетельством тому может служить интегральная технология изготовления микросенсоров [3] для датчика массового расхода воздуха ДМРВ [10]. Действительно, согласно этой технологии в одном производственном процессе проводится микромеханическая обработка партии пластин, содержащих сотни микросенсоров на каждой, за счет чего удается добиться однородности параметров микросенсоров. На данном этапе разработки ДРЖ однородность теплофизических характеристик микросенсоров не столь важна. Одной из главных достигнутых целей является верификация полученных теоретических и экспериментальных результатов.

С целью верификации разработанной в проекте аналитической модели проведем сравнение результатов модели с экспериментальными данными. Одним из результатов аналитической модели являются выражения (6) и (7), устанавливающие связь между разностью электрических мощностей Δ P , подводимых к термочувствительным элементам, находящимся в движущейся и неподвижной жидкости, и объемным расходом воды Q в канале. Так как изготовленные микросенсоры имеют различные теплофизические характеристики, то для того, чтобы произвести сравнение, необходимо воспользоваться экспериментальными данными, полученными от одного элемента, а именно

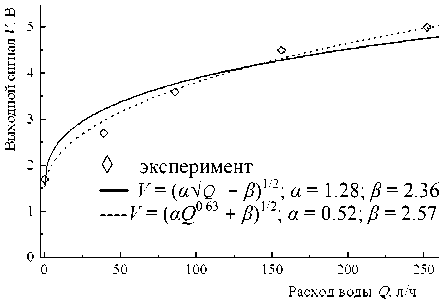
Рис. 4. Напряжение V (выходной сигнал), которое необходимо приложить к термочувствительному элементу, находящемуся в потоке воды, для поддержания постоянной его температуры, как функция объемного расхода Q воды

AP = P1 (Q)-P1 (Q = 0).

На рис. 3 представлено сравнение результатов аналитической модели с соответствующими данными эксперимента. Как и предполагалось, наилучшее согласие с экспериментальными данными получено при использовании зависимости (7). Увеличение коэффициента γ с 0.5 до 0.63 свидетельствует о наличии турбулентности в потоке воды. Действительно, как следует из системы (4), величина γ = 0.5 описывает течение флюида в ламинарном режиме. Очевидно, в настоящем эксперименте сложная конфигурация держателя может вызывать турбулизацию потока.

Выражение (8) аналитической модели представляет величину напряжения V , которое необходимо приложить к термочувствительному элементу, находящемуся в потоке жидкости, для поддержания постоянной его температуры, как функцию объемного расхода Q жидкости. На рис. 4 представлены экспериментальная и теоретическая зависимости напряжения V (выходной сигнал) от величины расхода воды Q в канале. Как следует из рисунка, наблюдается согласие между результатами аналитической модели и экспериментальными данными. Как и в предыдущем случае, наилучшее согласие получено при γ = 0.63.

ЗАКЛЮЧЕНИЕ

Основными результатами выполненной работы являются:

– аналитическая модель термоанемометрического сенсора потока;

– термоанемометрический микросенсор для датчика расхода жидкости;

– опытный образец датчика расхода жидкости;

– результаты испытаний датчика.

По результатам работы можно сформулировать следующие основные выводы.

– Разработанная аналитическая модель термоанемометрического сенсора потока удовлетворительно описывает полученные в работе экспериментальные результаты.

– Микросенсор прост по конструкции, компактен, универсален по использованию, изготовлен без применения драгоценных металлов, имеет надежно защищенную поверхность. Конструкция и технология изготовления сенсора потока обеспечивают возможность массового производства, проведения всех последующих операций сборки в состав устройства и надежной эксплуатации.

– Предложенная конфигурация держателя микросенсоров датчика расхода жидкости позволяет реализацию дифференциального метода измерения расхода.

– Испытания опытного образца датчика расхода жидкости согласно дифференциальному методу измерения показали, что уровень выходного сигнала достаточен для проведения измерений расхода жидкости в широком диапазоне величин.

В целом полученные результаты важны для конструирования, производства и оптимизации датчиков расхода флюида и позволяют самостоятельно производить разработку и промышленное изготовление подобных датчиков, используя производственные мощности НПО Автоматики им. акад. Н.А. Семихатова. Подробно некоторые аспекты представленной научно-исследовательской работы отражены в отчете [11].

Работа поддержана государственным контрактом № П 360 и грантом российского правительства № 11.G34.31.0064.