Deep Hybrid System of Computational Intelligence with Architecture Adaptation for Medical Fuzzy Diagnostics
Автор: Iryna Perova, Iryna Pliss
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 7 vol.9, 2017 года.
Бесплатный доступ
In the paper the deep hybrid system of computational intelligence with architecture adaptation for medical fuzzy diagnostics is proposed. This system allows to increase a quality of medical information processing under the condition of overlapping classes due to special adaptive architecture and training algorithms. The deep hybrid system under consideration can tune its architecture in situation when number of features and diagnoses can be variable. The special algorithms for its training are developed and optimized for situation of different system architectures without retraining of synaptic weights that have been tuned at previous steps. The proposed system was used for processing of three medical data sets (dermatology dataset, Pima Indians diabetes dataset and Parkinson disease dataset) under the condition of fixed number of features and diagnoses and in situation of its increasing. A number of conducted experiments have shown high quality of medical diagnostic process and confirmed the efficiency of the deep hybrid system of computational intelligence with architecture adaptation for medical fuzzy diagnostics.
Computational intelligence, medical data mining, classification, fuzzyfication, growing hybrid system, deep hybrid system
Короткий адрес: https://sciup.org/15010945
IDR: 15010945
Текст научной статьи Deep Hybrid System of Computational Intelligence with Architecture Adaptation for Medical Fuzzy Diagnostics
Published Online July 2017 in MECS
Necessity of improving medical diagnostics quality is one of the most disputed problems of medicine in the whole world. The certain authors proposed to use systems of Computational Intelligence to solve this problem [1-5] and an area of Medical Data Mining shows increasing medical diagnostics quality. Nowadays there are many important tasks in the Medical Data Mining area, like medical diagnostics (classification, clusterization, pattern recognition and so on), compressing, prediction etc. The methods of Computation Intelligence, especially Machine Learning and Soft Computing, are widely used for solving all these tasks [6-14]. It’s important to note that in medical diagnostics tasks the most effective systems are artificial neural networks [9,15,16,18], fuzzy and hybrid systems [17] and neuro-fuzzy systems [6,13], due to their capacity for approximation of properties, capability to learning (including self-learning), transparency of obtained results. These systems can realize processing of medical data sets more adequately and with higher precision.
The medical diagnostics task is one of problems of pattern recognition where classes-diagnoses can have random quantity, form and can overlap. Previously many authors tried to create systems of Computational Intelligence for medical diagnostics tasks using different datasets from Medical Repositories as an input data [1938]. But all these systems have common disadvantages, like impossibility to process data in online mode, fixed number of features and diagnoses, low rate of convergence. In [20] authors have obtained an accuracy of 79.37% for the Pima Indians diabetes dataset and an accuracy of 97.55% for dermatology dataset using a relatively new architecture for evolving fuzzy rule-based systems (eClass). Authors [26] have proposed to use probabilistic neural network (PNN) for Pima Indian diabetes diagnostics which gave an accuracy of 78,05%.. In [25] using method, based on Radial Basis and Back-propagation Neural Networks (BNN) the authors have obtained an increase inaccuracy of up to 1.2% in comparison with the baseline on diabetes dataset. In 2011 authors [27] have proposed to process small medical data sets using fuzzy-based non-linear transformation method. The experiment results indicated that the proposed method has better classification performance than either PCA or kernel principal component analysis (KPCA) in the case when the data set is small. In 2014 authors [19] processed medical data sets utilizing hybrid fuzzy wavelet neural network and learning based optimization algorithm. The proposed method has achieved an accuracy of 84.24% for Pima Indians diabetes dataset. In [23] authors have reached 82.59% classification accuracy for Statlog Heart Disease and obtained a classification accuracy of 75.87% for Pima Indians Diabetes using Attribute Weighted Artificial Immune System (AWAIS).
But all these systems have fixed architecture, i.e. quantity of inputs and outputs can’t be changed, that means that system can not adapt its architecture. In this paper a new deep multilayer hybrid system of computational intelligence with architecture adaptation for medical fuzzy diagnostics is proposed to increase the efficiency of the medical diagnosis process.
The rest of this paper is organized as follows: section two represents architecture of a deep hybrid system for fuzzy diagnostics and algorithms of its training; section three represents growing deep hybrid system for fuzzy medical diagnostics and algorithms of its training; section four describes the experimental results of using of proposed system on medical datasets (dermatology, Pima Indians diabetes and Parkinson disease datasets) and discusses the experimental results.
-
II. Deep Hybrid System for Fuzzy Diagnostics
Let’s introduce into consideration architecture of hybrid system for fuzzy diagnostics that consists of six sequentially connected layers (fig.1).
The first hidden layer of system under consideration contains hn membership functions цп ( x ( k ) ) , i = 1,2,..., n ; l = 1,2,..., h and provides fuzzyfication of input feature space.
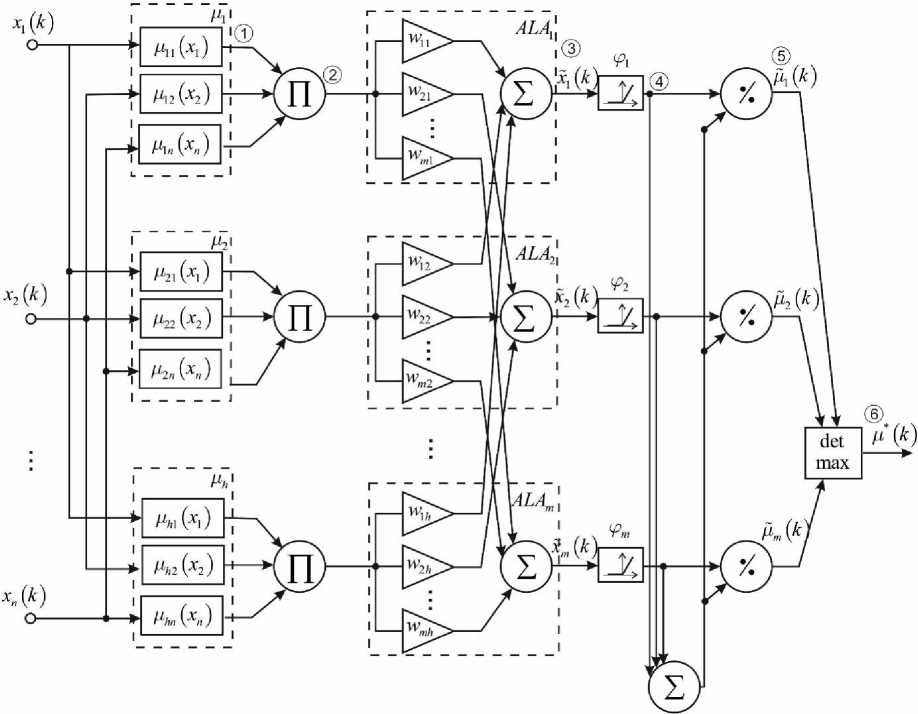
Fig.1. Deep hybrid system for fuzzy diagnostic with n inputs and m outputs
System scatter partitioning of features space is realized by membership functions with standard bell shape constructions with unlimited supports. Most often they are traditional Gaussians
Mu(Xi( k )) = exp
( x i ( k ) - c ii ) 2 )
2 ^' ) ,
where c – parameter of center-function (in simplest case centers are evenly distributed in interval [0,1] with step ( h - 1) - 1), ^- - width parameter which can be chosen empirically or turned using backpropagation [34]. Fig.2 presents these membership functions.
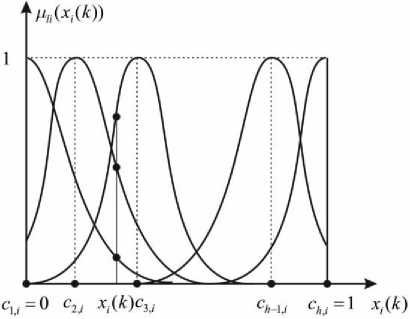
Fig.2. Bell shape membership functions of first hidden layer
The second hidden layer realizes aggregation of membership levels, that were calculated in the first layer, n and consists of h multipliers: xt = ПAu (xt (k)) • i=1
The third hidden layer is a layer of m adaptive linear associators (ALA) with tuning weights w :
hn h xj (k)=S wi П a (x (k))=S wixi (k),j=ь2,-, m • l=1 i=1 i=1
The fourth hidden layer consists of nonlinear activation functions of special type [35]:
u j ( k ) = H x j ( k ) ) =
' xj ( k )
if Xj (k) > 0, if Xj (k) < 0, j = 1,2,...,m .
d ( k ) = ( d 1 ( k ) , d 2 ( k ) ,..., dm ( k )) T - reference signals vector, which components can take only two values 0 or 1; x ( k ) = ( x ( k ) I m , x ( k ) I m ,..., x h ( k ) I m ) T - vector of second layer outputs, Im = ( m x 1 ) -unit vector;
x ( k ) = ( X ( k ) , x 2 ( k ) ,..., xm ( k ) ) T - vector of third layer outputs;
e ( k ) = ( e ( k ) , e 2 ( k ) ,..., em ( k ) ) T - vector of training errors;
The fifth hidden layer is formed by single adder and m division units, where defuzzyfication of “gravity centers” type is realized in the form
a , ( k ) =
uj ( k )
г
^ | S wax i
V i = 1
m
S j k )
j = 1
mh
S d S w a xi ( k ) j = 1 V i = 1
г
^| S wji П aA xi(k))
V i = 1 i = 1
mh n
S^iS wn П a»( xi( k))
j = 1 V i = 1 i = 1
j = 1,2,..., m .
And last output sixth layer is formed by maximum detector which extracts the most probable diagnosis A ( k ) = max { a ( k ) , ^ 2 ( k ) ,..., A m ( k ) } .
For training of this system we have used conventional criterion [35]:
E, ( k ) = jl d ( k ) - x ( k 1 (2)
and algorithm for synaptic weights matrix tuning in the form
W ( k + 1 ) = W ( k ) +
e ( k) x T ( k ) II-X( k )l Г
= W ( k ) +
(d(k)-W(k)x(k))xT (k)
= W (k) + (d (k)-W (k) x (k)) x+ (k),
-
III. Growing Deep Hybrid System for Fuzzy Medical Diagnostics
In medical tasks a situation when number of input and output parameters can change during processing happens often. This changing can be interpreted like growing of quantities of input and output parameters (for example a new medical parameter was measured or patient has different diagnoses that are described by same symptoms). So creating of system, which can realize this growing is an actual task.
In Fig. 3 the architecture of introduced system with growing number of inputs ( n + 1) and outputs ( m + 1) is presented.
The input vector of signals-attributes for ( n + 1) features can be presented by vector
The first hidden layer of system contains h ( n + 1) membership functions a ( xi ( k ) ) , i = 1,2,..., n + 1 ;
i = 1,2,..., h for fuzzyfication of input features space. Second hidden layer realizes aggregation of membership n + 1
levels and consists of h multipliers x ˆ = П A ii ( x. ( k ) ) .
i = 1
The third hidden layer contains ( m + 1 ) adaptive linear associators (ALA):
-
h n + 1 h
xi (k)=S wji П An (x (k))=S wjxi (k),
-
I = 1 i = 1 i = 1
j = 1,2,..., m + 1.
The fourth hidden layer consists of nonlinear activation functions [34]:
uj (k) = d( xj (k))=
xj ( k )
I x j ( k ) > 0
I xA k ) ^ 0,
j = 1,2,..., m + 1.
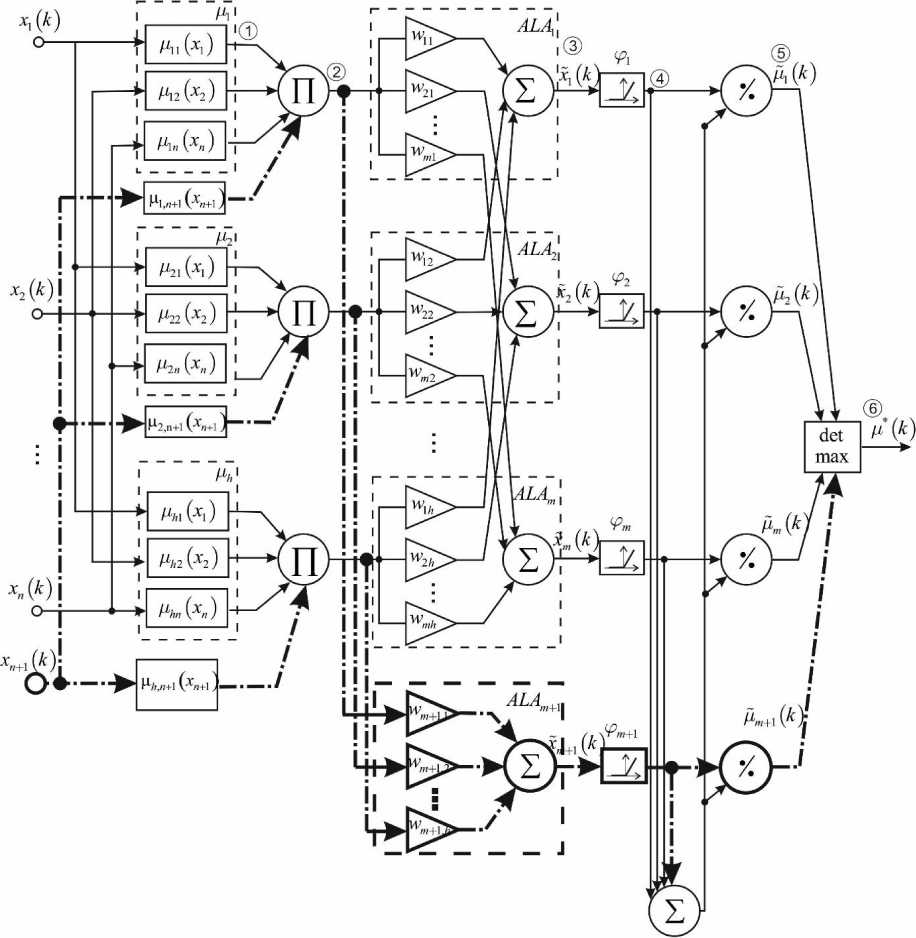
Fig.3. Growing deep hybrid system of computational intelligence
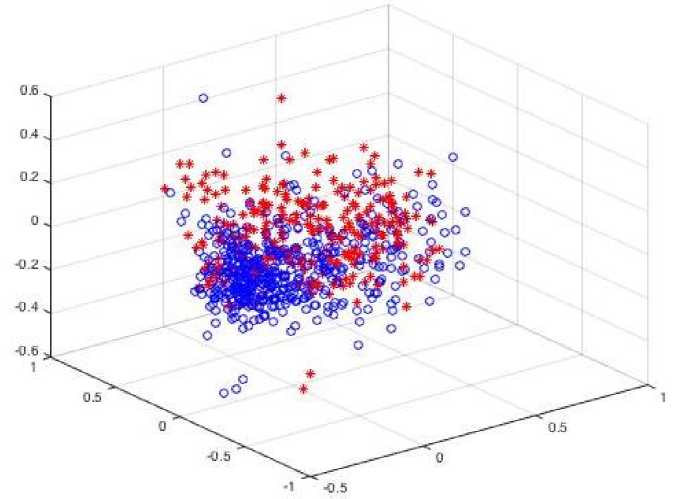
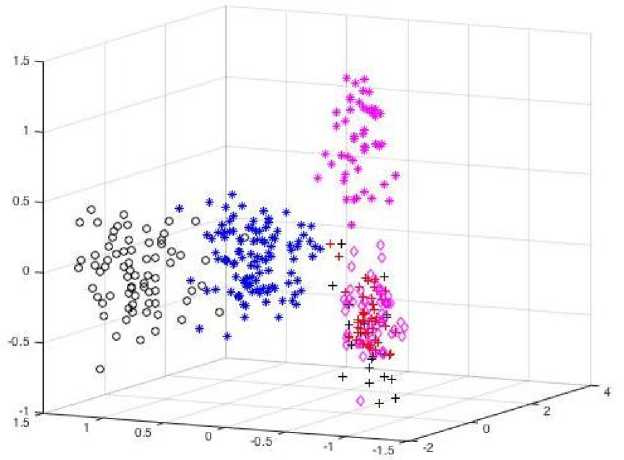
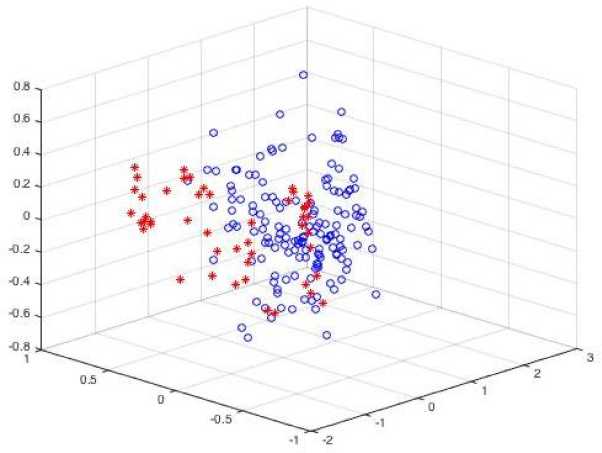
The fifth hidden layer is formed by single adder and m +1 division units for defuzzyfication of «gravity centers» type d|E wj-x-(k )l й Hj \'4 m+1 m+i hh Euj(k) E^IEwix- (k) j=1 j=1 V -=1 h ^IE wji П Hu( xi( k)) V l=1 m+1 h EdE w- П H-,( x( k)) j=1 V -=1 j = 1,2,..., m +1. The output layer extracts the most probable diagnosis Ц (k) = max {H1 (k) , Ц2 (k) ,...,Hm (k) , Hm+1 (k)} . Thus in our system blocks of fuzzyfication were introduced into first system’s layer, one more ALA-block into third layer, one more nonlinear activation function at fourth layer and one more division unit for defuzzyfication of «gravity centers» type. It is easy to see that all introduced blocks do not change essentially architecture of the system under consideration. For training this system we can use criterion (2). For tuning synaptic weights at the first step we need to perform concatenation of matrix W with new weights-vector, which correspond to new diagnosis. At the next step we use an algorithm for synaptic weights matrix tuning (3) in the form: x(k) = (x (к)Im,x2 (к)Im,...,xh (к)IT )T-vector of second layer outputs; Im =( m x1) -unit vector em+1(k) = (eT (k) : em+1(k))T - vector of training-errors for m +1 diagnosis. So matrix of synaptic weights transforms into the form of ((m + 1)x mh) one: W* ^ w11 (k) w21 ( k ) w12 (k) .' w22 (k) .. ■. w1 h (k) ■. W2 h ( k ) W * (k ) = wm1 ( k ) wm2 (k) .. . wm.(k) , w( m+1)1 ( k ) w(m+1)2 (k) .. •. w( m+1) h(k )J It is easy to see that we have no need to retraining the synaptic weights which have been tuned at previous situation of m diagnoses. + W (k) d ( k) x ( k) ———— dm+1 ( k ). ———— . ^+1 ( k У — ———— x T (k ) + xm+1 ( k ). d (k ) x (k) ———— dm+1 ( k ) — ———— x + (k), . xm+1 ( k ). The Pima Indians diabetes dataset [36] contains 768 instances. Number of attributes is 8 plus class-diagnosis (value 1 is interpreted as tested positive for diabetes, 500 instances, 0 – tested negative for diabetes, 268 instances). All attributes are numeric-valued, information about them is presented in Table 1. where dm+1 (k) = (dT (k) : dm+1 (k)) - reference signals vector for m +1 diagnosis; Table 1. Attribute information Attribute number in data folder Attribute characteristics 1 Number of times pregnant 2 Plasma glucose concentration a 2 hours in an oral glucose tolerance test 3 Diastolic blood pressure (mm Hg) 4 Triceps skin fold thickness (mm) 5 2-Hour serum insulin (mu U/ml) 6 Body mass index 7 Diabetes pedigree function 8 Age (years) 9 Class variable (0 or 1) The Pima Indians diabetes dataset visualization using principal component analysis is presented in Fig.4. It is easy to see that it contains 2 overlapped classes-diagnoses and for its processing we need to use fuzzy procedures. The dermatology dataset [37] contains 366 instances, but some of attributes has missed values. After deleting gaps number of instances became 358. Number of attributes is 34 plus class-diagnosis (value 1 is interpreted as psoriasis, 112 instances; 2 – seboreic dermatitis, 61 instances; 3 – lichen planus, 72 instances; 4 – pityriasis rosea, 49 instances; 5 – cronic dermatitis, 52 instances; 6 – pityriasis rubra pilaris, 20 instances). Fig.4. The Pima Indians Diabetes dataset visualization «*» - tested negative for diabetes «o» – tested positive for diabetes All attributes (excepting age and family history feature) are given a degree in the range of 0 to 3,where 0 indicates that the feature was not present, 3 indicates the largest amount possible and 1, 2 indicate the relative intermediate values. The family history feature has the value of 1 if any of these diseases has been observed in the family, and 0 otherwise. The age feature simply represents the age of the patient. Features information is presented in Table 2. Table 2. Attribute information Attribute number in data folder Attribute characteristics Clinical Attributes 1 erythema 2 scaling 3 definite borders 4 itching 5 koebner phenomenon 6 polygonal papules 7 follicular papules 8 oral mucosal involvement 9 knee and elbow involvement 10 scalp involvement 11 family history 34 age Histopathological Attributes 12 melanin incontinence 13 eosinophils in the infiltrate 14 PNL infiltrate 15 fibrosis of the papillary dermis 16 exocytosis 17 acanthosis 18 hyperkeratosis 19 parakeratosis 20 clubbing of the rete ridges 21 elongation of the rete ridges 22 thinning of the suprapapillary epidermis 23 spongiform pustule 24 munro microabcess 25 focal hypergranulosis 26 disappearance of the granular layer 27 vacuolisation and damage of basal layer 28 spongiosis 29 saw-tooth appearance of retes 30 follicular horn plug 31 perifollicular parakeratosis 32 inflammatory monoluclear inflitrate 33 band-like infiltrate The dermatology dataset visualization using principal component analysis is presented in Fig.5. It is easy to see that it contains 4 linearly-separated classes-diagnoses, one of which contains 3 overlapped subclasses. Fig.5. The dermatology dataset visualization «*» - cronic dermatitis; «о» - lichen planus; «*» - psoriasis; «+» - pityriasis rubra pilaris; «+»- pityriasis rosea; «◊» - seboreic dermatitis. The Parkinson dataset [38] is composed of a range of biomedical voice measurements from 31 people, 23 with Parkinson's disease. The each column in the table is a particular voice measure, and each row corresponds to one of 195 voice recordings from these individuals ("name" column). The main aim of the data is to discriminate healthy people from those with Parkinson's disease, according to "status" column which is set to 0 for healthy and 1 for Parkinson's disease. Attribute information is presented in table 3. Table 3. Attribute information Attribute name in data folder Attribute characteristics name ASCII subject name and recording number MDVP:Fo(Hz) average vocal fundamental frequency MDVP:Fhi(Hz) maximum vocal fundamental frequency MDVP:Flo(Hz) minimum vocal fundamental frequency MDVP:Jitter(%), MDVP:Jitter(Abs), MDVP:RAP, MDVP:PPQ, Jitter:DDP several measures of variation in fundamental frequency MDVP:Shimmer, MDVP:Shimmer(dB), Shimmer:APQ3, Shimmer:APQ5, MDVP:APQ, Shimmer:DDA several measures of variation in amplitude NHR, HNR two measures of ratio of noise to tonal components in the voice Status health status of the subject: (one) - Parkinson's, (zero) - healthy RPDE, D2 two nonlinear dynamical complexity measures DFA signal fractal scaling exponent spread1, spread2, PPE three nonlinear measures of fundamental frequency variation Fig.6. The Parkinson dataset visualization At the first step input information from all datasets has been standardized and normalized using expression X ( k ) = X,(k) - X, min Z X / v V i max imin that corresponds to encoding all input data in the interval x, E [0,1]. After that columns which correspond to health status of the subject (5-th for Iris Fisher dataset, 9-th for Pima Indians Diabetes dataset, 35-th for Dermatology dataset and 17-th – in Parkinson dataset) were moved from the table «Object-Properties»to vector d(k) and all datasets were processed using proposed deep hybrid system for fuzzy diagnostics for n inputs and m outputs. As a result we have used the percent of incorrect classified patterns in training and test sample. Results are presented in Table 4. Table 4. Result of classification using deep hybrid system for fuzzy diagnostic for n inputs and m outputs Dataset Percent of incorrect classified patterns Training set Testing set Iris 1,5% 3% Dermatology 2,4% 13% Pima Indians Diabetes 0,25% 6,66% Parkinson 0,76% 3,55% At the next step one attribute was deleted from all datasets. System was trained on n attributes, after that this attribute was returned. Classification results are shown in Table 5. Table 5. Result of classification using deep hybrid system for fuzzy diagnostic for n +1 inputs and m outputs Percent of incorrect classified patterns for n attributes Percent of incorrect classified patterns for (n+1) attributes training testing training testing Iris 1,4% 2,68% 3,57% 8,23% Dermatology 0,87% 6,5% 4,75% 16,55% Pima Indians Diabetes 0,45% 7,33% 0,25% 7,94% Parkinson 1,33% 4,66% 0,56% 7,92% Then one class-diagnosis was deleted from all datasets. The system was trained on n + 1 attributes and m diagnoses, after that patients with deleted diagnosis were returned. The classification results are shown in Table 5. Table 6. Result of classification using deep hybrid system for fuzzy diagnostic for n +1 inputs and m +1 outputs Percent of incorrect classified patterns for m diagnoses Percent of incorrect classified patterns for (m+1) diagnoses training testing training testing Iris 1% 2% 9% 16,6% Dermatology 0,5% 4% 13,16% 20% We have to note that all results were averaged after 50 epochs. The deep hybrid system of computational intelligence with architecture adaptation and its training algorithms for medical diagnostic tasks are proposed. The system approbation is confirmed on three medical datasets and has is shown the high level of results in conditions of overlapped classes-diagnoses, small datasets and changing number of features and diagnoses. [35] A. Cichocki, R. Unbehauen Neural Networks for Optimization and Signal Processing. – Stuttgart: Teubner, 1993. – 526 p. [36] Pima Indians Diabetes dataset. Available from: http://archive.ics.uci.edu/ml/machine-learning-databases/pima-indians-diabetes/pima-indians-diabetes.data. Accessed: 1st of May, 2008. [37] Dermatology dataset. Available from: databases/dermatology/ Accessed: 1st of May, 2008. [38] Parkinson dataset. Available from: Accessed: 1st of May, 2008. [39] Iris dataset, Available from: Accessed: 1st of May, 2008. Research interests include computational intelligence, data mining: fuzzy clustering algorithms based on neuro-fuzzy models. She has more than 150 publications and five inventions. At present, she is a Leading Researcher at the Control Systems Research Laboratory, Kharkiv National University of Radio Electronics. She is the IEEE Signal Processing Society and the Neural Network Society member.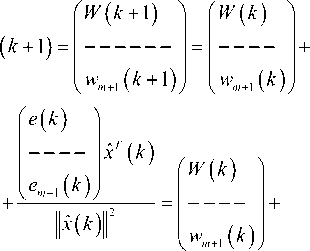
V. Conclusion
Список литературы Deep Hybrid System of Computational Intelligence with Architecture Adaptation for Medical Fuzzy Diagnostics
- JJ. S. Bhalla, A. Aggarwal A novel method for medical disease diagnosis using artificial neural networks based on backpropagation algorithm. –Confluence 2013: The Next Generation Information Technology Summit (4th International Conference). – 2013. – pp.55-61.
- R. Isola , R. Carvalho, M. Iyer, A. K. Tripathy Automated Differential Diagnosis in Medical Systems Using Neural Networks, kNN and SOM. – Developments in E-systems Engineering (DeSE), 2011. – pp.62-67.
- F. Jiménez, G. Sánchez, J.M. Juárez Multi-objective evolutionary algorithms for fuzzy classification in survival prediction. – Artificial Intelligence in Medicine 60 (2014). – pp. 197-219. DOI: 10.1016/ j.artmed.2013.12.006
- Y. Bodyanskiy, A. Dolotov, O. Vynokurova Evolving spiking wavelet-neuro-fuzzy self-learning system // Applied Soft Computing Journal. - 2014. - 14. - P. 252-258. DOI: 10.1016/j.asoc.2013.05.020
- Ye.V. Bodyanskiy, E.A. Vynokurova, A.I. Dolotov, Self-learning cascade spiking neural network for fuzzy clustering based on group method of data handling // Journal of Automation and Information Sciences. – 2013. – 45(3). – P.23-33. DOI: 10.1615/JAutomatInfScien.v45. i3.30
- J.-S.R. Jang Neuro-Fuzzy and Soft Computing / J.-S.R. Jang, C.-T. Sun, E. Mizutani. – Prentice Hall, Upper Saddle River, NJ. – 1997. – 640 p.
- J. Friedman The Elements of Statistical Learning. Data Mining, Inference and Prediction / Friedman J., Hastie T., Tibshirani R. – Berlin: Springer, 2003. – 552 p.
- E. Bodyanskiy, A. Dolotov Image processing using self-learning fuzzy spiking neural network in the presence of overlapping classes. – Proc. 11-th Int. Biennial Baltic Electronics Conf. BEC2008. – Tallinn, Estonia, 2008. – P. 213-216.
- L. Ruthowski, "Computational Intelligence. Methods and Techniques", Berlin-Heidelberg: Springer-Verlag, 2008. – 514 p.
- C.L. Mumford, L.C Jain. Computational Intelligence. Collaboration, Fusion and Emergence. – Berlin: Springer-Verlag, 2009. – 725p.
- R. Kruse, C. Borgelt, F. Klawonn, C. Moewes, M. Steinbrecher, P. Held Computational Intelligence. Methodological Introduction. – Berlin: Springer-Verlag, 2013. – 488p.
- A. Kroll Computational Intelligence. Eine Einführung in Probleme, Methoden und technische Anwendungen. – Muenchen: Oldenbourg Verlag, 2013. – 428 S.
- K.-L. Du, M.N.S. Swami, Neural Networks and Statistical Learning, London: Springer-Verlag, 2014. – 824 p.
- I. Izonin, R. Tkachenko, D. Peleshko, T. Rak and D. Batyuk, "Learning-based image super-resolution using weight coefficients of synaptic connections," Scientific and Technical Conference "Computer Sciences and Information Technologies" (CSIT), 2015 Xth International, Lviv, 2015, pp. 25-29. doi: 10.1109/STC-CSIT.2015.7325423
- C.M. Bishop, Neural Networks for Pattern Recognition, Oxford: Clarendon Press, 1995. – 482 p.
- S. Haykin, Neural Networks. A Comprehensive Foundation, Upper Saddle River, N.J.: Prentice Hall, Inc., 1999. – 842 p.
- J.C. Bezdek, J. Keller, R. Krisnapuram, N.R. Pal, Fuzzy Models and Algorithms for Pattern Recognition and Image Processing, Springer 2005. – 776 p.
- Zh. Hu, Ye. V. Bodyanskiy, O. K. Tyshchenko, V. O. Samitova, Fuzzy Clustering Data Given on the Ordinal Scale Based on Membership and Likelihood Functions Sharing, I.J. Intelligent Systems and Applications (IJISA), Vol.9(2), pp.1-9, 2017. DOI: 10.5815/ijisa.2017.02.01
- H. Kahramanli, N. Allahverdi, "Design of a hybrid system for the diabetes and heart diseases," Expert Systems with Applications, vol. 35, no. 1-2, pp. 82–89, 2008. DOI: 10.1016/j.eswa.2007.06.004
- S. Lekkas, L. Mikhailov Evolving fuzzy medical diagnosis of Pima Indians diabetes and of dermatological diseases. – Artificial Intelligence in Medicine 50 (2010). – pp. 117–126. DOI: 10.1016/j.artmed.2010.05.007
- K. Polat, S. Gunes, A. Arshlan A cascade learning system for classification of diabetes disease: generalized discriminant analysis and least square support vector machine. Expert Systems with Applications. 2008; 34, pp. 482–487. DOI:10.1016/j.eswa.2006.09.012
- K. Kayaer, T. Yildirim Medical diagnosis on Pima Indian diabetes using general regression neural networks. in: Proceedings of international conference on artificial neural networks neural information processing. – 2003. – pp.181–184.
- S. Sahan, K. Polat, H.Kodaz, S. Gunes The medical applications of attribute weighted artificial immune system (AWAIS): diagnosis of hearts and diabetes diseases. Proc. ICARIS'05 Proceedings of the 4th international conference on Artificial Immune Systems. – pp. 456–468. DOI: 10.1007/11536444_35
- W.Luangruangrong ; A. Rodtook ; S.Chimmanee Study of Type 2 diabetes risk factors using neural network for Thai people and tuning neural network parameters. – 2012 IEEE International Conference on Systems, Man, and Cybernetics (SMC). – 2012. – pp. 991 – 996. DOI: 10.1109/ICSMC.2012.6377858
- H. Temurtas, N. Yumusak, F. Temurtas A comparative study on diabetes disease diagnosis using neural networks. – Expert Systems with Applications 36 (2009). – pp. 8610–8615. DOI: 10.1016/j.eswa.2008.10.032
- C.C. Bojarczuk, H.S. Lopes, A.A. Freitas, E. L. Michalkiewicz A constrained-syntax genetic programming system for discovering classification rules: application to medical data sets. – Artificial Intelligence in Medicine, 2004, Volume 30, Issue 1, Pages 27–48. DOI: 10.1016/j.artmed.2003.06.001
- Der-Chiang Li, Chiao-Wen Liu, Susan C. Hu A fuzzy-based data transformation for feature extraction to increase classification performance with small medical data sets. – Artificial Intelligence in Medicine, 2011, Volume 52, Issue 1, Pages 45–52. DOI: 10.1016/j.artmed.2011.02.001
- Z. Beheshti, S. M. H. Shamsuddin, E. Beheshti, and S. S. Yuhaniz, Enhancement of artificial neural network learning using centripetal accelerated particle swarm optimization for medical diseases diagnosis, Soft Computing, pp. 1–18, 2013. DOI: 10.1007/s00500-013-1198-0
- Ye. Bodyanskiy, O. Vynokurova, P. Mulesa, T. Tverdokhlib, V. Savvo Hybrid Clustering-Classification Neural Network in the Medical Diagnostics of the Reactive Arthritis // Int. J. Intelligent Systems and Applications. – 2016. – 8. – P. 1-9. DOI: 10.5815/ijisa.2016.08.01
- D. Peleshko, T. Rak, I. Izonin Image Superresolution via Divergence Matrix and Automatic Detection of Crossover // International Journal of Intelligent Systems and Applications (IJISA), 2016. - Vol. 8, No. 12. - P.1-8. DOI: 10.5815/ijisa.2016.12.01
- Ye. Bodyanskiy, O. Tyshchenko, and A. Deineko, An Evolving Radial Basis Neural Network with Adaptive Learning of Its Parameters and Architecture, Automatic Control and Computer Sciences, Vol. 49, No. 5, pp. 255-260, 2015. DOI: 10.3103/S0146411615050028
- Zh. Hu, Ye.V. Bodyanskiy, O.K. Tyshchenko, and O.O. Boiko, An Evolving Cascade System Based on a Set of Neo-Fuzzy Nodes, International Journal of Intelligent Systems and Applications (IJISA), Vol. 8(9), pp.1-7, 2016. DOI: 10.5815/ijisa.2016.09.01
- Zh. Hu, Ye.V. Bodyanskiy, O.K. Tyshchenko, and V.O. Samitova,Fuzzy Clustering Data Given in the Ordinal Scale, International Journal of Intelligent Systems and Applications (IJISA), Vol.9, No.1, pp.67-74, 2017. DOI: 10.5815/ijisa.2017.01.07
- S. Osowski Sieci neuronowe do przetwarzania informacji, Warszawa Oficyna Wydawnicza Politechniki Warszawskiej, 2006. – 422s.
- A. Cichocki, R. Unbehauen Neural Networks for Optimization and Signal Processing. – Stuttgart: Teubner, 1993. – 526 p.
- Pima Indians Diabetes dataset. Available from: http://archive.ics.uci.edu/ml/machine-learning-databases/pima-indians-diabetes/pima-indians-diabetes.data. Accessed: 1st of May, 2008.
- Dermatology dataset. Available from: http://archive.ics.uci.edu/ml/machine-learning-databases/dermatology/dermatology.data. Accessed: 1st of May, 2008.
- Parkinson dataset. Available from: http://archive.ics.uci.edu/ml/machine-learning-databases/parkinsons/parkinsons.data. Accessed: 1st of May, 2008.
- Iris dataset, Available from: http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data. Accessed: 1st of May, 2008.


