Defect Analysis Using Artificial Neural Network

Published Online April 2013 in MECS

• I.    Introduction

  Ceramic tile is one of the most needed building materials, numbering thousand-year history, and until now does not get out of fashion, and continues to be improved from year to year. In accordance with the growth in tile demand, there have been some shifts in the world ceramic tile industry [1]. In 1990, Europe accounted for 54% of world ceramic tile production. By 2002, Europe was down to 25% of world ceramic tile production. In 2005, world ceramic tile production was about 7 billion sq. meters, of which China produced 35%, and Spain, Italy, and Brazil shared the next 25%, with their production spaced neck and neck [2].

Although tile production has increasingly been subject to the introduction of automated technology, with high speed lines now approaching production rates in the order of 200 tiles/min. The control of tile quality is considered fundamental to the maintenance of market share, has often remained essentially a manual operation. Potential, therefore, exists for the increased application of automated inspection, and the effective use of product quality data in the closed-loop control of automated production [3]. The displacement of manual tile inspection procedures through the introduction of automated techniques offers a number of significant commercial and social advantages, including the elimination of human error and/or subjective judgment, improved operational efficiency, and the creation of timely statistical product data, improved safety, better working conditions and reduced labor costs. These important considerations are regarded as fundamental in order to secure a mechanism for competitive improvements within the world tile manufacturing market.

In the production line of ceramic tile industry, several problems can turn into failures of the final product. Among these failures, one of the most important and difficult to monitor is delimitation or void. It manifests itself through layers of parallel air pockets of the pressed material that retain air. Since delimitation produces stress concentrations with high propagation of failures, timely detection of cracks in the structure may help in preventing such failures. Tiles are normally subject to a complete sorting operation at the end of the production cycle, in order to identify all defects, or at the exit of kiln, exclusively for identifying the superficial defects [5].

• II.    Methodology

In this paper, matrix value of the tile is connected with Artificial Neural Networks (ANN) for automatic process fault detection in ceramic tile [6]. Artificial neural networks can be seen as highly parallel dynamical systems consisting of multiple simple units that can perform transformation by means of their state response to their input information. How the transformation is carried out depends on the Neural Network (NN) model and its way of learning the transformation. Neural network learns by example. In a typical scenario, a neural network is presented iteratively with a set of sample, known as the training set, from which the network can be trained

• III.    Nomenclature

x i(p), x2(p),-■-, xn(p) = input binary matrix yd,i(p), yd,2(p),- -, yd,n(p)= desired output sigmoid = activation function

Awyk(p) = «■ У y(p) • 5k (p)

Where n is the number of inputs of neuron j in the hidden layer

y _; ( p ) = sigmoid

y_k ( p ) = sigmoid

n

E x(p) • w(p) -° j

. i = 1

m

E xk( p )' wk( p ) -° k i=1

Where m is the number of inputs of neuron k in the output layer

ek(p) = yd, k(p) - Ук(p)

w 1 ( p ), w 2 ( p ),…, w n ( p )= weight given to neuron

^ (p) = error gradiant

Where

5k (p) = Ук ( p ).[1 - Ук ( p )].ek ( p )

AWjk (p) = weight correction

Where

• IV.    Defects Detection in Ceramic Tile

As well as many other industries, surface inspection and quality classification is an essential stage in tile manufacturing. Due to the high cost of human inspection, speed of the production line, and repetitious nature of the activity, development of a suitable Automatic Defect Detection System (ADDS) would have an impressive impact on the overall performance of a tile production plant. The key point is eventually being at the performance zenith, which guarantees the success in a very competitive market.

Further development to the other stages of the production line: It is possible to spread a modular ADDS throughout the production line to gain a more effective and robust quality control process. Fault prediction and correction, and recycling the defective materials before the kiln will be some of the advantages of such an advanced system.

Following table illustrates the typical defects for a ceramic tile.

Defect	Characteristics
Broken corners and edges	Physical damages on corners and edges
Color grading	Changes in color shades
Cracks	Thin and long random physical defects
Dirt	Small random particles on the surface
Drops	Include color and water drops
Lines	Wide visible direct lines on tile surface, mostly result of production line bars
Pinholes	Very small holes
Textural problems	Changes in density and shape of patterns

• V.    Artificial Neural Network for Defect Detection

Detection is the process of MANIPULATING binary matrix into a finite number of individual classes or categories of data based on their original values. If a matrix satisfies a certain set of criteria, then the matrix is assigned to the class that corresponds to that criterion.

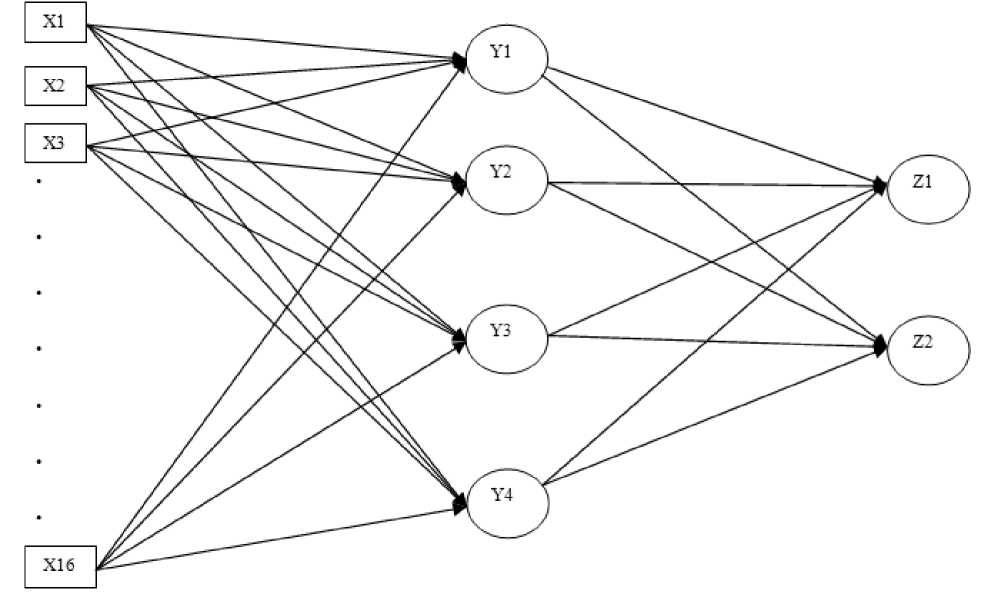
The most widely used neural classifier is multilayer perceptron network which has been extensively analyzed and for which many learning algorithms have been developed. The MLP belongs to the class of supervised neural networks. The multi-layer perceptron neural network model consists of a network of processing elements or node arrangement in the layers. Typically, it requires three or more layers of processing nodes: an input layer which accepts the input variables used in the classifier procedure, one or more hidden layers, and an output layer with one node per class. A number of neurons in the input layer depend on the features’ vector, and in the output layer are based on the number of classes. In this study, a three-layer network has been constructed with 16 neurons in input layer, 4 neurons in hidden layer and 2 neurons in output layer.

There are several training algorithms for feed forward networks. All of these algorithms use the gradient of the performance function to determine how to adjust the weights to optimize performance. The gradient is determined using a technique called back propagation, which involves performing computational backwards through the network.

In this paper, resilient back propagation training algorithm has been used. The algorithm Resilient Back-propagation (RPROP) is a local adaptive learning scheme, performing supervised batch learning in feedforward neural networks.

The following network depicts the multi-layer perceptron network which takes the input in the input layer X and categories the value into specific neuron in the output layer Z through the hidden layer Y.

Once the binary matrix has been acquired using tiles image, a processing procedure must be used in order to generate the input vector for the neural network. This procedure, called “features extraction”, aims to extract from the data the features which better highlight the differences between the two classes to be separated and, furthermore, to reduce the amount of data. The procedure here utilized is the following:

The image of the tiles has been acquired and generates the corresponding binary matrices of the tiles. The binary matrix is represented as 4x4 matrix which comprise of 0’s and 1’s combinations. Matrix values are passed as input vectors to the multilayer perceptron network. In this processing system, the matrix values of the perfect (non-defected) tile are passed to the network and update the weights of the neurons according to desired output. Then the matrices of the sample tiles are passing on to the network and checks whether the matrices are satisfied with output. If a matrix matches with the network output, that matrix is labeled as nondefected tile. Otherwise, the matrix is labeled as defected one. This process is implemented using back-propagation algorithm with random values to the initial neuron weights, threshold levels (θ), and learning rate (α).

The following graphs will illustrate the internal manipulations which are held in the perceptron network using back-propagation learning algorithm.

• VI.    Error Rate

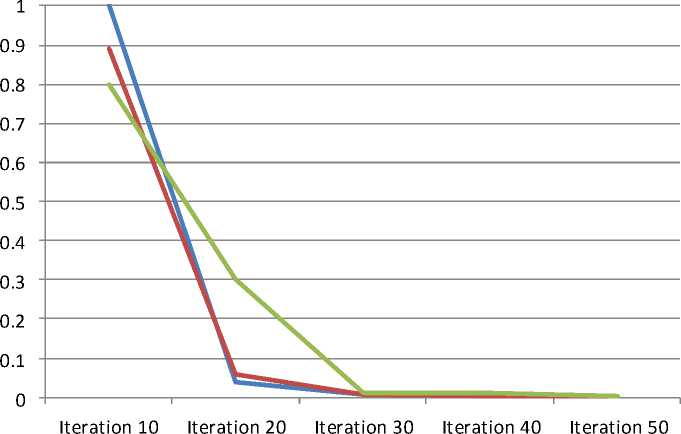
When the input is passing on to the network, it will be transform through the hidden layer to get the desired output. But the network will generate some output. Here if the actual output is not equal to the expected output, it will be considered as an error. The error rate will be calculate in each iteration by getting differences between actual and expected output which is represented in below graph.

	Product 1	Product 2	Product 3
Iteration 10	0.9998	0.8891	0.7988
Iteration 20	0.0376	0.0595	0.3015
Iteration 30	0.0064	0.0081	0.0108
Iteration 40	0.0025	0.0015	0.0096
Iteration 50	0.001	0.001	0.001

^^^^^w Product 1

^^^^^ Product 2

^^^^^m Product 3

• VII.    Weight Variation

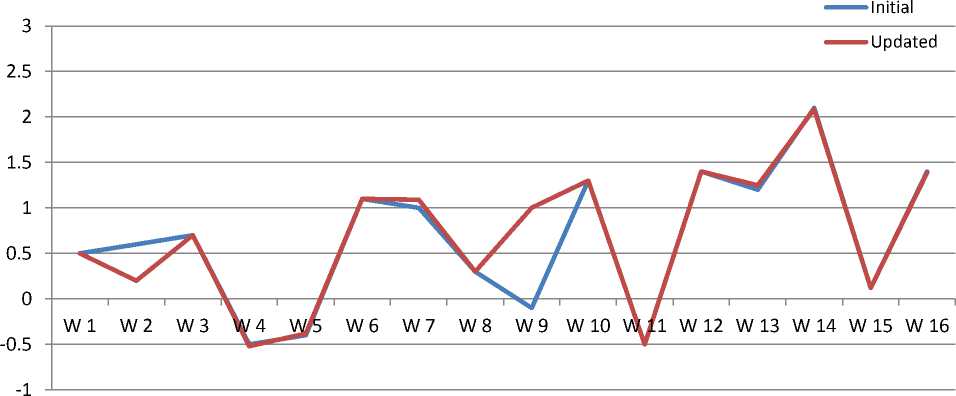
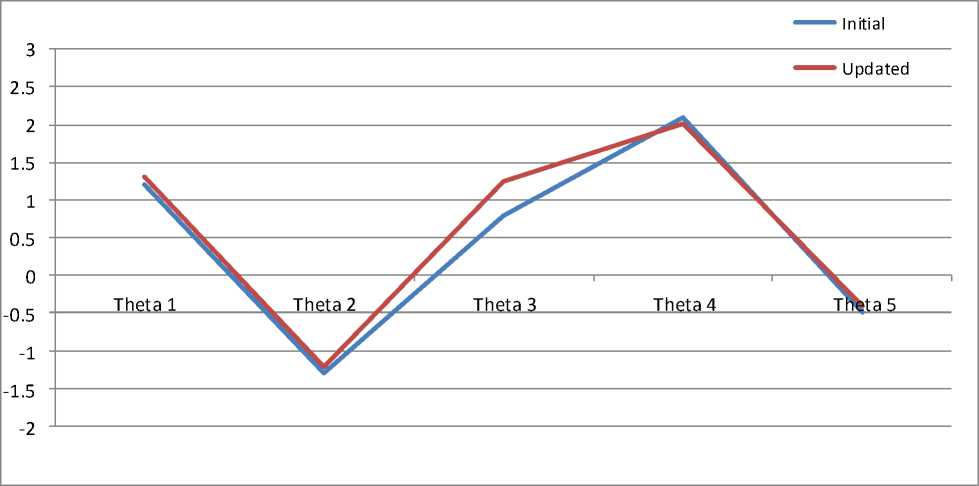
Initially, weights of the neurons (W) and the threshold levels (θ) are assigned randomly. When the to the network, the weight and threshold level will be updated according to the expected output. The initial and updated variations of the weight and threshold values are represented in following graphs.

	Initial	Updated
W 1	0.5	0.4999
W 2	0.6	0.2
W 3	0.7	0.6999
W 4	-0.5	-0.52
W 5	-0.4	-0.38
W 6	1.1	1.1
W 7	1	1.09
W 8	0.3	0.3
W 9	-0.1	1.002
W 10	1.3	1.2999
W 11	-0.5	-0.5
W 12	1.4	1.3999
W 13	1.2	1.25
W 14	2.1	2.086
W 15	0.12	0.1199
W 16	1.4	1.3888

	Initial	Updated
Theta 1	1.2	1.3
Theta 2	-1.3	-1.21
Theta 3	0.8	1.24
Theta 4	2.1	2.006
Theta 5	-0.5	-0.41

• VIII.    Conclusion

This paper is concerned with the problem of detection of the surface defects included on the fired ceramic tiles using the binary matrix value of images and Artificial Neural Network. The methodology is based on two steps: matrix measurements of the ceramic tile at no defected and defective; processing of the images for generating the input vector for the neural network