Деформации и прочность железобетонных балок, изготовленных из высокопрочного бетона при несовпадающих плоскостях температурного градиента и нагружения

Актуальность.

Температурные воздействия прикладываются к конструкциям, как правило, в форме температурных перепадов, что обусловливает проявление неоднородности прочностных и деформационных свойств бетона и арматуры в направлении теплового потока [1], [2], [3], а в статически неопределимых конструкциях - возникновение температурных усилий [1], [4], [5]. Трещинообразование, а также различия в величинах и в скоростях развития деформаций усадки и ползучести неравномерно нагретого бетона обусловливают изменение (релаксацию) Korsun, V.; Khon K.

температурных усилий в конструкциях с течением времени [4], [6], [7]. Случай несовпадения плоскостей нагрева и нагружения в железобетонных конструкциях является наиболее часто встречающимся, однако, он не рассмотрен в действующем СП 27.13330.2017 «Бетонные и железобетонные конструкции, предназначенные для работы в условиях воздействия повышенных и высоких температур» [8], ввиду малой изученности.

В ряде публикаций представлены результаты исследований влияния повышенных [1], [9], [10] и высоких температур уровня пожарной среды [11], [12], [13] на характеристики механических свойств обычных конструкционных [6], [14], [15] и высокопрочных [10], [13], [16] бетонов, а также бетонов с фибровым армированием [17], [18], [19]. В большинстве случаев [2], [20], [21] рассматриваются режимы кратковременного (до 240 минут) действия высоких (до 1000 т ) температур без учета длительных процессов в структуре бетоне, обусловленных деформациями усадки, ползучести и изменением характеристик физико-механических свойств бетона. При этом деформации усадки и ползучести бетона являются значимым фактором, который необходимо учитывать в задачах расчетной оценки НДС железобетонных конструкций [1], [22], [23]. Влияние режимов длительного нагрева на характеристики механических и реологических свойств бетонов в диапазоне повышенных до 200^О С температур изучено в недостаточной мере [11], [13], [24].

Экспериментальные исследования влияния нагрева на работу железобетонных элементов конструкций выполнены для образцов-балок [2], [19], [25] и плит [21], [26] преимущественно для диапазона высоких температур. Теоретические модели деформирования и остаточного сопротивления железобетонных конструкций после пожара выполнены в упрощенных вариантах без учета длительных процессов в бетоне и в арматуре [3], [5], [26].

Для конструкций промышленных зданий и сооружений, подвергающихся воздействиям повышенных технологических температур, характерны определенные режимы нагружения и нагрева, соответствующие этапам возведения, первого разогрева при вводе в эксплуатацию и последующей длительной эксплуатации объектов с возможными дополнительными силовыми и температурными нагружениями. Разработка и верификация методов расчетной оценки влияния режимов нагружения и нагрева на характеристики напряженно-деформированного состояния (НДС) железобетонных конструкций предполагает проведение экспериментальных исследований по специальным программам нагрева и нагружения.

Достоверная теоретическая оценка характеристик НДС неравномерно нагретых конструкций с учетом фактора времени и режимов нагружения и нагрева возможна на основе нелинейной деформационной модели, развиваемой в работах [1], [27] для случаев одно-, двух- и трехосных напряженных состояний. При этом основные соотношения указанной модели и ее вариантов нуждаются в проверке и в уточнении на основе сопоставления с результатами специально поставленных экспериментов.

Объект исследования – железобетонные элементы балочного типа. Предмет исследования – характеристики НДС железобетонных элементов при характерных режимах температурных и силовых воздействий.

Цель работы – экспериментальные и теоретические исследования НДС изгибаемых железобетонных элементов балочного типа из высокопрочного бетона при несовпадении плоскостей температурного перепада и нагружения, верификация определяющих соотношений нелинейной деформационной модели железобетона.

Задачи исследования:

• 1.    Выполнить экспериментальные исследования закономерностей изменения температурных усилий в статически неопределимых изгибаемых элементах балочного типа из высокопрочного бетона (ВПБ) и их деформаций в зависимости от температуры и продолжительности неравномерного нагрева.

• 2.    Исследовать экспериментальными методами деформации и несущую способность элементов конструкций из высокопрочного бетона при действии неравномерного нагрева и возрастающих до разрушения изгибающих моментов в несовпадающих плоскостях.

• 3.    Исследовать теоретическими методами влияние перепадов температуры в вертикальной и горизонтальной плоскостях и возрастающих изгибающих моментов в вертикальной плоскости на деформации и прочность конструкций балочного типа.

• 2    Materials and Methods

Экспериментальные исследования. Программа экспериментальных исследований включала два последовательных этапа испытания железобетонных образцов-балок: на первом этапе балки подвергались одностороннему нагреву снизу и сбоку до 60 Т и 90^о С при обеспечении неизгибаемости продольной оси. На втором этапе балки догружались изгибающим моментом M x в вертикальной плоскости до разрушения. Измеряемые величины: продольные деформации (удлинения) боковых граней балок на трех уровнях по высоте, прогибы в вертикальной плоскости, момент образования и ширина раскрытия трещин, предельные значения изгибающих моментов, соответствующих исчерпанию несущей способности конструкции. Устранение кривизны продольной оси балок от неравномерного нагрева осуществлялось на первом этапе испытаний путем приложения поперечных сил к их консолям, чем создавались изгибающие моменты, устраняющие свободную температурную кривизну, что соответствовало условиям работы в статически неопределимых конструкциях (рис.1).

a)

Рис. 1 – Схема (a) и иллюстрация (b) установки для испытаний балок при неравномерном нагреве и последующем догружении: 1 – опорная конструкция; 2 – тяги с резьбой; 3 – траверса; 4 – динамометры сжатия; 5 – кварцевые удлинители; 6 – индикаторы часового типа; 7 – термопары; 8 – нагревательные элементы; 9 – прогибометры; c) – схема устранения температурной кривизны балки при одностороннем нагреве

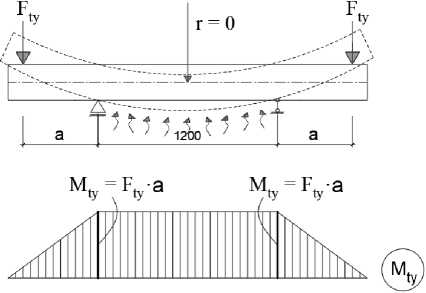
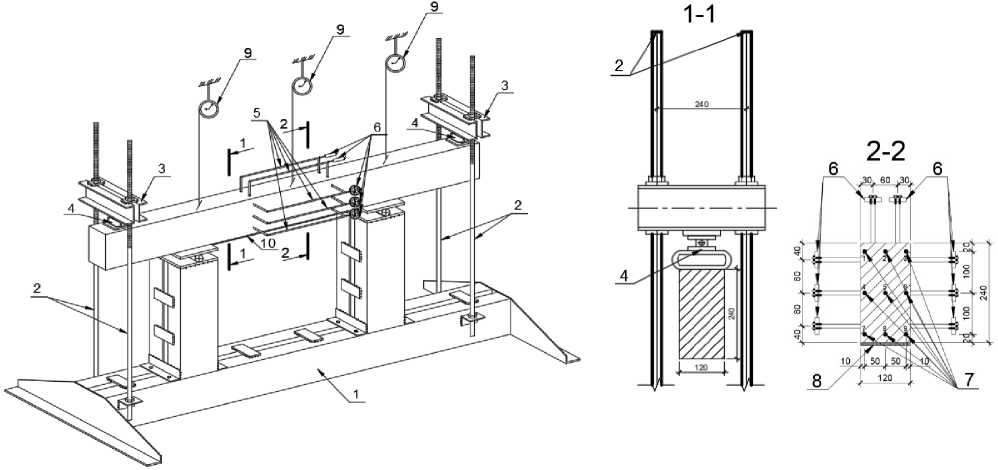
c)

Fig. 1 – Scheme (a) and illustration (b) of installation for beams' testing with uneven heating and subsequent reloading: 1 – structure's support; 2 – rods; 3 – traverse; 4 – compression dynamometers; 5 – quartz extension cords; 6 – hour-type indicators; 7 – thermocouples; 8 – heating elements; 9 – deflection meters; c) – scheme for eliminating the temperature curvature of the beam during unilateral heating

Опытные образцы - железобетонные балки из высокопрочного модифицированного бетона размерами 120×240х2400 (мм). Армирование в растянутой зоне – 2 ∅ 12 А500, в сжатой зоне – 2 ∅ 8 А500. За расчетное сопротивление арматуры принималось значение напряжения, соответствовавшего достижению состояния текучести в испытаниях на разрывной машине.

Бетон состава Ц:П:Щ = 1:1.61:1.73 с модификатором серии МБ-1 [28] в количестве 20% от массы цемента соответствовал классу по прочности В90. Цемент – портландский М500. Призменная прочность бетона в возрасте 28 суток - R b = (61.39 ^ 69.58) МПа.

Нагрев балок снизу и сбоку осуществлялся с помощью специальных электронагревательных элементов из нихромовой проволоки со скоростью подъема температуры 15 град.C в час. Распределение температуры по высоте и ширине сечения балок в зоне измерения деформаций определялось по показаниям хромель-копелевых (ХК) термопар.

За нагрузку достижения состояния текучести в арматуре растянутой зоны принималось значение изгибающего момента, при котором начинали наблюдаться существенные деформации (прогибы) образцов-балок без увеличения нагрузки, за критерий разрушения – раздробление бетона сжатой зоны.

• 3    Results and Discussion

Теоретические исследования НДС балок выполнены серией расчетов с применением нелинейной деформационной модели, реализованной в специально разработанной программе [27] расчета на основе физических соотношений, разработанных в [29], [30] применительно к обычному тяжелому бетону класса по прочности порядка В30. Применительно к высокопрочному бетону (ВПБ) в расчетную программу были внесены коррективы в части характеристик физикомеханических свойств ВПБ и их зависимости от кратковременного и длительного нагрева в диапазоне повышенных температур согласно данным [10], [31]. Закономерности проявления температурно-усадочных деформаций и ползучести ВПБ моделировались согласно методикам [29], [30]. Верификация модифицированных физических соотношений для бетона, реализованных в программе расчета, выполнена сопоставлением расчетных характеристик напряженно-деформированного состояния с данными опытов на образцах-балках [1], [4], [6].

Распределение температуры по высоте и ширине сечения принималось заданным и равным значениям, полученным в опытах [1], [4] по показаниям ХК-термопар.

Неоднородность свойств бетона и арматуры по высоте и ширине сечения учитывалась путем представления поперечного сечения железобетонного элемента в виде системы условно однородных участков бетона и отдельных стержней арматуры [1], [27]. При этом напряжения, а также характеристики физико-механических свойств бетона и арматуры принимались постоянными по всей площади элементарного сечения соответственно температуре нагрева и уровню напряженного состояния. Применен раздельный учет физической нелинейности деформирования и длительных процессов в бетоне, что позволяет моделировать в расчетах конструкций режимы длительных температурных воздействий эксплуатационного уровня и кратковременных нагружений возрастающей нагрузкой.

За критерии исчерпания прочности принимались: для участков бетонного сечения в растянутой зоне – достижение напряжениями значений предела прочности на растяжение R bt (t ^o ,T); для участков в бетоне сжатой зоны – достижение бетоном деформаций, равных 1,4 от предельных значений в вершине диаграммы. Расчетная диаграмма деформирования для бетона принималась криволинейной в форме известной диаграммы Сарджина. Параметры диаграммы задавались по результатам экспериментальных исследований [10], [30], [31].

Диаграмма деформирования арматуры – двухлинейная в форме диаграммы Прандтля. Значения напряжений в арматуре, соответствующих пределу текучести, были определены путем испытаний арматурных стержней и составили, в среднем, R s = 776,2 МПа.

Работа железобетона с трещинами описывалась в рамках модели В.И. Мурашева с помощью коэффициента ψ s по модифицированным выражениям [27].

Korsun, V.; Khon K.

Strains and strength of reinforced concrete beams manufacturing by high-strength concrete for non-coincident planes of temperature gradient and loading;

Система разрешающих уравнений равновесия внешних сил Mx, My, Nz и внутренних усилий сопротивления в нормальных сечениях железобетонных элементов балочного типа в компактной матричной форме принята в виде [27]:

м x		A 1	B 1	C 1		Х Х		м OX
м y	=	A 2	B 2	C 2	*	X Y	+	м OY	,                                       (1)
N z		A 3	B 3	C 3		£ OZ		N OZ

• где: A 1 , …..A 3 - коэффициенты матрицы жесткости;

• ε oz , ϰ x , ϰ y - соответственно продольные относительные деформации элемента на уровне срединной оси и кривизны оси балки относительно координатных осей X и Y;

Mox , Moy , Noz - элементы свободного вектора-столбца, обусловленные влиянием температурных деформаций и ползучести в расчетных элементах бетона и арматуры.

Выражения для коэффициентов матрицы жесткости и элементов свободного вектора-столбца приняты согласно работе [27].

Исходные характеристики физико-механических свойств высокопрочного бетона исследованного состава и их зависимость от режимов температурных и силовых воздействий принимались по данным исследований [4], [10], [31].

Решение физически нелинейной задачи осуществлялось методом упругих решений в сочетании с шаговым методом приращения температурной и силовой нагрузки. Процесс нагружения элементов конструкций разбивался на ряд этапов приращения температуры и изгибающих моментов M x . Секущие модули деформаций бетона и арматуры принимались для каждого элементарного участка в каждом приближении величинами постоянными и равными значениям, определенным на предыдущей итерации. Наличие или отсутствие трещин определялось отдельно для каждого рассматриваемого элементарного участка бетона на каждой итерации расчета. После образования трещин или разрушения элементарных участков бетона значения их модулей деформаций принимались равными нулю.

Результаты экспериментальных и теоретических исследований. В экспериментальных исследованиях [1], [4] моделировались случаи несовпадения плоскостей нагрева и нагружения, характерные для ситуаций с односторонним нагревом конструкций солнцем, нагревом от тепловых агрегатов и др. Такое сочетание воздействий обусловливает возникновения в статически неопределимых конструкциях сложной формы изгиба – косого изгиба.

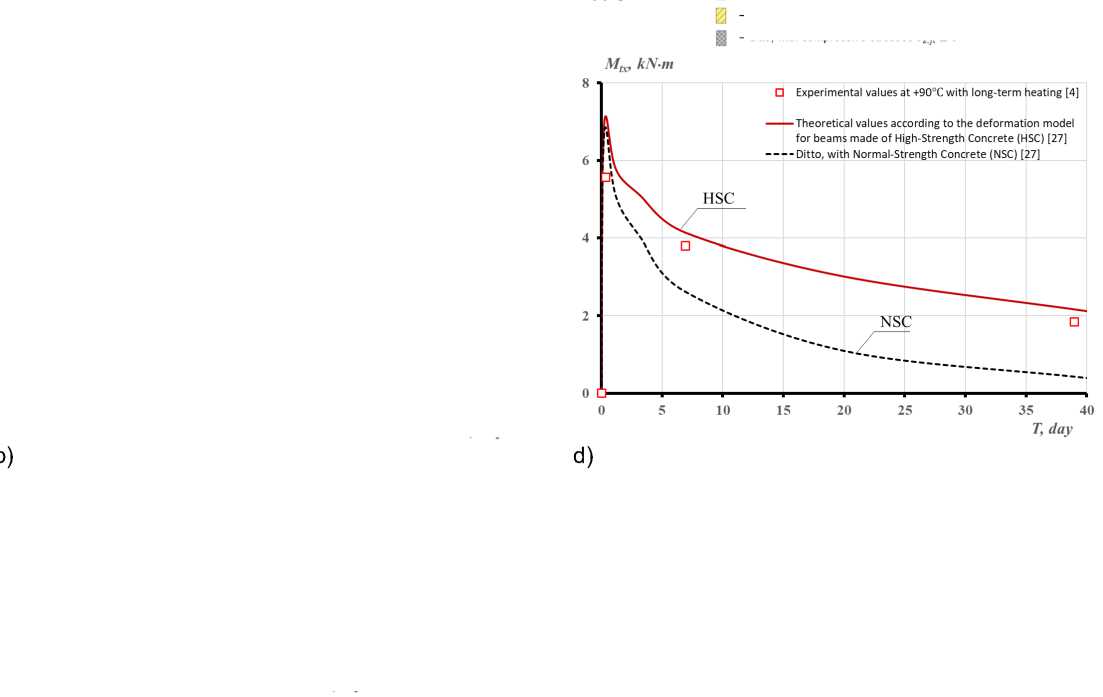
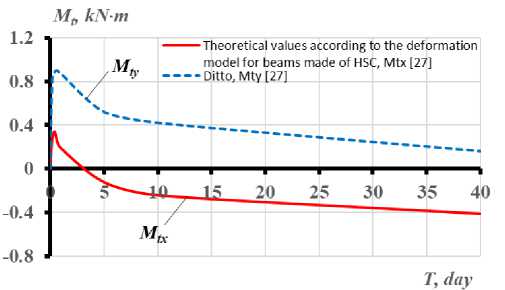
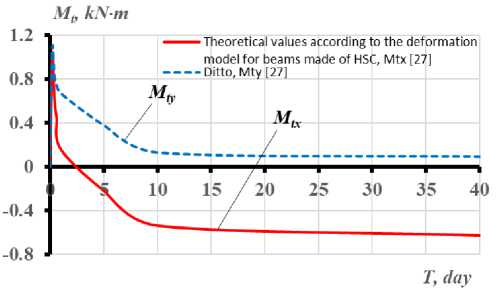
Сопоставление результатов расчетов с опытными данными (рис. 2–4) свидетельствует о превышении расчетными по методике [27] температурными моментами опытных величин [4] не более, чем на 10%. При этом величины температурных моментов возрастают на этапе разогрева конструкций пропорционально увеличению температурного перепада по высоте и ширине сечения. Максимальные их величины соответствуют моменту трещинообразования в растянутой, менее нагретой зоне балки. Через 42 час от начала нагрева наблюдается изменение знака температурного момента на противоположный, а затем, после 106 час от начала нагрева -повторное изменение знака изгибающего момента, характеризующее появление растягивающих напряжений на менее нагретой грани.

Подобная особенность изменения температурных моментов отмечена также в работах [1], [4] на примерах элементов в виде не изгибаемых балок и пластин и обусловлена разными скоростями развития деформаций усадки и ползучести бетона в более и менее нагретых зонах неравномерно нагретых элементов.

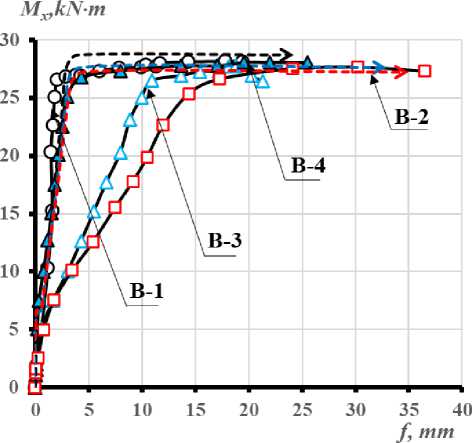
При последующем догружении односторонне нагретой до + 90 ° С балки возрастающим изгибающим моментом ΔM = ΔF∙a (схема - на рис. 5b) величина опытного разрушающего изгибающего момента оказалась практически равной несущей способности эталонной, предварительно не нагревавшейся балки (рис. 5a), испытанной по такой же схеме нагружения в условиях нормальной температуры. При этом подвергавшаяся неравномерному нагреву балка получила более высокие величины прогибов, что связано с большими пластическими деформациями бетона вследствие снижения его модуля упругости и повышения предельной сжимаемости бетона в условиях нагрева.

Теоретическое определение величин напряжений по методике [1], [27] и последовательности их изменений в нормальных сечениях неоднородных железобетонных балочных элементов из ВПБ при различных вариантах их нагрева снизу и сбоку представлены на рисунках 6 и 7. Результаты расчетов отражают реализацию сложной формы изгиба – косого

момента в

изгиба, которая приближается к плоскому изгибу по мере возрастания изгибающего вертикальной плоскости.

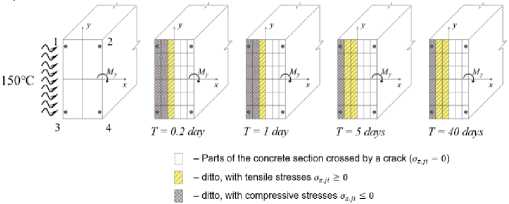
- ditto, with tensile stresses o_zii >  0

- ditto, with compressive stresses o_{x ji} < 0

- ditto, with tensile stresses tr_zi, > 0

- ditto, with compressive stresses o2 J! < 0

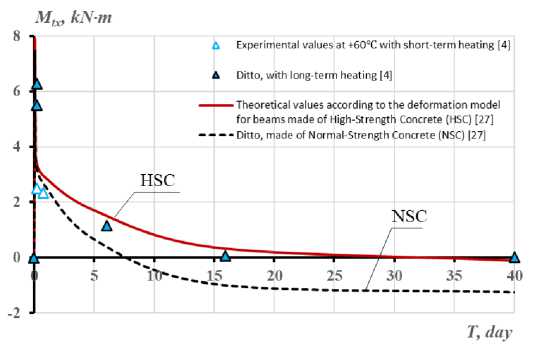
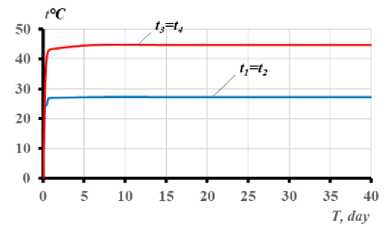
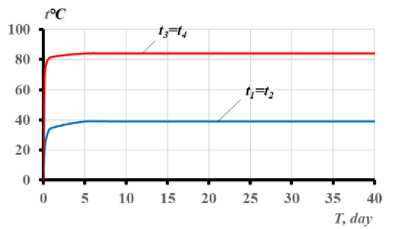
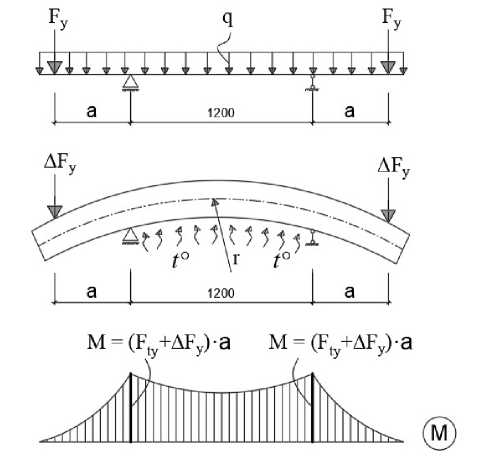
Рис. 2 - Изменение температурных моментов M _tx , схемы развития трещин и перемещений границ сжатой и растянутой частей бетонного сечения балки при длительном неравномерном нагреве в течение 40 суток: а) - при одностороннем нагреве снизу до +60° С ; с) - при одностороннем нагреве снизу до +90 С ; b, d) - графики опытных значений температур в угловых точках сечений

Fig. 2 - The change of temperature moments M _tx , schemes of crack development and boundaries' displacements of compressed and stretched parts of the concrete section of the beam with prolonged uneven heating for 40 days: a) – with unilateral heating from the bottom up to +60 С ; с) - with unilateral heating from the bottom up to +90 С ; b, d) - experimental graphs of temperature values at the sections' angular points

a)

90°C

60°C

I

- Parts of the concrete section crossed by a crack (а2/( = 0)

- ditto, with tensile stresses a_2fl > 0

- ditto, with compressive stresses a_Iit<  0

Q - Parts of the concrete section crossed by a crack (az^ = o)

- ditto, with tensile stresses а_г,_{1 > 0

- ditto, with compressive stresses а_г)1 < 0

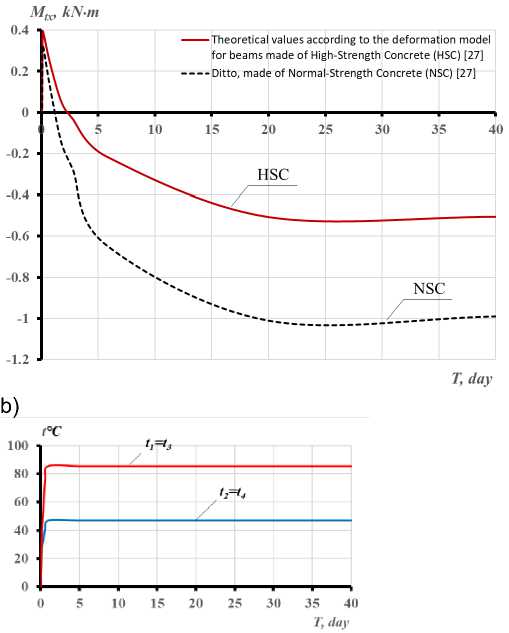
Рис. 3 - Изменение температурных моментов M _tx , M _ty , схемы развития трещин и перемещений границ сжатой и растянутой частей бетонного сечения балки при длительном неравномерном нагреве в течение 40 суток: а) - при одностороннем нагреве сбоку до +90° С ; с) - при одновременном нагреве сбоку до +90 С и снизу до +60 С ; b, d) - графики опытных значений температур в угловых точках сечений

Fig. 3 - The change of temperature moments M _tx , M _ty , schemes of crack development and boundaries' displacements of compressed and stretched parts of the concrete section of the beam with prolonged uneven heating for 40 days: a) – with unilateral heating from the side up to +90 С ; c) - with simultaneous heating from the side up to +90 С and from the bottom up to +60° С ; b, d) – experimental graphs of temperature values at the sections' angular points

d)

b)

d)

T, day

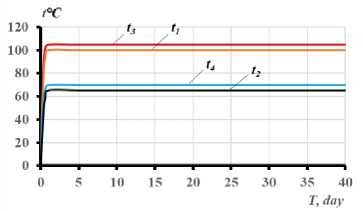
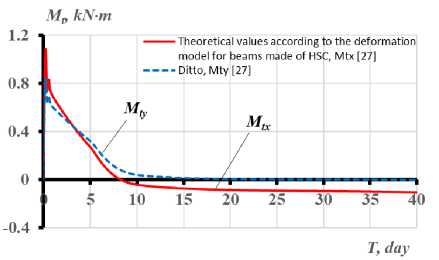
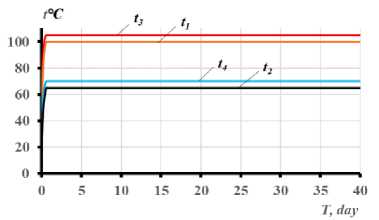
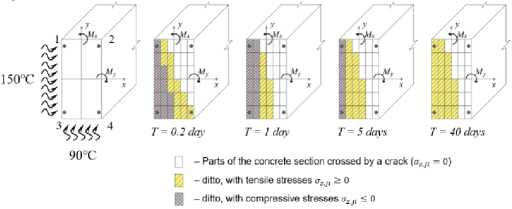
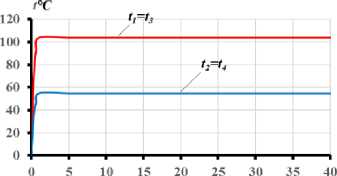
Рис. 4 - Изменение температурных моментов M _tx , M _ty , схемы развития трещин и перемещений границ сжатой и растянутой частей бетонного сечения балки при длительном неравномерном нагреве в течение 40 суток: a) – при одностороннем нагреве сбоку до +150 Т ; с) - при одновременном нагреве сбоку до +150 С и снизу до +90^о С; b, d) - графики опытных значений температур в угловых точках сечений

Fig. 4 - The change of temperature moments M _tx , M _ty , schemes of crack development and boundaries' displacements of compressed and stretched parts of the concrete section of the beam with prolonged uneven heating for 40 days: a) – with unilateral heating from the side up to +150° С ; c) - with simultaneous heating from the side up to +150 С and from the bottom up to +90 С ; b, d) - experimental graphs of temperature values at the sections' angular points

a)

—O— Experimental values at one-sided heating of temperatures 20°C [4]

й Ditto, 60°C under short-term heating [4]

b)

—й— Ditto, 60°C under long-term heating [4]

^^ Ditto, 90°C under short-term heating [4]

--^ Theoretical values according to the deformation model for beams made of HSC at temperatures of 20°C [27]

--^ Ditto, 60°C under short-term heating [27]

— — ^ Ditto, 90°C under short-term heating [27]

Рис. 5 – Изменение прогибов (a) и схема деформирования балок (b) из высокопрочного бетона при догружении изгибающим моментом Mx в вертикальной плоскости

Fig. 5 – The change of beams' deflections (a) and deformation scheme (b) manufacturing by high- strength concrete with loading by bending moment Mx in the vertical plane

4 Conclusions

• 1.    Температурные моменты в односторонне нагреваемых железобетонных балках возрастают пропорционально величине температурного перепада, достигают максимального значения при первом нагреве и снижаются после образования трещин.

• 2.    Прочность железобетонной балки из ВПБ на изгиб в условиях одностороннего нагрева при 90 С в течение 10 суток близка к значению прочности не нагревавшейся эталонной балки. Это связано с меньшей чувствительностью высокопрочного бетона к действию повышенных температур в диапазоне до +90 С .

• 3.    Результаты расчетов с использованием соотношений нелинейной деформационной модели достаточно близко соответствуют опытным данным для характерных режимов нагружения и неравномерного нагрева.

• 4.    Точность оценки характеристик НДС железобетонных элементов-балок при неравномерном нагреве и нагружении существенно зависит от точности моделирования в расчете закономерностей изменения с течением времени деформационных и прочностных свойств, температурно-усадочных деформаций и деформаций ползучести ВПБ при воздействии повышенных температур.

• 5.    Близкие соответствия расчетных величин по нелинейной деформационной модели опытным в части температурных моментов, деформаций (прогибов) элементов балочного типа (элементов-балок) и их несущей способности при изгибе свидетельствует о достаточной точности примененной методики нелинейного расчета к конструкциям из ВПБ.

• 6.    Наиболее важными факторами, влияющими на напряженно-деформированное состояние железобетонных конструкций при совместном воздействии температурных градиентов и нагрузки, являются зависимость деформационных и прочностных свойств бетона от температуры и продолжительности ее действия, неоднородность силовых, температурно-усадочных деформаций и ползучести бетона, трещинообразование.

Максимальные опытные значения температурных моментов при одностороннем нагреве балок до +90^о С составили около 20% от их несущей способности.

а)

b)

c)

60°С

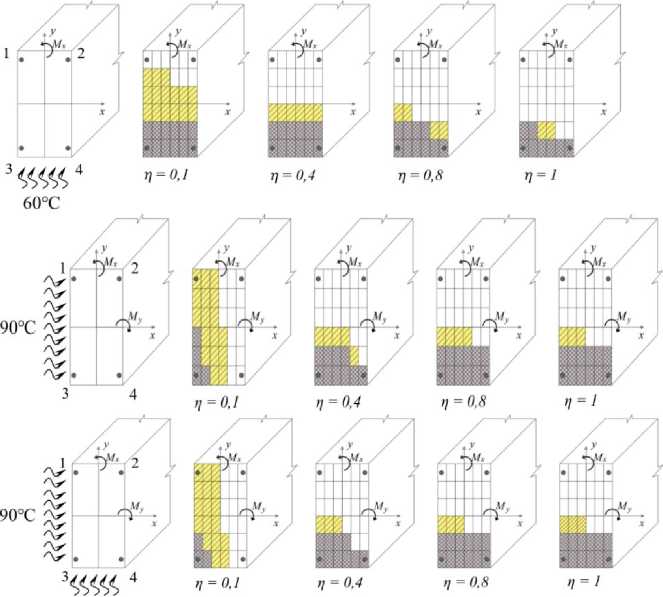
Рис. 6 – Схемы развития трещин и перемещений границ сжатой и растянутой частей бетонного сечения балки при её догружении возрастающим изгибающим моментом М _х до уровней q = М _х /М _х,_и после длительного неравномерного нагрева в течение 40 суток: а) -односторонний нагрев снизу до +60° С ; b) - односторонний нагрев сбоку до +90 С ; с) -двухсторонний нагрев сбоку до +90° С и снизу до +60 С

Fig. 6 – Schemes of crack development and boundaries' displacements of compressed and stretched parts of the concrete section of the beam with loading by increasing bending moment q = Мх/Мхи after prolonged uneven heating for 40 days: а) - unilateral heating from the bottom up to +60T; b) - unilateral heating from the side up to +90^; c) - double-sided heating from the side up to +90С and from the bottom up to +60С

a)

b)

c)

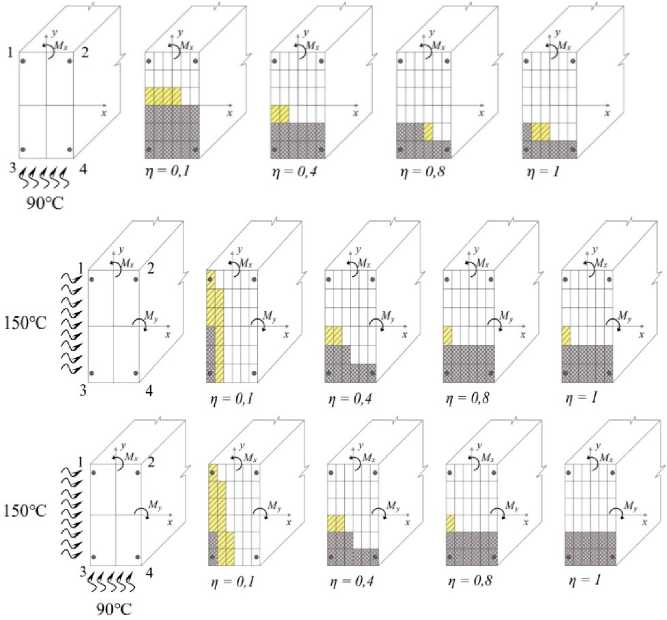
Рис. 7 – Схемы развития трещин и перемещений границ сжатой и растянутой частей бетонного сечения балки при её догружении возрастающим изгибающим моментом М _х до уровней q = M _x /M _xu после длительного нагрева в течение 40 суток: a) - односторонний нагрев снизу до +90° С ; b) - односторонний нагрев сбоку до +150° С ; с) - двухсторонний нагрев сбоку до +150° С и снизу до +90° С

Fig. 7 – Schemes of crack development and boundaries' displacements of compressed and stretched parts of the concrete section of the beam with loading by increasing bending moment q = M _x /M _x,_u after prolonged uneven heating for 40 days: а) - unilateral heating from the bottom up to +90° С ; b) - unilateral heating from the side up to +150 С ; c) - double-sided heating from the side up to +150 С and from the bottom up to +90 С