Деформации как метод управления уровнями дефекта в теллуриде кадмия. 1. Дефект замещения с нулевым зарядом

ВВЕДЕНИЕ                          МЕТОД РАСЧЕТА

Теллурид кадмия является одним из самых распространенных полупроводниковых материалов для регистрации радиоактивного излучения. Благодаря высокому атомному номеру элементов, входящих в состав соединения, и широкой запрещенной зоне этого полупроводника детекторы на его основе обладают высокой эффективностью регистрации и энергетическим разрешением и могут, в отличие от кремниевых и германиевых детекторов, работать при комнатной температуре [1– 3].

Дальнейшему улучшению спектрометрических характеристик детекторов препятствуют образующиеся при синтезе кристаллов дефекты и примеси. Одним из наиболее проблемных дефектов является собственный дефект замещения TeCd, который возникает при замещении атома кадмия атомом теллура в кристаллической решетке полупроводника и может находиться в различных зарядовых состояниях.

Исследования, проведенные ранее в работах [4– 8], позиционируют этот дефект в основном как глубокий донор, но однозначно определить его энергию не удается.

В настоящей работе представлены результаты, проведенных нами расчетов энергетического уровня дефекта для случая нейтрального зарядового состояния Te⁰ Cd . Определена его геометрия, а также установлены закономерности влияния трех типов деформаций на положение энергетического уровня Te Cd в запрещенной зоне полупроводника.

Наиболее удобным и распространенным способом моделирования дефекта в кристаллической решетке является кластерное моделирование, или моделирование дефекта в сверхъячейке [9]. В данной работе с этой целью используется программный пакет VASP (Vienna Ab-initio Simulation Package) [10], базирующийся на принципах теории плотностей функционалов. Расчеты проводились в приближении локальных плотностей LDA (Local Density Approximation) [11, 12] с параметризацией Сеперли—Алдера (CA) [13].

Нами была сконструирована 128-атомная гранецентрированная сверхъячейка теллурида кадмия. Для валентных электронов кадмия применялась конфигурация 4d¹⁰5s², а для теллура — 5s²5p⁴. Волновые функции валентных электронов представлены в базисе плоских волн с энергией отсечки в 500 эВ. Для разрешения зоны Бриллюэна были взяты распределения k -точек 2×2×2 и 6×6×6 и при проведении расчетов учитывалось гауссовское уширение в 0.05 эВ.

Анионный дефект замещения моделировался заменой одного из атомов кадмия атомом теллура в 128-атомной сверхъячейке теллурида кадмия.

Деформации модели были представлены варьированием значения постоянной решетки а теллурида кадмия в одном, двух и трех кристаллографических направлениях (рис. 1).

Основными принципами создания качественной виртуальной модели, с одной стороны, является степень сходства моделируемых параметров

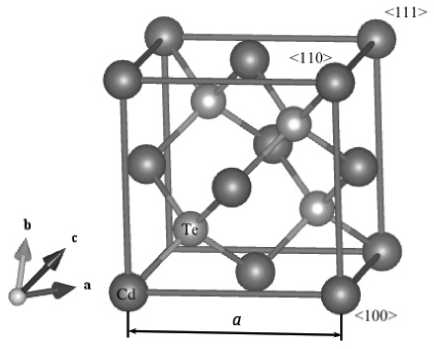
Рис. 1. Кристаллическая решетка теллурида кадмия (CdTe).

a , b , c — векторы примитивной решетки, направленные вдоль <110>; a — параметр решетки

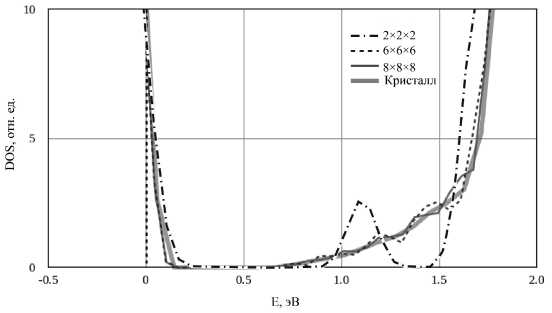
Рис. 2. Электронные плотности состояний 128-атомной сверхъячейки теллурида кадмия, рассчитанные при 2×2×2 (штрих-пунктирная линия), 6×6×6 (пунктирная линия) и 8×8×8 (тонкая серая сплошная) распределениях k -точек в сравнении с идеальным кристаллом теллурида кадмия (черная толстая сплошная линия)

со свойствами реального образца, с другой — минимизация затрат компьютерных ресурсов. Для вычисления оптимальных параметров модели, представленной в данной работе, проводился ряд предварительных вычислений.

Минимально возможная концентрация дефектов, получаемая при синтезе кристаллов теллурида кадмия в настоящее время, очень мала и составляет величину порядка 1012 см–3 [16]. Чтобы точно воспроизвести такую концентрацию дефекта необходимо использовать сверхъячейку размером приблизительно в 32·109 атомов, что требует огромных вычислительных затрат и в рамках программного пакета VASP представляется на сегодняшний день невозможным.

Однако для решения поставленной задачи достаточно использовать такое количество атомов в сверхъячейке, которое позволит в необходимой мере изолировать атомы дефекта друг от друга. Так, например, при использовании 54-атомной сверхъячейки атомы замещения "чувствуют" друг друга, что выражается в значительной дисперсии их энергетического спектра. Это весьма затрудняет анализ, поскольку такой результат сильно расходится с реальным положением вещей. При использовании 128-атомной сверхъячейки дисперсия наблюдается в гораздо меньшей степени.

Другой не менее важный параметр — набор и распределение k-точек в зоне Бриллюэна. Перед выполнением основных расчетов были протестированы три различных варианта — 2x2x2, 6x6x6 и 8x8x8 к-точек, результаты которых представлены на рис. 2. В качестве эталона была взята электронная плотность состояний теллурида кадмия, рас- считанная с использованием 2-атомной ячейки. Как видно из рисунка, для эффективного разрешения недостаточно набора 2x2x2 к-точек, т. к. вблизи потолка зоны проводимости в этом случае образуется неоправданный всплеск электронной плотности состояний. Распределения 6x6x6 и 8x8x8 приводят к близким значениям, но набор из 8x8x8 к-точек требует гораздо больше временных и компьютерных затрат.

Таким образом, можно сделать вывод, что наиболее удобной моделью в нашем случае является 128-атомная сверхъячейка теллурида кадмия с набором к -точек 6 x 6 x 6. В некоторых случаях, где плотность состояний и зонная структура не являются приоритетной информацией, для ускорения сходимости расчетов нами использовалось распределение к -точек 2 x 2 x 2.

Энергии дефектообразования рассчитывались для условий Cd- и Te-насыщенных газовых фаз. Выражение, используемое для расчета энергии дефектообразования Δ H_f , имеет вид

N H f =^ E - ^ n i M i , (1)

где Δ E — разность в энергиях идеальной сверхъячейки и сверхъячейки с дефектом; μ — относительный химический потенциал атомов каждого типа; n — разница в количестве атомов каждого типа между идеальной и содержащей дефект сверхъячейки . В данном случае n Cd = – 1 (на один кадмий меньше, чем в идеальной сверхъячейке) и соответственно n Te = 1. В итоге для расчета энергии дефектообразования Te⁰ Cd формула (1) преобразуется в (2):

N H f =N E - ^ те + ^.          (2)

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Недеформированный дефект замещения

Как было отмечено выше, дефект образуется при замещении атома кадмия атомом теллура в узле кристаллической решетки. Но у данного дефекта есть свои особенности, основным из которых является свойство понижения симметрии в результате ян-теллеровского искажения. Если взять идеальную решетку теллурида кадмия, которая обладает симметрией T d и заменить один из атомов кадмия теллуром, и позволить данной структуре оптимизировать геометрическую конфигурацию в соответствии с минимальной энергией, то можно отметить, что атом замещения (Te Cd ) не останется ровно на том же месте, где находился

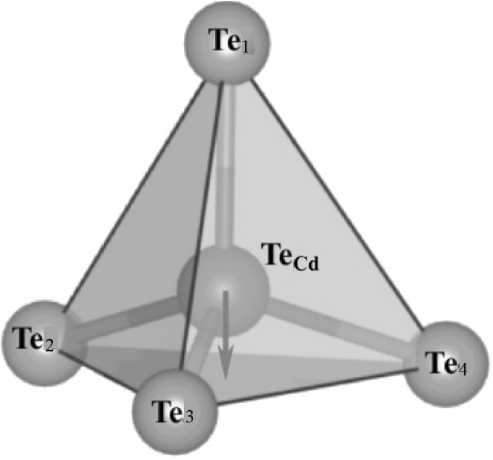
Рис. 3. Положение дефекта замещения

"родной" кадмий. Он немного сдвинется в одном из кристаллографических направлений <111>, понижая локальную симметрию до C 3v (рис. 3). На рис. 3 показан переход от симметрии T d к C 3v при смещении центрального атома (Te Cd ) в одну из плоскостей тетраэдра, образованного ближайшими "соседями" (Te 1 , Te 2 , Te 3 и Te 4 ). Изменение параметров приведено в табл. 1.

Подобную конфигурацию можно объяснить, исходя из электронной структуры атомов кадмия и теллура. Так как соединение CdTe принадлежит группе полупроводников типа АIIBVI, можно определить, что кадмий обладает валентностью II, а теллур четырехвалентен. Тип кубической гранецентрированной решетки предполагает, что каждый атом теллура окружен четырьмя атомами кадмия и наоборот. Таким образом, если равномерно распределить валентные электроны, то на каждую атомную связь приходится по два электрона. Это обусловливает высокую симметрию T d идеальной решетки CdTe и sp ³-гибридизацию внешних электронных оболочек. Далее, если заменить один из атомов кадмия теллуром, получится, что в данном узле будет 12 валентных электронов вместо восьми. Такой электронный дисбаланс приводит к образованию трех полноценных связей, но разрушает четвертую, образуя так называемое состояние "отталкивания" [5].

На рис. 4 изображены энергетические диаграммы, относящиеся к T d - и C 3v -симметриям. Для случая симметрии третьего порядка представлена заполненность уровней 12 электронами, как это происходит в случае с дефектом замещения. Здесь распределение электронов происходит совершенно по-иному, чем в идеальном теллуриде кадмия. В первую очередь связи образуются между атомом замещения Te Cd и его тремя ближайшими соседями (Te 2 , Te 3 и Te 4 ) (рис. 3), переходя из sp ³- в sp ²-гибридизацию. В образовании этих связей участвуют электроны, находящиеся на 1A 1 ^b , 1A 1 ^a и E ^b

Табл. 1. Сравнение основных параметров 128-атомных сверхъячеек CdTe и CdTe c Te⁰ Cd

Сверхъячейка	Параметр	Настоящая работа	Литературные данные	Эксперимент
CdTe	Параметр решетки a , Å	6.420	6.447 [11], 6.420[9]	6.48 [12]
	Ширина зоны, эВ	0.64	0.6 [11]	1.56 [12]
	d (Te Cd – Te 1 ), Å	3.581	3.59 [11]	—
CdTe с Te0 Cd	d (Te Cd – Te 2 ), Å	2.905	2.93 [11], 2.91 [9]	—
	Z Te i Te cd Te 2	90.4º	—	—
	Z Te 2 Te cd Te 3	120.0º	—	—

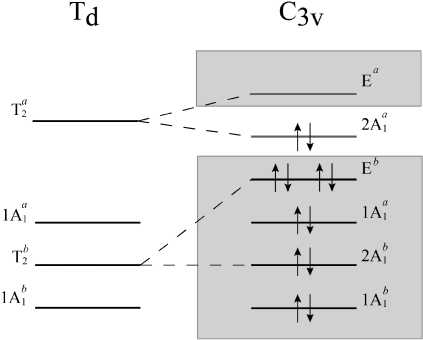
Рис. 4. Энергетические диаграммы дефекта замещения Te Cd

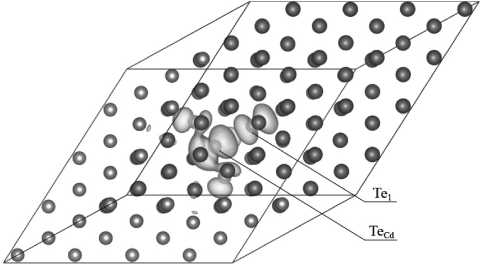
Рис. 5. Изоповерхность плотности заряда, относящейся к уровню 2А₁ в недеформированной решетке CdTe

E , эВ

а

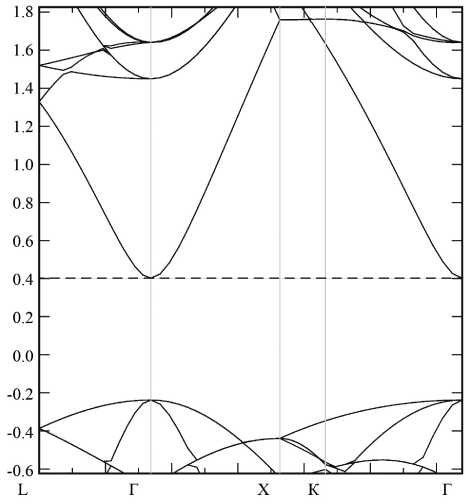
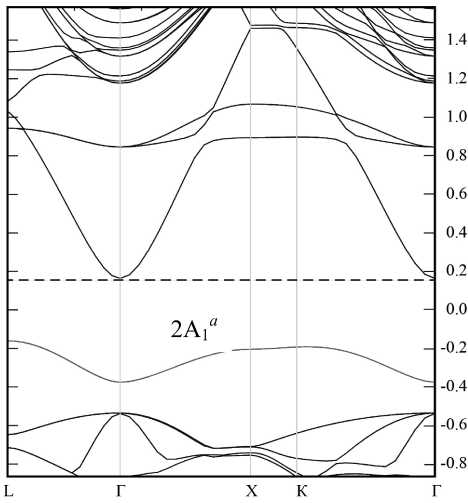
Рис. 6. Зонные структуры идеальной кристаллической решетки теллурида кадмия (а) и теллурида кадмия с дефектом замещения (б).

2А₁ ^a — энергетический уровень в запрещенной зоне, принадлежащий дефекту замещения

б

E , эВ

энергетических уровнях (рис. 4). Четвертый атом, Te1, не участвует в формировании связей с атомом замещения, поскольку связывающие T2b уровни, ранее отвечавшие за эту связь, теперь расщеплены на два уровня 2А1b и Еb. Уровень Eb с px- и py-подобными орбиталями относится к атомам TeCd, Te2, Te3 и Te4, а уровень 2А1b трансформируется из pz-подобной орбитали в s-подобную и участвует только в образовании связей Te1 с ближайшими тремя атомами кадмия. На долю Te1 – TeCd приходятся оставшиеся отталкивающие состояния 2A1a и Ea, из которых Ea не заполнен, а 2A1a , в котором участвуют главным образом pz-орбитали Te1 и TeCd атомов, увеличивает их расхождение. На рис. 5 показана зарядовая изоповерхность 2A1a уровня в сверхъячейке из 128 атомов.

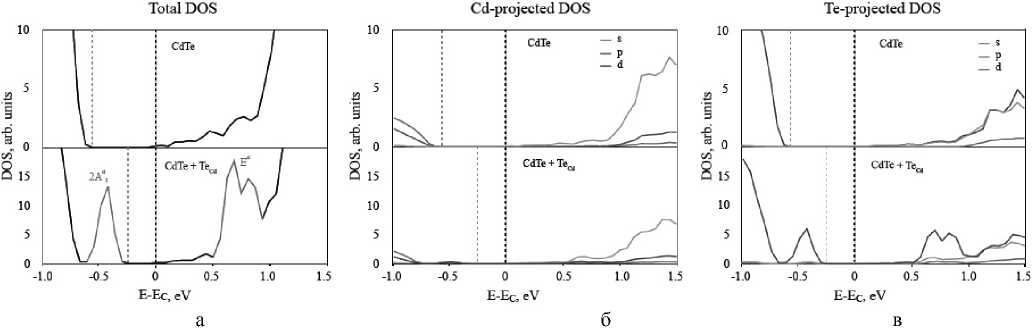
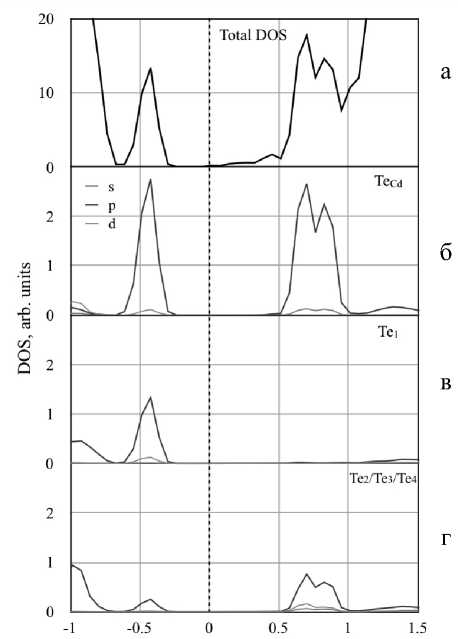
Рис. 7. Электронная плотность состояний идеального TeCd и с дефектом замещения (а) верхний и нижний рисунки соответственно, а также отдельные электронные плотности состояний кадмия (б) и теллура (в)

E-Ec, eV

Рис. 8. Электронная плотность состояний TeCd с дефектом замещения (а), отдельные электронные плотности состояний атома замещения (б), его дальнего соседа Te 1 (в), а также ближайших трех эквивалентных атомов Te 2–4 (г)

Кроме того, из рис. 4 видно, что при заполнении энергетических уровней с T d - симметрией 12 электронами^*) верхний заполненный уровень будет находиться выше, чем при С 3v -симметрии, поэтому С 3v -симметрия является более предпочтительной для данной конфигурации.

Как было показано выше, дефект замещения Te_Cd образует шесть энергетических уровней, один из которых (2A 1 ^a ) попадает в запрещенную зону полупроводника. Это видно из схематической энергетической диаграммы (рис. 4), зонной структуры, представленной на рис. 6, б, а также из графиков плотности состояний (рис. 7, 8) и (Приложение). Конкретные значения положения этого уровня дефекта приведены в табл. 2. В таблице показаны экспериментальные, теоретические и полученные в данной работе значения положения уровня 2A 1 ^a в запрещенной зоне относительно потолка валентной зоны ( E_v ) или дна зоны проводимости ( E с ). Значения, полученные в настоящей работе, приведены относительно потолка валентной зоны, т. к. метод приближения локальной плотности не позволяет точно рассчитать положение дна зоны проводимости.

Для анализа вклада ближайших атомов кадмия в общую энергетическую картину дефекта были проведены расчеты плотностей состояний отдельно для атомов кадмия и теллура. На рис. 7, а, показаны суммарные плотности электронных состояний для идеальной решетки теллурида кадмия (вверху) и для решетки с дефектом (внизу). На рис. 7, б, представлены соответственно плотности состояний для атомов кадмия, входящих в состав суперъячейки, и для атомов теллура для идеальной решетки и решетки с дефектом. Как несложно заметить,

^*) На T 2 уровень приходится 6 электронов.

Табл. 2. Энергии уровня дефекта в CdTe

Энергия уровня дефекта, эВ	Литература	Примечание
E v + 0.16…0.35 E v + 0.4 E с – 0.6 ( E v + 0.96) E с – 0.86 ( E v + 0.7) E с – 0.75…0.83 ( E v + 0.81…0.73) E с – 0.8…1.05 ( E v + 0.76…0.51) E с – 0.69…0.71 ( E v + 0.87…0.85) E с – 0.79 ( E v + 0.77)	Настоящая работа [9] [2] [2] [3] [3] [13] [13]	128-атомная ячейка 64-атомная ячейка Фотопроводимость при температурах 300 и 65 К Фотопроводимость при температурах 300 и 65 К — — — —

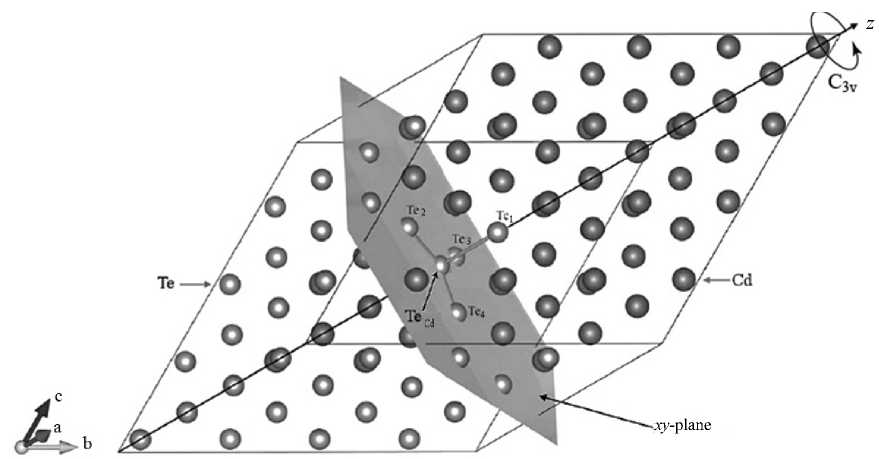
z xy-plane

Рис. 9. Расположение 128-атомной ячейки CdTe в соответствии с адаптированной под деформации системой координат

атомы кадмия практически не вносят вклад в образование дефекта (лишь небольшая плотность состояний наблюдается в районе пика 2А 1 ^а ), в то время как теллур практически полностью формирует оба пика, принадлежащие дефекту (рис. 7, в). Также следует обратить внимание, что в формировании уровней участвуют преимущественно p- электроны.

Теперь, поскольку из расчетов следует, что кадмий практически не участвует в образовании интересующих нас уровней дефекта, можно оценить вклад каждого из пяти упомянутых ранее атомов теллура. На рис. 8 приведены составляющие плотности состояний для каждого из пяти атомов теллура. Из рисунка видно, что атом замещения Te Cd вносит вклад в оба пика (рис. 8, б)

и преимущественно p -электронами, хотя небольшое количество s- и d- электронов присутствует в районе 2А 1 ^а и Е ^а соответственно. Te 1 в подтверждение тому, что было сказано выше, вносит вклад только в формирование 2А 1 ^а уровня. Три эквивалентных атома Te₂, Te₃ и Te₄ главным образом участвуют в формировании уровня в зоне проводимости, но также вносят немалый вклад и в уровень запрещенной зоны. Необходимо также отметить, что основную роль в формировании связей играют p- состояния.

Дефект замещения в условиях деформаций

Для анализа деформаций кристаллической решетки были проведены некоторые предварительные

Табл. 3. Уровни дефектов и ширина зоны

Расстояние, эВ	Деформация, %	Тип деформации
		1D           {	2D          {	3D
2А 1 а – Е a	0	1.13
	1	1.03	1.22	1.13
(в точке Г)	2	0.99	1.23	1.08
	3	0.94	1.38	1.06
E c – E f	0	0.24
	1	0.19	0.35	0.37
(в точке Г)	2	0.15	0.45	0.45
	3	0.12	0.49	0.59

Табл. 4. Внешние давления, необходимые для деформаций решетки CdTe

Деформация, %	Внешнее давление, кбар
	1D	2D	3D
1	1.65	5.59	14.64
2	3.46	11.14	31.08
3	5.29	16.43	48.81

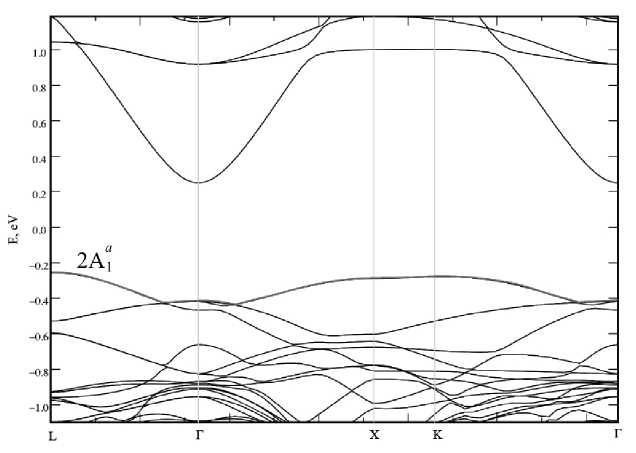
Рис. 10. Зонная структура 128-атомной сверхъячейки CdTe с TeCd при 2 %-м двумерном сжатии. В области Г наблюдается делокализация дефекта изменения в системе координат. Так, вся система координат была повернута таким образом, чтобы ось z была направлена вдоль линии расположения атомов TeCd и Te1 и совпадала с осью симметрии третьего порядка, а оси x и y оказались в плоскости Te2, Te3 и Te4 (рис. 9).

1D -деформация

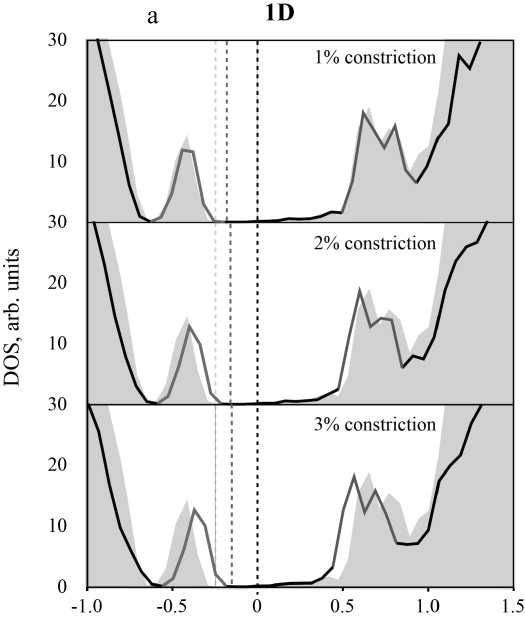
Под одномерной (1D) деформацией подразумевается изменение параметров решетки вдоль оси z (рис. 9), в то время как допускается релаксация атомов в x и y направлениях. Расчеты показывают, что при одномерной деформации уровни дефекта приближаются друг к другу, а уровень Ферми незначительно сдвигается по направлению к зоне проводимости: при 3 %-м сжатии — на 0.12 эВ (Приложение, а; табл. 3). Необходимые для этого давления приведены в табл. 4.

2D -деформация

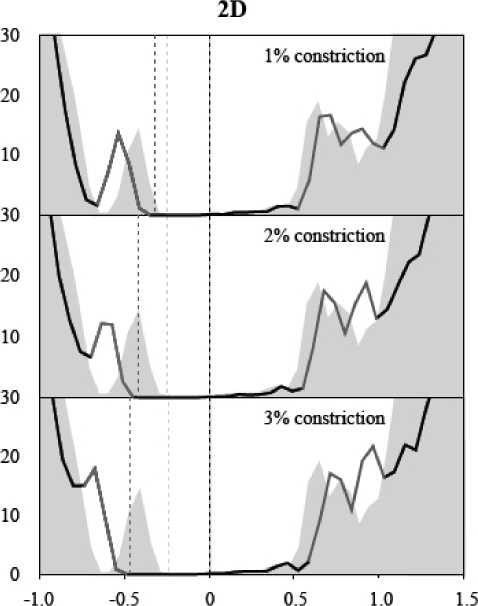
При двумерной (2D) деформации допускалась свободная релаксация атомов только вдоль на- правления z (рис. 9). Параметры решетки в плоскости xy были последовательно уменьшены на 1, 2 и 3 % и зафиксированы. Результаты данной деформации представлены на рисунке (Приложение, b) и в табл. 3. В данном случае уровни дефектов, наоборот (в сравнении с 1D-деформацией), расходятся в разные стороны, увеличивая запрещенную зону на 0.25 эВ при 3 %-м сжатии. Также наблюдается эффект делокализации уровня 2А1а уже при 2 %-м сжатии решетки. На рис. 10 показана зонная структура полупроводника с дефектом при двумерном сжатии решетки на 2%. Из рисунка видно, что уровень дефекта 2А1а сливается с потолком валентной зоны в районе Г-точки.

Необходимые давления при двумерном сжатии также приведены в табл. 4.

3D -деформация

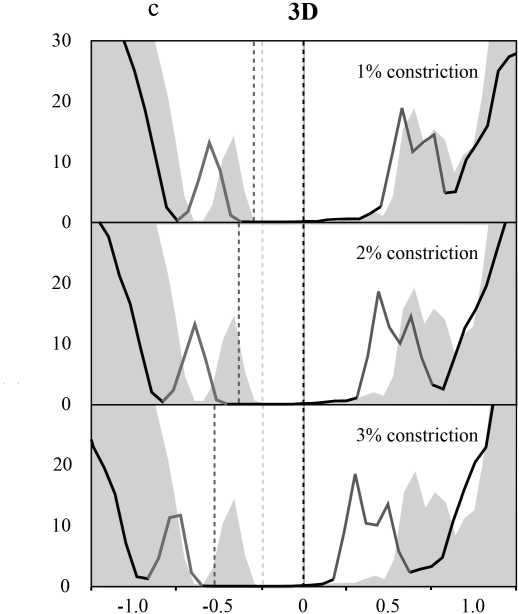
При трехмерной (3D) деформации (гидростатическом сжатии) параметр решетки во всех декартовых направлениях последовательно уменьшался и фиксировался. Так же как при 1D- и 2D-деформациях, сжатие проводилось на 1, 2 и 3 %. Основной тенденцией, отмеченной в данном случае, был сдвиг всех уровней, включая уровень Ферми, в сторону более низких энергий (см. Приложение, с). Также отмечено увеличение запрещенной зоны на 0.35 эВ (табл. 3). Еще одной примечательной особенностью данного типа деформации является сокращение длины "хвоста", с которого начинается зона проводимости за счет сдвига Е ^а уровня.

Давления для трехмерной деформации указаны в табл. 4.

Расчет энергий дефектообразования

В первую очередь энергии дефектообразования рассчитывались для дефекта замещения Te Cd в не-деформированной решетке. Более подробную информацию о способах расчета энергии дефектооб-разования для систем в различных условиях можно найти в работах [4, 9, 10].

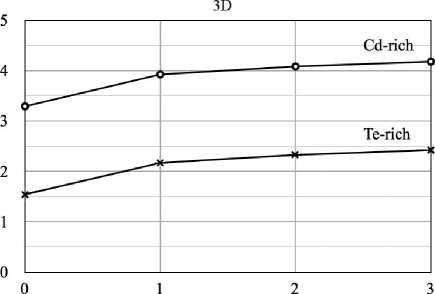
На рис. 11 показаны рассчитанные нами энергии дефектообразования Te Cd для случаев Te-и Cd-насыщенных газовых фаз.

Для теллур-насыщенных условий в качестве химического потенциала теллура µ _Te , используется энергия его кристаллического состояния. Это значение совпадает с максимальным значением химического потенциала теллура в газовой фазе, выше значения которого вместо соединения CdTe начинает формироваться кристаллический теллур.

Для расчета данной энергии была использована тригональная ячейка с тремя атомами теллура. Параметры решетки был вычислены как а = = 4.287 Å (экспериментальное значение 4.457 Å) и с = 5.922 Å (экспериментальное значение — 5.929 Å). Химический потенциал был вычислен как ue - ^ . = -3.805 эВ/атом. (3)

а

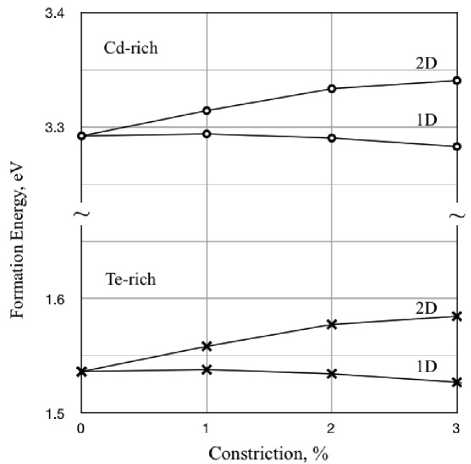
Рис. 11. Энергии дефектообразования Te Cd при одномерном и двумерном сжатии (а), а также при гидростатической деформации (3D) (б)

б

Constriction, %

Зная µ _Te , несложно вычислить химический потенциал кадмия:

µ Cd = µ C^sod^lT^ide - µ T^soe^lid ,                         (4)

где µ _C ^so _d ^l _T ^id _e — полная энергия теллурида кадмия, рассчитанное значение которой составляет –6.035 эВ/(эл. яч.). Используя (2), мы получили энергию формирования дефекта замещения в условиях Te-насыщения Δ H f = 1.491 эВ.

Были проведены аналогичные расчеты для Cd-насыщенных условий.

Решетка Браве кадмия — гексагональная с одним атомом кадмия на элементарную ячейку. Постоянные решетки были вычислены как а = = 3.056 Å (экспериментальное значение 2.979 Å) и с = 6.221 Å (экспериментальное значение 5.618 Å). Химический потенциал кристаллического кадмия

µ _Cd ≡ µ _C ^so _d ^lid = -1.352 эВ/атом.       (5)

64 атомов. Параметр сходимости для сил Фейн-ман—Хельмана в нашей работе 0.01 эВ/Å, а в работе [11] — 0.02 эВ/Å.

ЗАКЛЮЧЕНИЕ

В работе представлены результаты расчетов энергетического уровня дефекта, проведенных для случая нейтрального зарядового состояния Te⁰ Cd .

Определена его геометрия, а также установлены закономерности влияния трех типов деформаций на положение энергетических уровней в запрещенной зоне полупроводника.

Показано, что наиболее эффективной деформацией является одновременная деформация в двух направлениях, которая приводит к уширению запрещенной зоны и расхождению уровней нейтрального дефекта Te Cd , что, несомненно, явится благоприятным фактором для спектроскопических характеристик детекторов на основе теллурида кадмия.

Таким образом, в кадмий-насыщенных условиях энергия, необходимая для формирования дефекта, составляет величину ∆ H_f =3.247 эВ.

Значения, полученные в данной работе, находятся в хорошем согласии с результатами, полученными ранее в работе [11]. Для расчета энергий дефектообразования при деформациях были использованы полные энергии сверхъячеек с дефектом и без него, а также энергия кристаллического CdTe в деформированном соответствующим образом состоянии. Результаты расчетов также приведены на рис. 11.

При одномерной и двумерной деформациях изменения в дефектообразовании незначительны (рис. 11, a). При одномерном сжатии на 3 % энергия дефектообразования Te Cd увеличивается всего на 0.01 эВ, при двумерном сжатии — уменьшается на 0.04 эВ. При трехмерных деформациях картина немного другая. При 3 %-м гидростатическом сжатии (рис. 11, б) энергия дефектообразования Te Cd возрастает примерно на 1 эВ по сравнению с недеформированной решеткой.

Было проведено сравнение с результатами, полученными ранее в работе [11]. Так, при 2 %-м гидростатическом сжатии кристаллической решетки теллурида кадмия энергия дефектообразо-вания Te Cd , полученная в работе [11], возрастает примерно на 0.3 эВ, в то время как в наших расчетах возрастание составляет величину 0.8 эВ. Это может быть обусловлено различиями в построении модели или принятых параметрах сходимости. Так, например, размер сверхъячейки в нашей работе составляет 128 атомов, а в работе [11] —

ПРИЛОЖЕНИЕ

Плотности состояний при одномерной (1D, a), двумерной (2D, b) и трехмерной (3D, c) деформациях (сжатия на 1, 2 и 3 %) кристаллической решетки теллурида кадмия с дефектом замещения

E-Ec, eV

b

DOS, arb. units                                                              DOS, arb. units

E-Ec, eV

E-Ec, eV