Деформация склеры при интравитреальных инъекциях

Исследование известных способов введения лекарственных веществ для доставки их к тканям глаза показало, что наибольшая концентрация создается при интравитреальной инъекции. Так, в стекловидном теле остается до 51,4 % введенной дозы лечебного препарата, а в сетчатке и сосудистой оболочке – до 13,2 %. При других способах введения лечебных препаратов в стекловидное тело, сетчатку и сосудистую оболочку проникает не более 5,3 % введенной дозы [5]. Техника интравитреальной инъекции является относительно простой, а внедрение новых препаратов привело в первом десятилетии XXI века к ее широкому применению (от 325 тыс. интравитреальных инъекций в 2006 году до 1 млн в год в настоящее время, рис. 1) [9, 10, 13].

Бауэр Светлана Михайловна, д.ф.-м.н., профессор кафедры теоретической и прикладной механики, Санкт-Петербург

Количество инъекций, млн

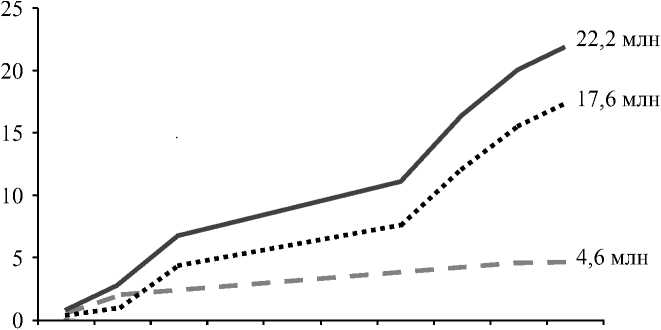
США

Вне США

Всего

Рис. 1. Статистика применения интравитреальных инъекций по данным Market Scope Estimates . Модифицировано с Market Scope ® http://market-scope.com (дата обращения 13.10.2016)

Наиболее опасным осложнением при интравитреальной инъекции является потеря зрения в результате сосудистых нарушений на фоне повышения внутриглазного давления [5]. Введение дополнительного объема жидкости неизбежно приводит к повышению внутриглазного давления в 2,4–38,3 % случаев [11]. При интравитреальной инъекции используются небольшие (до 0,2 мл) дозы лечебного препарата, что приводит к кратковременному увеличению внутриглазного давления, которое считается безопасным для зрительных функций и нормализуется в течение часа [5]. В диссертации [9] изучалось изменение уровня внутриглазного давления после интравитреальной инъекции объемом 0,05 мл. Внутриглазное давление измерялось точечным контактным тонометром ICare Pro ( ICare , Finland ), до введения препарата оно составляло 12–16 мм рт. ст. Измерения внутриглазного давления, проведенные через одну минуту после инъекции, показали, что примерно у половины пациентов уровень внутриглазного давления превысил 38 мм рт. ст., а у ряда больных наблюдалось его повышение до 45–50 мм рт. ст. Однако даже кратковременное увеличение внутриглазного давления выше определенного индивидуального уровня может привести к нарушению кровообращения на сетчатке и в диске зрительного нерва [7], поэтому важно в каждом конкретном случае оценить возможный уровень изменения внутриглазного давления в результате инъекции. С точки зрения механики, это задача определения изменения внутреннего давления в оболочке, заполненной несжимаемой жидкостью, при введении дополнительного объема несжимаемой жидкости.

В работах [3, 4, 12] для оценки изменения внутриглазного давления после инъекций рассмотрена задача трехмерной теории упругости о деформации трансверсально-изотропного сферического слоя, находящегося под действием внутреннего давления. Получена зависимость, характеризующая изменение внутреннего давления в оболочке глаза в зависимости от введенного объема несжимаемой жидкости, а также установлено изменение толщины слоя склеры под действием давления.

Авторы [7] отмечают, что механические свойства оболочек глаза с нормальным зрением и глаз с ошибками рефракции (близорукостью или дальнозоркостью) могут отличаться. Так, для глаз с миопией (близорукостью) модуль упругости в меридиональном направлении может быть меньше, чем модуль упругости в направлении параллели ([7]), корнеосклеральная оболочка в этом случае становится ортотропной.

В работе [6] сделана попытка оценки изменения внутриглазного давления после инъекций, глазное яблоко моделировалось ортотропной оболочкой, но при этом полагалось, что оболочка остается сферической, и рассматривается одно уравнение равновесия. Очевидно, что ортотропный сферический слой при деформации под действием нормального давления перестает быть сферическим, и изменение его напряженно-деформированного состояния не может быть описано одним уравнением.

В данной работе в рамках трехмерной теории упругости рассматривается модель ортотропного сферического слоя, описывающего основную внешнюю, склеральную, оболочку глаза. В рамках этой модели исследуются изменение формы глазного яблока (соотношения длины передне-задней оси глаза и диаметра экваториальной зоны) при повышении внутриглазного давления, а также изменения напряженно-деформированного состояния внешней оболочки глаза при внутриглазных инъекциях.

Постановка задачи

Рассматривается ортотропный сферический слой с внутренним радиусом R ₁ и внешним R ₂ , толщиной h = R ₂ - R ₁ . Положение точки сферического слоя описывается сферическими координатами: ρ – радиальная координата, ϕ – координата в меридиональном направлении, θ – координата в окружном направлении (рис. 2). Будем рассматривать осесимметричную задачу при отсутствии внешних сил, т.е. полагать, что перемещения не зависят от угла θ , а касательные напряжения σ_ρθ , σ_ϕθ и деформации ε_ρθ , ε_ϕθ равны 0. Таким образом, система уравнений равновесия примет вид [1]

∂σρρ +1∂σρϕ ∂ρ ρ ∂ϕ

cotϕ

+ρ σρϕ

+ρ1(2σρρ-σϕϕ-σθθ)=0,

∂σρϕ+1∂σϕϕ+3σ

∂ρ ρ ∂ϕ ρ 1

cotϕ

+ρ (σϕϕ

-σθθ )=0.

Для осесимметричной задачи перемещения точки сферического слоя задаются проекциями вектора перемещений ( w , u ) на направления ρ , ϕ соответственно.

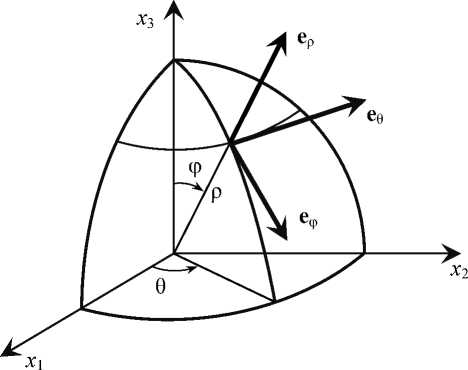
Рис. 2. Ортотропный сферический слой

Деформации и перемещения сферического слоя связаны соотношениями [8]

д w        1 д и  w            и  w        1 f 1 д w  и   д и '

8рр — ^, -        + “  8ее — COt ф- + -, £рф=-  + — др        р дф  р            Р  Р        2 V р дф  р  др J

Уравнения состояния, связывающие напряжения и деформации, для ортотропного тела содержат девять независимых упругих постоянных: Eр, Eф, Eе - модули Юнга, уфр, уер, уеф - коэффициенты Пуассона, _рф, _фе, _ре - модули сдвига:

^£ рр

= E р "'

у фф ф

^v ре ° ее ,

E е

8 —^

^ре    G рe ’

⁸ ее

⁸ фф

V фр в	-а	1 + —	о	у фе в	' °ее ,	F = Я т1
E р	рр	E ф	фф	E е		8 фе п _ фе
_ уер в		у еф в	^,,	1 + —	° ее ,	с — °рф 8               .
E р	рр	E ф	фф	E е		рф _ рф

.

,

В силу симметрии соотношений (3) имеют место равенства

E ф У _ф р ^{— Е} р У рф ,   E ф У фе ^— E е У еф ,

E е% ^— E р V рe .

Введем следующие обозначения

E р —

v* „уфе^уФрур!

^у фе ₃                 ,

^{1   у} ер ^у р„

у* — уер+уефуфр ер фр рф

E р

*

¹ -V р ₆v₆ р

*

V V рф фр

,

*

V фр

*

у рф

*

ф

^у фр ^+у фе ^у ер

^{1   у} ер ^у р„

^у рф ^+у еф ^у ре

¹ -^у фе ^у еф

E ф

*

¹ -V ф ₆v₆ ф

,

,

*

^у еф ^—

V e

*

v v фр рф

^у еф ^+у ер ^у рф

1-У У , фр рф

^у ре ^+у фе ^у рф

^{1   у} фе ^у еф ^,

*

E е ^—

E е

1       *

¹ -V еф V фе

*          , уеруре

причем

Е у ^ф

*

*

фр

^— Е у

рф ’

* *           * *

E ф ^у фе ^— E е ^У еф ,

*

*

E е ^у ер

* *

^— E р ^у ре .

Тогда уравнения равновесия в перемещениях запишутся в виде [2]

где

д ² w

д w

д ² w

д w

д ² и

---z~ + C i + С 2 г^- + С з + С 4 w + С 5------ др ²     др дф дф         дрдф

д ² и , д и , д ² и , д и ,      ,

—— + d, --+ d ₇ —— + d,-- + а.и + d.

’         1                2       2         3                4

дф дф

др

др

, д² w ⁵ дрдф

д и    д и

+ с, --+ с₇-- + с_йи — 0,

6               7               8           7

др дф

, д w   , д w , _A

+ de --+ d₇-- + d₈w — 0,

6                7                8

др дф

дф

^С1 ^— * ^р

с - 2

рф

2 р ² E р ’

с ₃ — с ₂ cot ф , с ₄

р ²

*

у рф

* ре

E ф (1 + 2 у фе ) + E ₈ *

E

- *

,

р

^С 5

р

*

V рф

__рф

2 E.

c 6

_ cot ф

р

* ^у ре

V

G ^

+ _ф

*

² E р 7

c 7

р ²

* урф

в

E *

-7 (1 + У *_ф6

77 * \ фе

^Е р

в

^

G w

*

2 E

,

р 7

^С 8

cot ф р ²

*

V

V

в

E ф ^у фе

E

+ E е

*

в

рф

*

р

2 E

,

р 7

а также

,   2 я 1 Еф    я я ♦ я 2 li  E.V     E , d 1 = —, d2 = ———, d3 = d2cot ф, d4 =—2 1 +     +—— cot ф

^{P        P G} pф                        ^р l     ^G pф    ^G pф

**                   *

= 1 1 + 2 E ^ , d = 250УФ _E L(v * pl      ^G p. )    6 P ^g p.^V "

-^V P9

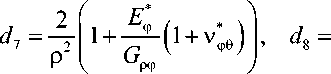
2 cot ф E - ^- E *

P ^{2      G} p-

Рассматривается только область сферического слоя, для которой 0 < ф < — и

R₁ < р <  R ₂.

На части границы ф = 0, ф = 2 полагаем fn)     5w       5 w Г п)

u (P,0 ) = u IP,- 1 = 0, —(P,0) = —IP,- 1 = 0.

l 2 J      5ф        дф l 2 J

На части границы p = R₁ и p = R ₂ считаем заданными значения внутреннего P₁ и внешнего P ₂ давлений.

°pp( R1, ф) = - P1, °pp( R2 , ф) = - P2, °рф( R1, ф) = °Рф(R 2, ф) = °.

Напряжения связаны с перемещениями соотношениями fdw vpф+vp6    урф 5u vp6 cot ф

° PP

+—w +       + l5P     р        р 5ф P

_ Gрф f 1 5w  u5 рф 2 Ip 5ф  p  5Pj

Уравнения (7) и граничные условия (10)–(11) образуют краевую задачу.

В силу положительной определенности упругого потенциала его коэффициенты должны удовлетворять критерию Сильвестра, из которого вытекают неравенства [8]

^у рф <

E L _v< f E Z _v< J E Z E р ’     ^pe ^ E р , ^ф6 E^E ф ,

. 111 V рф V фe V 9р < 2 ^{1 -} _V|

. 2 E p ^рф E ф

. 2 Е ф ^ф6 E ₈

_v ² E e e ^p e

Результаты

Для нахождения численного решения в программном пакете Maple^TM ( v. 18) реализован метод сеток с использованием стандартных представлений производных в конечно-разностной форме.

В конечно-элементном пакете COMSOL Multiphysics ( v. 5.0) построена двумерная осесимметричная модель ортотропного сферического слоя. Добавлено дополнительное уравнение, связывающее давление на внутреннюю поверхность слоя с внутренним объемом глаза.

Расчеты проводились для сферического слоя из ортотропного материала, близкого к трансверсально-изотропному, т.е. полагались выполненными равенства

EP= E1, EФ = E, E9= E (1 + ц), V6v=V, V9p=vep=v1, G„= G + 9 G '=      + 9 G'. C„ = G„ Gp9 = G +9 G".

2 (1 + v)

где ц <<  1. При 9 = 0 материал становится трансверсально-изотропным.

В качестве примера рассматривался ортотропный слой со следующими значениями параметров: E _ф = E = 5 МПа, E _p= E 1 = 0,05 МПа, v = 0,49, v , = 0,01, R ₂ = 12,25 мм, R ₁ = 11,65 мм [2].

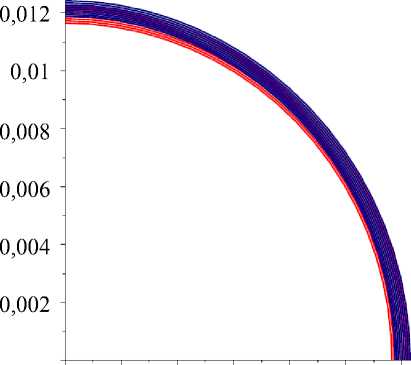
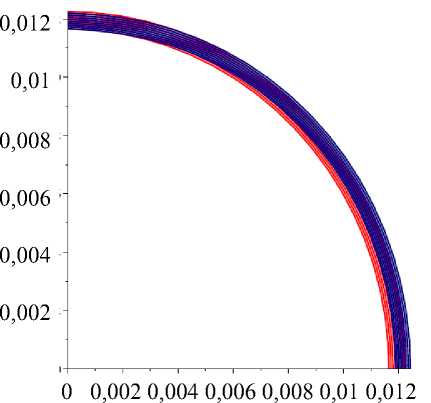
На рис. 3 представлены профили ортотропного слоя до и после деформации, а также распределения перемещений в слое при P ₁ = 60∙133,3 Па ( P ₁ = 60 мм рт. ст.) для

0,012

0,01

0,008

0,006

0,004

0,002

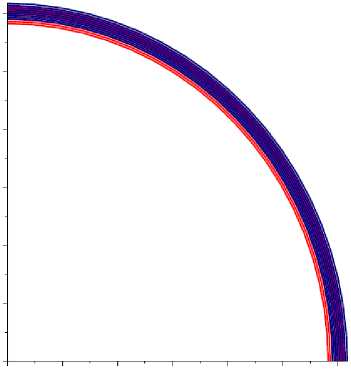
0 0,002 0,004 0,006 0,008 0,01 0,012 а

0 0,002 0,004 0,006 0,008 0,01 0,012

б

в

Рис. 3. Ортотропный сферический слой до и после деформации при P 1 = 60 мм рт. ст.: a - при E ₉/ E _ф = 1 ( ц = 0); б - при E ₉/ E _ф = 1,3 ( ц = 0,3);

в - при E ₉/ E _ф = 0,7 ( ц = - 0,3)

трех значений E ₉/ E _ф при ц = 0, ц = 0,3, ц = - 0,3. Красным цветом обозначен недеформированный слой, синим – слой после деформации.

Численное моделирование показало, что в случае увеличения внутреннего давления, в отличие от трансверсально-изотропного сферического слоя, остающегося сферическим при деформации, ортотропный сферический слой принимает эллипсоидальную форму. Так, для ц >  0 глаз принимает форму вытянутого эллипсоида, а при ц <  0 - форму сплюснутого эллипсоида. В случае внутриглазного давления 15 мм рт. ст. и ц = 0,3 передне-задняя ось глаза увеличивается на 0,038 мм, при ц = - 0,3 - уменьшается на 0,075 мм. При этом внутренний объем глаза увеличивается, если ц = - 0,3, и уменьшается при ц = 0,3.

При моделировании интравитреальной инъекции слой сначала нагружался начальным внутренним давлением, а затем определялось давление, необходимое для изменения внутреннего объема на величину, равную объему вводимого препарата. В пакете Maple^TM ( v. 18) объем деформированного слоя вычислялся как объем эллипсоида вращения. За длины полуосей принимались длины горизонтального и вертикального диаметров слоя после деформации. В COMSOL Multiphysics ( v. 5.0) внутренний объем вычислялся как объем тела вращения. Площадь плоской фигуры, ограниченной деформированной внутренней гранью слоя, рассчитывалась с помощью формулы Гаусса–Остроградского. В табл. 1 приведено относительное изменение внутреннего объема слоя в зависимости от параметра материала µ. Можно заметить, что уменьшение модуля упругости в окружном направлении ( ц = - 0,3, E ₉/ E _ф = 0,7) приводит к большему изменению начального объема, ограниченного склерой, в сравнении с трансверсально-изотропным материалом ( E₉]E _ф = 1 ) и материалом с модулем упругости, меньшим в меридиональном направлении ( ц = 0,3, E ₉/ E _ф = 1,3).

В табл. 2 представлены значения внутриглазного давления в результате интравитреальной инъекции при введении от 0,05 до 0,2 мл лечебного препарата для ц = 0, ц = 0,3, ц = - 0,3, до введения препарата полагается P 1 = 15 мм рт. ст.

Сравнивая расчеты, приведенные в табл. 2 и 3 при различных значениях µ, можно заметить, что меньшему значению внутреннего объема склеры до инъекции ( ц = 0,3) может соответствовать большее увеличение внутреннего давления после введения дополнительного объема жидкости.

Влияние свойств материала слоя на уровень внутриглазного давления после интравитреальной инъекции показано на рис. 4. При расчетах предполагалось, что до нагружения физиологическим давлением в 15 мм рт. ст. внутренний и внешний радиусы слоя равны R ₁ = 11,5 мм, R ₂ = 12,1 мм. Значение модуля упругости в направлении толщины принималось равным E _р = E _ф /100, а значения коэффициентов

Таблица 1

Относительное изменение внутреннего объема слоя

Значение внутриглазного давления, мм рт. ст.	Относительное изменение внутреннего объема слоя после деформации, Vdef V 0
	ц = 0		ц = 0,3		ц = - 0,3
	Maple	COMSOL	Maple	COMSOL	Maple	COMSOL
15	1,0104	1,009	1,0101	1,008	1,011	1,012
60	1,042	1,04	1,041	1,03	1,044	1,05

Таблица 2

Объем инъекции, мл	Давление в корнеосклеральной оболочке глаза после инъекции, мм рт. ст.
	µ= 0		µ = 0,3		µ=- 0,3
	Maple	COMSOL	Maple	Maple	COMSOL	Maple
0,05	25,7	27,5	26,1	29,7	25,3	24,7
0,1	36,5	39,9	38,5	44,4	35,6	34,4
0,2	58	64,5	59,4	73,58	56,0	53,7

Таблица 3

Влияние начального объема на уровень внутриглазного давления после интравитреальной инъекции

Объем инъекции, мл	Давление в корнеосклеральной оболочке глаза после инъекции, мм рт. ст.
	R 2 = 10,15 мм, R 1 = 10,75 мм, µ=- 0,3, V 15 = 4427 мм3	R 2 = 11,65 мм, R 1 = 12,25 мм, µ= 0, V 15 = 6683 мм3	R 2 =13,15 мм, R 1 = 13,75 мм, µ= 0,3, V 15 = 9601 мм3
0,05	15,9	12,5	9,7
0,1	31,6	24,9	19,4
0,2	62,9	49,5	38,7

Пуассона полагались такими: ν = 0,49, ν ₁ = 0,01. Видно, что уровень офтальмотонуса после введения инъекции варьируется от 20 до 50 мм рт. ст., что согласуется с данными из [9].

Как было показано в [14], начальный объем оказывает существенное влияние на подъем внутриглазного давления после инъекции. В [3, 7] отмечается, что объемы глаз с различными нарушениями зрения могут существенно отличаться. В табл. 3 для слоев различного начального объема, но одинаковой толщины, приведены значения внутреннего объема после приложения давления в 15 мм рт. ст. ( V 15 ) и значения внутреннего давления после интравитреальной инъекции. Как и ранее, предполагалось, E _ϕ = E = 5 МПа, E _ρ = E ₁ = 0,05 МПа, ν = 0,49, ν ₁ = 0,01.

Выводы

Представлена математическая модель, описывающая напряженно-деформированное состояние внешней оболочки глаза под действием внутреннего давления и после введения дополнительного объема во внутреннюю полость. Показано, что, если модули упругости в меридиональном и окружном направлениях различаются, то сферический слой принимает форму, близкую к эллипсоидальной, под действием нормальной нагрузки.

Выполненные расчеты показали качественное совпадение результатов с клиническими данными [9]. Сведения о геометрии глаза до введения лекарственного препарата позволяют не только предсказать изменения внутриглазного давления после инъекций, но и оценить соотношение модулей упругости в меридиональном направлении и направлении параллели.

Благодарности

Работа выполнена при поддержке грантов РФФИ № 15-01-06311-а, № 16-01-00580-а и с использованием оборудования ресурсного центра Научного парка Санкт-Петербургского государственного университета «Обсерватория экологической безопасности».