Декомпозиция задач управляемости и наблюдаемости двухтемповых систем
Автор: Семенова М.М.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 6 т.23, 2021 года.
Бесплатный доступ
В статье излагается метод декомпозиции нелинейных двухтемповых систем, основанный на теории интегральных многообразий быстрых и медленных движений. Исследуется управляемость, наблюдаемость, стабилизируемость системы. Приведен пример, иллюстрирующий полученные результаты.
Декомпозиция двухтемповых систем, интегральное многообразие, управляемость, наблюдаемость, устойчивость, стабилизируемость, асимптотические разложения
Короткий адрес: https://sciup.org/148323289
IDR: 148323289 | УДК: 517.9:62-50 | DOI: 10.37313/1990-5378-2021-23-6-116-118
Текст научной статьи Декомпозиция задач управляемости и наблюдаемости двухтемповых систем
РАСЩЕПЛЯЮЩЕЕ ПРЕОБРАЗОВАНИЕ
Исследование нелинейных сингулярно возмущенных систем дифференциальных уравнений приводит к решению широкого класса прикладных задач. Использование быстрых и медленных интегральных многообразий позволяет построить преобразование, осуществляющее декомпозицию системы на независимую медленную подсистему и быструю подсистему, описывающую затухающие колебания, что дает понижение размерности моделей и избавляет от вычислительной жесткости. С помощью невырожденного преобразования система сводится к эквивалентной сингулярно возмущенной системе с разделенными переменными, – к системе блочно-диагонального вида, в случае линейных систем, – к системе блочно-треугольного вида, если исходная система нелинейная. С задачами управляемости и наблюдаемости тесно связаны задачи идентифицируемости и стабилизи-руемости. Данная работа посвящена изучению свойств управляемости, наблюдаемости, стаби-лизируемости двухтемповой нелинейной неавтономной системы.
Цель работы:
. Понижение размерности задачи управляемости, наблюдаемости и стабилизируемости нелинейной двухтемповой неавтономной системы так, чтобы модель меньшей размерности с большой степенью точности отражала все свойства исходной системы.
. Получение достаточных условий, управляемости, наблюдаемости и стабилизируемости сингулярно возмущенных систем.
Рассмотрим модель сингулярно возмущенной системы вида ex — a(t,x,i,s) = b(t,x,£)u,w = ф(1,х,х,в), (1) где хЕХ с Г,и El/сГ – управляющие воздействия, wEV a – измеряемая координата, а.фЕ R”, – матричная функция размерности Функции a, b, ф равномерно непрерывные и ограниченные вместе с достаточным числом частных производных по всем аргументам, t E H Обозначим y = x. Модель (1) примет вид x = y,sy = a(t,x,y,c) + b^t.x.E^u.w = Ф(1,Х,У,е\ (2)
Пусть система (2) удовлетворяет следующим условиям [1]:
Уравнение a(t, x, y, 0) = 0 имеет изолированное решение у = ^(t,x).
В области П = {(t,X,y,E): lly — fc0(t,x)|| < p,E E (0,Efl]} функции a, h0 имеют достаточное число равномерно непрерывных и ограниченных частных производных по всем переменным.
Собственные значения Xt = Aj(t,x),i = l,n матрицы ^ (t,x, hQ(_t, x),0) удовлетворяют неравенству Re Xt<-p < 0.
В системе (2) произведем замену переменной x(t) = v(t) + sH(t, v(t),z(t), E),H(t, V, 0, e) = 0,y(t) = z(t) + /l(t,x(t),£). В ре -зультате получим систему блочно-треугольного вида v = h(t,v, e) + b(t, v,eH, e^u, ez = Z(t,v,z,s) + b(t, v, eH, e^u, w = фг (t, V, z, e), (3)
где 7 7 7.7 7 = - —- 7 7 : 7_z' 7 ■ Г 7
v, еН ,z, е) = a(t, v + еН, z+K,e)- a(t, v +еН, h, s) — s |^ (t, v + eH, s)z, ф±{£, v, z, Функции
7 7 77 E Л 7 '7 Z 5 • МОЖНО искать В виде асимптотического разложения [2] 7 7 /7 _- ■ = ^^.^ - е" z:. 7 77 ■ из уравнения £ + £ ^ Mt, х, е) = a(t, х, Mt, х, е), е), и л 7 / : 7 ■ = L-:i ■ _-" .4.. 7 / z ■ из уравнения ан ан, , . ан , . _
Е --Ь £--п( t, Е ) 4-- Z ( V, Z, Е ) = at dv v v dz х '
z + h^t, v + еН, е) — Mt> v, е)
УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ
Для исследования свойств управляемости и наблюдаемости блочно-треугольной системы (3), Мф, 0,0,е) = O,Z(t, 0,0, е) = 0, линеаризуем ее по переменным состояния вдоль v = 0, z = 0: v = ^ (t, О, s)v +
b(t, 0,0, s)u + Mt, 0, s) + at(t, v,z,u, e), ez = ^ (t, 0,0, s)v + ^ (t, 0,0, s)z + b(t, 0,0, e^u + Z (t, 0,0, s) + a2 (t, v, z, u, s), w = ^ (t, 0,0, e) v + ^ (t, 0,0, e^z + a3 (t, v, z, e).
Обозначим,
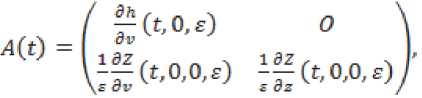
наблюдаемости динамических систем по линейному приближению [3], получаем условия управляемости и наблюдаемости системы (3). Так как система (1) получена из системы (3) с помощью невырожденной замены переменных, то исходная система (1) вполне управляема и вполне наблюдаема.
Пример. Рассмотрим модель системы математических маятников с трением [4], подвешенных к несущему телу ? перемещающемуся горизонтально с ускорением ./:
Еф, + 2yt t
= a^,to^= j^,i = T?n;p = Е”=1с;^р где .' - длина :' маятника, _- :- 2 - малый положительный параметр, '.' > 2 „ - частота малых колебаний 7. маятника, z /7 - коэффициенты, отличные от нуля, :. < 1. Обозначим, ■_ = _■ тогда система примет вид:
ф, = ф^Еф^ = (”О)2 COSCOjt — SO)?) Sin ф, —
- ^Yt^i + “i^.i = Vn;p ='Ei=lci Произведем замену переменных следующего вида: , , a;tu? coB *'=z'+ ■ siny, + £(а;О>? sino,^ — ^^t ^“t1-^ ™S ^ = )t^ + °(£2X c(0 = (^(0 c2(t)), c^t) = (t, o,o £),C2(t) = ^^ (t, 0,0, E),p(t,U, s) = / ^-(ii(t, 0,0, e)iz) y-(b(t,0,0,E)u) \-^-(b(t, 0,0,e)u) (bit, 0,0, s)ti) \E 3v v v E dzv xJ (а;ш? совы,Г-у)2 f2> —----(1 — cos 2v,) )и + О ( е ) : le^i^i vv ■ - g-a^\coBGitt\ £Zi = (-2^ +e------cosv^z, + a(U + O(f2);p = £?=1С; (v, - s^ + O(e2) Запишем линеаризованную систему в матричном виде: + o(||(v z)'||)p1(t,u,s),w = = C^(z) +аз(^^^£)' Используя теоремы об управляемости и Используя теоремы об управляемости и наблюдаемости динамических систем по линейному приближению, получим, что система блоч- но-треугольного вида вполне управляемая и вполне наблюдаемая, так как система нулевого приближения вполне управляема, а система первого приближения вполне наблюдаема. Так как система блочно-треугольного вида получена из данной с помощью обратимой замены пере- менных, то данная система является вполне управляемой и вполне наблюдаемой.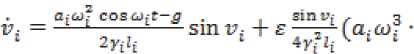
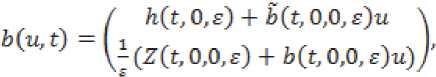
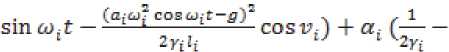
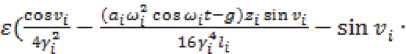
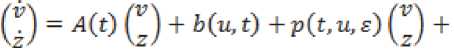
Список литературы Декомпозиция задач управляемости и наблюдаемости двухтемповых систем
- Васильева, А.Б. Асимптотические методы в теории сингулярных возмущений / А.Б. Васильева, В.Ф. Бутузов. - М.: Высшая школа, 1990. - 208 с.
- Воропаева, Н.В. Геометрическая декомпозиция сингулярно возмущенных систем / Н.В. Воропаева, В.А. Соболев. - М.: Физматлит, 2009. - 256 с.
- Габасов, Р. Качественная теория оптимальных процессов / Р. Габасов, Ф.М. Кириллова М.: Наука, 1971. - 508 с.
- Богаевский, В.Н. Алгебраические методы в нелинейной теории возмущений / В.Н. Богаевский, А.Я. Повзнер. - М.: Наука, 1987. - 256 с.
- Chen, C.C. Criterion for global exponential stabilisability of a class of nonlinear control systems via integral manifold approach / C.C. Chen // IEE Proc.-Control Theory Appl. V. 147. № 3. May 2000. P. 330-336.


