Деление отклика ядерной спиновой системы аморфного полимера на упругий, вязкий и вязкоупругий

Известно, что данные по ядерной магнитной релаксации в аморфных полимерах описываются теорией Бломбергена, Парселла и Паунда [1], модифицированной введением спектра времени корреляции (СВК) [2-6]. Форма СВК определяется динамикой движения полимерных молекул. Поэтому для получения детальной информации о характере этого движения необходимо как можно точно определять форму СВК. Первой целью данной работы является нахождение связи между поведением ядерной спиновой системы полимеров выше температуры стеклования в импульсном ЯМР-эксперименте и формой спектра времен корреляции. Аналогом СВК в релаксационной спектрометрии является спектр времен релаксации механического напряжения. В свою очередь, в релаксационной спектрометрии [7] отклик полимерного образца на механическое воздействие в зависимости от температуры и периода или времени действия нагрузки может оказаться либо упругим, либо неупругим (вязким), либо вязкоупругим. В связи с этим вторая цель нашего исследования заключается в том, чтобы показать, что отклик ядерной спиновой системы на импульсное воздействие радиочастотного поля также может быть разделен на упругий, вязкий и вязкоупругий. Такой подход позволит не только терминологически сблизить различные методы исследования, но и рассматривать их результаты с единых позиций.

Теория

Теоретическое рассмотрение начнем с предположения, что спиновая система однородна и описывается одним для всех ядерных спинов временем корреляции т_с, то есть нормированная функция корреляции представляет собой простую экспоненту

^(/) = ехр(-//тс

Предположим далее, что процесс модуляции диполь-дипольного взаимодействия ядер является гауссовым. Тогда нормированный спад поперечной намагниченности (СПН) J2(0 согласно [8] будет иметь вид:

Л2(/) = ехр -<т2Тс

—-1 + е

где о² - второй момент жесткой решетки в частотных единицах. Функция (2) при t < т_с является гауссовой

^2(?)=ехр _

гл a t

а при t > г_с - экспоненциальной

^2(z) = exp

V 7

где 7) = 1/(<т2тс). Вид функции (2) приведен на рис. 1. Переход от гауссовой формы к экспоненци альной, как видно из рис. 1, происходит в момент t = тс(в полулогарифмическом масштабе гаус сова кривая представляет собой параболу, а экспонента - прямую). Гауссова форма СПН характерна для твердого (неупорядоченного) тела [6, 9], а экспоненциальная - для жидкости. Также как и при рассмотрении реакции материала на механическое воздействие отклик спиновой системы при малых временах наблюдения, когда t < тс, будем считать упругим, а при больших, когда t > тс - неупругим или вязким.

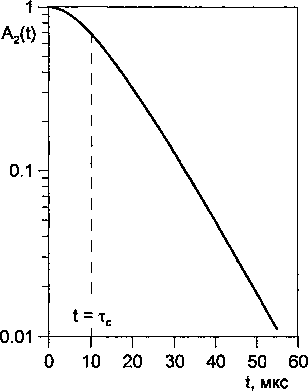
Рис. 1. Спад поперечной намагниченности Дг(0> построенный согласно (2) в полулогарифмическом масштабе. 0^=1010с"2

Теперь выясним, как ведет себя спиновая система при действии твердотельных последовательностей импульсов (ТПИ) 9О°-т-9О°9о и MW-4: 90°₀-т-(90⁰₉о-2т)„, где т - интервал времени между радиочастотными импульсами, п - количество циклов, подстрочный индекс - фаза высокочастотного поля в градусах. В твердых телах такие последовательности импульсов вызывают появление сигналов солид-эхо [10], а в жидкостях нет.

Согласно [11], время 7^/, характеризующее затухание огибающей сигналов в последовательности MW-4, определяется выражением

1       2

----= с тс T2ef

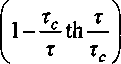
Из (5) следует, что при коротких раздвижках между импульсами, когда т < т„ благодаря возникновению сигналов солид-эхо, время Г_2е/> 7) (Г₂ = (д^сУ) и зависит от т. Напротив, при больших раздвижках между импульсами, когда т > т_с, сигналов солид-эхо не возникает, время Ti_ej = 7₂ и не зависит от т. С учетом выражения (2) делаем заключение, что сигналы солид-эхо возникают только в том случае, когда второй импульс ставится на гауссову часть СПН, и отсутствуют, когда второй импульс достаточно удален от первого, и СПН имеет экспоненциальную форму. В терминах, принятых в релаксационной спектрометрии, возникновение сигналов солид-эхо, равно как и зависимость Т^ от интервала т при т < т_с, соответствует упругому, в то время как отсутствие солид-эхо при т > т_с - неупругому отклику спиновой системы.

Аналогичное разделение отклика спиновой системы на упругий и неупругий можно сделать и для времен спин-решеточной релаксации как в лабораторной Тх, так и во вращающейся системах координат Тх_р. В таблице произведена систематизация откликов спиновой системы в различных импульсных ЯМР-экспериментах. В этой таблице <о₀ и 6o_t - резонансная частота в лабораторной и вращающейся системах координат, соответственно.

Таблица

Деление отклика ядерной спиновой системы на упругий и неупругий при движении, характеризуемом одним временем корреляции тс

Вид или параметр отклика	Характер отклика
	упругий (условие)	неупругий (условие)
Тх, Тхр Tief Т1	?Up ~ ^ОДТс («>0,1Тс >1) Tief- Тс/Т2 (Те >  т) Т1 = const (тс > x)	Т 1Др ~ тс (со^дтс < 1^ Tief ~ ^с (jc < ^ Т1 - if (тс< ох)
форма Ai(t)	гауссова (/ < тс)	экспоненциальная (/ > тс)
наличие сигнала солид-эхо	есть (тс > т)	нет (тс< т)

Перейдем к рассмотрению поведения ядерной спиновой системы при движении, описываемом непрерывным спектром времен корреляции. В литературе имеются данные о поведении времен ядерной магнитной релаксации при введении в рассмотрение спектров времен корреля- ции той или иной формы [2—4]. Однако анализ влияния спектров времен корреляции на спад поперечной намагниченности в литературе отсутствует. Поэтому исследование связи формы СВК с формой спада поперечной намагниченности проведем в данной работе. Параллельно с этим рассмотрим вопрос о влиянии спектра времен корреляции на отклик спиновой системы при действии твердотельных последовательностей.

Как и прежде будем исходить из того, что модуляция ядерного диполь-дипольного взаимодействия является гауссовой и спиновая система однородна. Однако теперь в отличие от (1) функция корреляции является неэкспоненциальной и имеет вид

^(0=/<7(тс)ехр -— UT<

О            \ ^Тс)

где G(t_c) - нормированная функция распределения времен корреляции. С учетом принятых предположений СПН примет вид:

А(0 = ехР

-Jg(tc)<72tc2(--1 + /t^t(

О             Тс

Разобьем шкалу времен корреляции на сколь угодно малые, но равные участки Зт_с и перепишем функцию (7) в виде:

T_d +дт_е                       __ L

A2(t) = exp

-^ J О(г_с)а²т^-1 + е ^T=)dr_c

Положим далее, что функция

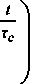
является ступенчатой: изменяется скачком в точках тс„ но в пределах каждого интервала Зтс остается неизменной. Тогда после введения обозначения функция (6) преобразуется к виду

где

Tei*6tc

Pi = f <7(r_c)Jr_c

л (0 * ехр

2 V  2

-° LPiT«

--1 + e ^CT

Перепишем (10) в более удобной для анализа форме

A2i^ = exp -р^т2

——1 + e Tci

(H)

Согласно (11) СПН состоит из произведения различных по форме компонент A 2,(0- Компоненты, для которых ptcPta > 1, имеют гауссову форму, а компоненты с р^Тс? < 1 затухают по экспоненциальному закону. В итоге, результирующая функция A^f) имеет форму, промежуточную между гауссовой и экспоненциальной. С точки зрения релаксационной спектрометрии СПН обладает одновременно как упругими, так и неупругими свойствами, то есть является вязкоупругим.

Гауссовы компоненты-сомножители произведения (11), отражающие твердотельные или упругие свойства спиновой системы, при действии ТПИ образуют сигналы солид-эхо. При этом время затухания огибающей сигналов солид-эхо каждой z-той компоненты превышает время T2i этой же компоненты и зависит от временного интервала между импульсами т (T2eji ~ т2), что соответствует упругому отклику. Напротив, экспоненциальные сомножители спада (11) отража- ют жидкостные или неупругие свойства спин-системы. Поэтому при действии ТПИ возникающий сигнал совпадает с СПН (то есть 7^ = Ту) и время T2i не зависит от т. Результирующая огибающая сигналов солид-эхо, представляющая собой вязкоупругий отклик, будет затухать по закону Ту/~ т”“, где а (в зависимости от формы СВК) заключено в пределах от 0 до 2. Из изложенного выше следует, что сигналы солид-эхо возникают только в том случае, когда второй импульс в ТПИ прикладывается в такой момент времени, когда спад поперечной намагниченности после первого импульса имеет гауссовоподобную форму.

Представим спектр G(t₆) в форме F(S), где

5'=1п(т/тс0), (13)

Тео - наивероятнейшее время корреляции. При этом GQt_c)dT_c = F(S)dS и F(S) = t_cG(t_c). Теперь покажем, как форма СПН связана с формой таких спектров времен корреляции, которые со стороны больших времен корреляции содержат медленнозатухающее крыло. Такими свойствами обладают спектры Фуосса-Кирквуда, Кола-Кола и Гаврильяка-Негами. На таком крыле функция распределения имеет вид

(14) где р, являясь, с одной стороны, параметром ширины спектра, определяет скорость затухания этого крыла. Расчет, проведенный нами для спада поперечной намагниченности согласно (7) при наличии спектров Фуосса-Кирквуда, Кола-Кола и Гаврильяка-Негами в случае, когда т^ст2 « 1, дал

Л2(0*ехр

-<»2 ^ гу-" .

V к )

где а = 1, з!п(/?лу2) и 5sin(STi/2) для спектров Фуосса-Кирквуда, Кола-Кола и Гаврильяка-Негами, соответственно; 3 - второй параметр ширины в спектре Гаврильяка-Негами.

Согласно (15) при увеличении Р от 0 до 1, соответствующем переходу от бесконечно широкого спектра к бесконечно узкому, форма СПН изменяется от гауссовой до экспоненциальной. Если определить время Г₂, как время уменьшения J₂(0 ^в е Р³³ от своего начального значения Л₂(0), то из (15) получим, что

Р

Т₂~^~^                         (16)

Как известно [2], параметр р определяет частотную зависимость параметров Т_х, Т_Хр и Т^, а именно, при выполнении условий оо^со « 1, CDiTco « 1, т_со << т соответственно имеет место

Т_х ~ o)₀^vW, Т_Хр~ cW, T_2ef~^4^.               (17)

Из (15) и (17) следует, что форма СВК, определяемая параметром р, оказывается однозначно связанной как с формой СПН, так и с частотными зависимостями времен релаксации Т_х, Т_Хр и Т^у. Кроме того, из соотношений (15)—(17) следует, что форма спектра определяет зависимость параметров Т_х, Т_Хр, Tiej-и Т₂ от Тсо и, следовательно, от температуры. Очевидно, что если СВК может быть представлен зависимостью (14) с изменяющимся вместе с S значением Р, то соответствующие изменения произойдут как в частотных и температурных зависимостях времен релаксации Т_х, Т_Хр, Т_2е/И Т₂, так и в форме СПН. В практическом плане важно то, что параметр р, определяющий кривизну СПН в момент времени т - момент приложения второго 90°-ного импульса в последовательности MW-4, определяет и наклон зависимости IgT^/lgr) в тот же самый момент т. Легко показать, что при наличии спектров времен корреляции, имеющих быстро затухающие низкочастотные крылья (спектр Кола-Давидсона, прямоугольный и log-гауссовый спектры), когда т^о² « 1, сигналы солид-эхо образовываться не должны, а СПН должен иметь экспоненциальную форму.

Обобщая литературные данные и используя результаты нашего исследования, мы составили перечень характерных особенностей поведения ядерной намагниченности при одновременном выполнении условий т^о2 « 1, сооТео « 1, coiled « 1 в зависимости от формы низкочастотного крыла спектра времен корреляции. При наличии СВК с медленно затухающим низкочастотным крылом вида (14) (спектры Фуосса-Кирквуда, Кола-Кола, Гаврильяка-Негами) отклик является вязкоупругим и имеют место: а) частотная зависимость (дисперсия) времен релаксации Тх, ТХр и T2ef, б) зависимость между временами релаксации Тх, ТХр, T2ef, Т2 и обратным временем корреляции r^f1 не является прямо-пропорциональной, в) гауссовоподобная форма СПН; г) возникнове- ние сигналов солид-эхо при действии ТПИ; д) отсутствие равенства между временами релаксации Ть Tip, Tief, Тг, а именно: Тг < ТХр < Тх или Тг < Т^< Ti. Для спектров же с крутым низкочастотным крылом (спектр Кола-Давидсона, прямоугольный и log-гауссовый спектры) отклик является неупругим и в этом случае: а) отсутствует дисперсия времен релаксации ТХ, ТХр и 72е/и их равенство друг другу; б) наблюдается прямо-пропорциональная зависимость между временами 7*1, Т1Р и Tie/ и Тео”1; в) СПН экспоненциален; г) сигналов солид-эхо не возникает. Для иллюстрации изложенного выше на рис. 2 приведены результаты расчета функции спада поперечной намагниченности Xi(0 и релаксационной функции продольной намагниченности в условиях спин-локинга Л1р(<) для спектров log-прямоугольного и Фуосса-Кирквуда одинаковой ширины на полувысоте при условии, ЧТО T?cOff « 1.

Сравнение с экспериментом

Теперь проанализируем результаты экспериментов, проведенных нами ранее [5, 9, 14], и изучим действие твердотельных последовательностей импульсов в аморфных полимерах: полиизобутилене (ПИБ) с молекулярной массой М ~ 2Т О⁵, натуральном каучуке (НК) с М ~ 10⁶ и цис-1,4-полибутадиене (ПБД) с М ~ 10⁵ в широком температурном диапазоне - от температуры стеклования до температур, при которых полимеры находятся в высокоэластическом состоянии.

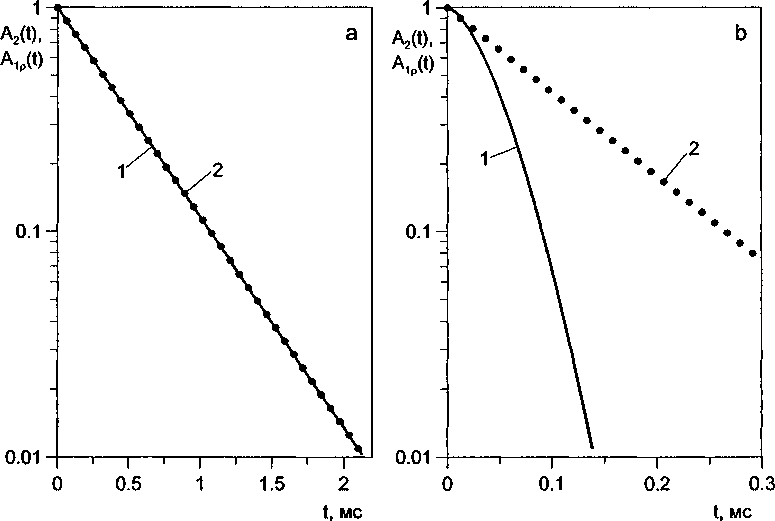
Рис. 2. Спад поперечной намагниченности Д₂(0 (1) и релаксационная функция продольной намагниченности Ai_p(t) (2) в условиях спин-локинга (си, = 2,67-10⁴ рад/с) для двух спектров времен корреляции одинаковой ширины на полувысоте: loq-прямоугольного (рис. 2а) с /дД = 2 и Фуосса-Кирквуда (рис. 2Ь) с р = 0,42, о² = Ю’° с"², Тео = 10^-7с.

Во всех изученных объектах во всем исследуемом интервале температур при действии ТПИ возникают сигналы солид-эхо, наблюдается дисперсия времен релаксации Ту, Т\р и Tief на высокотемпературной ветви минимумов Ti, ТХр и (или) Tief. При низких температурах зависимость времен Тур и Tief от частоты слабая с параметром р в (14), имеющим значения 0,7, 0,8 и 0,8 для ПИБ, НК и ПБД, соответственно. Время Ti такую слабую зависимость от частоты имеет на всем протяжении высокотемпературной ветви минимума. При более высоких температурах в достаточно широком диапазоне частотная зависимость ТХр и Tief становится более сильной, чему отвечает меньшее, чем ранее значение параметра р; 0,5, 0,5 и 0,55 для ПИБ, НК и ПБД, соответственно. Усиление частотных зависимостей времен релаксации Tip и 7ге/в согласии с (17) и (16) коррелирует с ослаблением температурных зависимостей Tip и Т^ и Ti, построенных в аррениусовых координатах. Как и следовало ожидать, вызванное уменьшением параметра Р ослабление температурного наклона времени Ti сопровождается тем, что СПН принимает ярко выраженную гауссовоподобную форму. Значения р, вычисленные из СПН согласно (16) при температурах, когда зависимость Ti(T) ослабевает (после излома на температурной зависимости Ti), равны 0,45, 0,5 и 0,6 для ПИБ, НК и ПБД, соответственно, и практически совпадают со значениями, полученными из дисперсионных зависимостей Т\р и Т-^ и приведенными выше. Имеющие место при высоких температурах факты уменьшения параметра Р, усиления частотных зависимостей времен релаксации Т\р и Т^у, ослабления температурных зависимостей ТХр, Тъ* и 7г и появления ярко выраженной гауссовоподобной формы СПН свидетельствуют об усилении упругой составляющей в вязкоупругом отклике спиновой системы полимерных образцов и об ослаблении степени затухания спектра времен корреляции при увеличении S. Это подтверждают СВК, построенные на основе данных по ЯМР-релаксации в образцах ПИБ и цис-1,4-полиизопрена с Л/ ~ 106 в работах [5, 14], приведенные на рис. 3 и 4. Приведенные СВК очень похожи на спектры времен релаксации механического напряжения HL [12], которые также содержат излом на низкочастотной ветви.

В заключении отметим, что это исследование было основано на предположении, что спиновая система является однородной, хотя данные импульсного ЯМР-эксперимента указывают на элементы неоднородности [9, 13], проявляющиеся, в частности, в появлении медленнозатухающих неэкспоненциальных участков в конце спадов поперечной намагниченности. Однако эта неоднородность не сказывается на временах релаксации Т_х, Т_Хр, Т_2е/И, как показано в [5, 14], в первом приближении при описании начальной формы СПН и определении времени Т₂ ею можно пренебречь.

IgF(S)

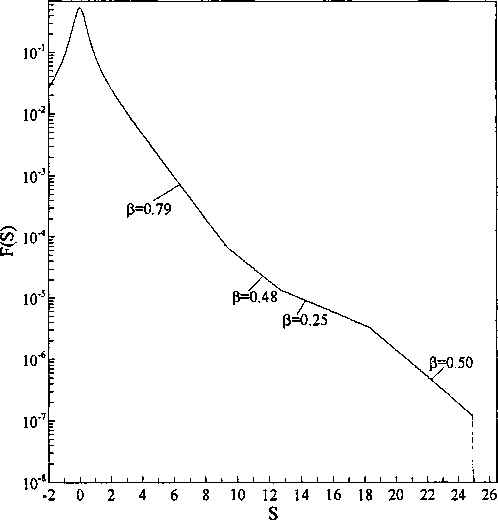
Рис. 4. Спектр времен корреляции, полученный в [14] подгонкой теоретических Т₂, Ti и Г_2ег(т"¹) под экспериментальные для образца цис-1,4-полиизопрена с М *10^е

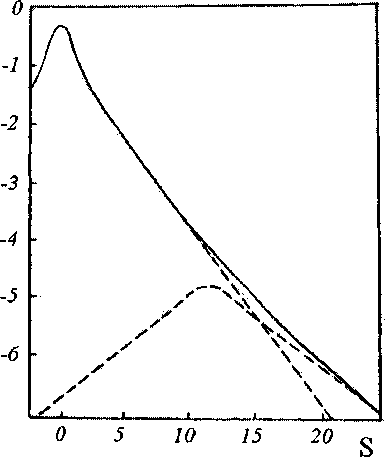
Рис. 3. Спектр времен корреляции, полученный в [5] подгонкой теоретических Т₂, L и Т^Дш) под экспериментальные для образца ПИБ с М я 2-Ю⁵. СВК составлен из двух спектров с параметрами р, равными 0,7 и 0,4, и сдвинутыми друг относительно друга на AS = 11,5

Выводы

• 1.    Показано, что отклик спиновой системы полимерного образца может быть разделен на упругий, неупругий и вязкоупругий в зависимости от времени наблюдения и расстояния между радиочастотными импульсами в последовательности MW-4 и сопоставлен с определенной степенью затухания спектра времен корреляции молекулярных движений.

• 2.    Проведем анализ результатов импульсных ЯМР-экспериментов, выполненных в гибкоцепных полимерах высокой молекулярной массы выше температуры стеклования с точки зрения вязкоупругого поведения отклика спиновой системы. Установлено, что дисперсионные и температурные зависимости времен релаксации Т_Хр, Т_2е/, форма и время спада поперечной намагниченности проявляют упругое и вязкоупругое поведения. При высоких температурах, когда полимерные образцы переходят в высокоэластическое состояние, в отклике спиновой системы усиливается упругая составляющая. Этому переходу в спектре времен корреляции соответствует переход к медленному затуханию.

Автор признателен проф. В.Д. Федотову и проф. А.И. Маклакову за ценные замечания и полезную дискуссию.