Демпфирующая роль желудочков головного мозга при ударе

Закрытое повреждение головы в большинстве случаев является результатом ударных взаимодействий с другим телом. Однако повреждение головного мозга может иметь место и без повреждения (разрушения) непосредственно черепа головы.

В литературе приведены результаты “неударных” экспериментов, в которых голова испытуемого животного ускоряется так, как это было бы при ударном взаимодействии [1, 2], а также при имитации ускоренного движения туловища без каких-либо ударных взаимодействий.

В момент ударного воздействия направление силы удара может не проходить через центр тяжести головы, поэтому она получает как поступательное, так и вращательное ускорение.

Еще более 200 лет назад Потт, известный хирург из Лондона, отметил связь между контактной зоной при ударе и последующим повреждением головного мозга [3]: “Исходя из моего опыта и наблюдений я заключил, что самочувствие для большинства пациентов, подвергшихся удару по голове в (или под) лобной части черепа, лучше, чем для тех, которые получили удар в другой части черепа. Нельзя ли это утверждение сделать основой для исследования?”

В работах Холбауна [4] отмечается, что вращательное движение головы является более опасным с точки зрения риска повреждения головного мозга. Такое утверждение основывается на гипотезе о несжимаемости мозговой ткани и, следовательно, поступательное ускорение неспособно вызвать ее значительное деформирование (повреждение). При вращательном ускорении нет препятствий для сдвиговых деформаций, и относительные смещения слоев мозговой ткани следует

рассматривать в качестве главной причины существенного повреждения головного мозга. Такой эффект вращательного ускорения отражен на демонстрационной модели (см. рис. 1).

В более поздней экспериментальной работе [5], проведенной на приматах, показано, что комбинация поступательного и вращательного ускорения головы в плоскости вращения вокруг затылочного спинного хребта (венечная плоскость), которая в некоторой степени аналогична боковому удару по голове, является более повреждающей головной мозг, чем аналогичное ускорение в сагиттальной плоскости (плоскость лобового удара). Такой эффект зафиксирован в некоторых автомобильных авариях [6]. Однако в исследованиях, приведенных в [7], отмечается, что связь между ударами в венечной и сагиттальной плоскостях может иметь более сложный характер по сравнению с общепринятым.

Для моделирования вышеуказанных ударных воздействий, с учетом вращения частиц головного мозга, наиболее эффективным является рассмотрение проблемы с точки зрения нелинейной механики сплошных сред, привлекая при этом численные методы решения задач ударной динамики.

При таком подходе правильный выбор расчетной схемы, модели (или разработка новой) поведения мозговой ткани является одним из главных звеньев математического моделирования.

Разработанные на сегодня модели поведения мозговой ткани отражают неоднородность, анизотропность и нелинейность. Они строятся в основном на принципе малых деформаций и упругом или вязкоупругом поведении ткани. В некоторых случаях рассматриваются двухфазные модели.

Как известно, головной мозг представляет собой гетерогенную структуру. На механические свойства мозга могут оказывать влияние такие компоненты, как: тканевый компонент, механические свойства которого определяются свойствами мембран клеточных элементов, нервных волокон, а также сосудистых стенок; компонент крови, влияние которого на механические свойства осуществляется через изменение объема в сосудах мозга и уровня внутрисосудистого давления; компонент тканевой воды – через количество экстра- и интрацеллюлярной жидкости, а также уровень тканевого давления; компонент жидкости – через ее количество в желудочках мозга.

Трудности работы с таким объектом, как головной мозг, есть причина того, что его механические свойства до сих пор изучены недостаточно. Хотя показано [8], что упругие свойства живого и мертвого мозга не отличаются сильно, этот факт не может объяснить изменение механических свойств в различных физиологических состояниях организма.

Учитывая вышесказанное, в структуре головного мозга выделим церебральные желудочки, которые наполнены жидкостью и вносят существенную неоднородность в анатомию мозга.

В данной статье по отдельности моделируются вращения головы в венечной и сагиттальной плоскостях при импульсном воздействии. В обоих случаях зафиксировано явление понижения сдвиговых деформаций, указывающее на природную защиту головного мозга от неблагоприятных сдвиговых деформаций мозговой структуры.

Данный факт представляет также интерес с точки зрения бионики и может быть взят на вооружение при создании технических систем.

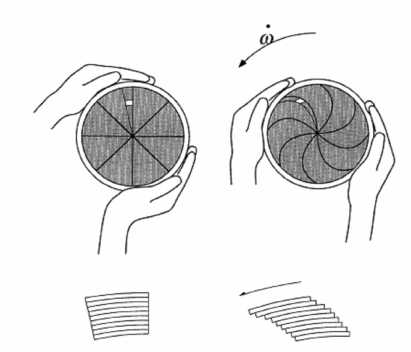
Рис. 1. Эффект сдвиговых деформаций при вращательном ускорении сосуда с наполнителем

Основные соотношения математической модели

В предложенной математической модели использованы основные соотношения кинематики деформирования и ударной динамики сплошных сред, приведенные в [9].

Напряжения для упругих и гиперупругих материалов не зависят от пути деформирования, следовательно, они не рассчитываются через инкрементальную теорию (последовательные приращения).

Для моделирования поведения ткани головного мозга выбрана наиболее простая модель нелинейного гиперупругого материала – модель Блатса и Ко, где для описания кинематики малых перемещений, но больших сдвигов используется второй тензор напряжений Пиола–Кирхгофа [10]:

S ij = G

V ^ v

- V ( 1/^{(1 - 2} ^ )) § j

где G – сдвиговый модуль упругости, V – относительный объем элементарного деформированного параллелепипеда, ? – коэффициент Пауссона, Σ ij – правый тензор деформации Коши–Грина:

v _ 5xk 8xk “                 , ij   8X, 8Xj где δij – символ Кронекера.

Напряжения Пиола–Кирхгофа преобразуются в напряжения Коши по формулам [10, 11]:

„ _xox, ^CT j _{a a} Ski ^. P о 8 x k 8 x i

Компоненты вектора перемещений определяются как: u, = x, - X,, где Xi и xi – лагранжевы и эйлеровы координаты, соответственно.

Используя 8-узловую конечно-элементную аппроксимацию и минимизируя невязку по Галеркину, получаем полудискретное уравнение метода конечных элементов с нелинейной, зависящей от времени и решения правой частью:

mV = f b - Ef в ^T S ij ( s ij ) dV e ,                           (1)

e Ve где M- диагональная матрица масс с размерностью [3Nx3N] в общем случае (N- число узлов конечных элементов сетки), FВ – вектор внешних и массовых сил, B – матрица производных от функции формы, Ve – объем конечного элемента, vt – столбец узловых ускорений.

Для интегрирования по времени уравнения (1) используем условно устойчивую, явную, центральную конечно-разностную схему, которая оказывается наиболее эффективной при надлежащем выборе шага интегрирования по времени и при этом позволяет уловить резкие изменения основных полевых функций:

vtn = M -1 . Fn, vn+1 / 2 = vn—1 / 2 + / A tn, un+1 / 2 = un + vn+1 / 2 a tn+1 / 2^ A tn+1 / 2 =(a tn +A tn+1)/2.

В качестве достаточного условия устойчивости решения используем условие Фридрихса–Леви–Куранта [12]:

A t h/C ,

Ah = min (A hi); i = 1,..., N, где Δh – радиус описанной окружности для каждого элемента, C – адиабатическая скорость звука в материале.

Результаты моделирования и выводы

Для проведения вычислительного эксперимента используем данные компьютерной томографии для построения геометрии головы взрослого человека (см. рис. 2) по основным ее размерам (без челюсти).

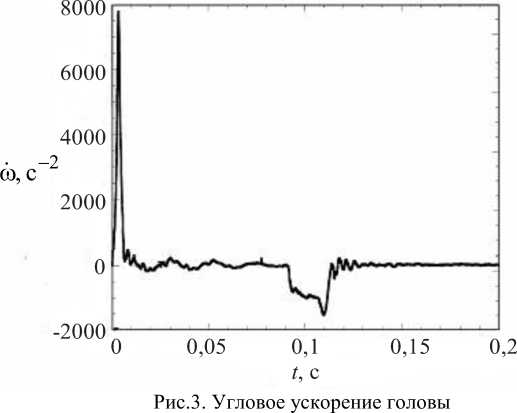
Характеристика гиперупругого материала мозговой ткани в виде модуля сдвига G = 1100 Па, распределение начального импульсного углового ускорения (b ( t ) (рис. 3), а также результатов эксперимента в лабораторных условиях (рис. 4) на гелиевом аналоге мозговой ткани, использованы из [13].

Расчеты проводились по отдельности для вращения головы вокруг двух взаимно перпендикулярных осей (рис. 5).

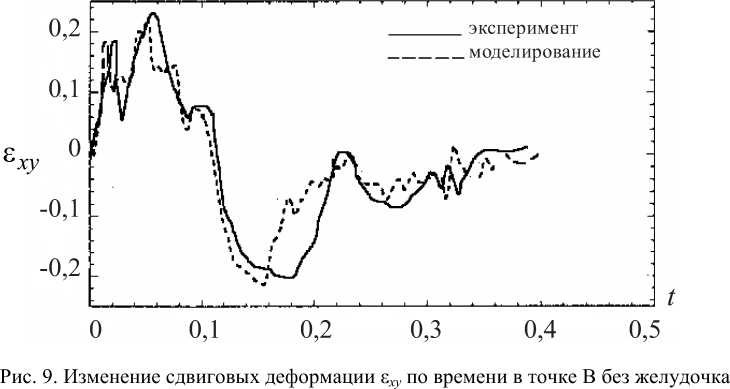
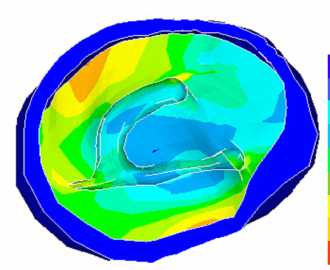
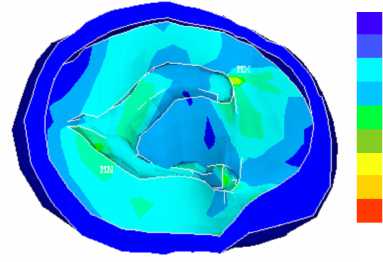
На рис. 6–9 приведены изменения сдвиговых деформаций над и под желудочковой окрестностью в случаях наличия желудочка с жидкостью и без него при вращении головы в венечной плоскости. Рис. 10 отражает картину эквивалентных деформаций в венечной плоскости головного мозга для моментов времени t = 0,026, 0,052, 0,3 с.

Приведенные графики показывают, что церебральный желудочек с жидкостью снижает уровень сдвиговых деформаций. Аналогичные графики получаются и при вращении головы в сагиттальной плоскости.

Полученные результаты свидетельствуют, что при моделировании такого рода задач большое значение имеет учет неоднородной структуры головного мозга. Эти неоднородности могут быть в виде составных частей самого мозга: цереброспинальных желудочков, крупных кровяных сосудов мозга и т.п.

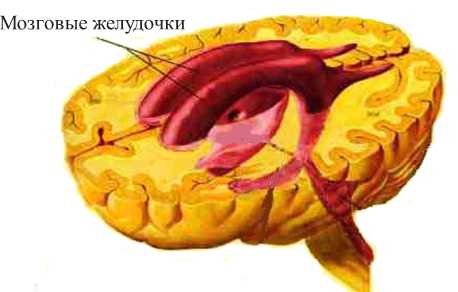
Рис. 2. Мозг в разрезе

Жидкость     Гель

Рис. 4. Экспериментальная установка

Такой подход с точки зрения механики деформируемых сред дает возможность определить максимальные деформации, разрушающие волокна головного мозга и, соответственно, начальные условия возникновения этих деформаций. При этом учёт особенностей анатомии головы (включая ее размеры соответственно возрасту человека и т.п.) дает возможность пересмотреть (скорректировать) используемый на практике критерий повреждаемости головы, полученный в результате испытаний на манекенах [14]:

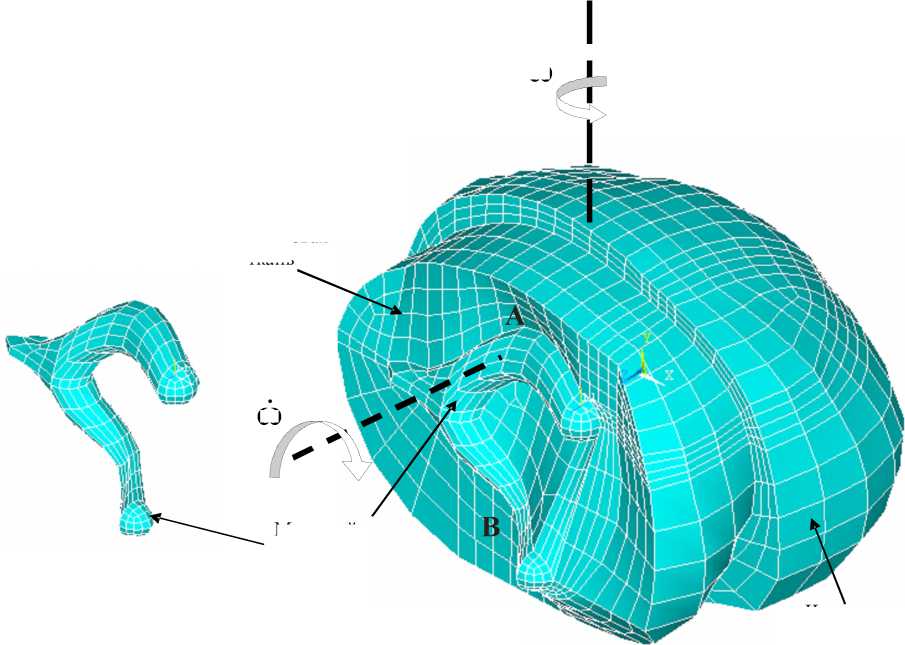
ω

Мозговая ткань

ω

Рис. 5. Конечно-элементная модель головы в разрезе

Мозговой желудочек

Черепная кость

0,2

0,1

^c xy

-0,1

-0,2

эксперимент моделирование

t

0        0,1        0,2       0,3        0,4       0,5

Рис. 6. Изменение сдвиговых деформации ε _xy по времени в области под черепной костью (т. А) с желудочком

2,5

HIC =

1      1 2

-----Г J a ^{( t} d    ^{( t} 2 ^- t 1 ) , t 2 - t 1 t 1

где a ( t ) – линейное ускорение головы как ускорение материальной точки.

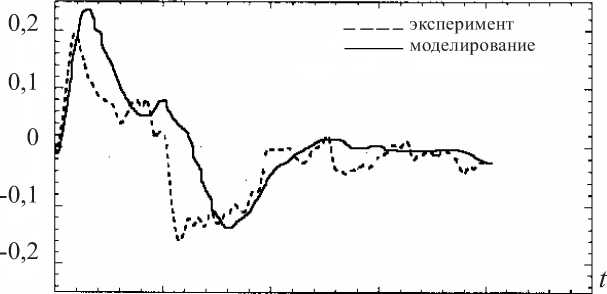
0        0,1        0,2       0,3        0,4       0,5

Рис. 7. Изменение сдвиговых деформации ε _xy по времени в области под черепной костью (т. А) без желудочка

0,2

0,1

ε xy

-0,1

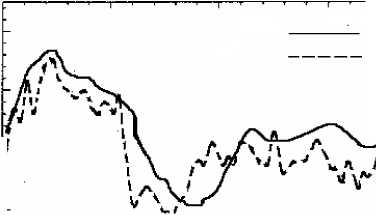
fj\ эксперимент моделирование

-0,2

t

0        0,1        0,2       0,3        0,4       0,5

Рис. 8. Изменение сдвиговых деформации ε _xy по времени в точке B с желудочком

t = 0,026

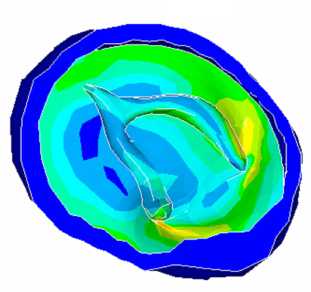
t = 0,3

0,000005

0,152517

0,305028

0,457539

0,610050

0,762561

0,915073

1,068000

1,312000

t = 0,052

0,000004

0,145303

0,290602

0,435902

0,581201

0,726500

0,871790

1,017000

1,251000

0,000001

0,118550

0,355650

0,474190

0,592750

0,711300

0,829850

0,950000

1,067000

Рис. 10. Эквивалентные деформации в венечной полости