Derivation and Comparative Study on Centroid Ranking Value of TrIFN and Apply on Fuzzy Geometric Programming

Published Online March 2016 in MECS

• I.    Introduction

  Ranking fuzzy numbers has been an indispensable area of research especially for its applications in decision making analysis to represent uncertain value. Ranking fuzzy numbers started in 1976 when Jain [9] proposed a ranking fuzzy numbers for decision making in the presence of fuzzy variables by representing the ill-defined quantity as a fuzzy set. Bortolan and Degani [5] reviewed some of ranking methods for ranking fuzzy subsets. Chen [17] suggested ranking fuzzy numbers with maximizing set and minimizing set. Delgado et al . [3] showed a procedure for ranking fuzzy numbers. Chen and Lu [5] suggested an approximate approach for ranking fuzzy numbers based on left and right dominance. Here we tries to incorporate the centroid based ranking method with Trapezoidal Intuitionistic Fuzzy Number (TrIFN). Atanassov [1,2] first introduced the concept of

intuitionistic fuzzy set(IFS) characterized by a membership function and a non-membership function, which is a generalization of the concept of fuzzy set [6] whose basic component is only a membership function. In real life application non linearity in optimization technique is biggest challenge. Geometric programming is one of the best ways to deal with such situation. But non linear optimization in real life can be uncertain and situation oriented, due to changing the environmental components. Here intuitionistic trapezoidal fuzzy system (TrIFS) is used to deal with such uncertain nonlinear environment. Coefficients of decision variables in the objective function, the constraint coefficients, and the right-hand sides of geometric programming problem are taken as TrIFN. Using centroid ranking method at first we generate centroids along x axis and y axis of individual TrIFN. After that we calculate the ranking value from two centrioids. In this way we get individual ranking value of all TrIFNs. These ranking values can be used in geometric programming problem for making decisions.

• II.    Preliminaries

• 2.1.    Definition

Intuitionistic Fuzzy Set : Let a set X be fixed, A is an IFS in the form

A = {< x, ц (x), v (x) >: x e X}

AA ц (x) is degree of membership and v (x) is a degree AA of non-membership. Where

• i)    0 < ц (x) < 1

A

• ii)    0 < V (x) < 1

A

• iii)    0 < Ц (x) + V (x) < 1

• 2.2.    Definition

AA

Intuitionistic Fuzzy Number: An IFN A is defined as follows:

• i)    An intuitionistic fuzzy subset of the real line.

• ii)    Normal, i.e., there is any x_o e R such that

M ⁽ x ) = 1( v ⁽ x ) = 0)

A ^A

• iii)    A convex set for the membership function ц ( _x )

A ц (x) (2x + (1 - 2)x2 )> min^ (x), ц (x2 ))Vx, x2 e R, 2e[0,1] A                                             AA

• iv)    A concave set for the non-membership unction v ( x )

A ц (x) (2x + (1 - 2)x2) < max(ц (x), ц (x2)) Vx, x2 e R, 2 e [0,1]

III. Centroid based Ranking Method

Let A = ([ a , b , c , d ],; w , u ) be a TrIFN, which has been shown in Fig-1. In order to find out the centroid of TrIFN, the area under the membership and non membership function has been considered together. First of all the whole TrIFN has been split into five rectangles: AGHB, BHKC, KJDC, DJIE and EILF.

Now, the centroid point has been determined by using the formulae

J xf ( x ) dx J f ( x ) dx

J yg ⁽ У ) dy J g ⁽ У ) dy

2.3. Definition

Let A is a TrIFN and is represented as A = ([ a , b, c, d ],[ a ', b , c , d ‘ ]; w, u )

where 0 <  w < 1;0 <  u < 1; w + u < 1; a , b , c , d , a^f, d ' e R

Its membership and non-membership functions are defined as follows:

( x — a ) ⁽ b ^{- a} )

w , a <  x <  b

M a ^{( x} ) = *

( d — x ) ( d — c )

w , c <  x <  d

0,    otherwise

V A ( x ) =

( b — x ) + ( x — a') u   ,

(b - a')      ,a u,         b < x:

Where the specific region bounded by continuous function f ( x ) and g ( y ) respectively.

The required centroid point is ( X , Y ) .

• 3.1.    Mathematical derivation of centroid point

From Fig-1 we get

• i)    fL:[a,b]->[0,w] and fR:[c,d]->[0,w]  are left and

right part of membership function of TrIFN A respectively.

• ii)   gL:[a,b]->[0,u] and gR:[c,d]->[0,u] are left and

right part of non membership function of TrIFN A respectively.

• iii)    h_L:[0,w]->[a,b] and h_R:[0,w]->[c,d] are the inverse function of fL and fR respectively

• iv)    k_L:[0,u]->[a,b] and k_R:[0,u]->[c,d] are the inverse function of gL and gR respectively.

From equation (1) and (2) and representing TrIFN as A = ([ a , b , c , d ],; w , u ) , we get

( x — c ) + ( d' - x ) u

, c

( d'- c )

0, otherwise

For sake of simplicity, throughout this paper we have considered a = a ‘ , d = d'

Symbolically, then TrIFN has been represented as

A = ([ a , b , c , d ],; w , u )

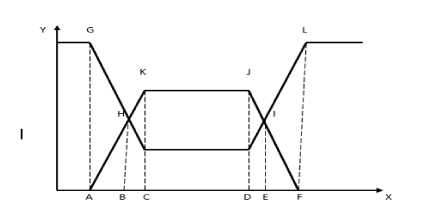
Fig.1. Trapezoidal Intuitionistic Fuzzy Number

(x - a)        (d - x)        (b - x) + (x - a)u      (x - c) + (d - x)u k = b^ w, fR = d^ w, gL =   (b - a)   ’gR =   (d - c)

h = a ₊ (b - a)y ,   = d - (d-Ф ,   = ^{( a} - b ) ^y + ( b ^{- au} ) ,   = ⁽ d ^- c ) y + ⁽ c ^{- du} )

L           w ^R          w      L         (1 - u )      , ^R         (1 - u )       J

From Fig-1 we get

( aw - au+b ) w - u+1                  b xx =   J   xgLdx + J   xfLdx + a                 ( aw-au+b)

w - u + 1

( dw - du + c )

J xwdx + b

J xg R dx

( dw - du + c )

x ₂

( aw - au + b )

w—u + 1

J   gLdx +

a

b

J   ^fL dx +

( aw - au + b )

>

J wdx + b

( dw — du + c )

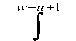
d fRdx + J gRdx

( dw — du + c ) w — u + 1

Derivation and Comparative Study on Centroid Ranking Value of TrIFN and

Apply on Fuzzy Geometric Programming

Integrating x we get

x1 = g L

x ²

( aw — au + b ) w — u + 1

+

+

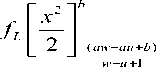
a

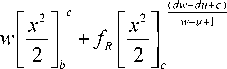
⁺ g R

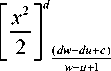
f , 3 (aw — a и + b)² ) И’ О------

1 ( ( И' — И + 1 )     )

2             b — a

( , aw — a и + b Л a w о — ------------

_ _____V_______ w — ZZ + 1   ) b — a

( (d w — d и + eV и- ---------------7

,     <      , x , 1 I (w - » + 1)")

+ w (c - b) + — ----- ¹-------T²--------

, , . x w — a и A- bV

( - b + a и )  —-----------^— — a

1 _______________ (   ( w — м + 1) ___________

2                  a — b

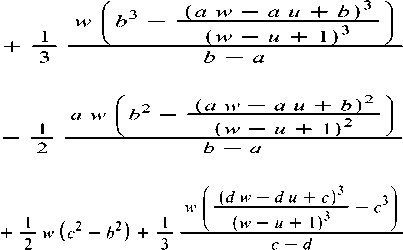
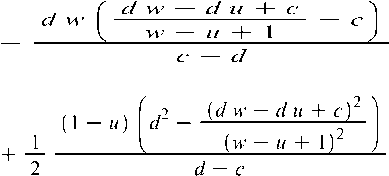
d w — d и X c w — и + 1

Putting the values of x and x at equation (3), we get

X

A

x ₁

x

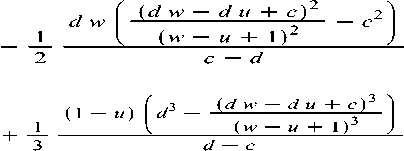
^d w — б/ м + c)² (w — и A- 1 )²

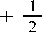
( — c + d и)

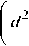
Integrating x we get

( aw — au + b )

x2 = gL [ x ] a w- u +1  + fL [ x ] ( aw — au + b ) + w—u +1

(dw — du + c )

w [ x ] b + fa [ x ] c w—u+1  + gR [ x ] (dw—du+c) = w—u +1

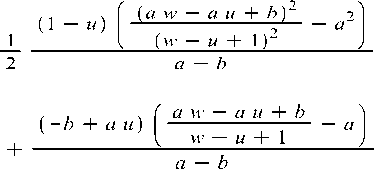
• ,,     , f (aw — a и + bA 3)

• (1 — zz)   -------------------r2

• 1    ____________ (    (И’ — zz + 1 ) ____________

, , ,        (a w — а и X bY

( -b + a u) --------------a

• 1__ ( (w — и + 1 )² _________

, 3     (a w — a и + b )³

w b---

• 1     ________ (w — и X 1) ____

• 3             b — a

( , 2 (aw — a и + b)² ) a w b — ---------------

_ 1 v (w — zz + 1     )

• 2             b — a

  

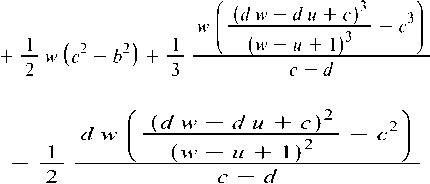
  X

  
  

  X

  
  

  d и'

  
  

  ⁺ T

  
  

  х

  
  

  И'

  
  

  W

  
  
  
  

  c — d

  
  
  
  

  х

  
  

  w

  
  

  d w

  
  
  
  

  (« w — а и + b)²

  (w — и А- 1)² а — b

  
  

  w

  
  
  
  

  w — u +1

  
  
  
  

  У1 = J У ( ^h R - ^h L ) dy ⁺ J yddy - J yh R dy - J yk R dy

  
  
  
  
  
  
  
  

  w — u +1

  
  

  ,      , i i >2 (d и¹ - d и + )

  (-c + d и) d---

  ___________(________ (w - » + I)² d - c

  
  
  

  +

  
  

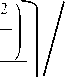
  J yh_Ldy +

  
  

  w

  У 2 = J ⁽ h

  
  

  +

  
  
  
  
  
  

  J yk L dy — J aydy

  w 0

  w—u + 1

  
  

  1          w — u + 1             1

  — h_L ) dy + J ddy — J h_Rdy — J k_Rdy

  
  

  J h_Ldy +

  
  
  
  

  w — u + 1

  
  
  
  

  J k_Ldy —J ady w 0

  
  

  a w — a и + b

  -------------- — a

  
  
  
  

  a — b

  
  

  Integrating y we get

  
  

  ,2      (<7 И' — (Z I/ + 6 )²

  
  

  b — a

  
  

  . Г у ² 1 '

  У 1 = ^{( h}R ^{— h}L ) 4" - ² J o

  
  

  w

  
  

  П 2 1 ^{+ d}

  
  
  
  

  J o

  
  

  ^— h R

  
  

  w

  ²    w — u + 1

  у

  ² J o

  
  

  —

  
  

  k_R

  
  

  y ² 2

  
  

  w

  
  

  w — u + 1

  
  

  ,2 (а И' — a u + 6 )²

  
  

  b — a

  
  
  
  
  
  

  + h

  
  

  y 2

  ² J o

  
  

  w

  
  

  w—u + 1

  
  

  + k

  
  

  y ² 2

  
  
  
  

  — a

  
  
  
  

  =

  
  

  d — с

  И'

  
  

  b — а

  И'

  
  
  
  

  w

  w—u + 1

  
  
  
  

  y²

  ² J o

  
  
  
  
  
  

  X

  
  
  
  

  (d — с) и"

  (w — и + 1)³

  
  

  d и’²

  
  

  ,2 ^d w — d и + с)²

  _______ (w — н + 1 )²  ₂

  d — c

  
  

  2 (w — и + I)²

  
  
  
  

  (                ³ J

  (d~c) 1-—^---

  _______ (w — н +

  1 — и

  
  

  (c - du) 1 -

  
  
  
  

  , d w — d и + c

  d--:—

  
  
  
  

  1 - и

  
  

  + 1   (6 - а) и"

  ³ (w - и + I)

  
  

  d — c

  
  
  
  

  a w

  
  
  

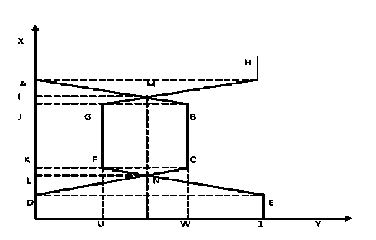
  Fig.2. Inverse Function of TrIFN

  
  
  
  

  (.а — b)

  
  

  (b — а и)

  j__

  
  

  Integrating y we get

  
  
  
  

  з

  
  

  1 —

  
  

  ,2

  
  

  From Fig-2 we get

  
  

У 2 = ^{( h} R ^- h L ) [ У ] o w + d

w

^- h R [ У ] o w - u + 1 - k R [ У ] - w-w - u + 1

J a w²

^ (w — и + 1 )²

w

^{+ h}L ^[ У ^] o w '' + '

^{+ k}L [ У ] w ^- a [ У ] o1 w — u + 1

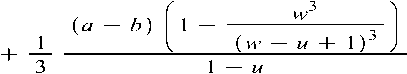
b-a } 2 , ,          , , t/w

---- w -Vaw-aw-Vd--- w                    w-и+1

1 (d — c) w

2 (w — и + I)²

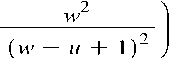
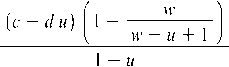
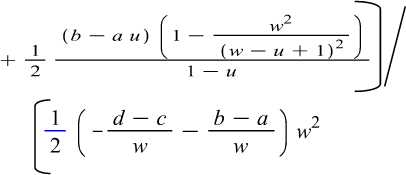
a w w — и + 1

+ dw - aw + d -

dw w - и + 1

(

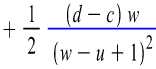
(^-^) 1---7

1 Vb - a^w                 у (w - i/ + 1)

2 (w - и + I)2    2

^b — a u^ 1 —

w

1 — и

— a

Putting the values of y and y at equation (3), we get

1     (,b — a) w

(w — и + I)²

Y a = ^У = y ₂

If d — c b-a 'l з , 1 , ,   ,2,1,,

-----w + — (d - a) w + — d + 3 v w w )       2               2

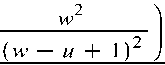
1    (б/ — c) w2

(w — и + I)³

^b — a u^

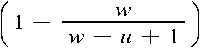
1 d w²

(w - и + I)²

(w - w + l)j y

1 - и

(c-du) 1--- j(w - w + I)2 , 2

1    (^ - a^ w²

^ (w - и + I)³

3.2. Centroid Based Ranking function

The ranking function of the TrIFN A = ([ a , b, c, d ],; w, u )      is      defined      as

22, which is the Euclidean centroid               A      A distance from the circumcenter of the centroids and the original points.

Now from equation (6) and (8) we can generate centroid based ranking value of A = ([ a, b , c, d ],; w, u ) , which is R_centroid ( A )

• IV.    Comparative Study of Centroid Ranking Method With Other Ranking Approaches

• 4.1.    Numerical Example

Here we try to compare centroid based ranking approach with a) Wu and Cao ranking method b) Jianqiang and Zhong ranking, using two numeric examples and conclude to a particular decision.

• Example 1:

Suppose TrJFN

A = [(0.63,0.75,0.33,0); 0.65,0.2]

В = [(0.62,0.75,0.329,0); 0.63,0.21]

dU,r⁺) = - [1(1 + ^ - u_L)a - (1 + w₃ - u₂). 11

+|(1 + wL - ujb - (1 + w2 - ид). 11

+|(1 + Wi - ujc - (1 + w3 - U2). 1|

]

Where

And

If

Here

d(Ar+) = 0.35 and d(B,r+) = 0.35

So,                    or A=B

But putting the value of A and B at equations (5), (6), (7) (8) we get

X_A = 0.2547 Fj = 0.357 Я₅ = 0.2475

F3 = 0.357

So, A>B

• Example 2:

Steppose TrIFN

A = [(0.56,0.74,0.80,0.9); 0.5,0.5]

В = [(0.50,0.70,0.35,0.95); 0.5,0.5]

sGO = /GO * (w — u) hGO = /GO * (w + u) Where

Л = [(a, & с, Д^и]

Here

HGO = 0.375, H® = 0.375

So, A≈B

But putting the value of A, B at equations (5), (6), (7)

• (8)    we get

  Хд = 0.7236 ^ = 0.3715 Ay =0.7146

• 4.2.    Discussion

Аг = 0.3542                  "

So, A>B

From example1, using Wu and Cao ranking method, we observe that, these two TrIFNs (A, B) are not comparable, but using centroid ranking method two TrIFNs (A, B) can be compared as A>B.

Similarly in example2, using Jianqiang and Zhong ranking method we observe that ,these two TrIFNs(A,B) cannot be compared, but using centroid ranking method two TrIFNs(A,B) can be compared as A>B.

From these examples it is clear that, for deriving the ranking result, centroid based ranking method is one of the best approaches because this method gives ranking result correctly and overcomes the drawbacks of the existing methods (Wu and Cao, Jianqiang and Zhong) .For this reason we try to incorporate this approach in nonlinear uncertain environment for getting better decision making results. Fuzzy geometric programming is one of the significant areas to take decision at most uncertain real life situations. Below we try to implement geometric programming and its duality in fuzzy environment and using centroid based ranking method we generate ranking values of TrIFNs and using them we generate a mathematical derivation.

• V.    Centroid based ranking value in Fuzzy Geometric Programming

• 5.1. Generalized equation of Fuzzy geometric programming

Here we are taking the coefficients of objective function,constrains and right hand side of constrains as TrIFN.

Min f (')=£caj-iix.a0i j=1

Subject to constrain gk (x) = ^^^ ckj Ini xia ^^ b j =1

Or

Nk gk(x) =  £ ckj-П xkj --1

bi              bi j=1

Where

Coj (j = 1,2,,

C_y( k = 1,2,........, m ; j = 1,2,........., N k )

b ( i = 1,2,.........., n ) are TrIFN.

5.2 Dual form of Fuzzy geometric programming equation with centroid approach

Max

m  N k ( R    ..Cc. ) NN    3 kj

v ( 4 )= nn   centred ^{( kk} ) Z 4

к = 0 j = 1 ^      ⁴      l = 1     J

Where R_centroid ( c_kj ) = Centroid based value.

A n + 4 02 + 4 ,3 = 1            )

⁴ 01 ^{+ 4}03 - ⁴11 = ⁰

4 )2 + 4 ,3 - 4 1 = 0             >    ⁽¹2)

⁴ 01 ^{+ 4} 02 ^- ^ 11 = ⁰

4 ,, - 0, 402 - 0, 4 ,3 - 0, 4 1 - 0

Subject to constrain                           (10)

N0          m Nk z j1, Z Z akij^kj =0, 4 -0

j = 1             k = 0 j = 1

Solving equations (12) we get

where i = 1,2,.........., n ; j = 1,2,........., N_K ;

k = 1,2,, m          -

VI. Numerical Example

Putting the values in equation (11) we get

1   1   12

( 12.333 ) 3 ( 19.539 ) 3 ( 30.291 ) 3 ( 3.554 ) 3 =43.48

Example:

Min f (x) = (2,3,4,6; 0.4,0.6) x,x3 + (4,6,7,9; 0.3,0.7) xx. + (8,9,10,12; 0.5,0.5) xxx2

Subject to

(50,70,80,90; 0.8,0.2) x- ^-1 x ₂1 x ₃^-1< (10,20,25,30; 0.6,0.4)

Where x , x ₂, x ₃ - 0

Where x , x ₂, x ₃ - 0

So the minimum value of f ( x ) =43.48

From 4i = ^2 = 4з = ^ and 41 = "^ we get x = 1.6, x2 = 1.008, x3 = 2.476

So,

Min f (x) =43.48 and x = 1.6,x2 = 1.008,x3 = 2.476

For TrIFN A = ([ a , b , c , d ],; w,u )   , we have

R centroid ( A ) = X^XA ² + Ya²

Here c^ = (2,3,4,6; 0.4,0.6)

c 02 = (4,6,7,9; 0.3,0.7)

c ₀₃ = (8,9,10,12; 0.5,0.5)

c_n = (50,70,80,90; 0.8,0.2) / (10,20,25,30; 0.6,0.4)

Using equations (⁶⁾, ⁽⁸⁾ and Rc_entroM ( A ) = j X a ² + Ya²

we can generate

R centroid ( ^ 01 ) = 4.111 R_ce nroid ( ^2 ) = 6.513

R centroid ( -   I = 10.097      R centroid ( c _H) = 3.554

"⁴ Г6.513                '

I    --—( Й 01 + 4 + Л „3)

4.111,2

v ( A ) =        ( A 01 ⁺ A )2 ⁺ 4 )3)

"⁴ Г3.554

10.097

₂    ^{( 4} 01 ^{+ 4} 02 ^{+ 4} 03 )

⁴ 03                          .

A 1

L ^ n

Subject to

• VII. Conclusion

In this paper we try to analyze one of the important ranking approach, which is centroid based and apply it on Trapezoidal Intuitionistic Fuzzy Number(TrIFN).We choose TrIFN, because of its both membership and non membership functional support. Any real life situation is combination of possible and non possible occurrence of incidents, which can be represented by TrIFN, in better way. Using centroid based ranking approach we generate single quantitative value from interval based TrIFN, which is applied on geometric programming problem. For working on real life non linear environment geometric programming is a better approach and using TrIFN with centroid based ranking method on geometric programming gives perfect decision making result. Here our main aim is to deal with situation oriented real life decision making problem with non linear uncertain mathematical analysis in presence of ranking approach.