Description of some weighted exponential classes of subharmonic functions
Бесплатный доступ
The role of subharmonic functions in such sections of analysis as complex and real analysis is very significant. Such classes of functions are closely related to analytic harmonic functions and make an important contribution to the general theory of potential and mathematical physics. In the works of R. Nevanlinna and W. Heiman, parametric representations of subharmonic classes in the plane of functions, whose characteristic has a power growth at infinity, are obtained. The question of whether similar representations are true for weighted classes that admit a stronger growth at infinity (for example, the exponential growth) arises in the theory of entire and meromorphic functions. In this article, classes of subharmonic functions with Nevanlinna characteristic that is summable with exponential weight in a complex plane are introduced for consideration, and the representing measures of functions of such classes are studied. When proving the results, methods of complex and functional analysis are used. An important role in the study is played by potentials based on the factors of the modified Weierstrass product. The proof of the main result is based on the use of auxiliary assertions formulated in the form of lemmas.
Subharmonic function, harmonic function, representing measures, thenevanlinna's characteristic
Короткий адрес: https://sciup.org/147158968
IDR: 147158968 | УДК: 517.53, | DOI: 10.14529/mmph180101
Текст научной статьи Description of some weighted exponential classes of subharmonic functions
Let C be the complex plane. SH ao ( C ) ( о , a are positive numbers) be the class of subharmonic
+^
functions u in C such that
j T ( r , u ) e -o r dr <+^ , where T ( r , u ) is the Nevanlinna’s characteristic of
1 П + subharmonic function u, that is T (r, u ) = — I u+(r cosф, r sin^) dф, u += max (u ,0) (see [1-4]).
-П
In complex and real analysis, potential theory and mathematical physics the value of subharmonic functions is very significant (see [1–3, 5]). In the works R. Nevanlinna and W. Hayman (e.g., see [1]) the obtained definition of a class of subharmonic in the plane of the functions, the characteristics of which have exponential growth at infinity. The question of whether faithful same parametric representation for the weight classes, allowing for stronger growth at infinity, say exponential growth, occurs in the theory of entire and meromorphic functions (see [6]).
This paper studied the representing measures of the functions of class SHao (C), as well as the necessary and sufficient condition for such measures.
Statement of the main result
Let о , a > 0 , z, Z e C , Z * 0, P (| Z ) = max 0\£ \ a ,1 ] , where [ a ] is the integer part of a real number a .
is a factor of the modified product by K. Weierstrass (see
V
[7, 8]).
Математика
Theorem 1. Let u e SH ao ( C ) , Ц is representing measure of a function u. Then ц satisfies the condition:
+^
J
n ( t ) e
—
t a
m“
— dt < +^ ,
where n ( t ) = ц ( Dt ) , | z | < t.
The opposite is also true: let ц is some non-negative Borel measure in C, satisfying the condition (1) , then it is possible to build explicitly subharmonic function of class SH ao '( C ) , ^O : О > — + o e “ , for which ц will be a representing measure.
ea
Proof of auxiliary assertions
We require some auxiliary assertions for the proof of the theorem.
Lemma 1. Let y( R) is a non-negative monotonically increasing function, for which where a> 0. Then
+^
a
J ^ ( x ) e o dx <+^ ,
lim
R ^^
^ ( R^e —^ R a R^
= 0 .
+^
—I
°x' dx = 0.
Proof. The convergence of the integral (2) implies that the lim [ ^ ( x ) e
R ^+^ J
R
+^ +^
Let ^(R)= J y(x)e—ox dx. It is clear that ^(R)> ^(R) J e—ox dx . We find the asymptotics of the RR last integral by applying the L'Hospital's rule.
Therefore, lim
R ^^
+^
J e-° x a dx lim R r ^^ e ~oRa
^ ( R ) e —o R a
^ ''
= lim
R ^^
e —o R a
e a R a o R a 1 a e
R a — 1
—
= 0 . That is lim ^ ( R ) e —o R a R a — 1 = 0.
R -^^
oa
.
The lemma is proved.
Lemma 2. Let p ( x ) = e
—(
a
, x e R + , R + = { x e R : x > 0 } , £ x
~a . Then p ( x + £ x ) = e ^ x ) • e e ( x ) ,
where f( x ) = o [ — | when x ^+^.
V x 7
Proof. It follows easily from the following simple arguments. It is clear that f.\“ ao 1
V x 7 x V x 7
Then, e ^ ( x +£ x ) = e ^ ( x ) • e e ( x ), where в ( x ) = o V— 7
when x ^ +^ .
The lemma is proved.
Lemma 3. Let u is an arbitrary subharmonic function in C, while it admits a representation in the form:
u ( z ) = J ln| A p ( z, K ) d ^ ( K ) + h ( z ) ,
C
+^
z,Ke C, ^(K) is an arbitrary non-negative Borel measure in C, such that J n (r )= ^( Dr), c > 0, a > 0, h (z) is harmonic function in C, for which
+^ П
1 — П
n ( t ) e
—I
t a
c t a
—dt <+^ ,
Then u e SH a ^- ( C ) when VC : c'> — + c e a .
Proof.
Let V p ( z ) = J ln| A p ( z, K ) d^ K ) . Then u ( z ) = h ( z ) + V p ( z ) .
C
It is obvious that h ( z ) belongs to the class under consideration. We will show that Vp ( z ) also included in the class SH ac ‘ ( C ) for V С = C ( a ) > c .
We apply the estimate (see [1], p. 94):
К A p ( z, K )|< ;!
, K * 0, z, K e C .
Let's get that: u ( z ) < J K
C
To continue the evaluation of the function, we can partition the complex plane into sets:
p ( K I)
d ^ ( f ) .
+^
a k = { z e C :2 k < | z | < 2 k + 1 } , A o = { z e C : | z | < 1 } . Then u ( z ) < ^ J ^ k =0 A k K
Each of the rings A k is divided into small rings and we use Lemma 2.
Let 8 k j = { z e C :2 k + j 2~ a k < | z | < 2 k + ( j + 1 ) 2 — k a } , 0 < j < |^ 2 k ( a + 1 ) + 1 ^ , where [ a ] is the integer
Na part of the number a . Then Ak c Q 8k j , where Na = I 2k( ) I.
j =0 ’ L J
Therefore, z
A k
N
a
d*« ) < У J K
a
j = 0 8 k,j
By Lemma 2, we obtain
z
8 k , j
d ^ ( K ) < K *
p (I K * )
d ^ ( 8 k , j ) < 4*
K
It is obvious that
Therefore z
a k
p (I K 1 )
n ( 2 k + ( j + 1 ) 2 a k ) , where K is a point of 8 k j .
z
K
p (I K i)
a
d^(K)< Cу J
N a 8 , j + 1 z p ( t )
j =0 V ,
t
2 k + ( j + 2 ) 2 — a k
J
2 k + ( j + 1 ) 2 — a k
2 k + 1
n ( t ) dt < C J z k t
k
z t
n ( t ) dt , k = 0,1,...
p ( t )
n ( t ) dt .
Summing over k , we get:
Математика
+^
u
(-") 1t p (t) n (t) dt. Let us estimate the last integral. According to (5) we have that +^ j e - п +^ '°r j u+(re1<p) d^dr< C j e 1 °r j I I n(t)dtdr. -п Having established the convergence of the last integral, we prove the Lemma. To do this, imagine the inner integral as a sum: V/ V(t) erCAp(t) +~ / \p(t) I r j I — I n (t) dt = 11 +12 . er Let us prove the boundedness of the second integral by a constant, independently of r . Indeed, \ p (t) r I r — I = exp p (t) In —. r However, when — < e t rr In — < -1. Then exp p (t) In — < exp (-p (t)). p(t) = °'ta J, so p(t)>G'a-1. Therefore, exp(-p(t))< Ce °t . -G„at“/2а e< ~ , ° > °, n (t) < e t , +^ / pplt\ +“ +“ (A -ot“ r I r I f ( a -at “ , лГ” (t) e dt We estimate the integral. er >1=jf Consider the estimate for the integral I2 we get that +~ п +~ er/ pip (t) j e-a r j u+(re1^) dф< j e ^°r jf“| ” (t) dtdr . 1 -п 1 1 ^t1 To calculate the largest value of the function expp(t)(Inr - Int) on an interval [1;er] we put x = ln r и /(x, t ) = p (t)(x - ln t) . x-ln te« = 0. I 11 -1 That is lnr = ln tea , t = re a ta = rae-1 This point is the maximum point, therefore Y( x, t ) = Y x, re “ = p re a r \ p (t) r Because max ln r - ln re “ e then er j n (t) If 1 кt p(t) er ra e er ra raer dt = j n(t)eaedt =eae j n (t)dt 11 +^ j e— a ‘ ra raer +^ e ?ea j n (t)dtdr = j e — Ira err Г A j n (t)did = C1jn (t)dt —I • e I ra +^ +^ +- J a 1 —I e I га —-----n (er) dr. _ | ra—1 er In view of Lemma 1, we write that j n (t)dt< Cea(er) \a 1 1 ra—1. Using the last estimate, we clarify the values a , that ensure the convergence of the integral: +F —I J e I raer a ( f n(t)dtdr : ara — a(er)“-->0, raI a' — aea — ас ea The lemma is proved. Let us prove the auxiliary theorem 2. Theorem 2. Let u is an arbitrary subharmonic function in the class SHaa (C), Ц^) is an arbitrary measure of the function u, in this case ц( Dt) = n (t), 0 < t< +^. Then +^ j 1 n (t) е —( ta ata ---dt < +^. Proof. We integrate the integral by parts. Using the equality of Jensen for subharmonic functions (see [1]), it is enough to estimate the integral: +^ Г t I = j j 1 к 1 n (r)dr" e—atdt. r We integrate I by parts: a _ а t at t j n (r)dr" r +^ +^ +j e —at 1 — a ta j к 1 n (r)dr" r n (t)) , +--dt ta у According to Lemma 1, we have: +^ —( at r +^ taУ —(1—a) J a 1 ea ta—1 J--------+ n (t) dt By the hypothesis of the theorem I< C. It is clear that in 0 < a< 1 the theorem is proved, +” e—ata 1t Suppose a > 1. Then by Lemma 1: since from the condition (5) implies that +^ je — t1r1 „.a ea ta dt e "atata—1 r 7 dt 1t +- e—ata Because a>1, then J-----n(t)dt<+^ . 1t The theorem is proved. Математика The proof of the main result The proof of the direct assertion of theorem 1 follows from theorem 2. The validity of the converse follows from Lemma 3. That proves theorem 1 completely. From Theorem 1 directly follows Theorem 3. Let a> 0, SHaro = U SHao. Then class SHa„ coincides with the class of subhar-, о>0 , , monic functions in C, representable in the form u (z ) = J ln| Ap (z ,Z)\ d^(f) + h (z), where Ц is non-C negative measure in C, such that n(t) = ^( Dt), Dt ={ z: |z| < t}, and also satisfies the condition +^ ∫ 1 n(t)e ta „ a Ot dt < +^ for some a> 0, h an arbitrary harmonic function in C, for which there exists о > 0: J e~°ra J |h(re1^)d^dr< +~. 1 -П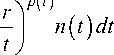
Список литературы Description of some weighted exponential classes of subharmonic functions
- Hayman, W.K. Subharmonic functions/W.K. Hayman. -Acad. Press, London etc. -1989. -Vol. 2. -591 p.
- Ронкин, Л.И. Введение в теорию целых функций многих переменных/Л.И. Ронкин. -М.: Наука, 1971. -432 с.
- Азарин, В.С. Теория роста субгармонических функций/В.С. Азарин. -Харьков: ХГУ, 1982. -73 с.
- Охлупина, О.В. Потенциалы типа Грина и интегральные представления весовых классов субгармонических функций: дис.... канд. физ.-мат. наук/О.В. Охлупина. -Брянск, 2012. -118 с.
- Брело, М. Основы классической теории потенциала/М. Брело. -М.: Мир, 1964. -215 с.
- Быков, С.В. О нулях целых функций с мажорантой бесконечного порядка/С.В. Быков, Ф.А. Шамоян//Алгебра и анализ. -Санкт-Петербургское отделение Института математики РАН им. В.А. Стеклова, СПб: Наука, 2009. -Т. 21, № 6. -С. 66-79.
- Shamoyan, F.A. Topics in the theory of spaces/F.A. Shamoyan, A.E. Djrbashian//Teubner Texte zur Mathematik . -BSB B. G. Teubner Verlagsgesellschaft, Leipzig, 1988. -Vol. 105. -P. 200.
- Шамоян, Ф.А. Введение в теорию весовых -классов мероморфных функций/Ф.А. Шамоян, Е.Н. Шубабко. -Брянск: РИО БГУ, 2009. -153 с.


