Design and Implementation of I-PD Controller for DC Motor Speed Control System by Adaptive Tabu Search

Published Online September 2017 in MECS

• I.    Introduction

  The proportional-integral-derivative (PID) controller was firstly proposed in 1922 by Minorsky [1] and firstly applied for industrial applications in 1939 [2]. The PID controller is a control loop feedback mechanism (controller) and widely used in industrial control systems.

This paper consists of seven sections. After an introduction given in section I, the related works of I-PD optimization are presented in section II. Details of ATS algorithms are illustrated in section III. The problem formulation of the PID and I-PD via the standard basic control loop is described in section IV. Application of the ATS to I-PD controller optimization for the DC motor speed control system is provided in section V. Simulation and experimental results are illustrated section VI, while conclusions are given in section VII.

• II.    Related Works of I-PD Optimization

The I-PD controller design optimization for DC motor speed control by the ATS can be represented by the block diagram in Fig. 1. The sum-squared error between R ( s ) and C ( s ) is set as the objective function J expressed in (1). J will be fed back to the ATS tuning block to be minimized in order to find the optimal I-PD parameters satisfying to the inequality constraints stated in (2), where

M p and E ss are maximum overshoot and steady-state error, K p , K i and K d are the proportional, integral and derivative

gains, respectively. Minimize	J = £ [ r (i) - c ( i ) ] 2 i = 1	(1)
subject to	M p <  10 %, E ss <  0.1%,
	10 <  K„ <  100, > p 300 <  K i <  600, 0.1 <  K d <  2.0	(2)

The use of AI search techniques to design the I-PD controller can be represented by the block diagram in Fig. 1. The cost function, J , the sum of absolute errors between R ( s ) and C ( s ) as stated in (1), is fed back to the AI tuning block. J is minimized to find the optimum I-PD controller’s parameters. In this work, the AI tuning block contains the ATS algorithm.

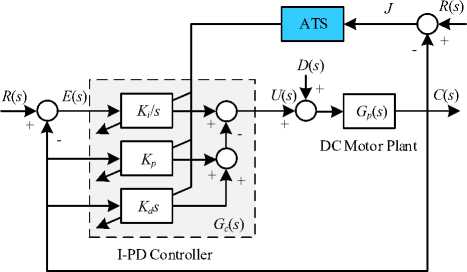
Fig.1. ATS based I-PD controller optimization.

• III.    Adaptive Tabu Search Algorithms

As a modified version of the original tabu search, the adaptive tabu search (ATS) is based on the neighborhood search approach. The ATS possesses the tabu list (TL), back-tracking (BT) and adaptive search radius (AR) mechanisms [19]. The TS is used to record the visited solutions. The BT is conducted to escape the local entrapment towards a new search path by using the data stored in the TL. Once a current solution is close to a local minimum, the AR is activated by reducing the search radius in order to speed up the search process. The algorithms of the ATS can be described step-by-step as follows:

Step 1. Initialize a search space, count and count max (maximum search round).

Step 2. Randomly select an initial solution x 0 from the search space. Let x 0 be a current local minimum.

Step 3. Randomly generate n solutions around x 0 within a certain radius R . Store the n solutions called neighborhood in a set X .

Step 4. Evaluate an objective function f( ■ ) of each member in X . Set x 1 as a solution that gives the minimum objective function in X .

Step 5. If f ( x ₁) <  f ( x ₀), put x ₀ into the TL and set x ₀ = x ₁, otherwise, store x ₁ in the TL instead.

Step 6. Activate the BT mechanism, when local entrapment occurs.

Step 7. Invoke the AR mechanism, when the search moves close to a local minimum by adjusting R = ^ R , 0< ц < 1.

Step 8. If the termination criteria (TC): count ≥ count max , or desired specifications are met, stop the search process. x 0 is the best solution found, otherwise update count , and go back to Step 2.

The ATS method [23, 24] is one of the most efficient AI search techniques. It is based on the iterative neighborhood search approach for solving combinatorial and nonlinear problems. The Tabu list, one important feature of the method that has first in-last-out property, is used to record a history of solution movement for leading a new direction that can escape a local minimum trap. In addition, the ATS method has two additional mechanisms, namely backtracking and adaptive search radius, to enhance its convergence.

The backtracking mechanism described in Step 6 is active when the number of solutions cycling is equal to the maximum solution-cycling allowance. This mechanism selects an already visited solution stored in the TL as an initial solution for the next search The round to enable a new search path that could escape the local deadlock towards a new local minimum. For the AR mechanism described in Step 7, it is invoked when a current solution is relatively close to a local minimum. The radius is thus decreased in accordance with the best cost function found so far. The less the cost function, the smaller the radius. With the two features, a sequence of solutions obtained by the ATS method rapidly converges to the global minimum. The ATS algorithm can be summarized by the pseudo code as shown in Fig. 2.

Objective function f ( x ), x = ( x 1 ,…, x d ) ^T ,

Search space Q, Tabu list (TL), Search radius R , Randomly generate initial solution x 0 within Q, Evaluate f ( x ⁰) via given objective function.

While (Termination criteria)

Randomly generate neighborhood solutions x ’ , Evaluate f ( x ’ ) via given objective function, Find the best neighborhood solution x ^*,

If f ( x ^*)< f ( x ⁰) Then keep x ⁰ into TL and update x ⁰ = x ^*, Otherwise keep x ^* into TL,

If local entrapment occurred Then activate BT,

If search closes to local solutions Then invoke AR to reduce R by adjusting R = цК , 0< ц <1.

End While

Best solutions found.

• Fig.2. Pseudo code of the ATS algorithm

• IV.    Problem Formulation

• A.    Basic Parallel PID Control Loop

A conventional feedback control loop with basic parallel PID controller is represented by the block diagram in Fig. 3, where G p ( s ) and G c ( s ) are the plant and the PID controller transfer functions, respectively. The PID controller receives error signal E ( s ) and generates control signal U ( s ) to controlled output C ( s ) and regulate disturbance D ( s ) referring to referent input R ( s ). The time-domain and s -domain functions of the PID controller is stated in (3)-(4).

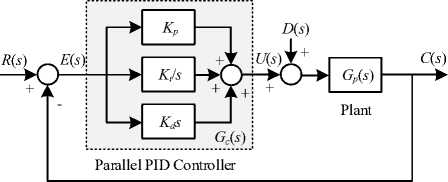
Fig.3. Conventional feedback control loop with basic parallel PID.

u (t )| PID = Ke (t) + KAe (t )dt + Kadet)(3)

dt

K

Gc (s ) pid = Kp + у + Kas(4)

(

K „ +--+ K s G„ ( s )

C(s) = I p s     d J pV’

^{R (} s )  1 + [ K_p + K^ + K a s J G p ( s )

V        s

The closed loop transfer function with basic parallel PID controller is given in (5). The main control objective is to make C ( s ) = R ( s ). By this objective, the controller continuously adjusts the control signal U ( s ) until the error E ( s ) is zero irrespective of the disturbance signal D ( s ). By using parallel PID controller, a step change in the reference input R ( s ) will cause an immediate spiky change in the control signal U ( s ). This abrupt change in the controller output is known as the proportional and derivative kick (or shortly set-point kick). This kick effects rapidly change the command signal to the actuator which controls the entire operation of the plant G p ( s ) [6]. To overcome this drawback, the I-PD controller is proposd.

• B.    I-PD Control Loop

The I-PD controller is one of the modified versions of the PID controller. It is developed to avoid the set-point kick and reduce undesirable overshoot. The feedback control loop with I-PD controller is represented by the block diagram in Fig. 4. Referring to Fig. 4, the integral part is still placed in the forward path, while the proportional and derivative parts are moved to feedback path of the control loop. By this scheme, only the integral term K i responds on the error signal E ( s ). An abrupt change in the reference input R ( s ) will not affect the proportional K p and derivative K d terms, since they work on the controlled output C ( s ). The time-domain function of the I-PD control signal is stated in (6) and the closed loop transfer function with I-PD controller is given in (7).

D ( s )

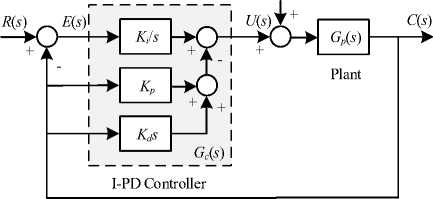
Fig.4. Feedback control loop with I-PD u (t)|I -PD = Kfe(t)dt 4KpC(t) + Kadc(t) J     (6)

V               at )

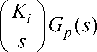
C ( s ) R ( s )

1 + \K p +   + K d S I G p ( s )

I           s           )

• C.    DC-Servo Motor

The direct current (DC) servo motor is widely used in industry especially in high precision control such as robot arm and disk drive applications [25]. Regarding to control engineering context, analysis and design of the DC-servo motor control system require its accurate model parameters. Generally, such the parameters can be obtained by the blocked-rotor, no-load and retardation tests [26]. However, obtained parameters by these tests often inaccurate due to its uncertainty and error in testing process [26]. Another approach to obtain the model parameters is called the identification approach. Traditionally, model and parameter identification requires the knowledge of system input and output which can be obtained from the particular tests [27, 28]. The model parameters are then obtained by the regression analysis. By this approach, the obtained models are known as the black-box ones consisting of ARX, ARMAX, OE, and BJ, respectively [29]. By literatures, the conventional identification approach has been widely used to linear [30] and nonlinear system [31]. Although their closed-form formulation provide an advantage leading to fast computation, its major drawback is the restriction of the class of models to be difference equations and the like. Moreover, it is not possible to apply the method to identify models of other forms. To-date, metaheuristic optimization techniques have become potential candidates to various engineering applications. Among the    trajectory-based metaheuristic optimization techniques, the adaptive tabu search (ATS) is one of the most efficient methods. The ATS has been launched in 2004 [32, 33] as a modified version of the conventional tabu search for solving various engineering optimization problems especially in control synthesis and design problems [34, 35]. From our previous work [36, 37], the ATS-based model parameter identification of a DC-servo motor is presented method. The proposed identification approach can be considered as a class of metaheuristic optimization problems. Results obtained by the ATS will be compared with those obtained by the genetic algorithm (GA), one of the well-known and widely accepted population-based metaheuristic techniques.

• D.    DC-Servo Motor Model

The schematic diagram of armature-controlled DC-servo motor can be represented by Fig. 5 [38, 39], where Ra is an armature-winding resistance, La is an armaturewinding inductance, Rf is a field-winding resistance, Lf is a field-winding inductance, J is a moment of inertia, B is a viscous-friction coefficient, ea(t) is an applied armature voltage, ia(t) is an armature current, ef(t) is a field voltage, if(t) is a field current, eb(t) is a back emf (electromotive force) voltage, T(t) is a motor torque, 6(t) is an angular displacement and йХt) is an angular velocity (speed), respectively. The ea(t) is considered as the system input and йХt) stands for the system output. Referring to Fig. 5, the applied armature voltage ea(t), for the electrical part, can be formulated as expressed in Eq.(8), where Kb is back emf constant. For the rotational mechanical part, the motor torque T(t) is performed as stated in Eq.(9), where Kt is motor constant.

In practical, the DC-servo motor is usually driven by the power amplify (power electronic devices) which can be approximated by the power amplifier constant K A . Therefore, the math model of armature-controlled DC-servo motor speed control in term of the transfer function can be formulated by taking differential equations and Laplace transform as expressed in (10). The plant G_p(s) of the DC-servo motor can be identified via MATLAB and system identification toolbox. The second-order transfer function model obtained by this approach can be expressed in (11).

R a

L a

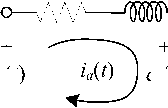
О ea(t) -

e b ( t )

B

6 ( t )

Lf Rf if(t) ef(t)

Fig.5. Schematic diagram of DC motor.

ea (t) = Raia (t) + La ^^ + eb (t), dt                          ^

= R a i a ⁽ t ) ⁺ L a ^a^ ^{+ K} b ® ⁽t ),   e b ⁽ t ) = K b ® ( t )

dtJ

T (t) = Kia (t) = Jd^^t) + B®( t)(9)

dt

^(s) =    _______KaK (10)

E a ⁽ S )   JL a S 2 + ( BL a + JR a ) S + ( BR a + K t K_b )

By substituting for the DC motor parameters in (10), The transfer function is:

G p ( s ) =

189.6565

0.0001486 s ² + 76.3867 s + 132.4162

• V.    Ats-Based Design of I-PD Controller

The ATS-based design of the I-PD controllers is illustrated in this section. Referring to Fig. 1, the AI

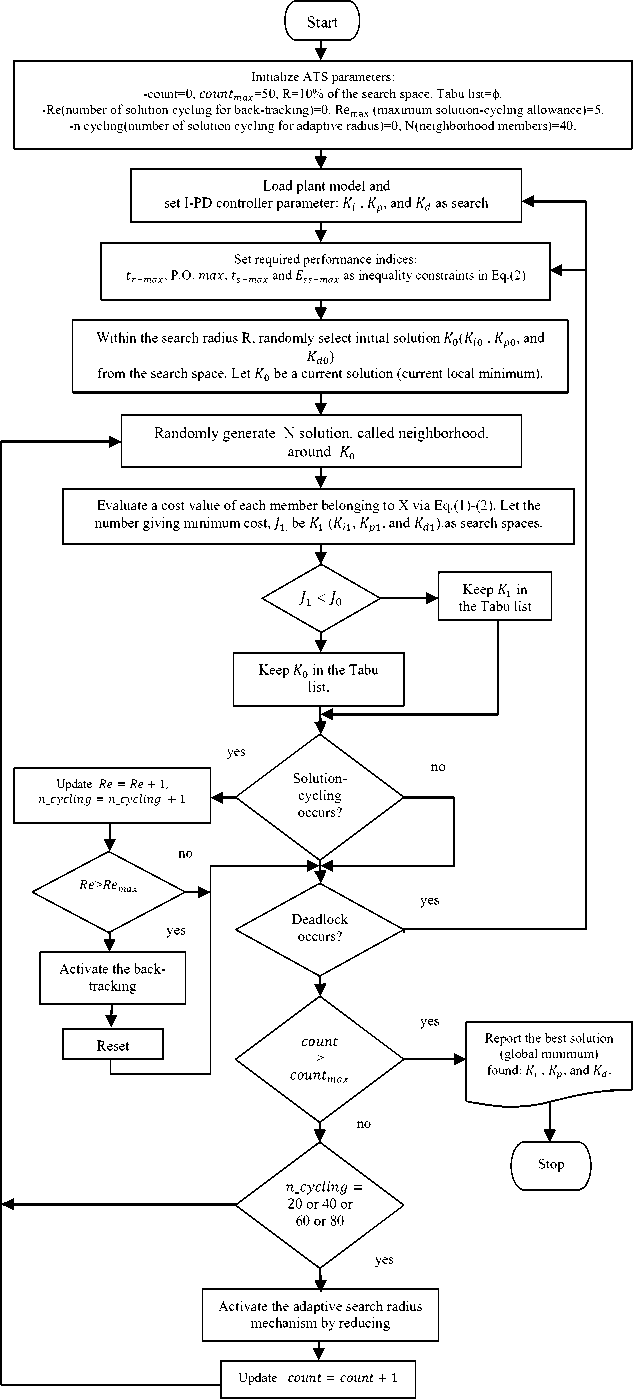
Fig.6. Diagram of the ATS’s implementation for designing I-PD controller tuning block utilizes the ATS method. The parameter tuning process is repeatedly performed to minimize the cost function J stated in (1)-(2) until the termination criterion is met. In this work, the maximum search round (          ) of the search process is the termination criterion. In each search round, 40 neighborhood members are randomly generated, and           is set as 50. Diagram of the ATS’s implementation for designing I-PD controller as shown in Fig. 6.

The diagram in Fig. 6 reveals the search process of the ATS for designing PID and I-PD controllers. In this work, the ATS was coded in MATLABTM for running on an Intel(R) Core (TM) i5-2450M CPU@ 2.5 GHz, 4 Gbytes RAM ,500 Gbytes HD. The flow diagram gives a clear view of the proposed method for the readers to follow. For more details of the back-tracking and the adaptive search radius mechanisms, the readers should consult the references [23, 24].

• VI.    Simulation and Experimental Results

• A.    Simulation Results

In this sub-section, after the search process stop, the optimal PID and I-PD parameters are successfully obtained as summarized in Table 1-3. The simulation results of DC Motor Speed Controlled system with I-PD controller designed by the ATS method in (1) shown in Fig. 7 will be confirmed by the experimental results as described in next sub-section.

Table 1. Results of two controllers test parameters

Controllers	Parameters
	K p	K i	K d
PID	9.976440	12.821038	0.000551
I-PD	3.031736	19.989464	0.006679

Table 2. Results of PID controller test parameters

System responses
t r (sec.)	t s (sec.)	M p (%)	E ss (%)	t reg (sec.)
0.1562	0.8530	15.654	0.00	2.1246

Table 3. Results of I-PD controller test parameters

System responses
t r (sec.)	t s (sec.)	M p (%)	E ss (%)	t reg (sec.)
0.2146	0.9140	11.228	0.00	1.2652

Referring to Table 1-3, as simulation results, it was found that the ATS can provide the optimal PID and I-PD parameters satisfying the constraints in (2). For the system responses in Fig. 7. By comparison, the controlled system with the I-PD provides significantly better responses with smaller overshoot and faster regulating time once compared to that with the parallel PID controller.

System responses obtained by the I-PD designed by the ATS will be compared with those obtained by basic parallel PID controller designed by the ATS. After the search process stopped, the optimal PID and I-PD parameters are successfully achieved as declared in Table 1-3. Their corresponding system responses are also reported in Table 1, where tr is rise time, ts is settling time and treg is regulating time. The step command and step disturbance responses of DC motor speed control system with PID and I-PD controllers are depicted in Fig.7.

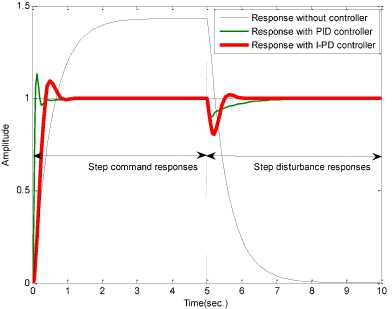
Fig.7. System responses without and with PID and I-PD designed by ATS.

• B.    Experimental Results

  The ATS is applied to design the PID and I-PD controllers for the DC motor speed control, the proportional and derivative kick, the PID controller produces much greater control signal than the I-PD does. This causes the serious problem once implemented. Therefore, the I-PD controller is more practical for real-world implementation. In this work the operating speed of 1260, 1400 , and 1540 rpm with no load and full load conditions. To confirm the simulation result, the experimentation of DC motor speed control system need to be done. The PID and I-PD controllers designed by the ATS are implemented by the TMS320F28335 DSP controller board [40, 41] shown in Fig. 8 as the real time embedded control system. The TMS320F28335 DSP controller board consist of a 32-bit CPU and a singleprecision 32-bit floating-point. The 150 MHz system clock is provided by an on-chip oscillator. The kit includes a peripheral explorer board and a control CARD with the TMS320F28335 MCU. The board includes many hardware-bas peripheral components for interacting with the various peripherals common to C2000 MCUs, such as the ADC, PWMs, eCAP, I2C, CAN, SPI, McBSP and TMS320F28335 DSP controller board is designed to interface with MATLAB/Simulink running on PC.

The DC motor speed control system is developed as the testing rig by using digital signal controller technology as shown in Fig. 9 for perform the experimental results. The electric load is applied to the load disturbance.

The first step, according to PID controller designed by the ATS can be implemented due to the high values of control gains. From Fig. 10, it was found at 1,260 rpm that the system response provides tr =420 ms, ts = 620 ms, Mp = 12.329 %, Ess = 0.00 ms, treg = 500 ms, Once upon a time comparable to the simulation results, the system output of experimental results gives slower response.

Fig.8. The TMS320F28335 DSP controller board.

The next step, according to PID controller designed by the ATS can be implemented due to the high values of control gains. From Fig. 11, it was found at 1,260 rpm that the system response provides t_r =420 ms, t_s = 620 ms, M_p = 12.329 %, E_ss = 0.00 ms, t_reg = 500 ms, Once upon a time comparable to the simulation results, the system output of experimental results gives slower response.

The last step, according to PID controller designed by the ATS can be implemented due to the high values of control gains. From Fig. 12, it was found at 1,260 rpm that the system response provides t r =420 ms, t s = 620 ms, M p = 12.329 %, E ss = 0.00 ms, t reg = 500 ms, Once upon a time comparable to the simulation results, the system output of experimental results gives slower response.

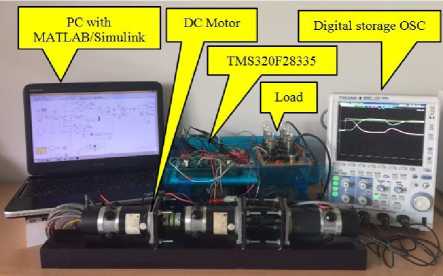
Fig.9. Testing rig of DC motor speed control system.

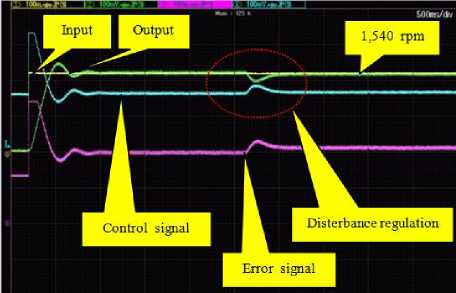
Fig.12. System responses of DC motor speed control system with PID controller.

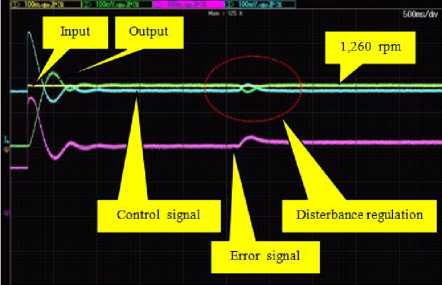
Fig.10. System responses of DC motor speed control system with PID controller.

The experimental result of DC motor speed control system with I-PD controller designed by the ATS is depicted in Fig.13-15. This proposed method is tested with the DC motor, 1260, 1400, 1540 rpm. The simulation results was compared in this case.

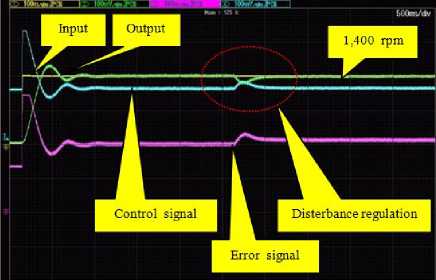
Fig.11. System responses of DC motor speed control system with PID controller.

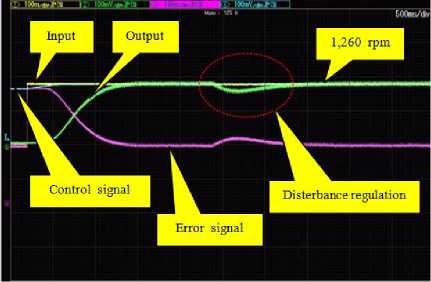
Fig.13. System responses of DC motor speed control system with I-PD controller.

The first step , according to I-PD controller designed by the ATS can be implemented due to the high values of control gains. From Fig. 13, it was found at 1,260 rpm that the system response provides t r =1,000 ms, t s = 1,100 ms, M p = 0.00 %, E ss = 0.00 ms, t reg = 520 ms, Once upon a time comparable to the simulation results, the system output of experimental results gives slower response.

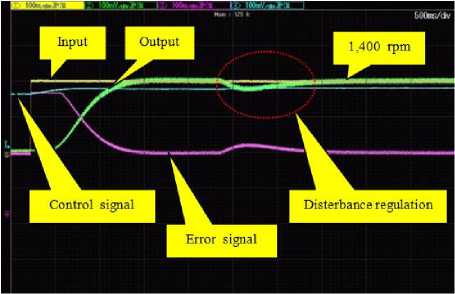
Fig.14. System responses of DC motor speed control system with I-PD controller.

The next step, according to I-PD controller designed by the ATS can be implemented due to the high values of control gains. From Fig. 14, it was found at 1,400 rpm that the system response provides t_r =1,000 ms, t_s = 1,100 ms, M p = 0.00 %, E ss = 0.00 ms, t reg = 600 ms, Once upon a time comparable to the simulation results, the system output of experimental results gives slower response.

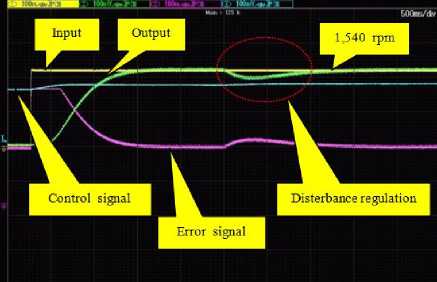
Fig.15. System responses of DC motor speed control system with I-PD controller.

The last step, according to I-PD controller designed by the ATS can be implemented due to the high values of control gains. From Fig. 15, it was found at 1,540 rpm that the system response provides t r =1,000 ms, t s = 1,100 ms, M p = 0.00 %, E ss = 0.00 ms, t reg = 1,000 ms, Once upon a time comparable to the simulation results, the system output of experimental results gives slower response.

• VII.    Conclusions

The optimal I-PD controller design for DC motor speed control system by the adaptive tabu search (ATS) has been proposed in this paper. The I-PD, one of the modified versions of the PID controller, has been proposed to avoid the proportional and derivative kick occurred during set-point change and to reduce undesirable overshoot. As the powerful metaheuristic optimization technique, the ATS has been conducted. The ATS could provide optimal PID and I-PD controllers for DC motor speed control system. By comparison, it can be concluded that the controlled system with I-PD provided better responses with smaller overshoot and faster regulating time as well as practical control signal.

Acknowledgment

The authors wish to thank the anonymous reviewers for their constructive comments that greatly contributed to improve the final version of the paper. Also, they wish to thank the Editors for their generous comments and support during the review process.