Design Intelligent System Compensator to Computed Torque Control of Spherical Motor

Multi-degree-of-freedom (DOF) actuators are finding wide use in a number of Industries. Currently, a significant number of the existing robotic actuators that can realize multi-DOF motion are constructed using gear and linkages to connect several single-DOF motors in series and/or parallel. Not only do such actuators tend to be large in size and mass, but they also have a decreased positioning accuracy due to mechanical deformation, friction and backlash of the gears and linkages. A number of these systems also exhibit singularities in their workspaces, which makes it virtually impossible to obtain uniform, high-speed, and high-precision motion. For high precession trajectory planning and control, it is necessary to replace the actuator system made up of several singleDOF motors connected in series and/or parallel with a single multi-DOF actuator. The need for such systems has motivated years of research in the development of unusual, yet high performance actuators that have the potential to realize multi-DOF motion in a single joint. One such actuator is the spherical motor. Compared to conventional robotic manipulators that offer the same motion capabilities, the spherical motor possesses several advantages. Not only can the motor combine 3-DOF motion in a single joint, it has a large range of motion with no singularities in its workspace. The spherical motor is much simpler and more compact in design than most multiple single-axis robotic manipulators. The motor is also relatively easy to manufacture. The spherical motor have potential contributions to a wide range of applications such as coordinate measuring, object tracking, material handling, automated assembling, welding, and laser cutting. All these applications require high precision motion and fast dynamic response, which the spherical motor is capable of delivering. Previous research efforts on the spherical motor have demonstrated most of these features. These, however, come with a number of challenges. The spherical motor exhibits coupled, nonlinear and very complex dynamics. The design and implementation of feedback controllers for the motor are complicated by these dynamics. The controller design is further complicated by the orientation-varying torque generated by the spherical motor. Some of these challenges have been the focus of previous and ongoing research [1-11].

In modern usage, the word of control has many meanings, this word is usually taken to mean regulate, direct or command. The word feedback plays a vital role in the advance engineering and science. The conceptual frame work in Feed-back theory has developed only since world war ІІ. In the twentieth century, there was a rapid growth in the application of feedback controllers in process industries. According to Ogata, to do the first significant work in three-term or PID controllers which Nicholas Minorsky worked on it by automatic controllers in 1922. In 1934, Stefen Black was invention of the feedback amplifiers to develop the negative feedback amplifier[12-28]. Negative feedback invited communications engineer Harold Black in 1928 and it occurs when the output is subtracted from the input. Automatic control has played an important role in advance science and engineering and its extreme importance in many industrial applications, i.e., aerospace, mechanical engineering and joint control. The first significant work in automatic control was James Watt’s centrifugal governor for the speed control in motor engine in eighteenth century[29-40]. There are several methods for controlling a spherical motor, which all of them follow two common goals, namely, hardware/software implementation and acceptable performance. However, the mechanical design of spherical motor is very important to select the best controller but in general two types schemes can be presented, namely, a joint space control schemes and an operation space control schemes[41-48]. Joint space and operational space control are closed loop controllers which they have been used to provide robustness and rejection of disturbance effect. The main target in joint space controller is to design a feedback controller which the actual motion ( qa(t) ) and desired motion ( qd (t) ) as closely as possible. This control problem is classified into two main groups. Firstly, transformation the desired motion Xd(t)  to joint  variable qd(t) by  inverse kinematics of  spherical motor[49-50]. This  control includes simple PD control, PID control, inverse dynamic control, Lyapunov-based control, and passivity based control. The main target in operational space controller is to design a feedback controller to allow the actual endeffector motion Xa (t) to track the desired endeffector motion Xd(t) . This control methodology requires a greater algorithmic complexity and the inverse kinematics used in the feedback control loop. Direct measurement of operational space variables are very expensive that caused to limitation used of this controller in spherical motor[51-55]. One of the simplest ways to analysis control of three DOF spherical motor are analyzed each joint separately such as SISO systems and design an independent joint controller for each joint. In this controller, inputs only depends on the velocity and displacement of the corresponding joint and the other parameters between joints such as coupling presented by disturbance input. Joint space controller has many advantages such as one type controllers design for all joints with the same formulation, low cost hardware, and simple structure. A nonlinear methodology is used for nonlinear uncertain systems (e.g., spherical motor) to have an acceptable performance. These controllers divided into six groups, namely, feedback linearization (computed-torque control), passivity-based control, sliding mode control (variable structure control), artificial intelligence control, lyapunov-based control and adaptive control[56-57]. The main targets in designing control systems are stability, good disturbance rejection to reach the best performance (robustness), and small tracking error[11-29]. Based on structure  and unstructured uncertainties strong mathematical tools used in new control methodologies to design nonlinear robust controller with an acceptable performance (e.g., minimum error, good trajectory, disturbance rejection). Computed Torque Controller (CTC) is one of the powerful nonlinear methodology, is used in nonlinear certain systems [30-57].This methodology is used in wide range areas such as in control access process, in aerospace applications, in robotic and in electrical motors, to solve some main challenging topics in control such as resistivity to the external disturbance and stability. Even though, this methodology is used in wide range areas but, pure CTC has two important drawbacks; structure and unstructured uncertainties.

In recent years, artificial intelligence theory has been used in sliding mode control systems. Neural network, fuzzy logic and neuro-fuzzy are synergically combined with nonlinear classical controller and used in nonlinear, time variant and uncertain plant (e.g., spherical motor). Fuzzy logic controller (FLC) is one of the most important applications of fuzzy logic theory. This controller can be used to control nonlinear, uncertain, and noisy systems. This method is free of some model techniques as in model-based controllers. As mentioned that fuzzy logic application is not only limited to the modelling of nonlinear systems [31-36] but also this method can help engineers to design a model-free controller. Control spherical motor using model-based controllers are based on manipulator dynamic model. These controllers often have many problems for modelling. Conventional controllers require accurate information of dynamic model of spherical motor, but most of time these models are MIMO, nonlinear and partly uncertain therefore calculate accurate dynamic model is complicated [32]. The main reasons to use fuzzy logic methodology are able to give approximate recommended solution for uncertain and also certain complicated systems to easy understanding and flexible. Fuzzy logic provides a method to design a model-free controller for nonlinear plant with a set of IF-THEN rules [32]. This paper contributes to the research effort of alternate methods for modeling the torque generated by the spherical motor used in the fuzzy sliding mode-type feedback controller design. The designed controller not only demonstrates the appealing features exhibited by the spherical motor, but also demonstrates some of the nice features of fuzzy sliding mode-type controllers as well. This paper is organized as follows; second part focuses on the modeling dynamic formulation based on Lagrange methodology, sliding mode controller to have a robust control, and design fuzzy logic compensator. Third part is focused on the methodology which can be used to reduce the error, increase the performance quality and increase the robustness and stability. Simulation result and discussion is illustrated in forth part which based on trajectory following and disturbance rejection. The last part focuses on the conclusion and compare between this method and the other ones.

• II.  Theorem

• • Dynamic and Kinematics Formulation of Spherical Motor

Dynamic modeling of spherical motors is used to describe the behavior of spherical motor such as linear or nonlinear dynamic behavior, design of model based controller such as pure sliding mode controller which design this controller is based on nonlinear dynamic equations, and for simulation. The dynamic modeling describes the relationship between motion, velocity, and accelerations to force/torque or current/voltage and also it can be used to describe the particular dynamic effects (e.g., inertia, coriolios, centrifugal, and the other parameters) to behavior of system[1-10]. Spherical motor has a nonlinear and uncertain dynamic parameters 3 degrees of freedom (DOF) motor.

The equation of a spherical motor governed by the following equation [1-10]:

н (q)

а

P

У

+ B(q)

ap ay PY

+ C(q)

a2P2

„2

■Й

Where τ is actuation torque, H (q) is a symmetric and positive define inertia matrix, B(q) is the matrix of coriolios torques, C(q) is the matrix of centrifugal torques. This is a decoupled system with simple second order linear differential dynamics. In other words, the component q influences, with a double integrator relationship, only the variable q / , independently of the motion of the other parts. Therefore, the angular acceleration is found as to be [1-11]:

q = H ~ ¹(q).{T-[B + C}}                   (2)

This technique is very attractive from a control point of view.

Study of spherical motor is classified into two main groups: kinematics and dynamics. Calculate the relationship between rigid bodies and final part without any forces is called Kinematics. Study of this part is pivotal to design with an acceptable performance controller, and in real situations and practical applications. As expected the study of kinematics is divided into two main parts: forward and inverse kinematics. Forward kinematics has been used to find the position and orientation of task frame when angles of joints are known. Inverse kinematics has been used to find possible joints variable (angles) when all position and orientation of task frame be active [1].

The following formulation is used to calculate Forward Kinematics:

• 5.    Setup joints coordinate frames.

• 6.    Determinea / , thata / , link twist, is the angle between and     about an .

• 7.    Determine d; and d , that ai , link length, is the distance between and     along .   , offset, is

• 8.    Fill up the D-H parameters table. The second step to compute Forward kinematics is finding the rotation matrix (R ° ). The rotation matrix from{Fj to {F/ _ -J is given by the following equation;

the distance between Xj __г and Xj along Z , axis.

R Г ¹ ■ и _KecV(_№                        (4)

Where U^i is given by the following equation [1-11];

fcos (Qt)  —sin(6i)  0

U_t (_{в t} ) = lstn( 0 )   с о s( 0 )   0

L o oi

and V/^.) is given by the following equation [1-11];

V (в) ■ l⁰   с о ^s( a)

1.0    sin (ct_t)

So (R ° ) is given by [8]

—s in( a] I COS (at) J

« n = (U1V1)(U 2 V 2)......... (Un V n )             (7)

The final step to compute the forward kinematics is calculate the transformation by the following formulation [3]

»T ■ 0 г. 1 Г. 2 r ■

№ 0

L 0 1

V (X,q ) = 0                                (3)

Where W (. )ERⁿ is a nonlinear vector function, X ■ [X₁,X₂, ......,X_;]^T is the vector of task space variables which generally task frame has three task space variables, three orientation, q ■ [q-^ q₂ > — ->q_n]^T is a vector of angles or displacement, and finally is the number of actuated joints. The Denavit-Hartenberg (D-H) convention is a method of drawing spherical motor free body diagrams. Denvit-Hartenberg (D-H) convention study is necessary to calculate forward kinematics in this motor.

A systematic Forward Kinematics solution is the main target of this part. The first step to compute Forward Kinematics (F.K) is finding the standard D-H parameters. The following steps show the systematic derivation of the standard D-H parameters.

• 1.    Locate the spherical motor

• 2.    Label joints

• 3.    Determine joint rotation ( 6 )

• 4.    Setup base coordinate frames.

Computed Torque Controller: Computed Torque Controller (CTC) is nonlinear controller, which is used in nonlinear certain and partly uncertain systems [30-53].This methodology is used in wide range areas such as in control access process, in aerospace applications, in robotic and in electrical motors, to solve some main challenging topics in control such as resistivity to the external disturbance and stability. Even though, this methodology is used in wide range areas but, pure computed torque controller dependence on the system dynamics that is the main challenge. The central idea of Computed torque controller (CTC) is feedback linearization method. It has assumed that the desired motion trajectory for the manipulator ( ) , as determined, by a path planner. Defines the tracking error as [23-37]:

e⁽t) ■ q ₄(t) — q_a(t)

Where e(t) is error of the plant, ( ) is desired input variable, that in our system is desired displacement, q_a (t) is actual displacement. If an alternative linear statespace equation in the form x ■ Ax + ВU can be defined as

и; mu         (io)

With U = —H^{- 1} (q).N(q,q)+H^-^.т and this is known as the Brunousky canonical form. By equation (8) and (9) the Brunousky canonical form can be written in terms of the state x = [e^T e^TY as [11-34]:

$ gh a-w(ii)

With

U = qd + H-4qHN(q.q)-T(12)

Then compute the required arm torques using inverse of equation (12), is;

T = H(qXqd-U) + N(q,q)(13)

This is a nonlinear feedback control law that guarantees tracking of desired trajectory. Selecting proportional-plus-derivative (PD) feedback for U(t) results in the PD-computed torque controller [8-10];

т = H(q)(q_d + K„e + K_pe) + ^(q, q)       (14)

Where N(_q, q") is nonlinear term of system dynamic;

^(q,q) = B(q) [qq] + C(q) [q]²                   (15)

According to the linear system theory, convergence of the tracking error to zero is guaranteed [6]. Where K_p and K_v are the controller gains.

Figure 1 shows the block diagram of nonlinear computed torque controller with application to spherical motor.

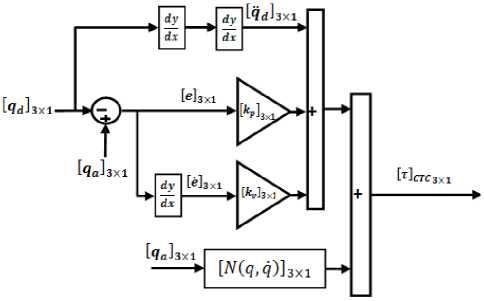
Fig. 1. Block diagram of computed torque Controller

Fuzzy Logic Theory: This section provides a review about foundation of fuzzy logic based on [32- 53]. Supposed that U is the universe of discourse and x is the element of U, therefore, a crisp set can be defined as a set which consists of different elements (x) will all or no membership in a set. A fuzzy set is a set that each element has a membership grade, therefore it can be written by the following definition;

Where an element of universe of discourse is x, p_A is the membership function (MF) of fuzzy set. The membership function ( ( )) of fuzzy set must have a value between zero and one. If the membership function p_A (x) value equal to zero or one, this set change to a crisp set but if it has a value between zero and one, it is a fuzzy set. Defining membership function for fuzzy sets has divided into two main groups; namely; numerical and functional method, which in numerical method each number has different degrees of membership function and functional method used standard functions in fuzzy sets. The membership function which is often used in practical applications includes triangular form, trapezoidal form, bell-shaped form, and Gaussian form.

Linguistic variable can open a wide area to use of fuzzy logic theory in many applications (e.g., control and system identification). In a natural artificial language all numbers replaced by words or sentences.

If — the it Rule statements are used to formulate the condition statements in fuzzy logic. A single fuzzy If — tilen rule can be written by

If x is A T hen у is В (17)

where A and В are the Linguistic values that can be defined by fuzzy set, the — of the part of “x is A ” is called the antecedent part and the tilen — part of the part of “y is В ” is called the Consequent or Conclusion part. The antecedent of a fuzzy if-then rule can have multiple parts, which the following rules shows the multiple antecedent rules:

if e is NВ an d e is ML then T is LL (18)

where e is error, e is change of error, MB is Negative Big, Mis is Medium Left, T is torque and LL is Large Left. If — tilen rules have three parts, namely, fuzzify inputs, apply fuzzy operator and apply implication method which in fuzzify inputs the fuzzy statements in the antecedent replaced by the degree of membership, apply fuzzy operator used when the antecedent has multiple parts and replaced by single number between 0 to 1, this part is a degree of support for the fuzzy rule, and apply implication method used in consequent of fuzzy rule to replaced by the degree of membership. The fuzzy inference engine offers a mechanism for transferring the rule base in fuzzy set which it is divided into two most important methods, namely, Mamdani method and Sugeno method. Mamdani method is one of the common fuzzy inference systems and he designed one of the first fuzzy controllers to control of system engine. Mamdani’s fuzzy inference system is divided into four major steps: fuzzification, rule evaluation, aggregation of the rule outputs and defuzzification. Michio Sugeno use a singleton as a membership function of the rule consequent part. The following definition shows the Mamdani and Sugeno fuzzy rule base

Mamdani F. R1: if   x is A and

у is В then z is C

Sugen о   F. R1: if    x is A nnd

у is В then     f (X,y) is C

transform fuzzy set to crisp set. Consequently defuzzification’s input is the aggregate output and the defuzzification’s output is a crisp number. Centre of gravity method ( C 0 G) and Centre of area method ( С О Л) are two most common defuzzification methods, which method used the following equation to calculate the defuzzification

C 0 G (Xk,y k)

When x and у have crisp values fuzzification calculates the membership degrees for antecedent part. Rule evaluation focuses on fuzzy operation (Л ND / 0R ) in the antecedent of the fuzzy rules. The aggregation is used to calculate the output fuzzy set and several methodologies can be used in fuzzy logic controller aggregation, namely, Max-Min aggregation, Sum-Min aggregation, Max-bounded product, Max-drastic product, Max-bounded sum, Max-algebraic sum and Min-max. Two most common methods that used in fuzzy logic controllers are Max-min aggregation and Sum-min aggregation. Max-min aggregation defined as below

T.I U ^Ti=v B(Xxk, У k, u ) Ы5= 1. hu(Xk, y k, U)

and     method used the following equation to calculate the defuzzification

C 0 A (Xk,y k)

Z i U i . ^(X k , y k , U i ) Z i / и. (Xk, y k, U)

В и (x k,yk,U) = n^.=1 F RdLx k, y k, U)

= m ax{ mi n [ ₌ i [/r _P q (X_k,y_k),/t_Pm(l/)]}

The Sum-min aggregation defined as below

в и (Xk,y k,U = r.ut^Fr i (x k, y k, u) = ^ min[= i [/rpq (Xk,yk), ДРт(Ю]

Where      (  ,   ) and      (  ,   ) illustrates the crisp value of defuzzification output, Ui E U is discrete element of an output of the fuzzy set, . (  ,   ,  ) is the fuzzy set membership function, and r is the number of fuzzy rules.

Based on foundation of fuzzy logic methodology; fuzzy logic controller has played important rule to design nonlinear controller for nonlinear and uncertain systems [53-66]. However the application area for fuzzy control is really wide, the basic form for all command types of controllers consists of;

• •    Input fuzzification (binary-to-fuzzy[B/F]conversion)

• •    Fuzzy rule base (knowledge base)

• •    Inference engine

where r is the number of fuzzy rules activated by x_k and and also ( , , ) is a fuzzy interpretation of ^ th rule. Defuzzification is the last

• Output          defuzzification          (fuzzy-to-

binary[F/B]conversion).

Figure 2 shows the part in fuzzy logic theory.

step in the fuzzy inference system which it is used to

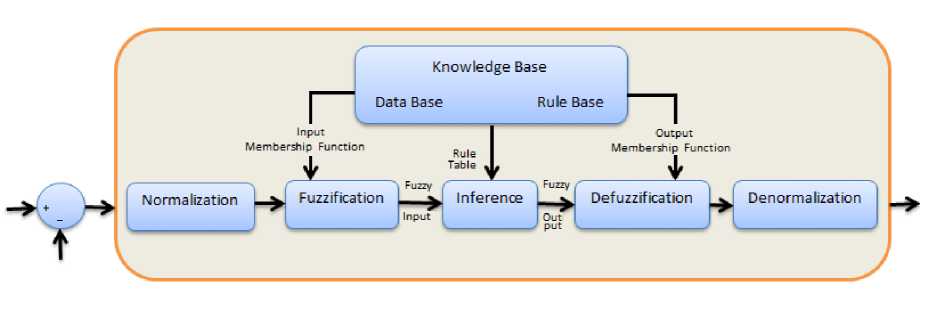
Fig. 2. Block diagram of Fuzzy Logic Control

III. Methodology

Computed torque controller (CTC) is one of the important nonlinear controllers in certain and partly uncertain dynamic system’s parameters. Conversely pure computed torque controller is a high-quality nonlinear controller; it has a problem dependence on system dynamics in presence of unknown conditions. To reduce

this challenge, this research is focused on applied parallel fuzzy logic theorem in pure computed torque controller as a compensator. This is suitable for real-time control applications when powerful processors, which can execute complex algorithms rapidly, are not accessible. The result of modified computed torque controller shows the application of power the controller in presence of partly uncertain conditions. In this research fuzzy logic

controller is used to estimate the dynamic parameters in computed torque controller which it has two inputs related to the error ( e , e) and one output ( U ^ _zzy) . All inputs and output are normalized between [-6 to 6]. Inputs have seven linguistic variables and all of linguistic variables have triangular membership function. The MAMDANI fuzzy inference system is used in this research. Therefore to model the dynamic of fuzzy controller 49 rule base is design based on MAMDANI fuzzy inference system. The center of gravity (COG) is used as a defuzzification.

The parallel fuzzy error-based compensator of computed torque controller’s output is written;

T   Ufls//V ■ TnT(24)

Based on fuzzy logic methodology f (x) = U zzzz= = Ei=i 9T ^to where 9T is adjustable parameter (gain updating factor) and ^(x) is defined by;

^E iM-^(x i)^x i

W"^iT(26)

Design an model-based parallel fuzzy compensate of equivalent part based on Mamdani’s fuzzy inference method has four steps, namely, fuzzification, fuzzy rule base and rule evaluation, aggregation of the rule output (fuzzy inference system) and defuzzification.

Fuzzification: the first step in fuzzification is determine inputs and outputs which, it has two inputs (e, e) and one output (V/Mzzy). The inputs are error (e) which measures the difference between desired and actual output, and the change of error (e) which measures the difference between desired and actual velocity and output is fuzzy equivalent torque. The second step is chosen an appropriate membership function for inputs and output which, to simplicity in implementation because it is a linear function with regard to acceptable performance triangular membership function is selected in this research. The third step is chosen the correct labels for each fuzzy set which, in this research namely as linguistic variable. Based on experience knowledge the linguistic variables for error (e) are; Negative Big (NB), Negative Medium (NM), Negative Small (NS), Zero (Z), Positive Small (PS), Positive Medium (PM), Positive Big (PB), and experience knowledge it is quantized into thirteen levels represented by: -6, -5, -0.4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6the linguistic variables for change of error (e) are; Fast Left (FL), Medium Left (ML), Slow Left (SL),Zero (Z), Slow Right (SR), Medium Right (MR), Fast Right (FR), and it is quantized in to thirteen levels represented by: -6, -5, -0.4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, and the linguistic variables to find the output are; Large Left (LL), Medium Left (ML), Small Left (SL), Zero (Z), Small Right (SR), Medium Right (MR), Large Right (LR) and it is quantized in to thirteen levels represented by: -6, -5, -0.4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6.

Fuzzy rule base and rule evaluation : the first step in rule base and evaluation is to provide a least structured method to derive the fuzzy rule base which, expert experience and control engineering knowledge is used because this method is the least structure of the other one and the researcher derivation the fuzzy rule base from the knowledge of system operate and/or the classical controller. Design the rule base of fuzzy inference system can play important role to design the best performance of parallel fuzzy plus computed torque controller, that to calculate the fuzzy rule base the researcher is used to heuristic method which, it is based on the behavior of the control of robot manipulator. The complete rule base for this controller is shown in Table 1. Rule evaluation focuses on operation in the antecedent of the fuzzy rules in fuzzy sliding mode controller. This part is used AND/OR fuzzy operation in antecedent part which AND operation is used.

Table 1. Fuzzy estimator rule base table applied to computed torque controller

D e ere a se t he о vers h oot     ё

	---------------------►         '								111 E e К
	\ё e\	FL	ML	SL	Z	SR	MR	FR
	NB	LL	LL	LL	ML	SL	SL	Z
	NM	LL	ML	ML	ML	SL	Z	SR
	NS	LL	ML	SL	SL	Z	SR	MR
	Z	LL	ML	SL	Z	SR	MR	LR	qj
	PS	ML	SL	Z	SR	SR	MR	LR	QJ
	PM	SL	Z	SR	MR	MR	MR	LR	QJ
	PB	Z	SR	SR	MR	LR	LR	LR	111 Q

Aggregation of the rule output (Fuzzy inference): based on fuzzy methodology, Max-Min aggregation is used in this work.

Defuzzification: The last step to design fuzzy inference in our parallel fuzzy compensator plus computed torque controller is defuzzification. This part is used to transform fuzzy set to crisp set, therefore the input for defuzzification is the aggregate output and the output of it is a crisp number. Based on fuzzy methodology Center of gravity method (COG) is used in this research.

T = H⁽q)(q_d + K_ye + K_pe) + N⁽q,q) + Z^ i 0^T<(x)                              ^{(   7}

Figure 3 shows the MAMDANI fuzzy model base computed torque controller with application to spherical motor.

Where a matrix of proportional coefficient is [K_p]_3xl , |K_y|_3xl is a matrix of derivative coefficient, [^ a l sxi , [^ $ ]₃ xi , [^]₃ xi are matrix of gain updating factor.

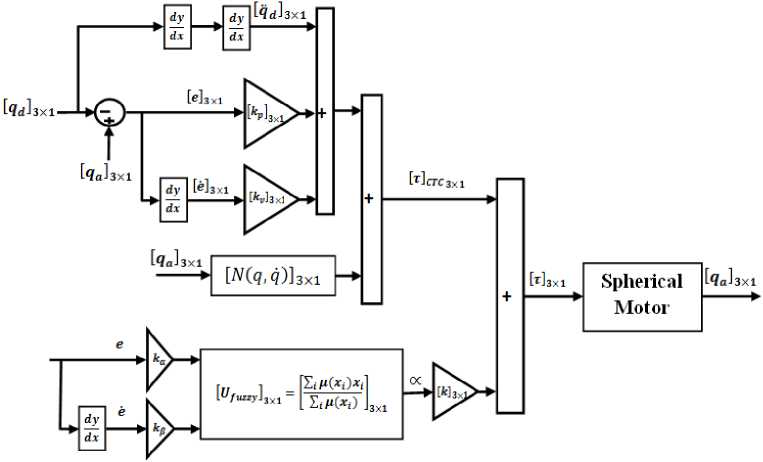
Fig. 3. Block diagram of Fuzzy Model Based Computed Torque Controller

• IV.    Results

Modified fuzzy compensator computed torque controller is implemented in MATLAB/SIMULINK environment. Tracking performance and disturbance rejection is compared for circle trajectory.

Tracking performances: From the simulation for first, second and third joints (spherical joints) without any disturbance, it was seen that proposed controller has a good trajectory performance, because this controller is adjusted and worked on certain environment. Figure 4 shows the tracking performance in certain system and without external disturbance this controller.

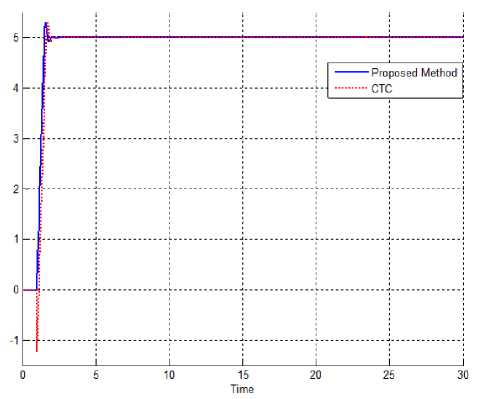
Fig. 4. Proposed Methodology and pure computed torque controller

According to above graph, pure computed torque controller have about 25% undershoot but proposed method can solve it based on methodology but all these two controllers have the same overshoot about 5%.

Disturbance rejection: Figure 5 shows the power disturbance elimination in pure compute torque controller and proposed method. The main targets in these controllers are disturbance rejection as well as the other responses. A band limited white noise with predefined of 40% the power of input signal is applied to controllers. It found fairly fluctuations in pure computed torque controller trajectory responses. Based on these two graphs, pure computed torque controllers have moderate fluctuations as well as 25% undershoot. These two important challenges can be solving based on intelligent nonlinear control design.

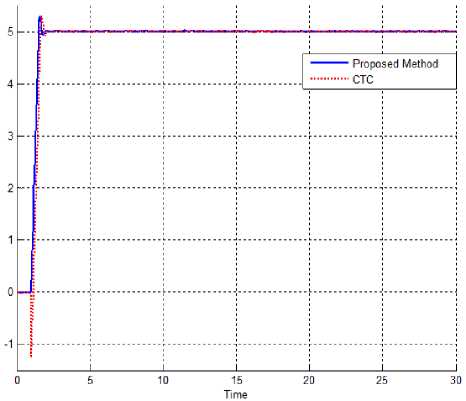
Fig. 5. computed torque controller and proposed method in presence of external disturbance

• V.    Conclusion

In this research, a multi-input-multi-output model base fuzzy computed torque control scheme is used to simultaneously control the speed rate of three ports torque to regulate the joint variable to desired levels. The control target is to have stability and robustness in presence of external disturbance and uncertainties. The first part of this controller is computed torque controller; this controller is one of the best nonlinear controllers in certain system. Fuzzy estimator methodology is applied to computed torque controller to obtain the best condition in presence on partly uncertainty and external disturbance. The ability to use proposed methodology on a MIMO case was significant. This methodology has acceptable performance in presence of uncertainty (e.g., overshoot=5%, rise time=0.4 second, steady state error = 1e-5, RMS error=1.45e-8 and undershoot=0%).

Acknowledgment

The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments. This work was supported by the SSP Institute of Advance Science and Technology Program of Iran under grant no. 2013-Persian Gulf-2A.