Design Novel Fuzzy Robust Feedback Linearization Control with Application to Robot Manipulator

Published Online April 2013 in MECS

Robot manipulator is collection of links that connect by joints, these joints can be revolute and prismatic that revolute joint has rotary motion around an axis and prismatic joint has linear motion around an axis. Each joint provides one or more degrees of freedom (DOF).

One of the most important challenges in the field of robot manipulator is control of it; because this system is multi input multi output (MIMO), nonlinear, time variant parameter and some dynamic parameters are uncertainty [1-2]. Presently, robot arms are used in different (unknown and/or unstructured) situation consequently caused to provide complicated systems, as a result strong mathematical theory applied to new control methodology to design nonlinear robust methodology to guarantee the security in industrial factory. Classical and non-classical methods are two main categories of nonlinear plant control, where the conventional (classical) control theory uses the classical method and the non-classical control theory (e.g., fuzzy logic, neural network, and neuro fuzzy) uses the artificial intelligence methods. However both of conventional and artificial intelligence theories have applied effectively in many areas, but these methods also have some limitations to have an acceptable secure performance in unknown environment [1-10].

The main targets in designing control systems are stability, good disturbance rejection to reach the best performance (robustness), and small tracking error[11-29]. Based on structure and unstructured uncertainties strong mathematical tools used in new control methodologies to design nonlinear robust controller with an acceptable performance (e.g., minimum error, good trajectory, disturbance rejection). Feedback linearization controller (FLC) is one of the powerful nonlinear methodology, is used in nonlinear certain systems [30-53].This methodology is used in wide range areas such as in control access process, in aerospace applications, in robotic and in internal combustion (IC) engines, to solve some main challenging topics in control such as resistivity to the external disturbance and stability. Even though, this methodology is used in wide range areas but, pure FLC has an important drawbacks beside uncertain system and also in presence of external disturbance.

Artificial intelligence theory is used to solve this problem. Neural network, fuzzy logic, and neuro-fuzzy are synergically combined with nonlinear classical controller and resolved the conventional controller against to uncertainty [30-41]. Fuzzy logic theory (FLM) can be used to resolve the model base challenge in nonlinear, uncertain, and noisy systems. Conventional controllers often have many problems for modelling nonlinear dynamic system’s parameter. Conventional controllers require accurate information of dynamic model of robot arms. When the system model is unknown or when it is known but complicated, it is difficult or impossible to use conventional mathematics to process this model[32]. The main reasons to use fuzzy logic technology are able to give approximate recommended solution for unclear and complicated systems to easy understanding and flexible. Fuzzy logic provides a method which is able to model a controller for nonlinear plant with a set of IF-THEN rules, or it can identify the control actions and describe them by using fuzzy rules [32].

In various dynamic parameters systems to have stability and robustness, training on-line control methodology is used. Mathematical switching sliding mode methodology (MSM) is a significant nonlinear controller under condition of partly uncertain dynamic parameters of system. This method is used to control of highly nonlinear systems especially for robot manipulators, because this theory is a robust and stable. Switching sliding method is used to increase the stability and robustness based on LYAPUNOV base methodology. Conventional feedback linearization controller, fuzzy feedback linearization controller and switching sliding fuzzy feedback linearization controller have difficulty in handling unstructured model uncertainties. It is possible to solve this problem by proposed methodology and adaption law which this method can helps improve the system’s tracking performance by online tuning method. Mathematical error base methodology used to limitation tuning controller’s coefficient.

This paper is organized as follows; second part focuses on the modeling dynamic formulation based on Lagrange methodology, introducing to feedback linearization controller (computed torque controller), fuzzy logic methodology and sliding mode controller to have a robust control. Third part is focused on the methodology which can be used to reduce the error, increase the performance quality and increase the robustness and stability. Simulation result and discussion is illustrated in forth part which based on trajectory following and disturbance rejection. The last part focuses on the conclusion and compare between this method and the other one’s.

• II.    Theory2.1    Robot Manipulator’s Dynamic:

The equation of an n-DOF robot manipulator governed by the following equation [1, 4, 15-29, 41-53]:

M ⁽q)q+N⁽q,q'⁾ = T                       (1)

Where τ is actuation torque, M (q) is a symmetric and positive define inertia matrix, N(q,q^ is the vector of nonlinearity term. This robot manipulator dynamic equation can also be written in a following form [1-29]:

т = M(q)q + S(q)[q q] + C(q)[q]² + G(q)     (2)

Where B(q) is the matrix of coriolios torques, C(q) is the matrix of centrifugal torques, and G(q) is the vector of gravity force. The dynamic terms in equation (2) are only manipulator position. This is a decoupled system with simple second order linear differential dynamics. In other words, the component q influences, with a double integrator relationship, only the joint variable q , , independently of the motion of the other joints.

Therefore, the angular acceleration is found as to be [3, 41-53]:

q = M^-1(q). {т — N(q, q)}                      (3)

This technique is very attractive from a control point of view.

• (4)    and (5) the Brunousky canonical form can be written in terms of the state x = [е^г e^r]^r as [1]:

• 2.2    Feedback Linearization Method:

£ch ii-iei+[?i"             (6)

With

U = q_d+M^-1(q).{N(q.q)-f}         (7)

Feedback linearization method (FLC) is a powerful nonlinear controller which it widely used in control of robot manipulator. It is based on feedback linearization and computes the required arm torques using the nonlinear feedback control law. This controller works very well when all dynamic and physical parameters are known but when the robot manipulator has variation in dynamic parameters, in this situation the controller has no acceptable trajectory performance[14]. In practice, most of physical systems (e.g., robot manipulators) parameters are unknown or time variant, therefore, feedback linearization like controller used to compensate dynamic equation of robot manipulator[1, 6]. Research on FLC is significantly growing on robot manipulator application which has been reported in [1, 6, 15-16]. Vivas and Mosquera [8]have proposed a predictive functional controller and compare to FLC for tracking response in uncertain environment. However both controllers have been used in feedback linearization, but predictive strategy gives better result as a performance. A FLC with non parametric regression models have been presented for a robot arm[9]. This controller also has been problem in uncertain dynamic models. Based on [1, 6]and [8-9] FLC is a significant nonlinear controller to certain systems which it is based on feedback linearization and computes the required arm torques using the nonlinear feedback control law. When all dynamic and physical parameters are known, FLC works fantastically; practically a large amount of systems have uncertainties, therefore feedback linearization like controller is the best case to solve this challenge.

The central idea of FLC is feedback linearization so, originally this algorithm is called feedback linearization controller. It has assumed that the desired motion trajectory for the manipulator q_d(t) , as determined, by a path planner. Based on tracking error definition;

e tt) = d att) - q _att)                            (4)

Where e(t) is error of the plant, q_d(t) is desired input variable, that in our system is desired displacement, q _a(ts is actual displacement. If an alternative linear state-space equation in the form x = Ax + BU can be defined as

• *=G 0b+[0Ju                    (5)

With U = -M^-1 (q). N(q, q) + M^-1 (q). т and this is known as the Brunousky canonical form. By equation

Then compute the required arm torques using inverse of equation (7), is;

т = M(q)(q d — U) + N(q, q)                  (8)

This is a nonlinear feedback control law that guarantees tracking of desired trajectory. Selecting proportional-plus-derivative (PD) feedback for U(t) results in the PD-FLC [6];

т = M ⁽ q)(q_d + K_ve + K_pe) + N⁽q, q)         (9)

and the resulting linear error dynamics are

(q_d+ к_Ре + к_ре) = 0                       (10)

According to the linear system theory, convergence of the tracking error to zero is guaranteed [6]. Where K_p and K_p are the controller gains.

• 2.3    Fuzzy Inference Engine:

The firs type of fuzzy systems is given by

м fto = 2

l=1

E^lE^l(x) = 9^TE(x)

Where

9 = (9¹..... 9^)^T,E(x) =

(E¹(x), ..., Е^м(x))^T, and E^l(x) =

M,Z ⁽ r_;)

:ПГ=1^^Z?=1(ПГ=1^л/(xi)).      91.....9м are adjustable parameters in (11) . ^Ai(x1), -■, ^A^(xn) are given membership functions whose parameters will not change over time.

The second type of fuzzy systems is given by

E ?= , 9^lln "= _lexp(-(^x^-3) )] яф = ехр ^{(   (} .' '' 'I

Where , are all adjustable parameters. From the universal approximation theorem, we know that we can find a fuzzy system to estimate any continuous function. For the first type of fuzzy systems, we can only adjust 9^l in (12). We define f (x|9) as the approximator of the real function ( ) .

f^(X|в)= 0T E(X)

We define 9 ^∗ as the values for the minimum error:

9∗ =argmin[suр|f ^(x|9)- g(X)|]

∈£1 Lx∈ U-I

Where

	Г 8i , 9i ,	, е^д
⊖ T = ( 9i ,…,  ) T =	9^ , el ,	, 9? ⎥
	⎣ 0L.02 .. ,           ,	AM …,

Where /2 is a constraint set for в . For specific X , sup_{x ∈} U | f ^ ₍ X | 0 ^∗)- f ( X )| is the minimum approximation error we can get.

We used the first type of fuzzy systems (11) to estimate the nonlinear system (9) the fuzzy formulation can be write as below;

f ( X | 0 )= 0^TE ( X )

∑ ^i9^L [ g_Ai ( x )] (15) =_∑?=i [ g_Ai ( X )]

Where 9¹ ,…, 9^ are adjusted by an adaptation law. The adaptation law is designed to minimize the parameter errors of 9 - 9 .

£( x )=(E¹ ( X ),…, E^M ( X )) I , E¹( X )=∏ ^B_A\ ( Xi )/ ∑ "1(∏ ^=W_t ( Xi )) , and g_A\ ( Xi ) is defined in (15). To reduce the number of fuzzy rules, we divide the fuzzy system in to three parts:

F¹ ( q , ̇)= ⊖^1T £ ( q , ̇)

= 0 0fs ( q , ̇) ,…, 9_m £ ( q , ̇) 1       ⁽²²⁾

F² ( q , ̈ )= ⊖^2? £ ( q , ̈ )

= 0 0ffi ( q , ̈ ) ,…, 9_m £ ( q , ̈ ) 1

• 2.4    Switching Linear Sliding Methodology:

Based on switching linear sliding method discussion, the control law for a multi degrees of freedom robot manipulator is written as [18-24, 63-74]:

и ^{=          +} Udis

Where, the model-based component UNonlinear is compensated the nominal dynamics of systems. A simple solution to get the switching linear sliding method condition when the dynamic parameters have uncertainty is the switching control law:

Udis =  ( ⃗, t) ∙sgn(S)

where the switching function Sgn ( s ) is defined as

1s>0

sgn(s)={-1

and the К ( ⃗ ⃗, t ) is the positive constant.

• III.    Methodology

The general SISO if-then rules are given by

Rl :             , x2 is A2,…,xn is ALn ,tℎen yjs ВД,…,Ут is Um

Where I =1,2,…, M are fuzzy if-then rules; = ( %1 ,…, X_n ) T and У =( У1 ,…, Уп ) T are the input and output vectors of the fuzzy system. The SISO fuzzy system is define as

f ( X )= ⊖ ^T E ( X ) (20)

F³ ( q , ̈)= ⊖ ^3T E ( q , ̈)

= 0 0^3TE ( q , ̇) ,…, 9_m £ ( q , ̈) 1          (24)

The control security input is given by

T =        ̈  + В ( q ) ̇ ̇+ c ( q ) ̇²+

g ( q )+ F¹ ( q , ̇)+ F² ( q , ̈ )+ F³ ( q , ̈)-     (25)

K_pe - Kyt ̇

Where M , В(q) ̇ ̇, C(q) ̇'2 ,g(q)   are the estimations of M(q).

Based on feedback linearization formulation (9) and switching sliding methodology (17);

^New =  ( q )( ̈ d + Kyt ̇+ K_pe )

And ^switch is obtained by

Uswitch =K(⃗х⃗, t) ∙sgn(SNew) =K(⃗х⃗, t)∙ sgn (M(q)(q̈d+K е̇+Kpе))

The Lyapunov function in this design is defined as

M

V= STMS+2∑ y~-^T․ Ф1(28)

where Vsj is a positive coefficient, Ф=  ∗-в,в∗ is minimum error and 9 is adjustable parameter. Since ̇ -2 is skew-symetric matrix;

STMṠ+1STK̇ 'S =   (Mi̇+vs)

If the dynamic formulation of robot manipulator defined by

Т=   ( q ) ̈+ v ( q , ̇) ̇ + g ( q )

Based on Ф = ∗ - e → e = ∗ - Ф

the controller formulation is defined by

T = ̂ ̈ + ̂ ̇ + ^̂ - AS - К

V̇ =

∑J=1 [Sj (Δf j - θ∗ T ζ(Sj)+фтζ(Sj)]-STλS+

∑ r^ γ-Фт ․ ̇

γ

According to (29) and (30)

M ( q ) ̈+ v ( q , ̇) ̇ + G ( q )= ^̂ ̈ + ^̂ ̇ +

̂-  -

Since ̇  = ̇ - and ̈  = ̈ - ^̇

^̇ +( V + A ) s =∆ f - к

M ̇= M - к - vs - AS

The derivation of V is defined

„          1 „ .                          .

̇= S^TM^ ^̇ + ¹ s^т^ ^̇ ’S +∑ ¹ -ф^т ․q ^̇

2              Tsi j=lrsJ

M

∑ —ф^т ․ ^̇

7=1Ysj

Based on (32) and (33)

̇ =∑[Sj (Mi-(e ∗) 4( Sj)]-STAS l=i ∑   ■             _

— Фу [ Ysj ^․ Sj ^․ ^j ( Sj )+ ^̇ >j ])

j=i Ysj where ̇ 'j =        ( Sj ) is adaption law, ∅̇ , =- ̇ =

^- YsjSj^j ⁽ Sj ₎

̇ is considered by

V̇ =ST( Δ f-K

∑J^l γL*T․ ̇ γ where

∑ 7=^4 ( X )

M

-VS- λ S+VS)+

∆ f =[ M ( q ) ̈+ v ( q , ̇) ̇ + g ( q )]-

̇ =∑[ Sj ( Mi - ^Ki )]- S^TAS + /=1

suppose Лу is defined as follows

К = ^∑ м ^[ ЦА ⁽ Sj )] ₌    ( _s )

Kj =_∑Г.,[ Цд ( Sj )] ⁼ 6,^ ⁽ S, )

M

^∑ Ysj^ ․ ̇

/=1 1

( ^Wh ) ^e = ^re [  ( ),   ( ),   ( ),…․․,   ( )]

( 5 )= "⁽*⁾; ⁽5⁾

( )=_∑ tn ( A ) ' ( Sj ₎

where Ц ₍ xi ₎ is membership function.

The fuzzy system is defined as

∑

9^Tf ( X )= Ф ( e , t ̇)

1=1

where e =(s¹, e², e³ ,……․, 9^м ) is adjustable parameter in (36)

according to 33, 34 and 36;

̇=∑ 7-i [ Sj ( Δ fi ^- 9^T^ ( Sj )]- S^TAS +

^∑ 7=1^Ф^{Т ․} <1 ̇

Ysj

̇ =∑[Sj ∆ fj -.(e ∗) T^j ( Sj)/]-STAS(41)

i=i

The minimum error is defined by

=∆fj-.(e ∗) Tfj ( Sj )/

Therefore ̇ is computed as

̇ =∑[Sj emj]-STAS(43)

i=i

≤∑ T=i | Sj ||   |- S^TAS

=∑| Sj ||   |- AjSj²

i=i

=∑| Sj |(|   |- AjSj )                     (44)

i=i

For continuous function 9 ( x ) , and suppose £ >0 it is defined the fuzzy logic system in form of

SuPx ∈ и | f ( X )- g ( X )|< 6                   (45)

the minimum approximation error (   ) is very small.

if ''-j =      ℎ at   a | Sj |>     ( Sj ≠

0)    t ℎ en  ̇<0 for ( Sj ≠0)

This method has two main controller’s coefficients, K_p and K_v . To tune and optimize these parameters mathematical formulation is used

U ^{=       +} Gswitch

U=Ufuzzy+Uswitch = K(⃗х⃗, t) ∙ sgn .M(q)(q̈d+Kv—new е̇ + Kp-newе)/ +

∑1=1 θ	*∏'Ll exp ( ( δ α 5 ))+
∑1=1*	∏ [L^xp( ( δ , α 1))+

Kp—new =   × Kc                          (49)

^V—new =   × Kc                          (50)

( t ̇( t )- t ̇( t -1))

• IV.    Results and Discussion

  Trajectory following: Based on simulation results the Steady State and RMS error in proposed method (Steady State error =1e-6 and RMS error=1.2e-6) are fairly lower than FCTC’s (Steady State error ≅ -3e -5 and RMS error=-1․ 34e -5) and CTC’s (Steady State error ≅ - 0․ 001 and RMS error=0.00652) .

TZ _       ⁽ r_v - ^v—min ⁾

=   -              +                   ⁽⁵¹⁾

1+| |

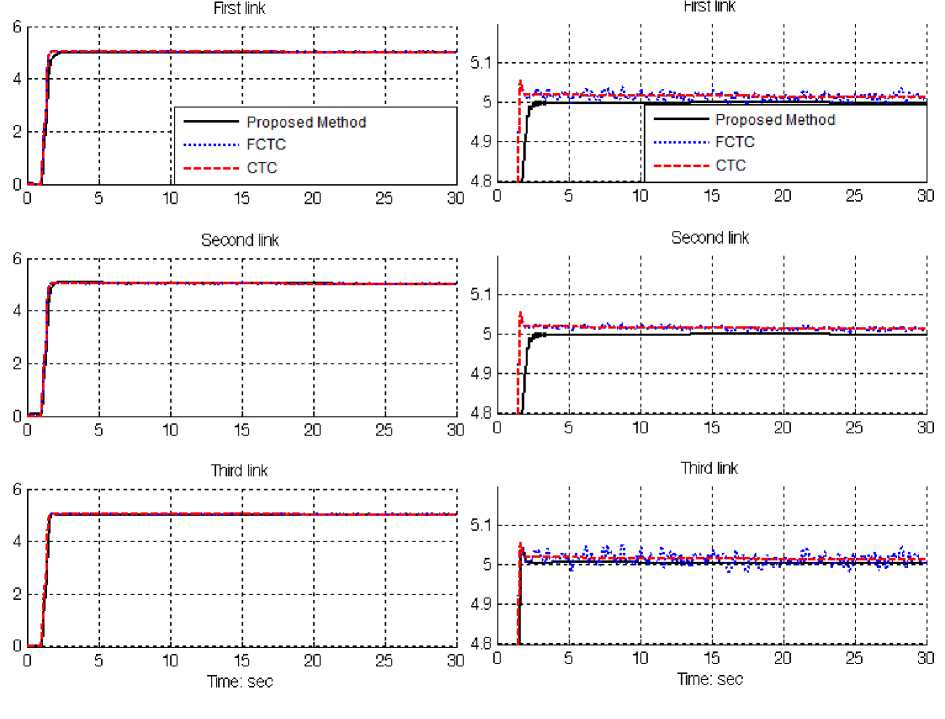
Fig. 1: Trajectory following (proposed method, FCTC, CTC)

Based on Figure 1, step trajectory performance is used for comparisons of above controllers in certain systems. In this state proposed method has better trajectory performance but FCTC has oscillation.

Disturbance rejection: Figure 2 illustrates the CTC, FCTC and proposed method. The disturbance rejection is used to test the robustness comparisons of these three controllers for step trajectory. A band limited white noise with predefined of 40% the power of input signal is applied to the step trajectory. It found fairly fluctuations in trajectory responses. Based on Figure 2; by comparing step response trajectory with 40% disturbance of relative to the input signal amplitude in CTC, FCTC and proposed method, proposed method’s overshoot about (1%) is lower than FCTC’s (8%)and CTC’s (9.1%). Besides the Steady State and RMS error in proposed method (Steady State error =1.6e-6 and RMS error=1.9e-6) are fairly lower than CTC’s

(Steady State error ≅ о․ 003 and RMS error= о․ 0048 ) and FCTC’s (Steady State error ≅-О․1 and RMS error=0. 652). Based on Figure 2, proposed method has fairly oscillation in trajectory response with regard to 40% of the input signal disturbance but this controller is more robust.

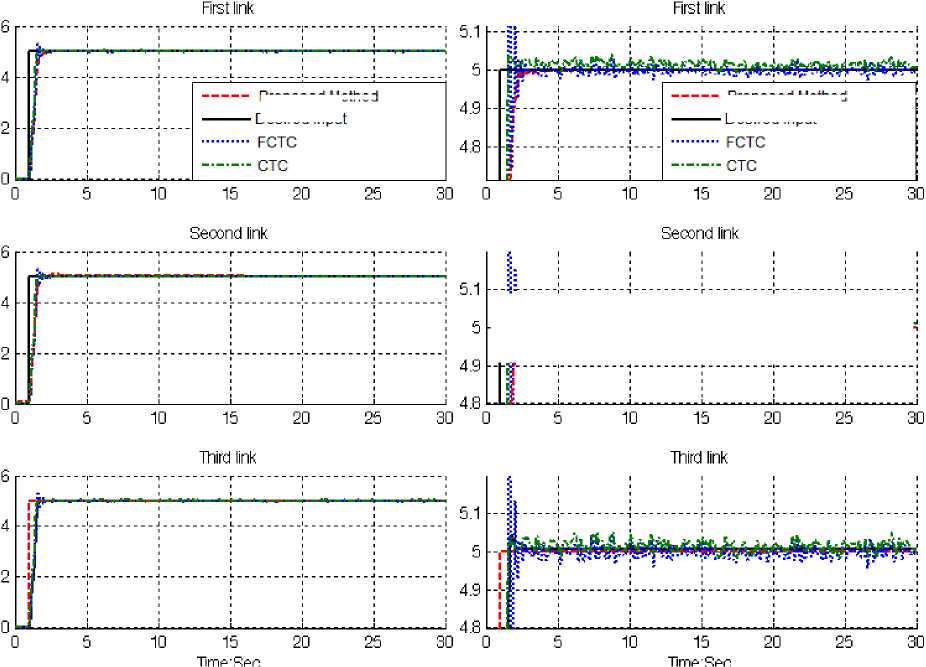
Proposed Method

Desired Input

Fig. 2: Disturbance rejection (proposed method, FCTC, CTC)

Proposed Method

Desired Input

	SC*-»k

Disturbance rejection: steady state error is an important parameter to test the system’s performance. In system with 40% disturbance the comparison between steady state error is; (Steady State error =1.6e-6 and RMS error=1.9e-6) are fairly lower than CTC’s (Steady State error ≅ 0․ 003 and RMS error= 0․ 0048 ) and FCTC’s (Steady State error ≅-0․1 and RMS error=0. 652) .

• V.    Conclusion

Refer to this research, a mathematical tuning fuzzy switching sliding feedback linearization method with application to robot manipulator has proposed. Stability and robustness are two more important challenges to design high performance nonlinear controller in the presence of uncertainties and external disturbances. Regarding to the positive points in feedback linearization methodology, fuzzy inference system and sliding switching methodology, stability and robustness are resolve based on eliminate the nonlinear dynamic equations and LYAPUNOV based stability formulation. To have a wide band limitation robust against to structure and unstructured uncertainty mathematical performance based tuning is applied to proposed method. Regarding to this methodology the values of error reduce to 1.6 micro which in industry this value is equal to zero.

Acknowledgment

The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments. This work was supported by the SSP Research and Development Corporation Program of Iran under grant no. 2012-Persian Gulf-3C.