Design of generalized weighted Laplacian based quality assessment for software reliability growth models
Автор: Chandra MouliVenkata Srinivas Akana, C. Divakar, Ch. Satyanarayana
Журнал: International Journal of Information Technology and Computer Science @ijitcs
Статья в выпуске: 5 Vol. 10, 2018 года.
Бесплатный доступ
The reliability of a software depends on the quality. So, the software growth models require efficient quality assessment procedure. It can be estimated by various parameters. The current paper proposes a novel approach for assessment of quality based on the Generalized Weighted Laplacian (GWL) method. The proposed method evaluates various parameters for detection and removal time. The Mean Value Function (MVF) is then calculated and the quality of the software is estimated, based on the detection of failures. The proposed method is evaluated on process CMMI level 5 project data and the experimental results shows the efficiency of the proposed method.
Quality Assessment, Software Reliability Growth Models, residual fault, fault detection rate and NHPP
Короткий адрес: https://sciup.org/15016262
IDR: 15016262 | DOI: 10.5815/ijitcs.2018.05.05
Текст научной статьи Design of generalized weighted Laplacian based quality assessment for software reliability growth models
Published Online May 2018 in MECS
The estimation of Software quality is made using Product, Process and Project (PPP) metrics. They are deeply connected with the product and process. These are further classified as in-process and end product quality metrics [1]. Software reliability models are mainly categorized into two types: Defect density models and software reliability growth models (SRGM). Defect density models analyze software defects using code characteristics viz., lines of code, external references, nesting of loops etc. SRGMs use statistics to associate defect detection with known functions such as exponential functions.
Nowadays, organizations rely on a variety of SRGMs to accurately analyze the software’s reliability [2] and to improve the process of software testing. In spite of their success the SRGMs have their own set of problems. It is found that the fault detection is not stable [2] in S-shaped models. The logistic function is found to be efficient for incorporating into SRGM. The current SRGMs are evaluated based on the derived general requirements [3].
Homogeneous Poisson process [4][5] used for SRGM development considers both change-point and testing effort. Here, the fault detection rate is found to vary, depending on various parameters. The Non Homogeneous Poisson process (NHPP) [6] with the combination of error generation and imperfect debugging is suitable for SRGM. These are intended for the fault observation and removal processes. The Log-Logistic curve [7] showing the testing effort is explained using time-dependent behavior. Discrete calculus and stochastic differential equations [8] are used for development of the SRGM.
-
II. Related Work
The Poisson model [9] decreases the fault rate in geometric progression. Exponential, normal, gamma and Weibull functions are also used to design the SRGM. The SRGMS are abstractly unsuitable [10] for various proprietary data sets cross study comparisons and leads to an inadequate usage of statistical testing results. For NHPP, the Exponential Weibull testing effort function (TEF) [11] is used for designing the inflection S-shaped SRGMs. It is found to be flexible with imperfect debugging. For Noisy input, the analysis of sensitivity [12] is required to measure the conclusion stability in terms of noise levels concerned. The genetic programming based on symbolic regression [13] is found to be efficient for SRGM design. A hierarchical quality model [14] based SRGM is automatically calculates the metric values and their correlation with various quality profiles. The distance based approach (DBA) [15] based SRGM is evaluated for selecting the optimal parameters and yields the ranking. It identifies the importance of criteria for the application.
The Japanese software development system utilizes the Gompertz curve [16] for residual faults estimation. In SRGM, multiple change points are crucial for detection of environment changes [17]. These are known for efficiently handling both the imperfect and ideal debugging conditions. In SRGM, application of Queuing modes is used for describing the fault detection rate and correction procedure. For this, the extension of infinite server queuing models [18][19] is used based on multiple change points. The Component Based Software Development (CBSD) [20] is considered as building blocks for SRGM. The CBSD primarily focuses on selection of appropriate user requirements. Some of the soft errors can be minimized by using minimum redundancy concept of critical data [21]. In [22] Anjum et.al, presented a ranking based weighted criteria for reliability assessment where the failure data sets are ranked accordingly.
The existing SRGMs have failed to take care of faulty debugging, and hence this paper proposes a novel SRGM which considers both the residual faults and learning ability. This paper is divided into five sections. The section-1 discusses about the introduction, section II discusses about the related work, the section III discusses about the methodology, section IV discusses about the results and discussion and conclusions in section V.
-
III. Methodology
The present paper proposes a novel approach for quality assessment for software growth model. The design of the proposed methodology is discussed in section A and the estimation of performance measures is discussed in section B
-
A. Design
The methodology used is illustrated in Fig.1 below.
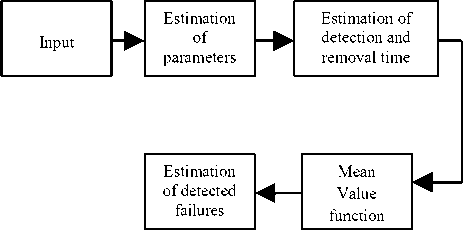
Fig.1. Block diagram of the Proposed Method.
The probabilistic model based software development process requires a Reliability Analysis. For this, the following hypothesis is considered:
Let H 0 : HPP and H 1 : NHPP
Here, H0refers to null hypothesis and
H1is the alternative hypothesis.
The equation for the Laplace trend derivation is:
U = L 6 ) ' (1)
E ( - L ( 6 0 ) ) "
Where,#0is a constituent of vector# with a value that removes the time-dependency of the intensity function λ(t;θ).
Let’s assume an error probability:
α=P{rejectH 0 | H 0 is true
The Laplace trend is expressed as:
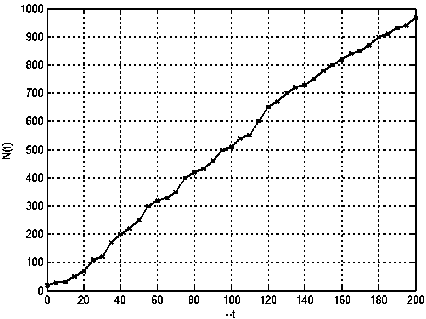
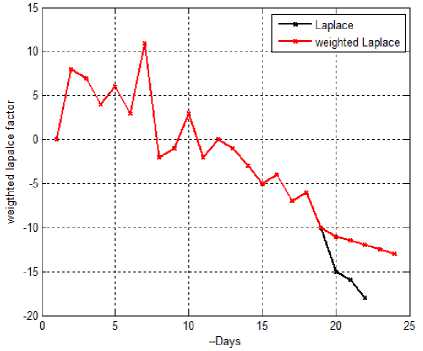
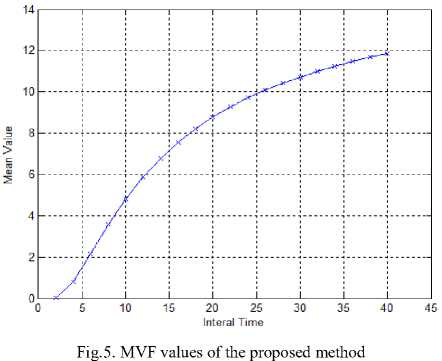
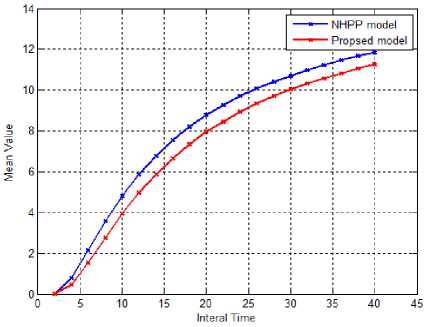
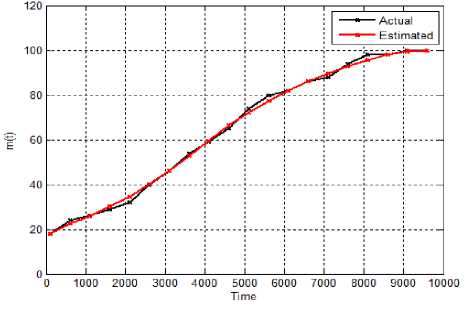
U U>Zα Reliability deterioration -Zαα Stable reliability Where, Zα lies in the upper α percentage in the standard normal distribution [23]. If U>Zα or U<-Zα, H0 can be ignored; or accept H0if -Zα≤U≤Zα. Software reliability test serves to identify the failure patterns that exhibit substantial changes over a period of time. If the event occurrences area NHPP representing a function of log-linear failure intensity A(t) = exp (a + pt), the null hypothesis for Laplace test can be expressed as: U (k ) = k-1 v'k ) i 2 ^ i=1 i I к2— 1 k n 12 Z-u=1 i The weighted approach of the proposed technique is based on the weight attribute. Let roe [0,1] be the weighted attribute indicating the amount of software reliability growth at time [tl,tl+tw]. Then the weighted failure intensity function A (t) is: Aw (t) = A(t) +w^(t) + (1 —w)^(tl ) (3) Where, λ(t)refers to the failure intensity function. If w=1,λw changes to λ(t). If w=0,λw is constant. Moreover, for ωε [0,1] λw carries a lighter tail than λ(t)in the period [tl,tl+tw]. Therefore, the weighted anisotropic Laplace test statistics is given by the expression [24]: Aw ( к) = A (к ) + WA (k ) + (1 —W) A (tl) (4) B. Estimation of Performance Measures The proposed method estimates the following performance measures. Kf ^f (te -e - ti-1 e- в-1) 1 - e - ^tk ^ e - ' - e - mvf = ap 1 - e Pptp where, α is a count of failures of the Goel–Okumoto (G-O) model αp is an estimation of total number of failures of the proposed model. β refers to the failure occurrence rate, t represents detection time and tp indicates total failure time Mean Value Function (MVF) is the cumulative number of failures detected between time 0 and t[25]. The proposed method is presented with following assumptions [26] 1. NHPP is used to model Failure observation and fault removal. 2. The learning capability of the Tester is an incremental function relevant to testing time. 3. Software failure and fault removal functions are independent of each other. 4. In a software system, the residual fault detection rate is a non-increasing function dependent on time. 5. The probability of occurrence of a failure is directly proportional to the number of undetected residual faults. C. Stopping Rules Stopping rules are vital to the development of software cost models. The Software testing process inherently is found to be expensive and consumes a major share of the software development project cost [27]. According to literature, many researchers have addressed the stopping rule problem. Several stopping criteria were compared to study their impact on product-release time: • Number of remaining faults: When a fraction ‘p’ of the total expected faults are detected, Testing can be stopped. • Failure intensity requirements: When the failure intensity is found to have a specified value at the end of the test phase, Testing can be stopped. • Reliability requirements: When the software development is in operational phase, if the conditional reliability reaches a required value, then the testing is stopped. This can also be expressed mathematically as the condition when the ratio of the cumulative number of detected faults at time T to the expected number of initial faults, reaches a specified value D. Optimal Software Release Time Like any traditional SRGM, the analyst has to design a model optimize it. The information obtained from the analysis has the potential to assist the management in taking crucial decisions with regard to the project. By incorporating the fault debugging time, it is possible to extract more practical data, which in turn could prove useful in decision-making. The proposed model can thus help us to realize the optimal software release time, subject to different software testing stopping criteria. E. Exponential Distributed Time Delay During the testing phase, the correction time is found to follow an exponential distribution, with an assumption that it is distributed as ∆≅exp(μ) at a given fault detection intensity of λd [28].The fault correction intensity is then expressed: Xc (t) = E[Xd (t - A)] = Jxd (t -xy^e-Axdx (7) The fault correction MVF for Goel-Okumoto model is expressed as: mc (t ) = a.[1 -(1 + bt)e bt a .[1e "bt + [ A - b b A - b e-At A = b A * b F. Normally Distributed Time Delay For a normal time delay distribution with mean µ,variance σ2and the fault correction density function λc, the fault detection intensity function λd is estimated with t . -(x - A )2 Xc ( t )= E [Xd ( t-A)]= fXd (t-x ).-K= e 2” 2 dx 2П” b2+2 Ab = abe 1 - -/ bt [^( t - A - b)-^(-A - b) (9) The fault correction process is then expressed as: t mc (t)= E[md (t A)^ JXc (t) t b2+2Ab -bt = 1 abe2 [^( t - a - b)-p(-A - b)] dt (10) IV. Results and Discussions Actual industrial data is used to experiment on the proposed model. The industrial data was gathered from an in-progress CMMI level 5 project. For this, two templates are used. The proposed method testing process is evaluated on the SAP system software failure data. It consists of failures per day over a period of 170 days. During this, the system is (kept) idle in the following days 121, 122, 128, 142, 143, 144, 145, 147, 148, 149 and 150. A new reliability estimation model was developed. While most estimation models are used in the later part of the testing stages, this one uses the characteristics of the initial testing stages. Estimation models are generally categorized as: a) Failure detection estimation models: Test time is factored in to these models to predict future failure trends by considering detected failure count per time interval. b) Failure removal estimation models: These models predict future failure removal using removed failures detected per time interval. Neither the testing activities nor the debugging activities of the developers are taken into consideration by either of these models. Exponential models form the basis for the proposed model, and hence data that fit into S-shaped models do not conform to the proposed model, which inadvertently shows the proposed model’s limitation. Fig.2. Weighted failure intensity of the proposed method Fig. 2 presents the weighted failure intensity of the proposed method. Fig. 3 shows the Cumulative Distribution Function (CDF) of the proposed method. The Fig. 3 explains the relationship between the failures and time of the proposed method. Fig.3. CDF of the proposed method. – Software failures vs. time. Fig. 4 shows the results of the proposed weighted Laplace trend compared with the conventional Laplacian approach. The result is illustrated in Fig. 4 reveals the efficiency of the proposed method. Due consideration is given to the system activity as well as the amount of reliability growth within the proposed model. This method is aptly called the generalized weighted Laplacian approach for NHPP models. This statistics based approach to assess reliability is found to be adequate, after considering the test results. Fig.4. Comparison Graph of Weighted Laplace Trend with Green’s function Performance analysis for this method is done using various measures discussed in section 2. Fig. 5 shows the plot of MVF values against time. The MVF values from the proposed method and NHPP model are compared as shown in Fig. 6, making it evident that the proposed method exhibits better efficiency. The Fig. 7 shows the actual and estimated faults identified in time ‘t’. The Mean Relative Error (MRE) and Mean Square Error (MSE) are used to compare and analyze the results against the actual data [25]. Various performance measures of the proposed method and the Goel-Okumoto (G-O) model are compared and shown in Table 1. Table 1. Comparison of G-O model and proposed Method Performance Measure Goel-Okumoto Model Proposed Method Time 1250 1250 Detection Rate α 12.34 12.34 Β 0.05 0.04 MRE 0.13 0.10 MSE 0.60 0.29 Total Intervals 38 38 Failures 10.56 10.10 Fig.6. Comparison of MVF measure of proposed and NHPP model Fig.7. Faults identified in time ‘t’ by the proposed method Table 1above shows that this method is more efficient than the G-O model. The performance is evaluated using the sum of square errors (SSE) which gradually decreases when compared to other models[26]. SSE presents the deviation of estimated number of faults detected totally from the actual number of faults, and is expressed as: n sse = ^( yt- m (ti ))2 i=1 Where ‘n’ represents the number of failures in the given dataset of yi at time ‘ti’. The smaller the value of SSE, the better the goodness of fit provided by the model [26]. Table 2. Dataset taken from [29] Test period CPU hrs Defects found (1) 520.0 17 (2) 968.0 24 (3) 1430.0 27 (4) 1893.0 33 (5) 2490.0 41 (6) 3058.0 49 (7) 3625.0 54 (8) 4422.0 58 (9) 5218.0 69 (10) 5823.0 75 (11) 6539.0 81 (12) 7083.0 86 (13) 7487.0 90 (14) 7846.0 93 (15) 8205.0 96 (16) 8564.0 98 (17) 8923.0 99 (18) 9282.0 100 (19) 9641.0 100 (20) 10000.0 100 Table 3. Comparison of models over SSE Models SSE values G-O model 155.50 S-model 825.00 Proposed model 147.20 Table 3 shows that, in the current experiment, the SSE value for the proposed NHPP model is lower than other models. From the results it is also clear that the number of residual faults within the software can be better predicted using the proposed NHPP model which is based on the fault detection rate and it fits best. A. Application of MVF to G-O Growth Model The G-O growth model is considered for quality assessment [26]. Assumptions for the G-O model: • G-O model is a NHPP • The fault detection rate value is a constant; • Software failure detection and fault removal process occur independent of each other. • For every occurrence of a failure, the cause (error) is identified and removed immediately, and no new errors take its place. • The probability of occurrence of a failure is proportional to the number of residual faults yet to be detected. • The probability of fault detection is proportional to the number of residual faults yet to be detected. Considering the above assumptions, the G-O model is expressed as: dm^! = b(a — m (t)) (12) When the above equation is solved m (t) = a (1 — e-bt) (13) Where ‘a’ denotes the number of faults is to be eventually detected. Parameter ‘b’ represents the fault detection rate. This proves that the probability of fault detection is invariable over time [26]. B. Efficiency Analysis Assuming the efficiency as ‘ϵ’ equation (13) can be expressed as: dm^ = b ( a — fm (t)) dt By solving the above equations we get m'(t ) = ^ (1 — e "(1—в) bt)?(15) Assuming a’ = -5—^ b’ = (1 — в)^ m ‘(t ) = a ‘(1 — e—bt) The fault removal efficiency does not have any major impact on the accuracy of reliability prediction of this model. V. Conclusions The present paper proposed a novel approach for improved G-O model that can takes care of faulty debugging. The proposed method considers both the residual faults and learning ability for yielding improved fault detection rate. The dependency relation between fault detection rate model and the time is also discussed. When compared to other models, the results of the proposed method show an improved goodness-of-fit.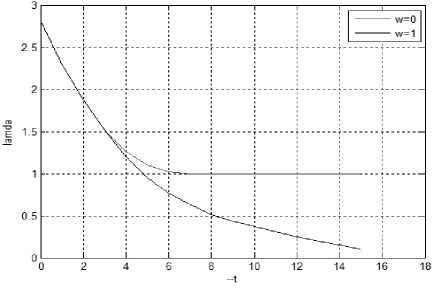
Список литературы Design of generalized weighted Laplacian based quality assessment for software reliability growth models
- Kan Stephen H., “Metrics. and Models. in Software Quality, Engineering”, Addison Wesley Longman Publishing, Boston MA, USA, 2002, ISBN:0201729156.
- ChinYu Huang,Kuo Sy-Yen,Michael Lyu, “An Assessment of Testing, Effort Dependent, SRGMs,” IEEE Transactions on Reliability, Volume: 56, Issue: 2, June 2007, Pages: 198–211, DOI: 10.1109/TR.2007.895301
- Deissenboeck Florian, Juergens Elmar, Lochmann Klaus, WagnerStefan, “Software, quality, models: Purposes, requirements & usage scenarios”, WOSQ‘09. ICSE Workshop,2009, Print ISBN: 978-1-4244-3723-8, DOI: 10.1109/WOSQ.2009.5071551
- Chin Yu Huang, “Performance analysis of SRGMS with testing-effort, and change-point”, Journal of Systems and Software, Volume76, Issue 2, (May 2005), Pages 181-194,DOI:http://dx.doi.org/10.1016/j.jss.2004.04.024.
- Shyur, H. J., “A stochastic software reliability model with imperfect-debugging and change-point”, Journal of Systems and Software, Volume 66, Issue 2, May 2003, Page(s): 135-141, DOI: 10.1016/S0164-1212(02)00071-7
- Kapur P. K.,Pham H.,Anand Sameer,Yadav Kalpana, “A Unified, Approach, for Developing, SRGMSs. in the Presence of, Imperfect, Debugging and Error, Generation,” IEEE, Transactions, on Reliability, Volume: 60, Issue 1, March 2011, Page(s): 331–340, DOI: 10.1109/TR.2010.2103590
- Bokhari M.U. and Ahmad N., “Analysis of a SoftwareReliability Growth Model: The Case of Log, Logistic Test Effort Function,” MS'06 Proceedings of the 17th IASTED international conference on Modeling and simulation, 2006, Pages 540-545,ISBN:0-88986-592-2, DOI: http://dl.acm.org/citation.cfm?id=1167209
- ShigeruYamada, “Software Reliability Modeling: Fundamentals, and Applications,” (Print)ISBN:978-4-431-54564-4,(Online)978-4-431-54565-1.
- Kapur P.K., Pham Hoang A., Gupta, Jha P.C., “Software Reliability, Assessment, with, OR Applications,” ISBN: 978-0-85729-203-2 (Print) 978-0-85729-204-9 (Online)
- Stefan Lessmann, Swantje Pietsch, Baesens Bart, Mues Christophe, “Benchmarking, Classification Models, for Software, Defect Prediction- A Proposed. Framework, and Novel Findings”, IEEE Transactions on Software Engineering, Volume 34, Issue 4, July to Aug 2008, Page(s): 485 – 496, DOI: 10.1109/TSE.2008.35
- N. Ahmad, Khan M.G.M., L.S. Rafi, "A study ,of ,testing effort ,dependent inflection S‐shaped SRGMs with, imperfect, debugging", International Journal of Quality and Reliability, Management, 2010, Volume27, Issue 1, pages: 89–110, DOI: https://doi.org/10.1108/02656711011009335
- Liebchen Gernot A, Shepperd Martin, “Data sets and Data Quality in Software Engineering”, PROMISE '08Proceeding of the fourth international workshop on Predictor models, in software engg. (PROMISE'08), 2008, ACM, New York, USA, pages: 39-44,DOI:http://dx.doi.org/10.1145/1370788.137079
- Afzal Wasif and Torkar Richard, “Review - On the application, of genetic, Programming, for software, engineering predictive modeling”, Expert Syst. Appl. 38, 9 (Sept 2011), 11984 to 11997, DOI=http://dx.doi.org/10.1016/j.eswa.2011.03.041.
- Samoladas Ioannis , Gousios Georgios , Spinellis Diomidis , Stamelos Ioannis , “The SQO-OSS Quality Model: Measurement Based Open source Software Evaluation,” Vol. 275,IFIP series: The International, Federation for, Information Processing, pp 237-248.
- Sharma Kapil,Garg Rakesh , Nagpal C.K.,Garg R.K., “Selection of Optimal SRGMs Using a Distance. Based Approach,” IEEE Transactions on Reliability(Volume: 59, Issue:2, June 2010 ), Page(s): 266 – 276.
- Ohishi Koji, Okamura Hiroyuki, and Dohi Tadashi. 2009. Gompertz software reliability model: Estimation, algorithm and empirical, validation, J. Syst. Softw. 82, March 2009, 535-543. DOI=http://dx.doi.org/10.1016/j.jss.2008.11.840.
- Huang Chin Yu,Lyu Michael R., “Estimation & Analysis of Some Generalized Multiple, Change, Point Software Reliability Models,” IEEE Transactions on Reliability ( Volume: 60, Issue: 2, June 2011), Page(s): 498 – 514.
- Huang Chin Yu, Hung Tsui-Ying, “Software, reliability, analysis and assessment using queuing. models with multiple. change points”, Vol. 60, Issue 7, October 2010, Pages 2015–2030.
- Li X., Xie M., Ng S.H., “Sensitivity analysis of release time of software reliability models incorporating testing effort with multiple change-points”, Applied Mathematical Modeling, Volume 34, Issue 11, November 2010, Pages 3560-3570, DOI: https://doi.org/10.1016/j.apm.2010.03.006
- Kalaimagal Sivamuni and Srinivasan Rengaramanujam, 2008, A retrospective,. on software, component quality models, ACM SIGSOFT Engg. Notes, Volume 33, Issue 6 (October 2008), Pages 1 to 10,DOI:http://dx.doi.org/10.1145/1449603.1449611.
- Saied A. Keshtgar, Bahman B Araseh , “ Enhancing software reliability against soft error using minimum redundancy on critical data “, I.J.Computer Network and Information Security, 2017, 5, 21-30, May 2017, in MECS (http://www.mecspress.org/), DOI: 10.5815/ijcnis.2017.05.03
- Mohd. Anjum, Md. Asraful Haque, Nesar Ahmad, “Analysis and Ranking of Software Reliability Models Based on Weighted Criteria Value”, I.J. Information Technology and Computer Science,2013, 02,1-14, January 2013 in MECS (http://www.mecspress.org/) DOI: 10.5815/ijitcs.2013.02.01
- Luo Yan, Bergander Torsten, Hamza Ben A., Software Reliability Growth Modeling using a Weighted Laplace Test Statistic, Computer Software and Applications Conference, 2007. COMPSAC 2007. DOI: 10.1109/COMPSAC.2007.194
- Krishna B. Misra, Handbook of Performability Engineering, Springer, London, 2008, Print ISBN 978-1-84800-130-5, Online ISBN 978-1-84800-131-2, DOI https://doi.org/10.1007/978-1-84800-131-2
- Akana Chandra Mouli Venkata Srinivas, Divakar C., Satyanarayana Ch., “Adaptive Mean Value Function Based Quality Assessment of Software Reliable Growth Models”, Computer Engineering and Intelligent Systems, IISTE, Volume 5, Issue 3, (March 2014), Page(s): 43-49, ISSN 2222-1719 (Paper) ISSN 2222-2863 (Online), DOI: http://www.iiste.org/Journals/index.php/CEIS/article/view/11689/12033
- Akana Chandra Mouli Venkata Srinivas, Divakar C., Satyanarayana Ch., “Residual Fault Detection and Performance Analysis of G-O Software Growth Model”, Journal of Current Computer Science and Technology, Volume 5, Issue 3, March 2015, pages(s): 5-7, DOI: http://innovativejournal.in/index.php/ajcem/article/viewFile/44/37
- Lyu M.R., Kuo Sy-Yen, Huang Chin-Yu, "Effort-index-based software reliability growth models and performance assessment", Proceedings 24th Annual International Computer Software and Applications Conference COMPSAC2000, 2000, DOI: 10.1109/CMPSAC.2000.884764.
- Xie M., Hu Q. P., Wu Y. P., Ng S. H., A study of the modeling and analysis of software fault-detection and fault-correction processes, Wiley Online Library, 2006, Pages: 459–470, DOI: 10.1002/qre.827.
- AIAA/ANSI “Recommended Practice for Software Reliability, the American Institute of Aeronautics and Astronautics”, Washington DC, Aerospace Center, R-013, 1992,-ISBN 1-56347-024-1.


