Design of Type-2 Fuzzy Controller based on LQR Mapped Fusion Function

Published Online July 2012 in MECS

The fuzzy logic based systems exhibit some characteristics that the classical control systems (PI, PD and PID) don’t have, like smoother control, noise immunity, little mathematical knowledge of the model behavior; uncertainty handling and they can obtain results from expert knowledge. This method has found applications in an incredibly wide range of areas in the relatively short period of time since its conception. This is because fuzzy logic, combined with the paradigm of computing with words, allows the use and manipulation of expert knowledge and reasoning in the modeling and control of complex dynamical systems. The ongoing research and applications in this field demonstrate the power and versatility of fuzzy logic.

The concept of information is fully connected with the concept of uncertainty. The most fundamental aspect of this connection is that the uncertainty involved in any problem-solving situation is a result of some information deficiency, which may be incomplete, imprecise, fragmentary, partially reliable, vague, sometimes contradictory, or deficient in some other way. The concept of fuzzy reasoning may allow handling much of this uncertainty. When something is uncertain, it is difficult to determine its exact value, and of course type-1 fuzzy sets make more sense than using simple sets (Zadeh, 1975[2]). However, it is not reasonable to use an accurate membership function for something uncertain, so in this case we need another type of fuzzy sets, which can able to handle these uncertainties, the so called type-2 fuzzy sets (Mendel, 2001[3]). In engineering as well as in the scientific field, there is growing interest to use type-2 fuzzy logic controller (FLC). Because uncertainties are inseparable from real systems, the research of novel methods to handle incomplete or not too reliable information is of great interest (Mendel, 2001[5]).

The application of fuzzy control to large-scale complex systems is not a trivial task. Large-scale systems require special approaches for modeling and control. Generally, the number of control rules of fuzzy controller, with the number of input variables, will increase exponentially. For instance, there are n input variables, correspondingly each variable is divided into m fuzzy sets in its fuzzy universe, and then the total rule number will reach mn, and is so called “rule explosion” problem. The high number of controller input dimensions as well as the excessive inference rules may reduce the inference speed even affect the inference correctness, degrade the controller's performance, and cause great difficulty to the design. Taking these factors into account, it is always a focus research of fuzzy theory scholars to reduce fuzzy controller's dimensions and the number of fuzzy inference rules. To overcome the problem, the idea of using hierarchical structure in designing a fuzzy system has been reported by Raju and Zhou [6,7], where the input variables are put into a collection of low-dimensional fuzzy logic units (FLUs) and the outputs of the FLUs are used as the input variables for the FLUs in the next layer. In [8], to solve the rule explosion problem in multi input fuzzy logic system, a method of converting the given fuzzy system to 2 layered hierarchical fuzzy systems is presented by considering the fuzzy rules as fuzzy rule vectors.

In [9-12], a method was proposed to automatically estimate the corresponding parameters for the sensory fusion method are found through the use of genetic algorithms. There are many ways can be used to achieve fusion function. In[13,14], the mapping of LQR (linear- quadratic regulator) gains is used to extract the features of LQR controller design in modern control theory as well as to reduce the dimensions for fuzzy controller input resulting the reduction of rule base to a great extent and applied to double inverted pendulum control. The same idea was implemented in[15] to design a DSP chip based real-time motion control for rotary inverted pendulum system.

In our work, the sensory fusion method is studied in an attempt to reduce the size of the inference engine for large-scale systems and LQR gain mapping based fusion method is simultaneously combine to apply in type 2 fuzzy controller system design such that the uncertainties in the model can be much better handled.

Also, Jamshidi proposed to use the combination of hierarchical and sensory fusion methods. In [9-12] the method consists in combining variables before providing them to input of the FLC. These variables are often fused linearly. For example, we want to fuse two input variables y1 and y2 (see Fig. 1). The fused variable Y will be calculated as Y = ay 1 + by 2 . Here, it is considered that the input variables of the fuzzy controller are represented by m = 5 linguistic labels. Therefore, in this case, the number of rules will be thus reduced from 25 to 5. As we can observe, more variables has the fuzzy controller, more reduction can be obtained. The reduction of the number of rules is optimal if one can fuse all the input variables in only one variable associated. In this case, the number of rules is equal to the definite number of linguistic labels for this variable. But it is obvious that all these variables cannot be fused arbitrarily, any combination of variables has to be reasoned and explained.

Ledeneva(2007a,b[11,12]) proposed a hierarchical scheme whose goal is to minimize the number of fuzzy rules from exponential to linear function. Such rule base reduction implies that each system variable provides one parameter to the hierarchical scheme. Initially, the selection of such parameters was manually done. The disadvantage of the design of hierarchical and sensory fused fuzzy controllers is that much reliance has to be put on the experience of the system designer to establish the needed parameters. To solve this problem, GA was used to automatically estimate the parameters for the hierarchical method [17].

Since, the above stated methods need to calculate the parameters associated with each fuzzy and the corresponding fusion block, so GA maybe one of the best method to automatically estimate these parameters. But, it is very tedious job to apply this technique, especially for the beginners. Hence, there is need to apply a method which should be based on the basic ideas in control theory and easy to apply.

• II.    Sensory Fusion Method

Jamshidi[19] first proposed to use sensory fusion(Fig.1) which combines several inputs into one single input to FLC. However, the fusion technique synthetically deals with the information which comes from multiple sensors or different sources, therefore more accurate and more reliable conclusions will be obtained. This method reduces the number of rules considerably. But, in order to do so, the adequate parameters should be estimated, which, in the traditional way, depends on the experience and knowledge of a skilled operator.

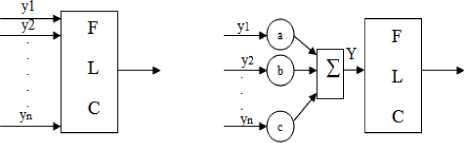
Fig.1. Rule base reduction of sensory fusion fuzzy controller

• III.    LQR Mapping Based Information Fusion

In this paper, since the basic aim is to use the features of LQR control technique of modern control theory in fuzzy controller design for complex system, which is only applicable to linear state-space model, so we need to first model the linear state-space of the system or plant.

Define the system's state space equation as:

X = AX + Bu Y = CX + Du

Choose the quadratic objective function as:

J = 1 J ( X T QX + u T Ru ) dt        (2)

Weighting matrix Q and R are used to balance the weight of the rotary inverted pendulum system state- vectors X and u. Because of Q being a semi-definite matrix and R being a definite matrix, the objective function is non-negative. On output disturbances affecting the system, give an appropriate u that is called optimal control to make the system return to equilibrium position as soon as possible and at the same time make the objective function is minimum.

Fusion function design steps [13] combining with optimal control are given as follow:

Table 1: The No. Of Rules For Different Reduction Methods

Method used to reduce the no. of rules	The no. of variables n >1
	Even	Odd
Sensory fusion	mn/2	m(n+1)/2
Hierarchical	(n-1).m2
Combinational	((n/2)-1).m2	((n+1)/2)-1).m2
LQR-fusion	2 m

• •    Calculate the state feedback matrix K by selecting appropriate value of Q and R matrix that can make the system basically stable through LQR theory.

• •    Construct fusion function F I (X) using state feedback matrix K and it is described as (3):

1 K

F ( X ) = — q

I K I 0

q ₁

Where, nn

II K = 1 E ( K . )^{2 +} Z ( K ) 2 ]            ⁽⁴⁾

• Reduce the dimensions of input variable:

^X = ^[ q 1 , q 2 ^..-, q n , q 1 , q 2 ^..., q n ^]

By F I (X), and obtain the comprehensive error E , error change rate EC expressed as (5):

E

EC

= F 1 ( X ) X T

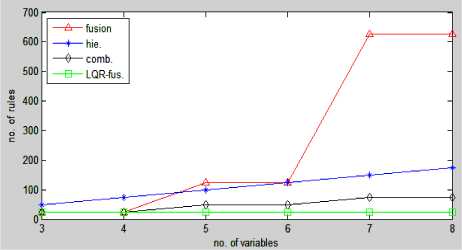
Fig.7 Comparision of various rule base reduction methods with m=5

IV. Interval Type-2 Fuzzy Logic

The type-2 fuzzy sets are used to model the uncertainty and inaccuracy in real-world problems. This set was originally proposed by Zadeh in 1975 and are essentially "fuzzy-fuzzy" sets in which grades of membership are type-1 fuzzy sets. A type-2 fuzzy set expresses the degree of non-determinist truth with vagueness and uncertainty with which an element belongs to the whole set.

If f_x ( u ) = 1, V u g [ J U , J u ] c [0,1]

Since, there are only two input to the fuzzy controller of the form of error E and error deviation EC i.e. fixing n=2 , so the no. of rules can be formulated as m² .

Table 1 and chart given below show the comparative study of the all type of rule-reduction methods stated above.

An interval type-2 fuzzy set (IT2FS) Ã is characterized as:

A =f f X 4= ([   [/]/ x    (6)

(x, u)              u xGX UGJxc[0,1]               XGX UGJxc[0,1]

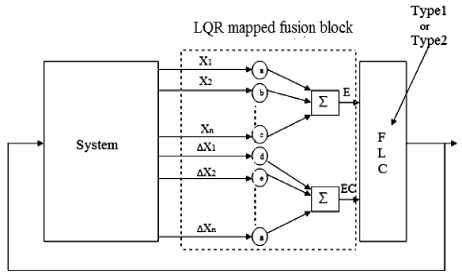
Fig.6 Basic block diagram of LQR-Fusion based FLC

Where x , the primary variable, has domain X; u G U, the secondary variable, has domain Jx at each X G X; Jx is called the primary membership of ~ x and, the secondary grades of A all equal 1. Note that (6) means A : X ^ {[a,b]: 0 < a< b< 1}.

Uncertainty about à is conveyed by the union of all the primary memberships, which is called the footprint of uncertainty ( FOU ) of à . The grey area (Mendel, 2000), and this is bounded by an upper and a lower membership function as shown in Fig. below, i.e.

FOU ( A ) = U v x g x J x = {( x , u ): u g J x c [0,1]}      (7)

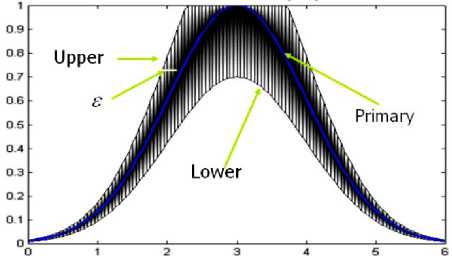
Fig.8. FOU (gray area), LMF, UMF and primary MF (central line) for IT2FS[26].

m             m (            Г p I            h^

Цв (У) = П Цв- (У) = П Цв- (У)П 1 П LEax, (Xi ) Jr i=1                 i=1 \                 I i=1                 J у

= \ ц _в ⁽ У ) Ц в ⁽ У ^{) ]}

where

M

Ц в ⁽ У ) = ^( Ц в -

M ⁽Г p(        ,~

Д Ц а х , ^{( х )} * Ц р - kL

^

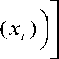
* ^Ц - ⁽ У )

G    у

The upper membership function (UMF) and lower membership function (LMF) of à are two type-1 MFs that bound the FOU (Fig. 8).

Ц в ⁽ У ) = у ⁽ Ц в - ⁽ У ) )

^M (Г pi-      ~

= м   ^Ц^х 1⁽ X ) *

kL

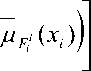
~ Ц - ⁽ У ) У

• A. Type-2 fuzzy reasoning

Assuming a fuzzy system with M rules, p input variables and one output variable, we have that the antecedent and consequent are type-2 fuzzy sets.

R¹: IF x₁ is F ¹ and…and x_p is F ¹ THEN y is G ¹

• H: x₁ is A and…and x_p is A x ₁                          x_p

c: y is y ˆ                                                (8)

This reasoning evaluation is:

The k-th rule relation its

B = A_xoR^l , Generalized, fuzzy reasoning

The interval type-2 fuzzy reasoning is depicted in Fig. 9.

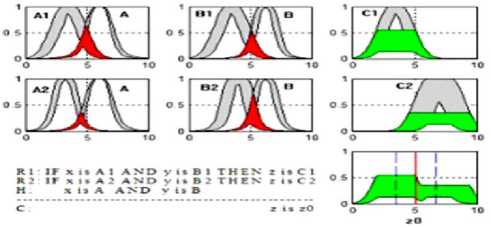
Fig.9 interval type-2 fuzzy reasoning[1]

Ц в. (У) = MA oR1 (У) = П eX Lea (X)П ^Al^d (X, У)J xx

Ц в ( У ) = Ц G l ( У ) П fc L ^Ax, ⁽ X ) П Ц р - ⁽ X ) J }

= Vb' ( У ), Ц в - ( У ^{) ]}

Where

Ц в -

p

~

*1 ^{Ц (} X ) * M_F I ^{( X} i )

t = 1^-- ^AX 1            -- F i

~ Eg - ⁽ У )

Ц в - =

p _~

_;* \M a_X1 ^{( X} i ) * Ц р - ^{( X} i ) )

* E g - ⁽ У )

B. Type-2 rule based fuzzy logic system

IT2FLC design is based on the concept of interval type-2 fuzzy logic system. The structure of IT2FLC is same as the conventional fuzzy logic controller structure except, one type reducer block is introduced between the inference engine and defuzzifier block because the output of the inference engine is a type-2 output fuzzy set and before applying it to the defuzzifier for getting the crisp input it has to be converted to a type-1 fuzzy set. A Fuzzy Inference System is a system based on fuzzy rules, instead Boolean logic, to data analysis [2]. Its basic structure includes four principal components, as shown in Fig. 10.

• 1.    Fuzzifier :- Map inputs (crisp values) into fuzzy values

• 2.    Inference System :- Applies a fuzzy reasoning to obtain a type-2 fuzzy output.

• 3 .    Defuzzifier/Type Reducer :- The defuzzifier maps an output to a crisp values; the type reducer transform a type-2 fuzzy set into a type-1 fuzzy set.

• 4.    Knowledge Base : - Contains a fuzzy rule set, known as the base of rules, and a membership function set known as a database.

Aggregation

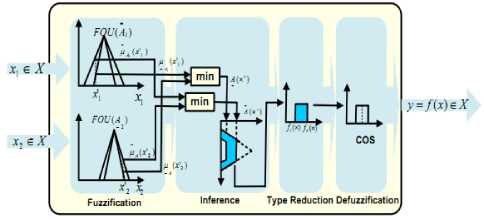
Fig.10. Interval Type-2 Fuzzy Logic controller[25]

• V.    Case Study: Modeling and Characteristics

Analyzing of Linear 1-Stage Inverted Pendulum

• A.    Inverted pendulum structure

The inverted pendulum system is composed of a cart moving on guideway[21] and a pendulum which is fixed on the cart. The displacement of the cart can be measured by a sensor installed on one side of the guideway, and the angle signal can be measured by a coaxial angle sensor install in the bearing which articulates the pendulum to the cart. On the other side of the guideway is mounted a DC permanent magnetic direct torque motor, driving the cart to move on the guideway. The cart that is shown as Fig. 11 is controlled by the function F=u(t) moving in the x- axis direction to keep the pendulum stable in the perpendicular plane.

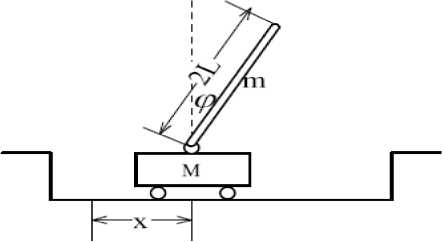
Fig.11. Inverted pendulum system sketch

The cart is restricted to move within a fixed range. The reference position for x is 0 meter , when cart is in the center of the chosen basic universe of discourse; and for ϕ(θ) is π ( zero ) rad , when the pendulum is at a natural stable downward position. The motor input voltage range is -5 V to +5 V .

• B.    Mathematical model of Inverted pendulum

  In this paper, the IP system, by Googol’s GLIP2001[22] model, can be viewed as a rigid-body system of cart-pendulum when neglecting air resistance and various frictions. Build the one stage linear IP mathematical model near its vertical upright balanced state, the dynamic equations of the system can be found with help of the Euler-Lagrange equation as:

( M + mx + bx + mL6 cos 6 — mLO¹ sin 6 ) = F

( I + mL 2^6 + mgL sin 6 = — mLx cos 6      (11)

Table 5 shows the parameters of the inverted pendulum used in the model. The linearized form of nonlinear system is derived, taking the state variables:

x_x = x , x₂ = x _i, x₃ = ф , x ₄ = ф

Gate the state space equation as (1) where,

A =	■ 0 0	1 0	0 0	0" 0	, B =	" 0 " 1	(12)
	0	0	0	1	,	0
	_ 0	0	29.4	0 J		_ 3 J
	"1	0	0	0 1	" 0 1
C =					D =
	_ 0	0	1	0 _,J	_ 0 J

It is easy to obtain the state controllability expression of IP system and it is as (13)

rank [ B AB A ² B AB ] = 4       (13)

And the output controllability expression of IP system is rank [ CB CAB CA2 B CA B D ] = 2  (14)

As for the inverted pendulum system obviously, the rank of state matrix equals to the number of system’s state variables, and they are all 4. At the same time the rank of output matrix is 2 as well as the output variables ( x and ϕ ) are. Therefore states and output of the approximate linear time-invariant system are absolutely controllable, and it is possible to make the system stable through designing specific controller.

• VI.    Implementation of Information Fusion

Inverted pendulum system is a multi-sensor system; multi-sensor is the basis of information fusion, and multi-source information is its object. The information fusion is that the multiple sensor or multi-source information is treated comprehensively, in order to obtain more accurate and reliable conclusion [13].

It is well known that the linear system has characteristics of direct integration, so the inverted system state variables can be changed into integrated error E and error change EC by constructing a linear fusion function by following the designing steps in section III earlier. In this paper, construct a linear fusion function on the basis of LQR control.

Define the inverted pendulum system's state space as in (12).

• •    Calculate the state feedback matrix K that can make the inverted pendulum system basically stable through LQR theory. For, R =1 and Q =[1000 0 200 0] ;

K = [-31.623 -20.151 72.718 13.155].

• Construct fusion function F I (X) using state feedback matrix K and it is described as (15):

u ^U ( FIS 1) ⁺ u ( FIS 2)₂

^{F 1 (} X )=1 \K\ IL 0

x

k

KK x     ф

Where,

II K = V [( ^K x ) 2 + ( ^К Ф ) 2 + ( K )² + ( К ф )² ]    ⁽¹⁶⁾

The fusion function F I (X) based on state feedback matrix K is calculated as:

F i ( X ) =

- 0.38164

0.8776

- 0.2432

- 0.15876

Fuzzy controller design with fusion:

A. Fuzzy field selection

The actual ranges of fuzzy controller input variables E and EC are called basic universe. Variables within the basic universe are accurate values. The basic universe choice of variables E and EC depends on controlled objects. Change the basic universe of variables E and EC into the fuzzy universe through quantization factors. Increasing the number of fuzzy sets in the fuzzy universe can improve control accuracy, however, correspondingly the calculation will be increased and the reasoning speed will also be reduced.

• •    Reduce the dimensions of input variable:

X = [ x , ф , x , ф ]

By F I (X), and obtain the comprehensive error E, error- change rate EC expressed as (17):

E

EC

= F 1 ( X ) X T

• VI I. Fuzzy Controller Design

Fuzzy controller design without fusion:

Considering a four input and single output inverted pendulum, now using equation below to form control law as:

u = - Kx - K₂x ₂ - K₃x ₃ - K₄x₄        (18)

Equation (18) is then mapped onto a fuzzy inference system. Using same method for a five membership function and four input system, the number of rules obtained is 625. When this was implemented using Matlab/Simulink, together with the Real Time Workshop, the Fuzzy Logic Toolbox and the FIS compilation was extremely slow as the RAM memory requirement increases with the number of membership functions. To overcome such a limitation, we can divide the fuzzy control law into two subsystems, one taking inputs from the cart, and the other one taking inputs from the pendulum. The feedback control signal is calculated by adding together the outputs of the two FIS. For the cart subsystem, which has two inputs and one output, FIS1 approximates the linear equation:

u_x =- Kx - K₂x₂            (19)

Similarly, the pendulum subsystem is a two input single output system, and FIS2 approximates the linear equation:

u ₂ =- K₃x₃ - K₄x₄            (20)

Finally, the outputs of two FIS’s are added to derive a single control signal

• B.    The definition of membership function

For both type1 and type2 fuzzy controller design, define five fuzzy sets in the fuzzy universe [-1 1] for error E , error change EC and u . And these fuzzy sets are described with linguistic variables NB , NS , Z , PS , and PB respectively representing negative big, negative small, zero, positive small, positive big. In the paper, we have used overlapping and uniformly distributed triangular-shaped membership functions (MFS) describing fuzzy sets shown as Fig. 14 & 15:

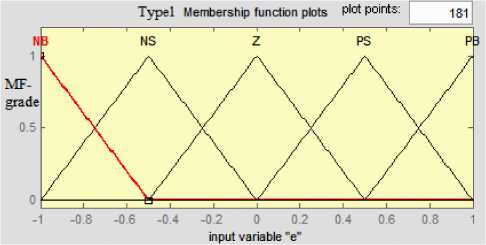
Fig.14. The type-1 fuzzy membership functions distribution

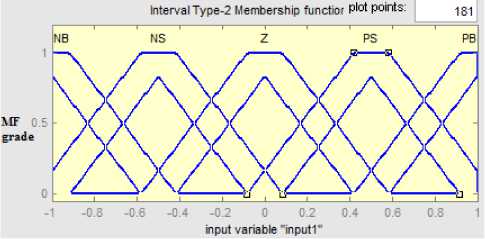
Fig.15. The type-2 fuzzy membership functions distribution

In order to improve control sensitivity and response speed, it is very important to apply triangular shaped member functions with well effective real-time feature and high resolution in the smaller margin of error[19].

Since, the increase in number of MFs may result better quality control because UOD contains more fuzzy variables. But due to the exponential growth of fuzzy rules, especially when there are more than 2 states like in IP, DIP it is 4 and 6 respectively have to control, the memory allocation by fuzzy is large and causes shut down the computer. While in case with fusion, due to fewer rules (m2 with fixed n=2), the problem of memory allocation can be easily handled and this will ensure real-time practicability of these type of complex systems.

• C.    The establishment of fuzzy rules

Input variables E and EC mentioned before are all divided into five fuzzy sets in their fuzzy universe.

Correspondingly 25 control rules, shown in Table 2, are:

Table2 fuzzy Control Rules

U		EC
		NB	NS	Z	PS	PB
E	NB	NB	NB	NB	NS	Z
	NS	NB	NB	NS	Z	PS
	Z	NB	NS	Z	PS	PB
	PS	NS	Z	PS	PB	PB
	PB	Z	PS	PB	PB	PB

The Mamdani type of inference method and c.o.g defuzzification method, based on the established rules, are chosen to turn the fuzzy output into the precise value needed by the inverted pendulum system. The fuzzy control surface is obtained as:

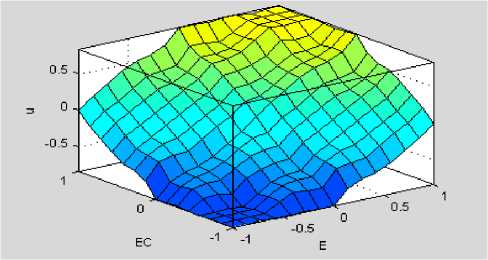
Fig.16. Nonlinear control surface of mapped type-1 and type-2 FIS

• VIII.    Simulation Results And Analysis

The design is tested in MATLAB with SIMULINK [24] environment. During debugging process, the given initial states of inverted pendulum including the cart displacement and pendulum angle will especially affect the system's stability. Assume pendulum angle deviating from the vertical upright direction as ϕ , we have done several experiments to show the performance of our control system. It is to be noted that, when we choose the solver as variable step ‘ ode45’ , the response due to fuzzy get much slower so, the sampling time of 0.01 s with solver ‘ ode3’ is chosen throughout the experiment.

For evaluating the transient closed-loop response of a computer control system we can use the same criteria that normally are used for adjusting constants in PID controllers namely IAE, ISE, ITAE[26].

The 1^st experiment is to check the performance of LQR controller with different sets of Q and R matrix keeping in mind that the priority to be given more to control pendulum angle compared to cart displacement. The simplest case is assumed R = 1, Q = C T * C . The expected response could also be achieved through adjusting the controller by changing nonzero element in matrix Q.

Q = C T * C

In which, Q 11 is the cart position coefficient, Q 33 is the pendulum rod angle coefficient, and the input coefficient R is 1.

From below figure, it is clear that the system will be more robust to disturbance and the settling time will be shorter if Q is larger (in certain range). But, we can’t take too large value of Q value, because in this case the system response becomes too faster that can’t be realizable.

Basic block diagram of LQR-Fusion based Fuzzy controller structure is given in Fig.6, where, Ke , Kec are taken as 1 and Ku equal to 80 for type1 and 600 for type-2 FLC.

Table 3: Comparison Of FLC With And Without Fusion

Sl. no.	properties	Fuzzy controller design Without fusion	Fuzzy controller design With fusion
1.	No. of rules	50 with m=5, n=4	25 with m=5, n=2
2.	No. of scaling parameters	6 (very difficult to adjust)	3 (less difficult to adjust)
3.	Complexity	more	less
4.	Real-time realization	Very difficult, very slow	Easy, faster

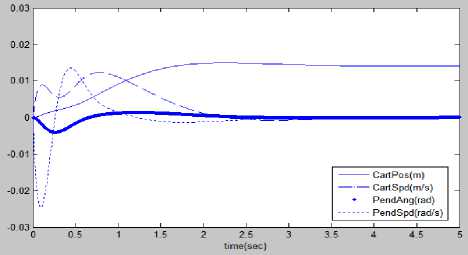
Fig.17 Optimal LQR controlled IP state response when (a)Q 11 =10,Q 33 =10

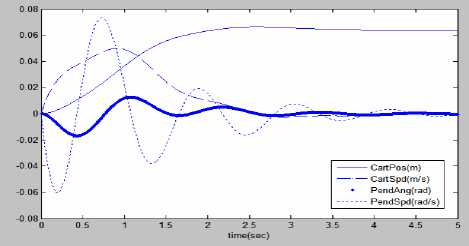
Fig.17 Optimal LQR controlled IP state response when (a)Q 11 =10,Q 33 =10 (b)Q 11 =1000,Q 33 =200.

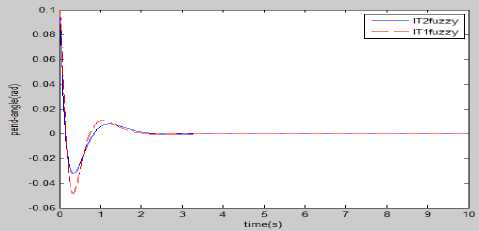
Fig.19. Simulation results comparison of fuzzy controllers for pendulum angle without disturbance.

Providing control input as a step input in LQR control structure and best of the result obtained from different sets of Q will be used to compare the various control performance such as settling time, steady state error, overshoot and disturbance rejection capability with fuzzy control. Fig. 18 shows the step response of the system with LQR without any disturbance.

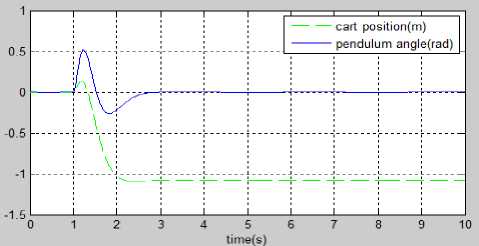
Fig.18. Stabilization of IP using LQR control

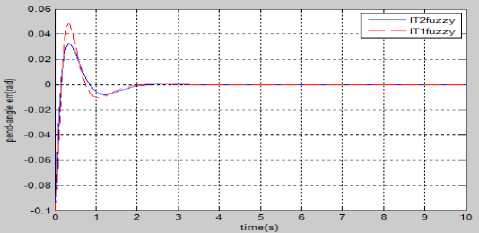
Fig.20. Simulation results comparison of fuzzy controllers for pendulum angle error without disturbance.

In the 4^th experiment, a disturbance of amplitude 2 V for time-interval 4-6 s is superposed with the control input and the comparative results of fuzzy controllers are analyzed. It is depicted from Fig. 21 that Type-2 has better control performance than Type-1, because the state’s response are comparatively less affected due to disturbance and rapidly settled to equilibrium position in case of fuzzy control.

We can see that the LQR control is able to stabilize the pendulum angle within 3s with zero steady-state error, hence the design criterion is satisfied.

In the 2nd experiment, linear fusion using LQR mapping without fuzzy controller is tested which results exactly same performance as LQR. This reveals that, the role of fusion function is just to reduce the dimension of inputs to the controller, whereas the controller part is nothing but LQR gain in modified form. Also, since LQR-mapped fuzzy controller extracts the features of LQR technique, so here no need to compare LQR performance with that of fuzzy controllers.

In the 3rd experiment an ideal condition i.e. no any external disturbance is introduced and the comparative results of fuzzy controllers are analyzed. It is depicted from Fig. 19 that Type-2 has better control performance than Type-1, because, there is negligible damping in steady-state part and comparatively less overshoot present in the transient part of the state’s response in case of fuzzy control.

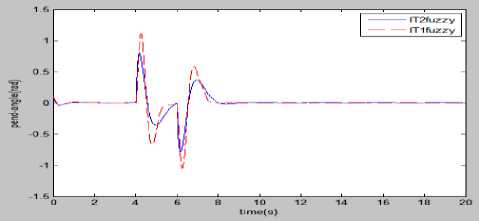
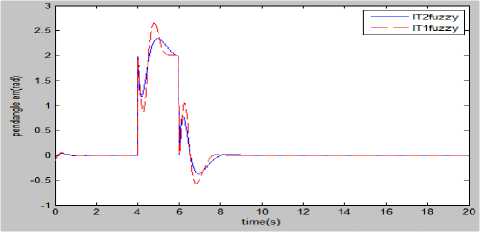
Fig.21. Simulation results comparison of fuzzy control for (a) pendulum angle, (b)pendulum angle error when a short duration disturbance is superposed with control input.

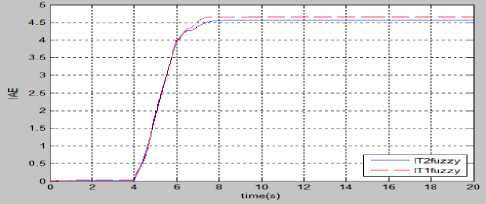
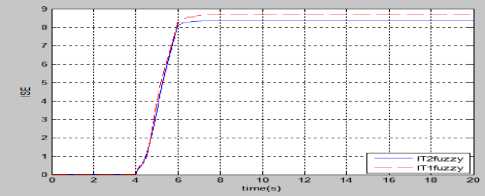
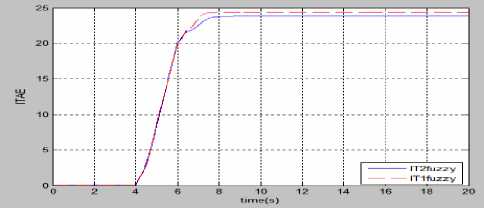
Fig.22. Performance comparison of fuzzy controllers for (a) IAE (b) ISE (c) ITAE, when a short duration disturbance is superposed with control input.

In the 5^th experiment a disturbance of amplitude 2 V for time-interval 4-6 s and a random disturbance of amplitude 0.1 V and frequency 1 Hertz is superposed with the control input and the comparative results of fuzzy controllers are analyzed. It is depicted from Fig. 23 that Type-2 has better control performance than Type-1, because, there is comparatively less overshoot present in the transient part and small damping in the steady-state part of the state’s response in case of Type-2 fuzzy control.

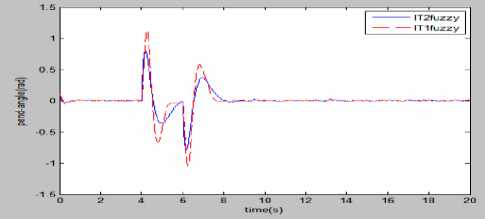
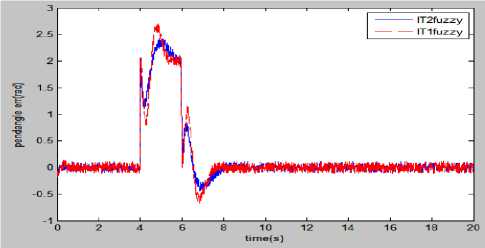
Fig.23. Simulation results comparison of fuzzy control for (a)pendulum angle, (b)pendulum angle error, when a short duration pulse with random disturbance is superposed with control input.

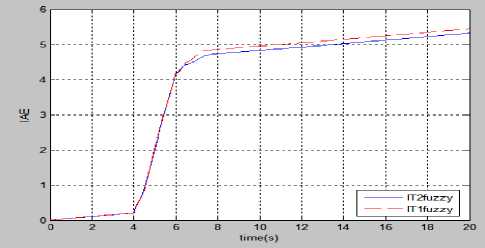
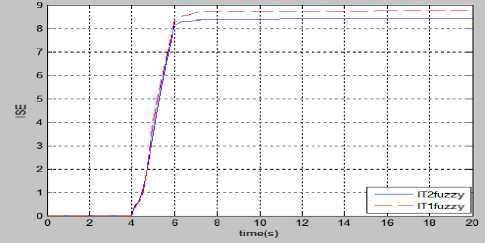
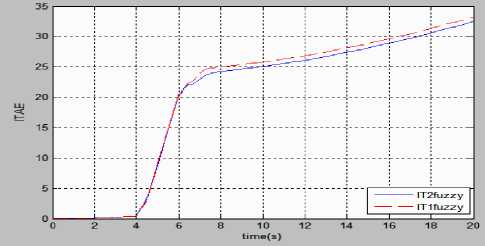
Fig.24. Performance comparison of fuzzy controllers for (a) IAE (b) ISE (c) ITAE, when a short duration pulse with random disturbance is superposed with control input.

The last three experiments show the excellent robustness of fuzzy controller.

The comparison on the basis of performance criteria such as IAE, ISE, and ITAE correspond to pendulum angle error also support that the control quality obtained in case of type-2 fuzzy is better than type-1 fuzzy control.

Disturbance		ISE		IAE		ITAE
		T1FIS	T2FIS	T1FIS	T2FIS	T1FIS	T2FIS
1	2V,4-6s	8.6761	8.3672	4.6492	4.5599	24.366	23.876
2	Random 0.1v,1Hz&2V,4-6s	8.752	8.4243	5.4427	5.3189	33.2361	32.4875
3	ideal	0.0013	0.000854	0.0322	0.0265	0.0159	0.0149

The selection of the criteria depends on the type of response desired, the errors will contribute different for each criterion, so we have that large errors will increase the value of ISE more heavily than to IAE. ISE will favor responses with smaller overshoot for load changes, but ISE will give longer settling time. In ITAE, time appears as a factor, and therefore, ITAE will penalize heavily errors that occur late in time, but virtually ignore errors that occur early in time [26].

• IX.    Conclusion And Future Work

For real systems, systems with uncertainty, we observed and quantify that the lower overshoot errors and the best settling times were obtained using a type-2 FLC. We are concluding that using a type-2 FLC in real world applications can be a better choice since the amount of uncertainty in real systems most of time is difficult to estimate. In this paper, an LQR-mapped linear fusion function is utilize to reduce the large number of fuzzy rules called “rule-explosion problem” to a precise set of rules and then applied to design an interval type-2 fuzzy controller for a complex system in order to handle the uncertainty in the model. The method has been applied to the approximate linear model, and the experimental results (qualitative and quantative) show that this method has better tracking performance, disturbance resisting capability, and robustness against model uncertainties.

Appendix

Table 5: Parameters Of IP Equations [22]

Parameter	Definition	Value	Unit
g	Gravity constant	9.81	N/Kg
M	Mass of cart	1.096	Kg
m	Mass of rod	0.125	Kg
b	friction coefficient of the cart	0.1	N/m/s
L	distance from rod rotation axis center to rod mass center	0.25	m
I	Inertia of rod	0.0034	Kg m2
x	Cart displacement	..	m
x	Cart velocity	..	m/s
x	Cart acceleration	..	m/s2
ф or (п- 0)	Deflection of pendulum	..	rad
φ	Velocity of pendulum	..	rad/s
φ	Acceleration of pendulum	..	rad/s2
u	Cart acceleration(as input)	..	m/s2

Acknowledgment