Design Parallel Fuzzy Partly Inverse Dynamic Method plus Gravity Control for Highly Nonlinear Continuum Robot

Published Online December 2013 in MECS

Controller is a device which can sense information from linear or nonlinear system (e.g., continuum robot) to improve the systems performance [7-9]. The main targets in designing control systems are stability, good disturbance rejection, and small tracking error[7-12]. Several continuum robot are controlled by linear methodologies (e.g., Proportional-Derivative (PD) controller, Proportional- Integral (PI) controller or Proportional- Integral-Derivative (PID) controller), but when robot works with various payloads and have uncertainty in dynamic models this technique has limitations. In some applications continuum robot are used in an unknown and unstructured environment, therefore strong mathematical tools used in new control methodologies to design nonlinear robust controller with an acceptable performance (e.g., minimum error, good trajectory, disturbance rejection) [8-10]. Advanced control techniques such as sliding mode controller, feedback linearization methodology, adaptive and robust have been applied to the control of numerous single- axis machines and robotic manipulators. Inverse dynamic method is an influential nonlinear controller to certain and partly uncertain systems which it is based on system’s dynamic model. Inverse dynamic methodology is a powerful nonlinear robust controller under condition of partly uncertain dynamic parameters of system [7]. This controller is used to control of highly nonlinear systems especially for continuum robot manipulators. Nonlinear equivalent dynamic formulation in uncertain dynamic parameter is the main drawback in pure inverse dynamic controller [12-16]. The nonlinear equivalent dynamic formulation problem in uncertain system is solved by using soft computing theory [17-22]. Although the fuzzy-logic control is not a new technique, its application in this current research is considered to be novel since it aimed for an automated dynamic-less response rather than for the traditional objective of uncertainties compensation[23-36]. The intelligent tracking control using the fuzzy-logic technique provides a cost-and-time efficient control implementation due to the automated dynamic-less input. This in turn would further inspire multiuncertainties testing for continuum robot [9-14]. Fuzzy logic theory is used to estimate the system’s dynamics. To estimate the continuum robot manipulator’s dynamic of system, Mamdani fuzzy inference system is design and applied to inverse dynamic methodology [21-36].

Continuum robots represent a class of robots that have a biologically inspired form characterized by flexible backbones and high degrees-of-freedom structures [1]. The idea of creating “trunk and tentacle” robots, (in recent years termed continuum robots [1]), is not new [2]. Inspired by the bodies of animals such as snakes [3], the arms of octopi [4], and the trunks of elephants [5-6], researchers have been building prototypes for many years. A key motivation in this research has been to reproduce in robots some of the special qualities of the biological counterparts. This includes the ability to “slither” into tight and congested spaces, and (of particular interest in this work) the ability to grasp and manipulate a wide range of objects, via the use of “whole arm manipulation” i.e. wrapping their bodies around objects, conforming to their shape profiles. Hence, these robots have potential applications in whole arm grasping and manipulation in unstructured environments such as rescue operations. Theoretically, the compliant nature of a continuum robot provides infinite degrees of freedom to these devices. However, there is a limitation set by the practical inability to incorporate infinite actuators in the device. Most of these robots are consequently underactuated (in terms of numbers of independent actuators) with respect to their anticipated tasks. In other words they must achieve a wide range of configurations with relatively few control inputs. This is partly due to the desire to keep the body structures (which, unlike in conventional rigid-link manipulators or fingers, are required to directly contact the environment) “clean and soft”, but also to exploit the extra control authority available due to the continuum contact conditions with a minimum number of actuators. For example, the Octarm VI continuum manipulator, discussed frequently in this paper, has nine independent actuated degrees-of-freedom with only three sections. Continuum manipulators differ fundamentally from rigid-link and hyper-redundant robots by having an unconventional structure that lacks links and joints. Hence, standard techniques like the Denavit-Hartenberg (D-H) algorithm cannot be directly applied for developing continuum arm kinematics. Moreover, the design of each continuum arm varies with respect to the flexible backbone present in the system, the positioning, type and number of actuators. The constraints imposed by these factors make the set of reachable configurations and nature of movements unique to every continuum robot. This makes it difficult to formulate generalized kinematic or dynamic models for continuum robot hardware. Chirikjian and Burdick were the first to introduce a method for modeling the kinematics of a continuum structure by representing the curve-shaping function using modal functions [6]. Mochiyama used the Serret- Frenet formulae to develop kinematics of hyper-degrees of freedom continuum manipulators [5]. For details on the previously developed and more manipulator-specific kinematics of the Rice/Clemson “Elephant trunk” manipulator, see [15]. For the Air Octor and Octarm continuum robots, more general forward and inverse kinematics have been developed by incorporating the transformations of each section of the manipulator (using D-H parameters of an equivalent virtual rigid link robot) and expressing those in terms of the continuum manipulator section parameters [4]. The net result of the work in [3-6] is the establishment of a general set of kinematic algorithms for continuum robots. Thus, the kinematics (i.e. geometry based modeling) of a quite general set of prototypes of continuum manipulators has been developed and basic control strategies now exist based on these. The development of analytical models to analyze continuum arm dynamics (i.e. physicsbased models involving forces in addition to geometry) is an active, ongoing research topic in this field. From a practical perspective, the modeling approaches currently available in the literature prove to be very complicated and a dynamic model which could be conveniently implemented in an actual device’s realtime controller has not been developed yet. The absence of a computationally tractable dynamic model for these robots also prevents the study of interaction of external forces and the impact of collisions on these continuum structures. This impedes the study and ultimate usage of continuum robots in various practical applications like grasping and manipulation, where impulsive dynamics [1-4] are important factors. Although continuum robotics is an interesting subclass of robotics with promising applications for the future, from the current state of the literature, this field is still in its stages of inception.

This methodology is worked based on applied fuzzy logic in partly linear inverse dynamic plus gravity controller to estimate the equivalent nonlinear dynamic part. Pure inverse dynamic plus gravity controller has difficulty to calculate the best coefficient therefore gradient descent optimization (GDO) is used. The equivalent dynamic part of this controller is estimated depending on the last values of error (e) and change of error ( (̇ ) by gain updating factor (a) . Parallel fuzzy partly linear inverse dynamic controller is stable model-free controller which does not need to limits the dynamic model of continuum robot manipulator.

This paper is organized as follows; section 2, is served as an introduction to the inverse dynamic controller formulation algorithm and its application to control of continuum robot and dynamic of continuum robot, linear PD, PI, PID control and fuzzy logic techniques. Part 3, introduces and describes the methodology. Section 4 presents the simulation results and discussion of this algorithm applied to a continuum robot and the final section is describing the conclusion.

• II.    Theory

The Continuum section analytical model developed here consists of three modules stacked together in series. In general, the model will be a more precise replication of the behavior of a continuum arm with a greater of modules included in series. However, we will show that three modules effectively represent the dynamic behavior of the hardware, so more complex models are not motivated. Thus, the constant curvature bend exhibited by the section is incorporated inherently within the model. The model resulting from the application of Lagrange’s equations of motion obtained for this system can be represented in the form

^coeff X =(q) ̈+c(q) ̇+g(q ) (1)

where T is a vector of input forces and q is a vector of generalized co-ordinates. The force coefficient matrix ^coeff transforms the input forces to the generalized forces and torques in the system. The inertia matrix, D is composed of four block matrices. The block matrices that correspond to pure linear accelerations and pure angular accelerations in the system (on the top left and on the bottom right) are symmetric. The matrix C contains coefficients of the first order derivatives of the generalized co-ordinates. Since the system is nonlinear, many elements of c contain first order derivatives of the generalized co-ordinates. The remaining terms in the dynamic equations resulting from gravitational potential energies and spring energies are collected in the matrix G . The coefficient matrices of the dynamic equations are given below,

=

1	1	cos (01)	cos (01)	cos ( 9i + @2 )	COS ( 01 + 02 )
⎡0	0	1	1	cos (o2 )	COS ( 02 )	(2)
0	0	0	0	1	1
⎢1⁄2	-1⁄2	1⁄2	-1⁄2	1⁄2+ s2sm ( 02 )	-1⁄2 + s2sm ( 02 )
⎢0	0	1⁄2	-1⁄2	1⁄2	-1⁄2
⎣0	0	0	0	1⁄2	-1⁄2     ⎦

D(я)	⎡     nil + m2 + m3	m2cos (01) + m3cos (01)	m3cos (01 + 02)	- m2s2sin (01) - m3s2sin (01) - m3s3sin (01 + ^2)	- m3s3sin (01 + 02)	» ⎤	⎥⎥ ⎥
	m2cos (01) + m3cos (01)	m2 + m3	m3cos ( 6г )	- m3s3sin ( 02 )	- m3s3sin ( 02 )	0	⎥⎥
	m3cos (01 + ^2)	m3cos ( 02 )	m3	m3s3sin (02 )	0	0	⎥⎥                       (3)
	- m2s2sin (01) - m3s2sin (01) - m3s3sin (01 + ^2 )	- m3s3sin (02)	m3s2sin (02)	m2S2 + /1 + /2 + ^3 + m3S2 + m3s3 + 2m3s3cos ( ^2) ^2	^2 + m3s3 + /3 + m3s3cos (^2) S2		⎥⎥ ⎥⎥
	- m3s3sin (01 + ^2 )	- m3s3sin (02)	0	^2 + m3s3 + /3 + m3s3cos (02) $11	^2 + m3s3 + ^3	13	⎥ ⎥⎥
	⎣           0	0	0		^3	1, ⎦	⎥

с(1)=

с(я)=

Ch + C21	-2       (  ) ̇ -2       (  ) ̇	-2 m3sin ( 9i + ^2) ( 6 ̇ + 6 ̇ )	- m2s2 cos (01)( t ̇ ) +(1⁄2)(Си + C21) - m3s2 cos ( 9i )( t ̇ ) - m3s3 cos ( 01 + 02)( t ̇ )	- m3s3stn ( 9i + ^2 )	0⎤	⎥⎥ ⎥⎥
0	C12 + C22	-2 m3sin ( 02 ) ( 6 ̇ + 6 ̇ )	- т38з ( t ̇ ) +(1⁄2) (C12 + C2 2 ) -m3s2 ( t ̇ ) - m3s3 cos (02)( t ̇ )	-2 m3s3 cos ( 92 )( t ̇ ) - m3s3 cos ( 92 )( t ̇ )	0	⎥ ⎥                    (4)
0	2 m3sin (02)(6̇ )	C13 + C23	- m3s3s2 cos (02)( t ̇ ) - т38з ( t ̇ )	-2т3$з ( t ̇ ) - т353 ( t ̇ )	(1⁄2) (C13 + ^23)	⎥ ⎥⎥
(1⁄2) ( Сц + C21)	2m3s3 cos (02)( t ̇ ) -2 m3s2 ((̇ ) +2 TH2S2 ( f ̇ )	2 т35з (6̇+6̇) -2m3s2 cos ( 92) (6̇+6̇)	2 m3S3S2 sin (02)( t ̇ ) +(1 ⁄4) ( Сц + ^21)	m3s3s2 sin (02)( t ̇ )	0	⎥ ⎥⎥
0	(1⁄2)(C12 + C22)+ 2m3s3 cos (02)( t ̇ )	2 m3S3 (6̇+6̇)	т3$з$2 sin (02)( 6 ̇ )	(1 ⁄4) (C12 + ^22)	0	⎥⎥
0	0	(1⁄2)( C13 - C23 )	0	0	(1 ⁄4) (C13 + C23)⎦	⎥ ⎥

• ^-    т_гд - т₂д + ки ($1 + (1⁄2)61 - $01)+ к_и ($1-(1⁄2)61 - $01)-™зЯ

  - m₂gcos ( 61)+ к_г2 ( s₂ + (1⁄2) 9₂ - $02)+ к₂₂ ( s₂ - (1⁄2) 9₂ - $02)- m₃gcos ( 61 )

  - m₃gcos (01 + 6₂ )+ к« (s₃+(1⁄2)6₃ - $03)+ к₂з ( S3 -(1⁄2) 63 - S03 )

m₂s₂gsin (01)+m₃s₃ysin( Si + 02)+ m₃s₂gsin (01)+ ku ( Si + (1⁄2)Si - $01)(1⁄2) + k₂i ( Si -(1⁄2) 9i - Sol )(-1⁄2)

m₃s₃gsin (01 + 02)+ ki₂ ( s₂ +(1⁄2)02 - $02)(1⁄2) + k₂₂ ( S₂ -(1⁄2)02 - $02)(-1⁄2)

• -           ki3 ( S3 + (1⁄2) 63 - ■$03)(1⁄2) + k₂₃ ( S3 - (1⁄2) 63 - ■$03)(-1⁄2)

Linear PD, PI and PID Controller: In the absence of robot knowledge, proportional-integral-derivative (PID), proportional-integral (PI) and proportional -derivative (PD) may be the best controllers, because they are model-free, and they’re parameters can be adjusted easily and separately [1] and it is the most used in continuum robot manipulators. In order to remove steady-state error caused by uncertainties and noise, the integrator gain has to be increased. This leads to worse transient performance, even destroys the stability. The integrator in a PID controller also reduces the bandwidth of the closed-loop system. PD control guarantees stability only when the PD gains tend to infinity, the tracking error does not tend to zero when friction and gravity forces are included in the continuum robot manipulator dynamics [2]. Modelbased compensation for PD control is an alternative method to substitute PID control [1], such as adaptive gravity compensation [3], desired gravity compensation [2], and PD+ with position measurement [4]. They all needed structure information of the robot gravity. Some nonlinear PD controllers can also achieve asymptotic stability, for example PD control with time-varying gains [5], PD control with nonlinear gains [6], and PD control with feedback linearization compensation [8]. But these controllers are complex; many good properties of the linear PID control do not exist because these controllers do not have the same form as the industrial PID. Design of a linear methodology to control of continuum robot manipulator was very straight forward. Since there was an output from the torque model, this means that there would be two inputs into the PID controller. Similarly, the outputs of the controller result from the two control inputs of the torque signal. In a typical PID method, the controller corrects the error between the desired input value and the measured value. Since the actual position is the measured signal. Figure 1 is shown linear PID methodology, applied to continuum robot manipulator [9-16].

e(t) — aa(t) — ^(0

Up,_D = K_Pa e + K_Va e + K , ^e

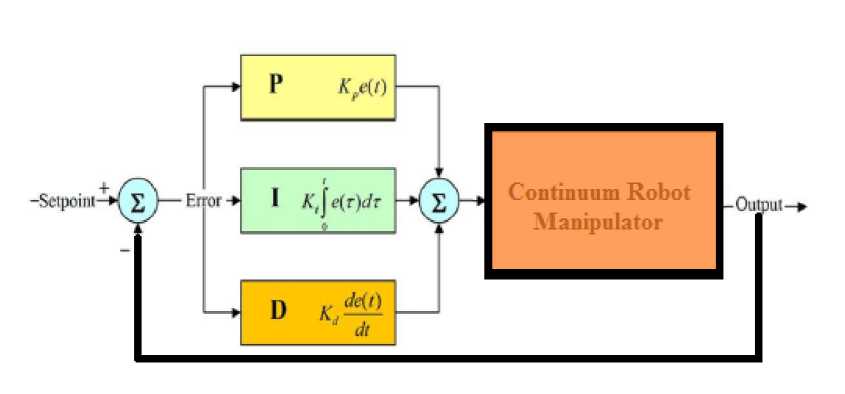
Fig. 1: Block diagram of linear PID method

The model-free control strategy is based on the assumption that the joints of the manipulators are all independent and the system can be decoupled into a group of single-axis control systems [14-16]. Therefore, the kinematic control method always results in a group of individual controllers, each for an active joint of the manipulator. With the independent joint assumption, no a priori knowledge of robot manipulator dynamics is needed in the kinematic controller design, so the complex computation of its dynamics can be avoided and the controller design can be greatly simplified. This is suitable for real-time control applications when powerful processors, which can execute complex algorithms rapidly, are not accessible. However, since joints coupling is neglected, control performance degrades as operating speed increases and a manipulator controlled in this way is only appropriate for relatively slow motion [13-16]. The fast motion requirement results in even higher dynamic coupling between the various robot joints, which cannot be compensated for by a standard robot controller such as PID [16], and hence model-based control becomes the alternative.

Inverse Dynamic Controller:

Inverse dynamic controller (IDC) is a powerful nonlinear controller which it widely used in control of robot manipulator. It is based on feedback linearization and computes the required arm torques using the nonlinear feedback control law. This controller works very well when all dynamic and physical parameters are known but when the robot manipulator has variation in dynamic parameters, in this situation the controller has not acceptable performance[14]. In practice, most of physical systems (e.g., robot manipulators) parameters are unknown or time variant, therefore, computed torque like controller used to compensate dynamic equation of robot manipulator[1, 6]. Research on IDC is significantly growing on robot manipulator application which has been reported in [1, 6, 15-16].Inverse dynamics control is based on cancelling decoupling and nonlinear terms of dynamics of each link. Inverse dynamics control has the form [6, 15 and 16]:

т — D(q). V + f(q)Vq 4] + C(q)lqp + G(q)

where typical choices for V are:

V — qd + Kv(qd - qa) + Kp(q d — q a)        (9)

or with an integral term

v —

where e — ( q^ — q _a), the resulting error dynamics is

Qd + Kve + Kp+ + Kj e — 0

where K_p , K_v and Kj are the controller gains. Based on (11) in inverse dynamic controller; the performance is depended on the gain updating factor (K): derivative gain updating factor (K_v), proportional gain updating factor (K_p) and integral gain updating factor (K₇).

Figure 2 shows the inverse dynamic methodology with application to continuum robot.

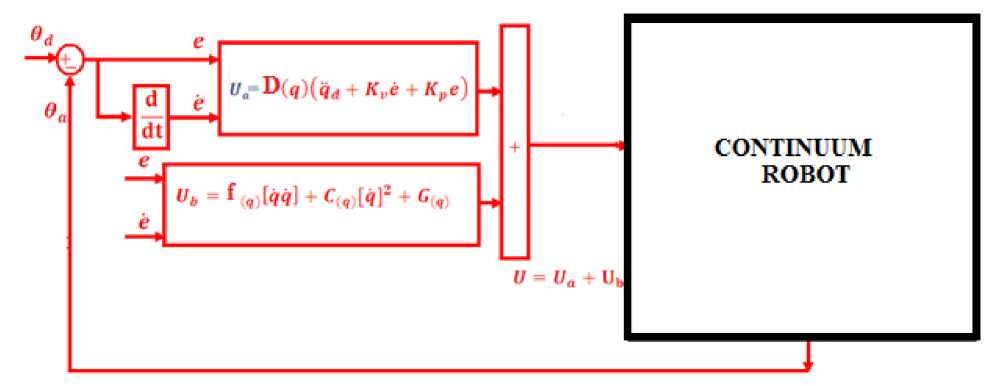
Fig. 2: Block diagram of inverse dynamic methodology

Fuzzy Logic Theory: This section provides a review about foundation of fuzzy logic based on [11-16]. Supposed that и is the universe of discourse and х is the element of U , therefore, a crisp set can be defined as a set which consists of different elements ( х ) will all or no membership in a set. A fuzzy set is a set that each element has a membership grade, therefore it can be written by the following definition;

л ={х, На (х)|х∈X}; А∈U (12)

Where an element of universe of discourse is X , (Лд is the membership function (MF) of fuzzy set. The membership function ( (Лд ( X )) of fuzzy set Д must have a value between zero and one. If the membership function (Лд ( X ) value equal to zero or one, this set change to a crisp set but if it has a value between zero and one, it is a fuzzy set. Defining membership function for fuzzy sets has divided into two main groups; namely; numerical and functional method, which in numerical method each number has different degrees of membership function and functional method used standard functions in fuzzy sets. The membership function which is often used in practical applications includes triangular form, trapezoidal form, bell-shaped form, and Gaussian form.

Linguistic variable can open a wide area to use of fuzzy logic theory in many applications (e.g., control and system identification). In a natural artificial language all numbers replaced by words or sentences.

If - t ℎ en Rule statements are used to formulate the condition statements in fuzzy logic. A single fuzzy If - t ℎ еп rule can be written by

If х is A Then у is В (13)

where д and в are the Linguistic values that can be defined by fuzzy set, the If - part of the part of “х is A ” is called the antecedent part and the t ℎ en - part of the part of “у is В ” is called the Consequent or

Conclusion part. The antecedent of a fuzzy if-then rule can have multiple parts, which the following rules shows the multiple antecedent rules:

if e is NB and t ̇ is ML then T is LL (14)

where e is error, c ̇ is change of error, NB is Negative Big, ML is Medium Left, T is torque and LL is Large Left. If - t ℎ en rules have three parts, namely, fuzzify inputs, apply fuzzy operator and apply implication method which in fuzzify inputs the fuzzy statements in the antecedent replaced by the degree of membership, apply fuzzy operator used when the antecedent has multiple parts and replaced by single number between 0 to 1, this part is a degree of support for the fuzzy rule, and apply implication method used in consequent of fuzzy rule to replaced by the degree of membership. The fuzzy inference engine offers a mechanism for transferring the rule base in fuzzy set which it is divided into two most important methods, namely, Mamdani method and Sugeno method. Mamdani method is one of the common fuzzy inference systems and he designed one of the first fuzzy controllers to control of system engine. Mamdani’s fuzzy inference system is divided into four major steps: fuzzification, rule evaluation, aggregation of the rule outputs and defuzzification. Michio Sugeno uses a singleton as a membership function of the rule consequent part. The following definition shows the Mamdani and Sugeno fuzzy rule base

Mamdani F . R¹ :

у is В then z is C Sugeno   F . R¹ :

у is В then     f ( x , У ) is C

When X and у have crisp values fuzzification calculates the membership degrees for antecedent part. Rule evaluation focuses on fuzzy operation (AND /OR ) in the antecedent of the fuzzy rules. The aggregation is used to calculate the output fuzzy set and several methodologies can be used in fuzzy logic controller aggregation, namely, Max-Min aggregation, Sum-Min aggregation, Max-bounded product, Max-drastic product, Max-bounded sum, Max-algebraic sum and Min-max. Two most common methods that used in fuzzy logic controllers are Max-min aggregation and Sum-min aggregation. Max-min aggregation defined as below

Д и ⁽Хk,Уk,U) = Д ц^я ^Х _к, у к. и)

= mах, min[= к [дй pq(Хк,Ук),ДРт(Ю]}

The Sum-min aggregation defined as below

Д и ⁽Хк,Ук,Ю = M uUFB «Хк.Ук.Ю

= ^ min[= ! [ддPq(Хк,у к), ДРт(Ю]

where г is the number of fuzzy rules activated by x_k and y_k and also д_и г _FRt(x_k,y_k, U) is a fuzzy interpretation of - — th rule. Defuzzification is the last step in the fuzzy inference system which it is used to transform fuzzy set to crisp set. Consequently defuzzification’s input is the aggregate output and the defuzzification’s output is a crisp number. Centre of gravity method ( C0 G) and Centre of area method ( C0A) are two most common defuzzification methods, which C0 G method used the following equation to calculate the defuzzification

С О G (Хк,у к)

TdUtT^ ,. ^(Хк, Ук, Ud ВД=1. Ди(Х_к, Ук, U_t)

and       method used the following equation to calculate the defuzzification

^X i Ui- ^Ди^(Хк,^у к, U^

^{С0Д(Хк,Ук)=} T_lДu.(Х k ,У_t,U_l)           ⁽1⁹⁾

Where COG(x_fc,y_fc) and COA(x_k,y_k) illustrates the crisp value of defuzzification output, U / £ U is discrete element of an output of the fuzzy set, ц_и. (x_k,y_k, U / ) is the fuzzy set membership function, and r is the number of fuzzy rules.

Based on foundation of fuzzy logic methodology; fuzzy logic controller has played important rule to design nonlinear controller for nonlinear and uncertain systems [12-16]. However the application area for fuzzy control is really wide, the basic form for all command types of controllers consists of:

• •    Input fuzzification (binary-to-fuzzy[B/F]conversion)

• •    Fuzzy rule base (knowledge base)

• •    Inference engine

• •    Output   defuzzification   (fuzzy-to-binary [F/B]

conversion).

Figure 3 shows the block digram of fuzzy logic control methodology based on two inputs and one output.

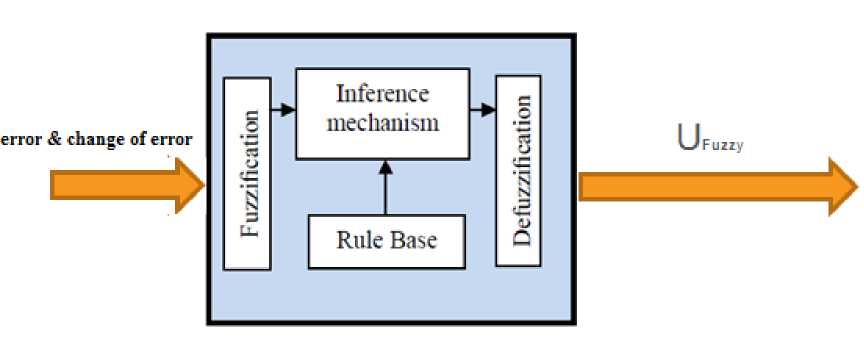
Fig. 3: Block diagram of fuzzy logic control methodology

• III.    Methodology

Inverse dynamic controller (IDC) is an important nonlinear controller in a partly uncertain dynamic system’s parameters. This controller is used in several applications such as in robotics, process control, aerospace and power electronics. Inverse dynamic controller is used to control of nonlinear dynamic systems particularly for continuum robot manipulators, because it has a suitable control performance and it is a robust and stable. Conversely pure IDC is a high-quality nonlinear controller; it has an important problem; nonlinear equivalent dynamic formulation in uncertain dynamic parameter. In this research the nonlinear equivalent dynamic (equivalent part) formulation problem in uncertain system is estimated by using fuzzy logic theorem. Fuzzy logic theory is used to estimate of the equivalent part in fuzzy partly linear inverse dynamic controller. In this method fuzzy logic theorem is parallel applied to inverse dynamic controller to remove the nonlinear equivalent part which it is based on nonlinear dynamic formulation. To achieve this goal, the dynamic equivalent part of pure inverse dynamic controller is modeled by Mamdani’s performance/ error-based fuzzy logic methodology. This technique was employed to obtain the desired control behavior with a number of information about dynamic model of system and a parallel fuzzy control was applied to reinforce system performance. As shown in Figure 3, IDC is divided into two main parts: partly linear part and equivalent part. Partly linear part is work based on design linear controller (PD, PI and/or PID) and applied to inertial matrix. Equivalent part is based on continuum robot manipulator’s dynamic formulation which these formulations are nonlinear; MIMO and some of them are unknown. To solve the challenge of IDC based on nonlinear dynamic formulation this research is focused on eliminate the nonlinear equivalent formulation. In this method; dynamic nonlinear equivalent part is replaced by performance/error-based fuzzy logic controller plus gravity term. In fuzzy parallel error-based inverse dynamic controller plus gravity; error based Mamdani’s fuzzy inference system has considered with two inputs, one output and totally 49 rules instead of the dynamic equivalent part. Figure 4 shows error-based parallel fuzzy inverse dynamic controller plus gravity.

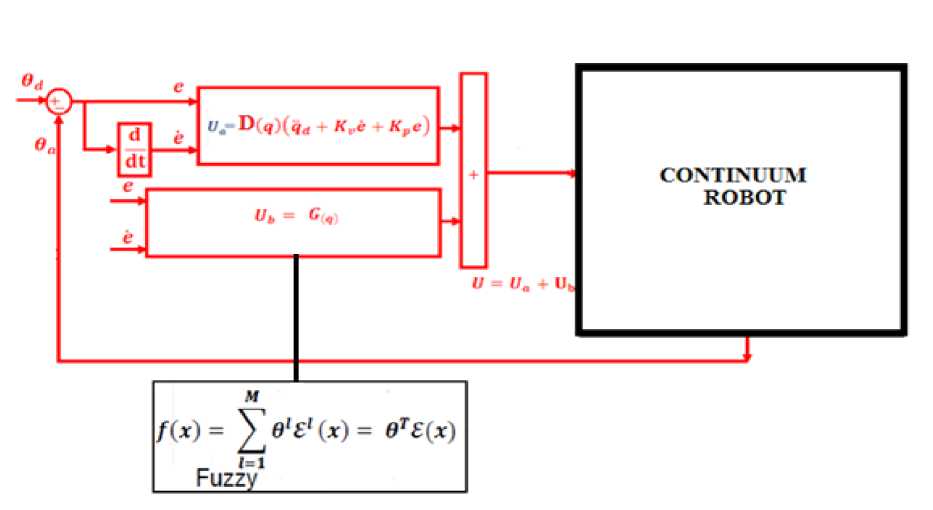
Fig. 4: Block diagram of parallel fuzzy logic inverse dynamic control plus gravity methodology

For inverse dynamic controller and parallel fuzzy inverse dynamic controller plus gravity applications the system performance is sensitive to the linear PD coefficient (K_p &  К). . For instance, if large value of K_p & K_v are chosen the response is very fast the system is unstable and conversely, if small value of K_p & K_v are considered the response of system is very slow but system is stable. Therefore to have a good response, compute the best value linear coefficients are very important. Figure 4 has three main parts: partly linear part, gravity part and parallel Mamdani error-based fuzzy part. Based on Figure 5, the parallel fuzzy errorbased inverse dynamic controller’s output is written;

T = t eqfuzzy + TPartly Hnear + G( q)

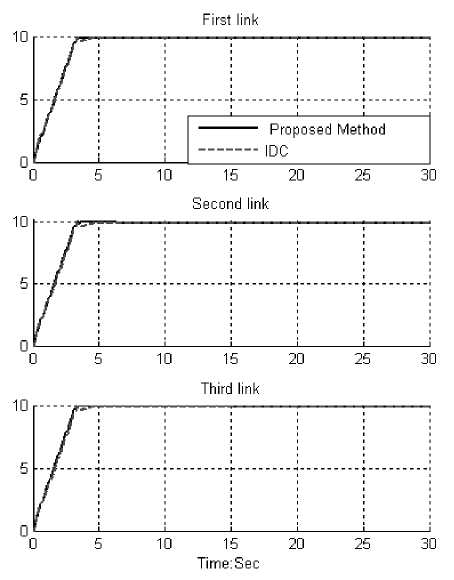
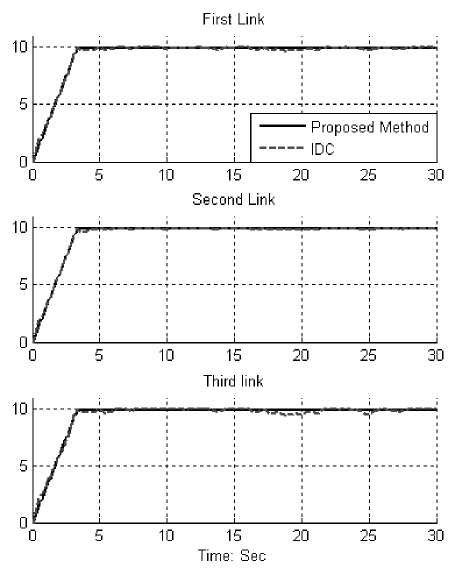
Based on fuzzy logic methodology f (x) — U f„zzy-Z^ i0r

< *-^

т№ - E* 1 eT <(x) - [(f + O](23)

• IV.    Result and Discussion

Robust parallel Mamdani fuzzy estimator IDC controller plus gravity (proposed method) was tested to ramp response trajectory. The simulation was implemented in MATLAB/SIMULINK environment.

Tracking performances: Figure 5 shows tracking performance for proposed method and inverse dynamic controller (IDC) without disturbance.

Fig. 5: proposed method and IDC for three joints trajectory

Fig. 6: Proposed method and IDC for three joints trajectory with disturbance

Disturbance rejection: Figure 6 shows the power disturbance elimination in IDC and proposed method. The main target in this controller is disturbance rejection as well as the other responses. A band limited white noise with predefined of 40% the power of input signal is applied to IDC and proposed method. It found fairly fluctuations in IDC responses. As mentioned earlier, IDC works very well when all parameters are known, or we have a limitation uncertainty in parameters.

• V.    Conclusion

One of the most active research areas in field of continuum robot is artificial nonlinear control of this system because this system is a nonlinear, time variant and uncertain system. To control of this system robust inverse dynamic methodology is introduced. Inverse dynamic controller (IDC) is an influential robust nonlinear controller to certain and partly uncertain systems. When all dynamic and physical parameters are known IDC works superbly; practically a large amount of systems have uncertainties and Mamdani parallel fuzzy inference optimization add to inverse dynamic plus gravity controller. Based on above discussion this method has acceptable performance against to pure inverse dynamic controller in presence of uncertainty.

Acknowledgment

The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments. This work was supported by the SSP Research and Development Corporation Program of Iran under grant no. 2013-Persian Gulf-2B.