Design PID Baseline Fuzzy Tuning Proportional- Derivative Coefficient Nonlinear Controller with Application to Continuum Robot

The flexible manipulator started to play an important part in many engineering applications nowadays. Major advantages of flexible manipulators include small mass, fast motion, and large force to mass ratio, which are reflected directly in the reduced energy consumption, increased productivity, and enhanced payload capacity. Unlike the rigid manipulators, the difficulties facing the usage of flexible manipulators are numerous. The modeling of the flexibility of the manipulator is one of the challenges, the non-minimum phase problem, which appears from the modeling of the flexible manipulators, is also another challenge. The precise and availability of the measured variables used in the control is the third challenge. The control of flexible manipulators has been studied with great interest by many researchers over the past years due to its pronounced benefits. To find a controller that can achieve the end effector position of the flexible manipulator in a short time in addition to a suppression of its vibration to be able to achieve the tasks is the main goal of the control of flexible manipulator in the free space. Although significant progresses have been made in many aspects over the last two decades, many issues are not yet resolved yet, and simple, effective, and reliable controls of flexible manipulators remain open requests [1-15].

There are several methods for controlling a flexible robot manipulator, which all of them follow important main goals, namely, acceptable performance [16-21]. However, the mechanical design of flexible robot manipulator is very important to select the best controller to have a reduce vibration but in general two types schemes can be presented, namely, a joint space control schemes and an operation space control schemes[13-23]. Controller is a device which can sense information from linear or nonlinear system (e.g., robot manipulator) to improve the systems performance [2022]. The main targets in design a control systems are stability, good disturbance rejection, and small tracking error[5, 23-40]. Several robot manipulators are controlled by linear methodologies (e.g., Proportional-Derivative (PD) controller, Proportional- Integral (PI) controller or Proportional- Integral-Derivative (PID) controller), but when Robot manipulator works in various situation and have uncertainty in dynamic models this technique has limitations. Strong mathematical tools used in new control methodologies to design nonlinear robust controller with an acceptable performance (e.g., minimum error, good trajectory, disturbance rejection). There have been several robot controller designs over the past 40 years in which the goal is to improve the efficiency and reduce the error of the robot manipulator. Computed torque controller (CTC) is a powerful nonlinear controller which it widely used in control of continuum robot manipulator. It is based on feedback linearization and computes the required arm torques by the nonlinear feedback control law. This controller works very well when all dynamic and physical parameters are known but when the system has variation in dynamic parameters, the controller has no acceptable performance[14]. In practice, most of physical systems (e.g., continuum robot manipulators)

parameters are unknown or time variant, therefore, computed torque like controller used to compensate dynamic equation of robot manipulator[15-23]. When all dynamic and physical parameters are known, computed torque controller works fantastically; practically a large amount of systems have uncertainties, therefore fuzzy inference methodology is one of the best case to solve this challenge. In recent years, artificial intelligence theory has been used in nonlinear controllers. Neural network, fuzzy logic and neuro-fuzzy are synergically combined with nonlinear classical controller and used in nonlinear, time variant and uncertain plant (e.g., continuum robot manipulator). Fuzzy logic controller (FLC) is one of the most important applications of fuzzy logic theory. This controller can be used to control nonlinear, uncertain, and noisy systems. This method is free of some model techniques as in model-based controllers. As mentioned that fuzzy logic application is not only limited to the modelling of nonlinear systems [31-36] but also this method can help engineers to design a model-free controller.

Model based control robot manipulators is based on manipulator dynamic model. These controllers often have many problems for modelling. Conventional controllers require accurate information of dynamic model of continuum robot manipulator, but most of time these models are MIMO, nonlinear and partly uncertain parameters therefore calculate accurate dynamic model is complicated [30-45]. The main reasons to use fuzzy logic methodology are able to give approximate recommended solution for uncertain and also certain complicated systems to easy understanding and flexible. Fuzzy logic provides a method to design a model-free controller for nonlinear plant with a set of IF-THEN rules [46-55].

This research focuses on the design modified baseline computed torque controller (BLCTC) based on fuzzy logic optimization theory. This methodology is based on design PID controller and applied to modified PD methodology and applied to computed torque controller and optimized the coefficients by fuzzy logic theory. This paper is organized as follows: Detail of linear PID controller, classical computed torque controller, fuzzy inference engine and dynamic formulation of flexible continuum robot manipulator are presented in section 2, theory. In section 3, methodology, the main subject of design supervised fuzzy modified baseline computed torque controller is presented. In section 4, the simulation result is presented and finally in section 5, the conclusion is presented.

• II.    Theory

Dynamic Modeling of Continuum Robot: The Continuum section analytical model developed here consists of three modules stacked together in series. In general, the model will be a more precise replication of the behavior of a continuum arm with a greater of modules included in series. However, we will show that three modules effectively represent the dynamic behavior of the hardware, so more complex models are not motivated. Thus, the constant curvature bend exhibited by the section is incorporated inherently within the model. The model resulting from the application of Lagrange’s equations of motion obtained for this system can be represented in the form

^coeff 1 = . q / ̈ + c . q / ̇ + g . q / (1)

where T is a vector of input forces and q is a vector of generalized co-ordinates. The force coefficient matrix ^coeff transforms the input forces to the generalized forces and torques in the system. The inertia matrix, D is composed of four block matrices. The block matrices that correspond to pure linear accelerations and pure angular accelerations in the system (on the top left and on the bottom right) are symmetric. The matrix c contains coefficients of the first order derivatives of the generalized co-ordinates. Since the system is nonlinear, many elements of c contain first order derivatives of the generalized co-ordinates. The remaining terms in the dynamic equations resulting from gravitational potential energies and spring energies are collected in the matrix G . The coefficient matrices of the dynamic equations are given below,

=

( 01 )      ( 01 )        ( 01 + o₂ )          ( 01 + o₂ )

⎢ 0     0       1         1          cos(o2)(

⎢0  0   0    0      111

^⎢ ⁄2   - ⁄2   1⁄2      - ⁄2   1⁄2 + s^sin ( 0₂ ) - ⁄2 + s^sin ( 0₂ )

⎢0     0     1⁄2     - ⁄2         1⁄2              - ⁄2I

⎣0     0       0        0           1⁄2              - ⁄2⎦

° .я/=

⎡         + +	m2cos(6i) +       (6i)	( 6i + 62 )	-         (6i) -         ( 6i ) -        (6i + 62)	-         (6i + 62 )    ⎤ ⎥⎥
⎢     m2cos (6i) ⎢+ macos (6i)	+	m3cos(6?)	-m3s3sin(6? )	⎥ -m3s3sin(62)
m3cos(6i + 6?)	m3cos(6?)	m3	m3s3sin(6?)	⎥⎥
⎢-m2s2sin(6i) -m3s2sin(6i) -m3s3sin(6i + 6? )	-          (6?)	m3s2sin(6?)	+  + +  +     + +         (6?)	⎥⎥ +       +               ⎥ +m3s3cos(62 )       ⎥
⎢ -m3s3sin(  +  )	-          (6?)	о	+    + +m3s3cos(6?)	⎥ +       +               ⎥
⎣	o	o		⎦

c . ⎢⎢⎢⎢⎢⎢                 +	я/= -         (61) ̇ -2m3sin(6i) ̇	-       ( 6i + 62 ) ( ̇+ ̇)	- (6i)( ̇ ) +(⁄)(  +  ) - ( 6i)( ̇ ) - (6i + 62)( ̇ )	-        (61 + 62)	⎤	⎥⎥⎥⎥⎥⎥
⎢⎢⎢⎢⎢⎢⎢	+	-        (62) ( ̇+ ̇)	-      ( ̇ ) +(⁄) (   +   ) -      ( ̇ ) - (62)( ̇ )	- (62)( ̇ ) - (62)( ̇ )	о	⎥⎥⎥        (4)
⎢⎢⎢	2m3sin(62)( ̇ )	+	- (62)( ̇ ) -      ( ̇ )	-        ( ̇ ) -      ( ̇ )	(1⁄2) (   +   )	⎥⎥⎥⎥
⎢⎢ ( ! ⁄2)     2m3s3cos ( »■)( ̇ ) ⎢(     +     )        -         ( ̇ ) ⎢⎢                              +           ( )		( ̇ +  ̇ ) -          (62) ( ̇+  ̇)	2m3s3s2 (62)( ̇ ) +( ⁄ ) ( + )	(62 )( ̇ )	о	⎥⎥⎥⎥⎥⎥
⎢⎢⎢	(⁄)(  +  )+ 2m3s3cos(62)( ̇ )	( ̇+ ̇)	(62)( ̇ )	(  ⁄ ) (   +   )	о	⎥⎥⎥
⎢ ⎣	0	(⁄)(  -  )	0	0	(  ⁄ ) (    +    )⎦	⎥⎥

G (,) =

—m 1g — m₂ g + к _г 1 ⁽ s 1 + (1/2)0 _г — s 01 ) + к ₂ 1 ⁽ s _г — ⁽l^/2)0 _г — s 01 ) — m ₃ g

—m₂gcos⁽0 1 ) + ki2⁽s₂ + ⁽1^/2)0₂ — S 02 ) + k₂₂⁽s₂ — ⁽1^/2)0₂ — S 02 ) — m 3 gcos⁽0 i )

—m 3 gcos⁽0₁ + 0₂) + k i3 ⁽S 3 + ⁽1^/2⁾0 з — s₀ 3 ) + k₂ 3 ⁽S 3 — ⁽1^/2⁾0 з — s₀ 3 )

m₂s₂gsin(0 i ) + m 3 S 3 gsin(0_t + 0₂) + m 3 s₂gsin(0₁) + k₁₁(s₁ + (1/2)0 1 — s₀₁)(1/2) +k₂₁(s₁ —(1/2)0 ! —s₀₁)(—1/2)

m 3 S 3 gsin⁽0 1 + 0₂) + k t ₂⁽s₂ + ⁽l^/2)0₂ — S02KV2) + k₂₂⁽s₂ — ⁽V2)0₂ — s o ₂⁾⁽—1^/2⁾

k 13 (s 3 + (1/2)0 3 — S 03 )(1/2) + k₂ 3 (s 3 — (1/2)0 3 — So₃)(—1/2)

Design PID Controller: Design of a linear methodology to control of flexible robot manipulator was very straight forward. Since there was an output from the torque model, this means that there would be two inputs into the PID controller. Similarly, the outputs of the controller result from the two control inputs of the torque signal. In a typical PID method, the controller corrects the error between the desired input value and the measured value. Since the actual position is the measured signal. Figure 1 is shown linear PID methodology, applied to flexible robot manipulator [2634].

e (t) = 0_a(t) — 0_d(t)

WP/D = ^Pae + ^Kae + ^/^e

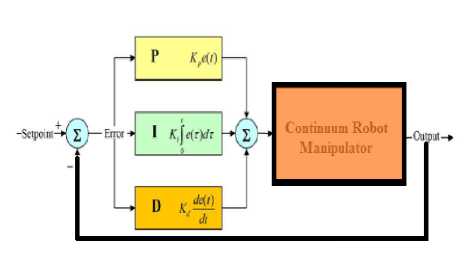
Fig. 1: Block diagram of linear PID method

The model-free control strategy is based on the assumption that the joints of the manipulators are all independent and the system can be decoupled into a group of single-axis control systems [18-23]. Therefore, the kinematic control method always results in a group of individual controllers, each for an active joint of the manipulator. With the independent joint assumption, no a priori knowledge of robot manipulator dynamics is needed in the kinematic controller design, so the complex computation of its dynamics can be avoided and the controller design can be greatly simplified. This is suitable for real-time control applications when powerful processors, which can execute complex algorithms rapidly, are not accessible. However, since joints coupling is neglected, control performance degrades as operating speed increases and a manipulator controlled in this way is only appropriate for relatively slow motion [34-37]. The fast motion requirement results in even higher dynamic coupling between the various robot joints, which cannot be compensated for by a standard robot controller such as PID [36], and hence model-based control becomes the alternative.

Computed Torque Controller: The central idea of Computed torque controller (CTC) is feedback linearization method therefore, originally this algorithm is called feedback linearization controller. It has assumed that the desired motion trajectory for the manipulator q ^ (t), as determined, by a path planner. Defines the tracking error as [23-37]:

e ⁽t ) = q_d ⁽t ) — q_a(t) (8)

Where e(t) is error of the plant, q ^ (t) is desired input variable, that in our system is desired displacement, q_a(t) is actual displacement. If an alternative linear state-space equation in the form x = Лх + BU can be defined as

^G Дх+[®1и

With U = —D^-1(q).N(q,q) + D^-1(q).T and this is known as the Brunousky canonical form. By equation (8) and (9) the Brunousky canonical form can be written in terms of the state x = [e^r e^T]^T as [11-34]:

^o:i=g ;i-o:i+[?iu

With

U = qd + D-1(q).{N(q.q)—T}

Then compute the required arm torques using inverse of equation (11), is;

T = D(q)(q4 — U) + N(q,q)(12)

This is a nonlinear feedback control law that guarantees tracking of desired trajectory. Selecting proportional-plus-derivative (PD) feedback for U(t) results in the PD-computed torque controller [8-10];

T = D(q)(q_d + K_ve^ + K_pe) + ^(q,qf)         ⁽¹³⁾

Where N(q, q") is nonlinear term of system dynamic;

^(q,q) = 7 (q) [qq] + C (q) [q]² + G₍ q)            (14)

According to the linear system theory, convergence of the tracking error to zero is guaranteed [6]. Where K_p and K_p are the controller gains.

Fuzzy Inference Engine: This section provides a review about foundation of fuzzy logic based on [3236]. Supposed that U is the universe of discourse and x is the element of U, therefore, a crisp set can be defined as a set which consists of different elements (x) will all or no membership in a set. A fuzzy set is a set that each element has a membership grade, therefore it can be written by the following definition;

л ={ х , На ( х )| х ∈ X }; А ∈ U (15)

Where an element of universe of discourse is X , {Лд is the membership function (MF) of fuzzy set. The membership function ( Ца ( X )) of fuzzy set А must have a value between zero and one. If the membership function {Л А ( X ) value equal to zero or one, this set change to a crisp set but if it has a value between zero and one, it is a fuzzy set. Defining membership function for fuzzy sets has divided into two main groups; namely; numerical and functional method, which in numerical method each number has different degrees of membership function and functional method used standard functions in fuzzy sets. The membership function which is often used in practical applications includes triangular form, trapezoidal form, bell-shaped form, and Gaussian form.

Linguistic variable can open a wide area to use of fuzzy logic theory in many applications (e.g., control and system identification). In a natural artificial language all numbers replaced by words or sentences.

If - t ℎ en Rule statements are used to formulate the condition statements in fuzzy logic. A single fuzzy If - t ℎ еп rule can be written by

If х is A Then у is В (16)

where A and В are the Linguistic values that can be defined by fuzzy set, the If - part of the part of “x is A ” is called the antecedent part and the t ℎ en - part of the part of “у is В ” is called the Consequent or Conclusion part. The antecedent of a fuzzy if-then rule can have multiple parts, which the following rules shows the multiple antecedent rules:

if e is NB and t ̇ is ML then T is LL (17)

where e is error, ̇ is change of error, NB is Negative Big, ML is Medium Left, T is torque and LL is Large Left. If -tℎen rules have three parts, namely, fuzzify inputs, apply fuzzy operator and apply implication method which in fuzzify inputs the fuzzy statements in the antecedent replaced by the degree of membership, apply fuzzy operator used when the antecedent has multiple parts and replaced by single number between 0 to 1, this part is a degree of support for the fuzzy rule, and apply implication method used in consequent of fuzzy rule to replaced by the degree of membership. The fuzzy inference engine offers a mechanism for transferring the rule base in fuzzy set which it is divided into two most important methods, namely, Mamdani method and Sugeno method. Mamdani method is one of the common fuzzy inference systems and he designed one of the first fuzzy controllers to control of system engine. Mamdani’s fuzzy inference system is divided into four major steps: fuzzification, rule evaluation, aggregation of the rule outputs and defuzzification. Michio Sugeno use a singleton as a membership function of the rule consequent part. The following definition shows the Mamdani and Sugeno fuzzy rule base

Mamdani F ․ R¹ :

у is В then z is C Sugeno   F ․ R¹ :

у is В then     f ( x , У ) is C

When X and    have crisp values fuzzification calculates the membership degrees for antecedent part. Rule evaluation focuses on fuzzy operation (AND /OR ) in the antecedent of the fuzzy rules. The aggregation is used to calculate the output fuzzy set and several methodologies can be used in fuzzy logic controller aggregation, namely, Max-Min aggregation, Sum-Min aggregation, Max-bounded product, Max-drastic product, Max-bounded sum, Max-algebraic sum and Min-max. Two most common methods that used in fuzzy logic controllers are Max-min aggregation and Sum-min aggregation. Max-min aggregation defined as below

Bu ⁽ x_k , Ук , и )= В ⋃ ^Ti=l^{FRi (} x_k , Ук , и ⁾ =     2min[₌₁ 0 hRpq ⁽ Xk , Ук ), Bp_m ⁽ и )13

The Sum-min aggregation defined as below

Bu ( x_k , Ук , и )= в ⋃ Ll^FRi ( x_k , Ук , и ) =∑minr₌₁ 0 h^Rpq ( Xk , Ук ), h^Pm ( U )1

where r is the number of fuzzy rules activated by Xr and Ук and also fl u l=l^FRi ( Xk , Ук , u ) is a fuzzy interpretation of i - t ℎ rule. Defuzzification is the last step in the fuzzy inference system which it is used to transform fuzzy set to crisp set. Consequently defuzzification’s input is the aggregate output and the defuzzification’s output is a crisp number. Centre of gravity method ( COG ) and Centre of area method ( COA ) are two most common defuzzification methods, which COG method used the following equation to calculate the defuzzification

COG ( x_k , Ук )

^∑ _tU_t ^∑ ^=1 ․ Bu ( Xk , Ук , Ui ) ∑∑ ^=1 ․ Bu ( x_k , Ук , Ui )

and COA method used the following equation to calculate the defuzzification

COA ( x_k , Ук )

^∑ jUt ․ Bu ( Xk , Ук , Hl ) ^∑ iBu ․( Xk , Ук , Ui )

Where COG(xk , Ук ) and COA ( xk , Ук ) illustrates the crisp value of defuzzification output, U[ ∈и is discrete element of an output of the fuzzy set, цu. (х^у^, V/) is the fuzzy set membership function, and r is the number of fuzzy rules.

Based on foundation of fuzzy logic methodology; fuzzy logic controller has played important rule to design nonlinear controller for nonlinear and uncertain systems [30-37]. However the application area for fuzzy control is really wide, the basic form for all command types of controllers consists of;

• •    Input fuzzification (binary-to-fuzzy[B/F]conversion)

• •    Fuzzy rule base (knowledge base)

• •    Inference engine

• •    Output           defuzzification           (fuzzy-to-

• binary[F/B]conversion).

Figure 2 shows the part in fuzzy logic theory.\

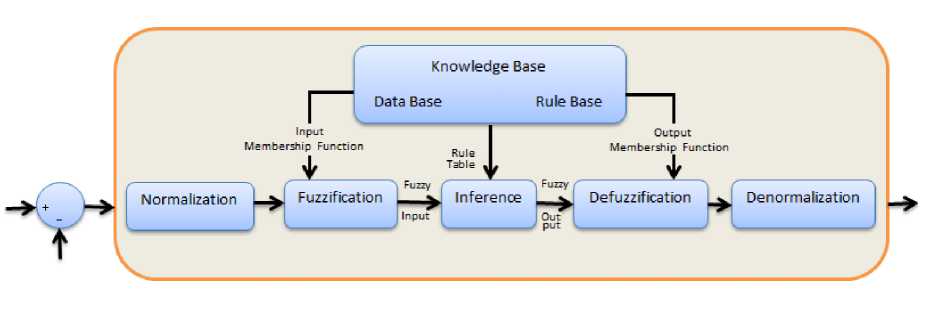
Fig. 2: Block diagram of Fuzzy Logic Control

• III.    Methodology

Design of a baseline nonlinear model-free methodology to control the continuum robot manipulator was very straight forward. The first part of baseline controller is linear PID controller. This controller has three coefficients, namely: K_p, K_v , and К/ . These play important role to tune the first part of controller. The second block of baseline methodology in this research is linear PD controller. This controller is connected to the previous block based on the serial connected. This controller has one coefficient, namely: .

e(t) - 0_d0) - a_a0)                       (23)

U _P1D - K_pe + К e +K^e            ⁽²⁴⁾

UBASEL INE ^- C^ U p_1D ⁺  ₊ у ^X Upi в )

Figure 3 shows the baseline methodology application in this research.

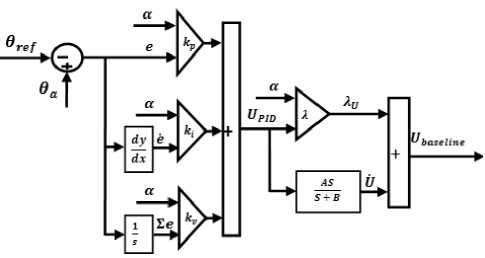
Fig. 3: Block diagram of Baseline Methodology

According to the pure computed torque controller (13) and baseline methodology (25);

Tnew-etc - O⁽q⁾⁽ q_d + и в ASE LIN E ) ⁺         (26)

N ⁽ q, q)

However both controllers (baseline and computed torque controller) have been used in control robot manipulator, but design modified baseline computed torque controller strategy gives better result as a performance. Figure 4 shows the baseline computed torque controller with application to continuum robot manipulator.

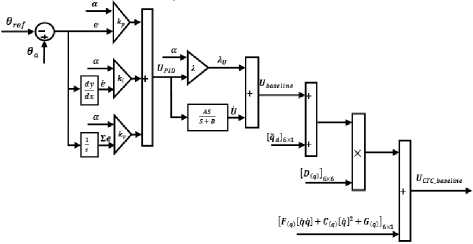
Fig. 4: Block diagram of Baseline Computed Torque Methodology

When all dynamic and physical parameters are known, baseline CTC works fantastically. This is a nonlinear feedback control law that guarantees tracking of continuum robot trajectory. According to the linear system theory, convergence of the tracking error to zero is guaranteed. According to the pure computed torque controller and pure baseline controller, Baseline computed torque controller has difficulty in handling unstructured model uncertainties. It is possible to solve this problem by combining proposed controller (BLCTC) and fuzzy-based tuning method which this method can helps to reduce the error in presence of model base controller and improves the system’s tracking performance by online tuning method. Based on above discussion, compute the best value of controller coefficient has played important role to improve system’s tracking performance especially when the system parameters are unknown or uncertain. This problem is solved by tuning the baseline coefficients continuously in real-time. In this methodology, the system’s performance is improved with respect to the classical computed torque controller and baseline computed torque controller.

̂( |  ) as the fuzzy based tuning.

^̂( X | К )= К¹^ ( х )                             (27)

If minimum error ( К ^∗) is defined by;

к ∗₌ arg mtn [. Sup | ̂( х | К )- f ( х )/]        (28)

where к^т is adjusted by an adaption law and this law is designed to minimize the error’s parameters of к - к ^∗․ adaption law in fuzzy-based tuning BLCTC is used to adjust the controller coefficients. Fuzzy-based tuning part is a supervisory controller based on Mamdani’s fuzzy logic methodology. This controller has two inputs namely; error ( е ) and change of error ( е ̇) and an output namely; gain updating factor ( а ) . As a summary design a fuzzy-based tuning based on fuzzy logic method in fuzzy based tuning BLCTC has five steps:

• 1.    Determine inputs and outputs : it has two inputs error and change of error ( е , €̇) and the output name’s is controller coefficient updating factor ( а ).

• 2.    Find linguistic variable : The linguistic variables for error(e) are; Negative Big (NB), Negative Medium (NM), Negative Small (NS), Zero (Z), Positive Small (PS), Positive Medium (PM), Positive Big (PB), and it is quantized into thirteen levels represented by: -1, -0.83, -0.66, -0.5, -0.33, -0.16, 0, 0.16, 0.33, 0.5, 0.66, 0.83, 1, the linguistic variables for change of error( е ̇) are ;Fast Left (FL), Medium Left (ML), Slow Left (SL),Zero (Z), Slow Right (SR), Medium Right (MR), Fast Right (FR), and it is quantized in to thirteen levels represented by: -6, -5, -0.4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, and the linguistic variables for controller coefficient updating factor ( а ) are; Zero (ZE), Very Small (VS), Small (S), Small Big (SB), Medium Big (MB), Big (B), and Very Big (VB) and they are defined on [0․5,1] and quantized into thirteen levels respected by: 0.5, 0.5417, 0.583, 0.625, 0.667, 0.7087, 0.7503, 0.792, 0.834, 0.876, 0.917, 0.959, 1.

• 3.    Type of membership function : In this research triangular membership function is selected because it

• 4.    Design fuzzy rule table : the rule base for controller coefficient updating factor of fuzzy-based tuning BLCTC is based on

• 5.    Defuzzification : based on previous discussion COG method is used to defuzzification in this research.

has linear equation with regard to has a high-quality response.

F.R ¹ : IF e is NB and ̇ is NB, THEN а is (29) VB.

The complete rule base for supervisory controller is shown in Table 1.

Table 1: Fuzzy rule base for controller coefficients updating factor ( а )

><	FL	ML	SL	z	SR	MR	FR
NB	VB	VB	VB	в	SB	s	ZE
NM	VB	VB	В	в	MB	s	VS
NS	VB	MB	В	VB	vs	s	VS
Z	S	SB	MB	ZE	MB	SB	s
PS	VS	S	VS	VB	в	MB	VB
РМ	VS	S	MB	в	в	VB	VB
РВ	ZE	S	SB	в	VB	VB	VB

Supervisory controller is a controller to solve the unstructured uncertainties and tuning the controller coefficient. This controller consists of two parts: fuzzy logic controller and scaling factor. Fuzzy logic controller is a Mamdani’s error base inference system which has error ( е ) and change of error ( е ̇) as inputs and controller coefficient updating factor ( а ) as output. Each inputs has seven linguistic variables thus the controller’s output has 49 rules, the output is defined between [0.5 1] and it is quantized into thirteen levels. Scaling factor ( k_a and кр ) are used to limit error between [-1 1] and change of error between [-6 6]. To normalize the error and change of error scaling factors are applied ( к_а and кр ) to е and €̇ as bellows:

е_п = × е (30)

̇ = ×̇ (31)

Controller coefficient updating factor ( а ) is used to tuning the main controller to give the best possible results. It is required because the robot manipulator’s dynamic equations are highly nonlinear, the rules formulated in BLCTC through user experience are not always correct under defined and also to unstructured uncertainties. It is independent of robot manipulator dynamic parameters and depends only on current system’s performance; it is based on error and change of error. In this method the actual controller coefficient ( Л ) is obtained by multiplying the controller coefficient with

Design PID Baseline Fuzzy Tuning Proportional- Derivative

Coefficient Nonlinear Controller with Application to Continuum Robot

controller coefficient updating factor (a). The controller coefficient updating factor (a) is calculated on-line by 49 rules Mamdani’s error-based fuzzy logic methodology. According to the (24) new coefficients are calculated by;

First link

UpiD-New

Kp-New^e + K_v__Newe

+ к , _ _New

s*

Proposed CTC

20          25          30

Where;

^K p -New = ^K p ^x ^,     Kv-New^KVx ^{x a}

K—New=Kj x a

Figure 5 shows the block diagram of proposed methodology.

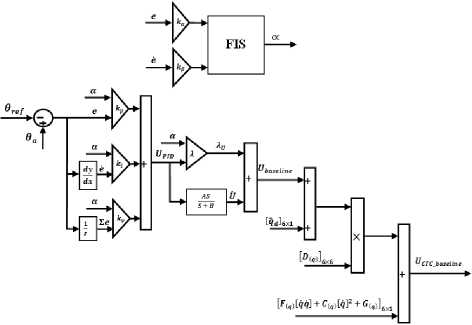
Fig. 5: Block diagram of Fuzzy Tuning Baseline Computed Torque Methodology

^TNEW-ETC = [Dq ] ^{x [[[K} p- New ^ + I^V-KewC + К—New E в] X A_New + ^^ ^{x [K} p - New^ + ^K v-New ^e + ^K ' I - New ^{E e} ]] + [q_d]] + ^(q ,

• IV.    Results and Discussion

To test of this controller, this part of research is focused on compare between computed torque controller (CTC) and fuzzy tanning baseline computed torque controller (Proposed Method). These controllers were tested by step response. The simulation was implemented by MATLAB/SIMULINK environment.

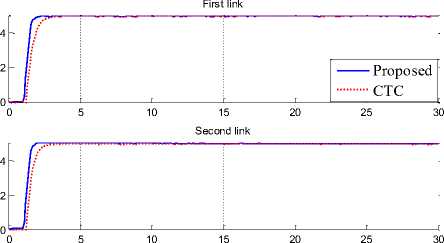
Trajectory Follow: Computed torque controller and fuzzy tuning baseline computed torque controller applied to continuum robot manipulator under condition of step trajectory response. Figure 6 shows the control of trajectory following based on two methods.

Fig. 6: Computed torque controller Vs. fuzzy tuning baseline computed torque controller

According to above graph; by comparing trajectory following response without disturbance these two controllers, proposed method’s rise time (0.4 sec) is lower than computed torque controller’s (0.5 sec). Based on Figure 6, both controllers are the same conditions; steady state error and trajectory following.

Disturbance rejection test: one of the main objectives in this research is robustness. For this reason, 40% external disturbance applied to these two controllers in MATLAB/SIMULINK environment. Figure 7 shows the power disturbance elimination in these two controller with torque load disturbance for trajectory following. According to the following graph, computed torque controller has fairly fluctuations in trajectory responses.

Third link

0           5           10           15          20          25           30

Time

Fig. 7: Computed torque controller Vs. fuzzy tuning baseline computed torque controller with torque load disturbance

Based on above graph; computed torque controller has moderately oscillation in trajectory response with regard to torque load disturbance but fuzzy tuning baseline computed torque controller has stability in trajectory responses. Based on Figure 7, by comparing trajectory response in presence of torque load disturbance in these two method, proposed method’s rise time (0.4 sec) is lower than computed torque controller’s (0.7 s). For above reasons according to adaptive methodology, fuzzy tuning baseline computed torque controller is more robust than pure computed torque controller.

• V.    Conclusion

In this research, a multi-input-multi-output online tuning fuzzy based baseline computed torque control scheme is used to simultaneously control the speed rate of six ports torque to regulate the joint variable to desired levels. The control target is to have stability and robustness in presence of external disturbance and uncertainties. The first part of this controller is baseline methodology that works based on applied PID methodology to modified PD methodology. The second part of this controller is computed torque controller; this controller is one of the best nonlinear controllers in certain system. Baseline computed torque controller is more robust than pure computed torque controller and pure baseline methodology. Online tuning methodology is applied to proposed controller to obtain the best condition in presence on uncertainty and external disturbance. The ability to use proposed methodology on a MIMO case was significant. This supervisory methodology has acceptable performance in presence of uncertainty (e.g., overshoot=0%, rise time=0.4 second, steady state error = 1e-9 and RMS error=1.8e-12).

Acknowledgment

The authors would like to thank the anonymous reviewers for their careful reading of this paper and for their helpful comments. This work was supported by the Institute of Advanced Science and Technology (IRANSSP) Research and Development Corporation Program of Iran under grant no. 2013- Persian Gulf -1A.