Detecting happiness in human face using unsupervised twin-support vector machines

Published Online August 2018 in MECS

Early Aristotelian era [1] (4th century) people are more interested to study on human behaviors especially facial expression over the year, but Physiognomy is outshined from the human behaviors. From the foundational studies of facial expression, [2] “Pathomyotmia” book has given description of expression in human and muscle movement. Through [3], lectured the artist “the Perfect imitations of ‘genuine’ facial expression”. In [4], book evolved that the principles for facial expression of human and animal, facial deformation, grouping the expression variations. In [5], “James Lange theory” states that the expression variations are derived from the presence of stimuli which evokes the physiological responses in human body. In [6], has given the study of automatic facial expression system, definition of basic six emotions in human face as well as analysis of facial expression from the muscle movement through the photographic stimuli.

Ref [7-8] has established the automatic facial expression system from facial image sequence, which analyzed the facial emotion through tracking points. Ref [9] developed the automatic facial expression system using facial feature detection and tracking points from image sequence. Since 1990s several researchers are been more interested in human emotion recognition of Human Computer Interaction (HCI), Affective computing, etc. Emotion recognition in human has established by the various mode of extraction [10] such as: physiological (EEG, ECG, etc,) and non-physiological signal (face, body, speech, text…etc.). From [10], the facial expression recognition is the best out of the various modes of extracting emotion methods. From 1990 to till now, researchers are mostly concentrating on the robustly automatic facial expression from image sequence and comparatively other modes of extracting the emotion.

Ref [11] given the details of face modeling: the state of art. In that importance of face modeling, this explained the different face models of face detection and tracking of automatic facial expression recognition. In that inference, the geometric deformable model has good face detection and tracking.

In the parameterized models, Facial Action Coding System (FACS) defines only the muscular movement of face. FACS also defines the basic six emotion in human face was given by Ekman and Friesen [12]. Ref [13-16], are developed the facial expression recognition system with FACS. In that, data computation is high, but accuracy of facial expression system is low. In order to achieve, the low data computation and high accuracy of real time facial expression recognition system by using Facial Animation Parameters (FAPs) [17]. Ref [18-20] are developed the real-time facial expression system using FAPs, where detailed about of each feature point’s movement of facial emotion are related to Action Units (AU).

In the feature and model based approaches [13-16], [21-24], [39-42] the classification are major role of the real time facial expression system. In that we survey [3133] Twin Support Vector Machines is better performance compared to the other classifier models.

• II.    Related Work

In this paper, the real-time facial expression recognition system is proposed for detecting the emotion in human from face. The proposed system is based on detecting human face using face detection, tracking and extracting the feature. Finally, understands the human emotion through face using the facial expression classifier with help of parameterized method. This paper only focuses on detecting happiness using feature vector displacement with unsupervised classifier for the real time applications. This paper, the novel method for real time facial expression, which based on:

• •    Constrained Local Method (CLM) [25] is developed for face detection and tracking from human face and it’s evolved the extracting the feature points.

• •    Second, the Twin Support Vector Machines (TWSVMs)   [31-33] is formulated for

classification of facial expression with help of Facial Animation Parameters (FAPs) [17] and [19] is extracted the features points are formed the minimal feature vector displacements.

The rest of the paper is following: Section 2 describes the novel methods for real-time facial expression system. Section 3 describes the experimental results and discussion of proposed system. Section 4 summarizes the future and conclusion.

• III.    Facial Expression Recogntion System

The system description of robust facial expression recognition system is followed in three steps: Face Detection and Tracking, Feature Extraction and Facial Expression Classifier. In the Face detection and Tracking, deformable geometric grid node (CLM) [25] for face detection and tracking from the facial image sequence. The information of face tracking is extracted the grid node features to form the features vector displacement. Then feature vector displacement is composed in Facial Expression Classifier (TWSVM) [26] for defining the emotion in human face. The proposed system architecture of real-time facial expression recognition system is shown in Fig. 1.

• A. Facial Detection and Tracking

• 3.1.    Linear shape model

In proposed system, the face detection and tracking is carried out by Constrained Local Model (CLM) (deformable geometric model fitting) as shown in Fig. 1. CLM model is non-rigid shape parameterization for local face feature detector. The steps followed for the CLM of face detection and tracking as mentioned below.

The non-rigid shape object of face is employed by

Point Distribution Model (PDM) [27]. In 2D PDM, where represented as 2D vertex mesh of 2v dimensionality shape s vectors. Building way of PDM is applied the Principal Component Analysis (PCA) to contracted the aligned non-rigid face shapes. Applied the Procrustes analysis for removing the parameters s, R, t x , t y of aligned mesh shapes before applying PCA. The 2D PDM is linearly deformed the variation of non-rigid shape and it’s composed with the global transformation, placing the shape in image frame in (1).

• x i = sR ⁽ x j ) + T^ , t y ^ T s , R , t x , t y ⁽ x j ) (1)

• 3.2.    Subspace Constrained Mean Shift

where x_i denotes i^th landmark of 2D PDM’s location, x_i denotes as mean shape of 2D PDM and pose parameters of PDM represent as p = ( s , R , t , q ).

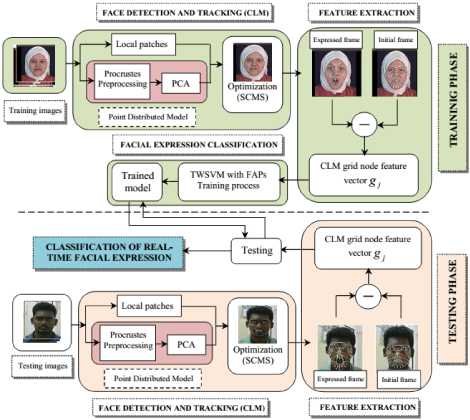
Fig.1. The proposed system architecture of real-time facial expression recognition system

In CLM fitting, merely applied the Subspace Constrained Mean Shift (SCMS) for good local (patch) search of landmark fitting and optimized the 2D PDM landmark. In exhaustive local search, use linear logistic regressors [28] which give the response maps for ith landmark position in image frame in (2).

P ( li = aligned 1 1 , x ) =

1 + exp { a Ci ( I ; x ) + в }

where l _i is a discrete random variable, which denotes whether the i^th PDM landmark is correctly aligned or not. I is an image, x is denotes as a 2D location in local images. в is regression coefficient and it’s denotes as correct the 2D landmark of local maps. C _i is the linear classifier of local detector in (3) with {x-} m g Q_v i i = 1          ^xi

(image patch) and b _i is shape vector parameters.

Ci ( I ( x i ) ) = w И I ( xi ) ;...... ; I ( x m ) ] + bi           ⁽³⁾

once the response maps of each landmark of local search have been found, the conditional independence of the Probabilistic function of local response images detection for each landmark is maximized by optimization strategies in (4).

parameterization using a least-square fit from (9).

Q ( p ) = XX |xi - x ( ^{T + 1 )} i = 1

p

n

P J = П P ( li = aligned I x i )      (4)

i = 1

The Q-function of M-step (10) is formed by using the linear shape model (6) and global objective maximizing of PDM landmark (4) with the Expectation-Maximization (EM) algorithm [31] (10).

Ap = ^J^ ^{x ( T + 1 ) -} xC; ;x ^T + ^{1 ) -} x П

with respect to p PDM parameters, x _i is parameterized of response images. In optimization strategy, Active Shape Model is used for attained the maximum response map location and minimize the weighted least squares difference between the peak responses coordinates and PDM in (5).

« Р ) = £ - i h i - «II²              (5)

i = 1

a first order Taylor expansion applied (4) is minimized of PDM landmark is

x i ” ^x c + J i ^A P                   ⁽⁶⁾

and the parameter update of solving (7).

n

A p = X w i J Г J

- 1

n

X wi^J Ц №- xc )

J ^ is denotes the pseudo-inverse of J and x (( ^{T + 1)} is denotes as i^th landmark of mean shift update parameters is given in (8). Equation (9) is the Gauss Newton update for least square PDM constraint.

B. Deformable Facial Feature Vector

The information of face detection and tracking is extracted, which is carried out for emotion in real-time human face using geometric deformable model (CLM). The extracted information of facial expression, the frame by frame facial features to formed the feature vector displacement. The information of features vector displacement is one node displacement d defined as the consecutive frame by frame of image sequence, which is difference between the grid node displacements of first to i^th node coordinates. The feature vector displacement is (11). i = 1,...... F , j = 1,...... N , where A x i , j , A y i , j are x, y axis coordinates of grid node displacement of the i^th node in j^th frame image respectively.

the current parameter is applied in p — p + A p to estimate the pose and shape. Here Jacobin is J = [ J1;...;J n ] and current shape parameter update is x = [ xC ;...; хП ] . For independent maximization and nonparametric representation of Kernel Density Estimate (KDE) [29] for each PDM landmark location is used the mean-shift algorithm [30] consists of fixed point iteration (8).

^d i , j =

^Δx i . j

^Δy i , j

a 11 ^{- a} 12     ^a 13 ^{- a} 14

a 21 ^— a 22     a 23 ^— a 24

^a 1, j + 1 ^{- a} 1, j + 2

( a i , j - a i , j + 1

a n , m + 1    a n , m + 2

x _i

- X

Mi ^ V c xi

( ( t )

a N X;  ; Ml , 7 ² I

M i     I i         ¹

„  .  / _M---4 M i (8)

^ a N I x^;y, 7 ²I |

“  y (         )

У^ Vxc xi

equation (7) is applied iteratively until met some convergence A p . Based on two step strategy, the shape constrained is optimized: i) compute the mean-shift update for each 2D PDM landmark, ii) constrain the mean-shifted landmark to remain to the PDM

F is the number of grid node (F=66 nodes of Constrained local model) and N is the number of the extracted facial images from the facial image sequence.

g j =[ d 1, j d 2, j d e , j ] ^Г j = 1, N ⁽¹²⁾

from the (12), for every sequence of the facial expression images in data set, an extracted feature vector g is formed the displacements of the every geometric grid node d , g is called the grid deformation feature vector.

C. Facial Expression Classifier

The facial feature extraction formed the minimal feature vector displacement with FAPs. The resultant of minimal feature vector displacement is formulated in the two class Twin Support Vector Machine (TWSVM) [31-

33] classify the real-time facial expression. Twin Support Vector machines (TWSVM) is constructed the two nonparallel hyperplane for each class to solve the Quadratic programming problem. In this system, we formulated the two classes TWSVM using for facial expression classifier. Let g j = {(X . ,y i )}; i = 1 k ;X e« n ;y , e { - 1, + 1} is the training dataset of facial extraction of minimal feature vector displacement. Then separating two non-parallel hyperplane of linear data of the form is (13).

For Nonlinear TWSVM is applied the kernel functions are (19).

Linear        K ( x i , X j ) = ( x i • X j )

Polynomial K ( x i , X j ) = ( x i • x j - + ^ ) d              (19)

f | x i - x j f 1

RBF        K (x., x,) = exp -  ---- i j              o^2

^x T • w (1) ⁺ b (1) = 0

^x T • w (2) ^{+ b} (2) = ⁰

separating the minimal feature vector displacement g j = ^ L in the order of positive and negative class is form using Lagrangian and Wolf dual problem (14).

Multi class TWSVM has two approach are: “One Vs One” and “One Vs All”. The “One Vs One” approach is “divide and conquer” approach consists of building one TWSVM class for each pair of subclasses. The “One Vs All” is “single approach” consist of build TWSVM which one class with all classes. This paper, we carried out the both approach of multiclass TWSVM and its more effective in “One Vs All” approach, which it’s detailed in Section 3.

mint w 1 , ^b1, 5 )   ¹|| X 1 w 1 + e 1 ^b 1||2 + c 1 e T ⁵

s . t - ( X ₂ w 1 + e ₂ b 1 ) + 5 - e ₂, 5 - 0

min( w ₂ , b 7 )   ~^2W2 + e₂b ₂||+ c₂e T 7

s.t   - ( X_xw₂ + e_xb₂ ) + 7 - e i, 7 - 0

c i , c₂ are penalty parameter and 5 , 7 are slack variables. e 1 , e 2 are vectors of one’s of suitable dimensions. From (14), apply the Karush –Kuhn-Tucker (K.K.T) conditions are formulated and obtained equation of TWSVM1 is.

A

e

A e ₁

_w (1) _b (1)

+ Г B^T e T 1 a = 0

let H = ^Г A T e T ^ , G = [ B e 1 ] and augmented vector is u = [ w 1 , b 1 ] . From (15), this is reformulated as (16).

u 1 =- ( A T A + ^ 7 ) ^{- 1} B^T a             (16)

and 5 I is regularization identity matrix for obtained the inverse matrix. Similarly for TWSVM2 obtained the (17) is.

u ₂ =- ( B^TB + J I ) ^{- 1} A T в             (17)

The weight vector and biases values are find out the two non parallel hyperplane of both classes. For validation, a new data sample is assigned to class ‘i’ by the decision function is (18).

Class i = min| x ^T w i + b i| for i = 1,2          (18)

From (18), decision surface is classified the new data depends upon which its distance is closer to hyperplane.

IV. Experimental Analysis and Discussion

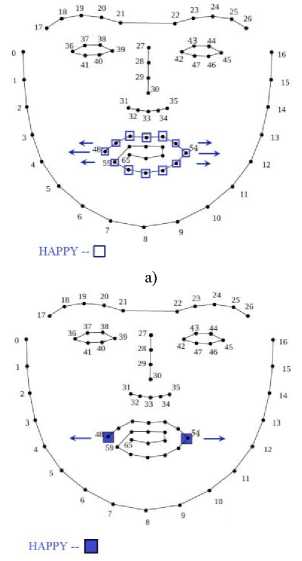
In the real-time facial expression system, the face tracking is carried out by the geometric deformable model (CLM) and feature extraction is done by linear logistic regression [25]. For classification applied two classes TWSVM in the proposed system. In proposed system, Facial Animation Parameters (FAPs) is used for details about the feature point variation in facial movement. Table 1 shown as the textual description of basic six emotion of face. From the FAPs [19], happy have major variation in mouth (Group 8 and 2). The information of extracted features of CLM is composed the feature vectors displacement. The entire and minimal feature vector displacement of happy in CLM is shown in Fig. 2.a, 2.b the blue color indicates as happy. The laughter (happy) variations are more in outer lip and corner lip region with along x-axis direction from the FAPs [19]. In our proposed system, the entire feature vector displacement has high data computation and less accuracy of variation in happy (laughter).

In order to achieve, less data computation and high accuracy, minimal feature displacement is implemented and desired results are obtained. In Fig. 2, the entire feature vector displacement has feature variation in Group 8 (outer mouth lip region) and Group 2(corner lip region) from the FAPs description. This paper, the minimal feature vector displacements have the feature variation only in Group 2 (corner lip region) as shown in Fig. 2.b.

In our system, the geometric deformable grid node (CLM) having L = 66*2 = 132 dimensions. In the g feature vector displacement of image sequence, where computed the d displacements of CLM grid node in order to form started at neutral face to expressed face (i.e. Initial frame to peak response of frame) and the expressed face to neutral state.

Table 1. Description of Basic six emotion of face, with each feature movement by FAPs

Expression	Textual description
Surprise	The eyebrows are raised. The upper eyelids are wide open, the lower relaxed. The jaw is opened.
Happy	The eyebrows are relaxed. The mouth is open and the mouth corners pulled back toward the ears.
Disgust	The eyebrows and eyelids are relaxed. The upper lip is raised and curled, often asymmetrically.
Fear	The eyebrows are raised and pulled together. The inner eyebrows are bent upward. The eyes are tense and alert.
Anger	The inner eyebrows are pulled downward and together. The eyes are wide open. The lips are pressed against each other or opened to expose the teeth.
Sad	The inner eyebrows are bent upward. The eyes are slightly closed. The mouth is relaxed.

b)

Fig.2. CLM grid of entire and minimal feature vector displacement of Happy

The CLM feature vector displacement g is employing for the classification of laughter (happy) face using two classes of TWSVM in our proposed system. In our proposed system, the real-time facial expression system of CLM is developed in C++ with open framework tool and TWSVM (Matlab) which was implemented in Intel i5 processor. In training and testing process, MMI facial expression standard database [35], Mahnob-Laughter database[36], Cohn-Kanade (CK) [37], extended-CK (CK+) [38], and real time datasets [43] is used in our proposed system of video rate is 30 Frames/sec are respectively and only frontal face image sequence are captured.

A Training phase

In training process, let g j is feature vector displacements of extracted MMI, Mahnob-Laughter , CK, CK+ and real time data sets of facial image sequence as X i   i = 1,..... ,N ; N = 6 , emotions in face, which is

, shown in Fig. 3.

a) MMI Facial Expression Database

b) Cohn-Kanade Database

c) Extended Cohn-Kanade Database

d) MAHNOB-Laughter

e) Real time Expression data

Fig.3. Training and Testing phase with standard and real time database

• 4.1.    Happy

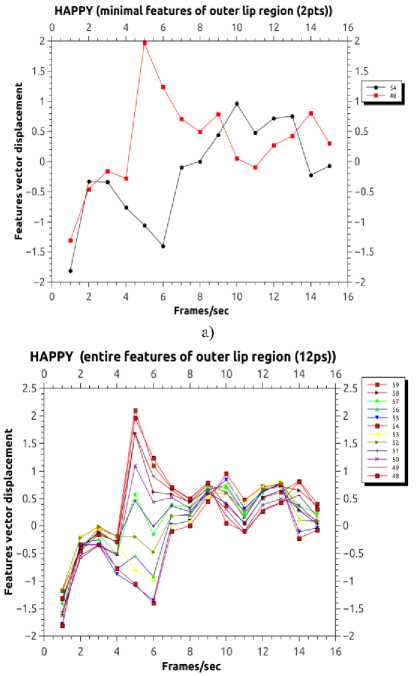
  In training process of laughter/happy, the feature vector displacements were formed by captured MMI, Mahnob-Laughter , CK, CK+ and real time datasets [3539]. The major facial feature movements of happy is in Group 8 (outer lip mouth region) has 12 features points and Group 2 (corner lip region) has 2 features point is horizontally (x-axis) expanded, given by FAPs. The entire feature vector displacements of happy which belong the temporal segment of outer lip region (Group 8) and corner lip mouth region (Group 2) as shown in Fig. 4.a. The minimal feature vector displacement of happy is in temporal segments of corner lip mouth region (Group 2) as shown in Fig. 4.b.

In entire feature vector displacements of happy in CLM have been used 12 feature points (49th - 66th points) as shown in Fig. 4.a. The minimal feature vector displacements in CLM have been used only 2 feature points (49th and 54th point) as shown in Fig. 4.b.

Group 8 (outer lip mouth). In our proposed system, the minimal feature vector displacements are formed by only Group 2 as shown in Fig. 4.b. The minimal feature point was selected based on, where peak responses are high (i.e. expression of face in image sequence), less data computation, improvement of accuracy, compared to entire features points.

a)

b)

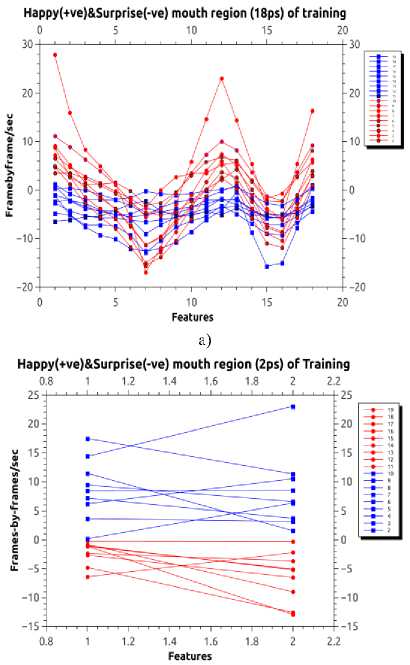
In training process, the classification of happy, the entire feature vector displacements of mouth region (i.e. Group 8 and Group 2) were computed on two classes of TWSVM attained the Non-Linear classification as shown in Fig. 5.a. In “One vs One” and “One vs All” classification of laughter/happy, the variation of happy have been taken as (+ve) positive class and others (such as Surprise, Anger, etc.,) have been as (-ve) negative class.

Now, the entire feature vector displacement is achieved Non-linear case of happy, it cases the affect of classification. The minimal feature vector displacement also attained the non-linear case of classification of laughter/happy as shown in Fig. 5.b. In order to achieve, the linear case of laughter/happy of the minimal feature vector displacement, the normalization and transformation of mapping function is applied for obtaining the linear separable of corner lip region. The enlargement view of a linear separable of laughter (happy) in corner lip mouth region as shown in Fig. 5.b.

In the training process, we had taken as example of happy as positive class (blue) and surprise have been taken as negative class (red) of corner lip and outer lip mouth region. The trained model was taken as 10 subjects of standard database respectively as shown in Fig. 5.a and 5.b. But we totally have taken 592 different subjects for training and testing process of standard databases. From the trained model of linear case, the real time facial expression of various laughter/happy is classify by the decision surface of TWSVM (17).

a)

b)

• B.    Testing process

In testing process, the real time facial data is compressed of all basic six emotions which was taken from 592 different subjects is shown in Fig. 2. The data was captured in certain environment and video rate is 30 frames/sec. In testing process, where evaluated with the CLM face tracking and extracted features points to form the minimal features vector displacements. From the information of minimal feature vector displacements was applied on the decision surface of trained model for classification of facial expression of laughter/happy various. In our proposed system, the facial expression classifications of the minimal feature vector displacements of Happy and other emotions are shown in Fig. 6-11. The validations of real-time facial expression system of refer the link [35].

• C.    Data scaling and validation of Laughter/Happy

In Happy, the real time data of minimal feature vector displacements of the corner lip mouth region (Group 2) was implemented in decision surface of happy train model. From the resultant of deformable feature vector was applied in Min-Max and Z-form Normalization (20) are best approaches in data scaling. Then the values were substituted in various multiclass TWSVM approaches for data validation.

Min - Max ( - 1,1): f ( x ) =

Z - Norm :        f ( x ) =

|    x - Max ( x )

( Max ( x ) - Min ( x )

- 1

x - ц a

In training and testing process used 4 standard database and one real time database. In this system used 592

subject of different emotion. Both training and testing phase was applied 2 fold–cross validations, randomly split the data to training model of happy and testing the data. In this Paper, compared the two classifier technique with cross-data validations for the state of art are: the supervised SVM [34] (LIBSVM tool) and TWSVM (Unsupervised). From table 2-11 and Fig. 6-8 are shown as the detecting happiness using supervised SVM [34] (LIBSVM) respectively. From table 12-21 and Fig. 9-11 are shown as the detecting happiness using unsupervised TWSVM respectively.

• 4.2.    Supervised SVM:

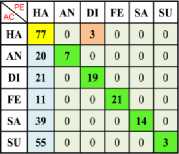
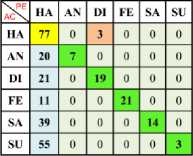
In Table 2, 3 and 4 has shown the confusion matrix of Happy (One Vs One) with Linear, Polynomial and RBF SVM of Max-Min Normalization are respectively. In Table 5, 6 and 7 has shown the confusion matrix of Happy (One Vs One) with Linear, Polynomial and RBF SVM of Z- Normalization are respectively.

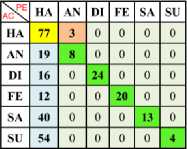
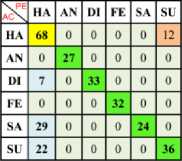
Table 2. Confusion Matrix of Happy (One vs One) Using Linear SVM Kernel with Min-Max Normalization

a) Ha Vs An

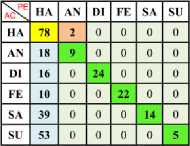
b) Ha Vs Di

c) Ha Vs Fe

e) Ha Vs Su

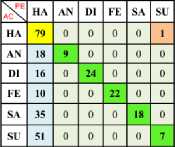
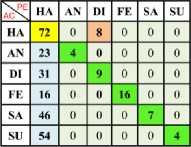
Table 3. Confusion Matrix of Happy (One vs One) Using Polynomial SVM Kernel with Min-Max Normalization

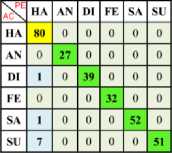
b) Ha Vs Di             c) Ha Vs Fe             d) Ha Vs Sa             e) Ha Vs Su

a) Ha Vs An

	HA	AN	DI	FE	SA	SU
HA	80	0	0	0	0	0
AN	16	11	0	0	0	0
DI	13	0	27	0	0	0
FE	9	0	0	23	0	0
SA	23	0	0	0	30	0
SU	46	0	0	0	0	12

AcX	HA	AN	DI	FE	SA	SU
HA	77	0	0	0	3	0
AN	20	7	0	0	0	0
DI	19	0	21	0	0	0
FE	11	0	()	21	0	0
SA	40	0	0	0	13	0
SU	54	0	0	0	0	4

	HA	AN	1)1	FE	SA	SU
HA	79	0	0	0	0	1
AN	17	10	0	0	0	0
DI	16	0	24	0	0	0
FE	9	0	0	23	0	0
SA	34	0	0	0	19	0
SU	54	0	0	0	0	4

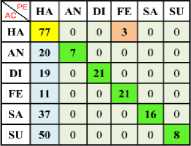
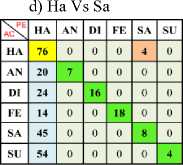
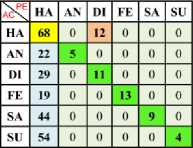
Table 4. Confusion Matrix of Happy (One vs One) Using RBF SVM Kernel with Min-Max Normalization

b) Ha Vs Di

c) Ha Vs Fe

d) Ha Vs Sa

e) Ha Vs Su

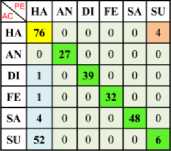
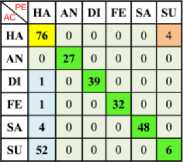
Table 5. Confusion Matrix of Happy (One vs One) Using Linear SVM Kernel with Z Normalization

a) Ha Vs An

a) Ha Vs An

b) Ha Vs Di

c) Ha Vs Fe

d) Ha Vs Sa             e) Ha Vs Su

	HA	AN	DI	FE	SA	SU		HA	AN	DI	FE	SA	SU
HA	69	0	0	0	11	0	HA	77	0	0	0	0	3
AN	21	6	0	0	0	0	AN	19	8	0	0	0	0
DI	26	0	14	0	0	0	DI	15	0	25	0	0	0
FE	18	0	0	14	0	0	FE	12	0	0	20	0	0
SA	45	0	0	0	8	0	SA	37	0	0	0	16	0
SU	54	0	0	0	0	4	SU	54	0	0	0	0	4

Table 6. Confusion Matrix of One vs One) Using Polynomial SVM Kernel with Z Normalization

• a)    HA Vs All (Linear)

• b)    HA Vs All (Poly)

• c)    HA Vs All (RBF)

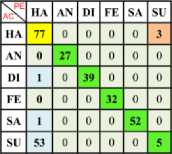
a) Ha Vs An            b) Ha Vs Di             c) Ha Vs Fe             d) Ha Vs Sa             e) Ha Vs Su

	HA	AN	1)1	FE	SA	SU	\^	HA	AN	DI	FE	SA	SU		HA	AN	DI	FE	SA	SU	ACX	HA	AN	DI	FE	SA	SU		HA	AN	DI	FE	SA	SU
НА	80	0	0	0	0	0	HA	80	0	0	0	0	0	HA	80	0	0	0	0	0	HA	80	0	0	0	0	0	HA	80	0	0	0	0	0
AN	16	11	0	0	0	0	AN	3	24	0	0	0	0	AN	1	26	0	0	0	0	AN	0	27	0	0	0	0	AN	16	11	0	0	0	0
DI	12	0	28	0	0	0	DI	0	0	40	0	0	0	DI	0	0	40	0	0	0	DI	0	0	40	0	0	0	DI	13	0	27	0	0	0
FE	8	0	0	24	0	0	FE	5	0	0	27	0	0	FE	1	0	0	31	0	0	FE	0	0	0	32	0	0	FE	9	0	0	23	0	0
SA	20	0	0	0	33	0	SA	2	0	0	0	51	0	SA	0	0	0	0	53	0	SA	0	0	0	0	53	0	SA	24	0	0	0	29	0
SU	45	0	0	0	0	13	SU	9	0	0	0	0	49	SU	5	0	0	0	0	53	SU	1	0	0	0	0	57	SU	47	0	0	0	0	11

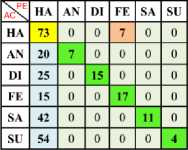
Table 7. Confusion Matrix of One vs one Using RBF SVM Kernel with Z Normalisation

a) Ha Vs An            b) Ha Vs Di             c) Ha Vs Fe             d) Ha Vs Sa             e) Ha Vs Su

	HA	AN	DI	FE	SA	SU	Ж H'	AN	DI	FE	SA	SU	\PE	HA	AN	DI	FE	SA	SU	\PE	HA	AN	DI	FE	SA	SU	X	HA	AN	DI	FE	SA	SU
HA	80	0	0	0	0	0	HA 70	0	10	0	0	0	HA	76	0	0	4	0	0	HA	69	0	0	0	11	0	HA	79	0	0	0	0	1
AN	17	10	0	0	0	0	AN 20	7	0	0	0	0	AN	19	8	0	l)	0	0	AN	21	6	0	0	0	0	AN	19	8	0	0	0	0
DI	14	0	26	0	0	0	DI 28	0	12	0	0	0	DI	16	0	24	0	0	0	DI	27	0	13	0	0	0	DI	16	0	24	0	0	0
FE	13	0	0	19	0	0	FE 18	0	0	14	0	0	FE	14	0	0	18	0	0	FE	18	0	0	14	0	0	FE	12	0	0	20	0	0
SA	32	0	0	0	21	0	SA 46	0	0	0	7	0	SA	32	0	0	0	21	0	SA	44	0	0	0	9	0	SA	38	0	0	0	15	0
SU	51	0	0	0	0	7	SU 56	0	0	0	0	2	SU	52	0	0	0	0	6	SU	54	0	0	0	0	4	SU	53	0	0	0	0	5

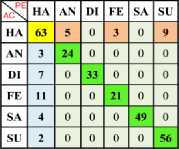
Table 8. Confusion Matrix of One vs All Using Linear, Polynomial, RBF SVM Kernel with Min-Max Normalization

Table 9. Confusion Matrix of One vs All Using Linear, Polynomial RBF SVM Kernel with Z-Normalization

a) Ha Vs All (Linear)

b) Ha Vs All (Poly)

c) Ha Vs All (RBF)

a) Min-Max

SVM-Kernel	(One vs One) (HA)	Ace (%)	Precision	Recall	F-mea
Lin	AN	52.414	0.36449	0.975	3.9
Lin	DI	38.621	0.29752	0.9	3.6
Lin	FE	51.724	0.35981	0.9625	3.85
Lin	SA	44.483	0.32618	0.95	3.8
Lin	SU	54.828	0.37799	0.9875	3.95
Pol	AN	54.828	0.37799	0.9875	3.95
Pol	DI	48.621	0.34529	0.9625	3.85
Pol	FE	63.103	0.42781	1	4
Pol	SA	49.31	0.34842	0.9625	3.85
Pol	SU	54.828	0.37799	0.9875	3.95
RBF	AN	53.448	0.37089	0.9875	3.95
RBF	DI	41.379	0.3125	0.9375	3.75
RBF	FE	62.414	0.42328	1	4
RBF	SA	45.517	0.3319	0.9625	3.85
RBF	SU	53.793	0.37264	0.9875	3.95

Table 10. Validation table of Happy using MIN-Max and Z-form Normalization

b) Z-form

SVM-Kemel	(One One) (Ha)	Acc (%)	Precision	Recall	F-mea
Lin	AN	50.345	0.35321	0.9625	3.85
Lin	DI	37.931	0.28814	0.85	3.4
Lin	FE	43.793	0.31878	0.9125	3.65
Lin	SA	39.655	0.29614	0.8625	3.45
Lin	SU	51.724	0.35981	0.9625	3.85
Pol	AN	65.172	0.44199	1	4
Pol	DI	93.448	0.80808	1	4
Pol	FE	97.586	0.91954	1	4
Pol	SA	99.655	0.98765	1	4
Pol	SU	62.414	0.42328	1	4
RBF	AN	56.207	0.38647	1	4
RBF	DI	38.621	0.29412	0.875	3.5
RBF	FE	52.759	0.36364	0.95	3.8
RBF	SA	39.655	0.29614	0.8625	3.45
RBF	SU	52.069	0.36406	0.9875	3.95

Table 11. Validation table of Happy using MIN-Max and Z-form Normalization a) Min-Max                                           b) Z-form

SVM-Kernel	Acc (%)	Precision	Recall	F-mea
Linear	80	0.583	0.9625	3.85
Pol	96.89	0.8988	1	4
RBF	78.62	0.5671	0.95	3.8

SVM-Kernel	Acc (%)	Precision	Recall	F-mea
Linear	74.48	0.5230769	0.85	3.4
Pol	100	1	I	4
RBF	75.86	0.5396825	0.85	3.4

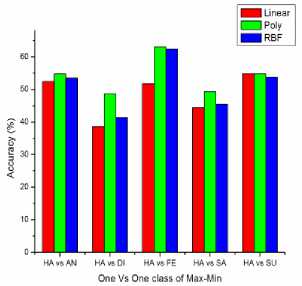
Fig.6. Bar chart of the overall accuracy of Happy (One vs One class ) (Max-Min)with all SVM kernel

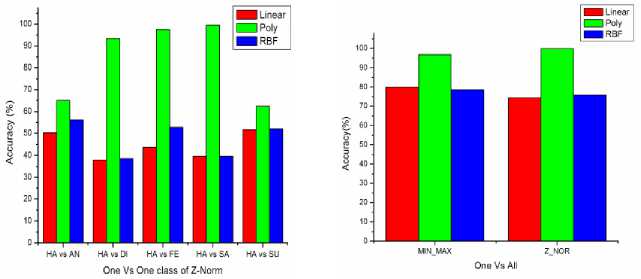
Fig.7. Bar chart of the overall accuracy of Happy (One vs One) class (Z_Norm) with all SVM kernel

Fig.8. Bar chart of the overall accuracy of Happy (One vs All) class (Z_Norm) with all SVM kernel

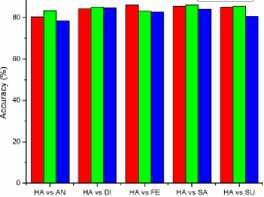
In Table 10 has shown as the validation of (One Vs One) Happy with all kernel using Max-min and Z-norm. In 10.a, the Linear, Poly, RBF SVM has been achieved 48.13%, 54.137% and 51.31% average accuracy using Max-Min normalization. In 10.b, the Linear Poly RBF SVM has been achieved 44.68%, 83.65% and 47.86% average accuracy using Z-normalization. In this, One vs One class of happy using both Max-Min and Z-norm has reached high accuracy in Poly SVM has 83.65% compared to other SVM Kernel.

In Table 8 and 9 are shown as the Confusion matrix (One Vs All) of Happy with all kernel using Max-Min and Z-norm. In Table 11 is shown as the validation of (One Vs All) Happy with all kernel using Max-min and Z-norm. From the Table 11.a, Linear, Poly, and RBF SVM has been achieved 80%, 96.89% and 78.92% overall accuracy using Max-Min norm. In Table 11.b, Linear, Poly, RBF SVM has been achieved 74.48%, 100% and 75.86% overall accuracy using Z norm. From Table 11, Happy (One Vs All) using Max-Min and Z-norm has high accuracy in Poly SVM has 100% compared to the other kernel. From the validation analysis, the “One Vs All” Multiclass SVM of Happy using Z-Norm is the best resultant value for happy classification with minimal feature vector, which is compared to “One Vs One” using both norm and “One Vs All” using Min-Max. The comparison bar charts are shown in Fig. 6 and 7, which “One Vs One” of Min-Max and Z-norm. The Comparison Bar chart is shown Fig 8 of “One Vs All” of Min-Max and Z-norm. In Fig. 6, 7 and 8, red indicates as Linear SVM, green indicates as Poly SVM and blue indicates as RBF SVM. From the Fig. 6, 7 and 8 shown the Z-norm with Poly SVM of Happy has high overall accuracy is 100% achieved which compared to the other approaches of multiclass SVM.

• 4.3.    Unsupervised TWSVM:

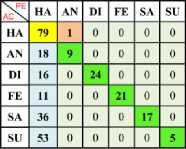
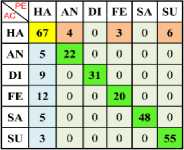
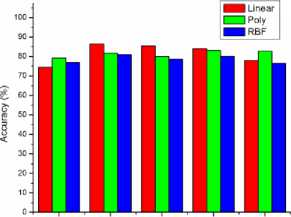
In Table 12, 13 and 14 are shown the confusion matrix of Happy (One Vs One) with Linear, Polynomial and RBF TWSVM of Max-Min Normalization are respectively. In Table 15, 16 and 17 are shown the confusion matrix of Happy (One Vs One) with Linear, Polynomial and RBF TWSVM of Z- Normalization are respectively. In Table 20 are shown as the validation of (One Vs One) Happy with all kernel using Max-min and Z-norm. In 20.a, the Linear, Poly, RBF TWSVM has been achieved 84.34%, 84.68% and 82.18% average accuracy using Max-Min normalization. In 20.b, the Linear, Poly, RBF TWSVM has been achieved 81.745%, 81.39% and 78.64% average accuracy using Z-normalization. In this, “One vs One” class of happy using both Max-Min and Z-norm has reached high accuracy in Poly TWSVM (Min-Max) is 84.68% compared to other TWSVM Kernel.

In Table 18 and 19 are shown the confusion matrix (One Vs All) of Happy with all kernel using Max-Min and Z-norm. In Table 21 is shown as the validation of (One Vs All) Happy with all kernel using Max-min and Z-norm. From the Table 21.a, Linear, Poly, RBF TWSVM has 85.62%, overall accuracy are achieved using Max-Min norm. In Table 21.b, Linear, Poly, RBF TWSVM has been achieved 85.62%, 83.79% and 84.82% overall accuracy using Z-norm. In Table 11, Happy (One Vs All) using Max-Min and Z-norm has high accuracy in Poly TWSVM is 83.79% compared to the other kernel. The reason for Poly TWSVM of Z-norm is better resultant, which is the F-measure value has higher compared to the all kernel. From the validation analysis, the “One Vs All” Multiclass TWSVM of Happy using Z-Norm is the best resultant value for happy classification with minimal feature vector, which is compared to “One Vs One” using both norm and “One Vs All” using MinMax. The comparison bar charts are shown in Fig. 9, 10, which “One Vs One” of Min-Max and Z-norm. The Comparison Bar chart shown in Fig. 11 is “One Vs All” of Min-Max and Z-norm. In Fig. 9, 10 and 11, red indicates as Linear TWSVM green indicates as Poly TWSVM and blue indicates as RBF TWSVM. From the Fig. 9, 10 and 11 shown as the Z-norm with Poly

TWSVM of Happy has high overall accuracy is 83.79% achieved which compared to the other approaches of multiclass TWSVM. From the validation and comparison of all kernels with both normalizations has high performance in Unsupervised TWSVM (Poly Kernel) of Z-norm, which it’s compared to the supervised SVM. The reasons of Poly TWSVM have high accuracy with high F-measure value, computational less and more reliability. Also it’s very suitable for real time facial expression system to detect unlabelled new datasets with more input data or features for better performance.

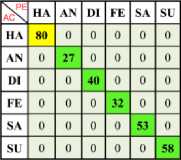
Table 12. Confusion Matrix of Happy (One vs One) Using Linear TWSVM Kernel with Min-Max Normalization

• a) Ha Vs An           b) Ha Vs Di          c) Ha Vs Fe              d) Ha Vs Sa          e) Ha Vs Su

АС\	HA	AN	DI	FE	SA	SU	AC\	HA	AN	DI	FE	SA	SU	acX	HA	AN	DI	FE	SA	SU	ACX	HA	AN	DI	FE	SA	SU	Xе	HA	AN	DI	FE	SA	SU
НА	69	11	0	0	0	0	HA	52	0	28	0	0	0	HA	51	0	0	29	0	0	HA	57	0	0	0	23	0	HA	66	0	0	0	0	14
AN	8	19	0	0	0	0	AN	1	26	0	0	0	0	AN	1	26	0	0	0	0	AN	2	25	0	0	0	0	AN	7	20	0	0	0	0
DI	20	0	20	0	0	0	DI	3	0	37	0	0	0	DI	3	0	37	0	0	0	DI	6	0	34	0	0	0	DI	15	0	25	0	0	0
FE	19	0	0	13	0	0	FE	3	0	0	29	0	0	FE	5	0	0	27	0	0	FE	9	0	0	23	0	0	FE	16	0	0	i6	0	0
SA	13	0	0	0	40	0	SA	2	0	0	0	51	0	SA	2	0	0	0	51	0	SA	4	0	0	0	49	0	SA	10	0	0	0	43	0
SU	3	0	0	0	0	55	SU	2	0	0	0	0	56	SU	2	0	0	0	0	56	SU	2	0	0	0	0	56	SU	2	0	0	0	0	56

Table 13. Confusion Matrix of Happy (One vs One) Using Polynomial TWSVM Kernel with Min-Max Normalization

• a) Ha Vs An            b) Ha Vs Di           c) Ha Vs Fe               d) Ha Vs Sa           e) Ha Vs Su

ACX	HA	AN	DI	FE	SA	SU	ACX	HA	AN	DI	FE	SA	SU	ACX	HA	AN	DI	FE	SA	SU	ACX	HA	AN	DI	FE	SA	SU		HA	AN	DI	FE	SA	SU
HA	61	19	0	0	0	0	HA	60	0	20	0	0	0	HA	73	0	0	7	0	0	HA	60	0	0	0	20	0	HA	62	0	0	0	0	18
AN	2	25	0	0	0	0	AN	1	26	0	0	0	0	AN	4	23	0	0	0	0	AN	1	26	0	0	0	0	AN	1	26	0	0	0	0
DI	7	0	33	0	0	0	DI	5	0	35	0	0	0	DI	11	0	29	0	0	0	DI	3	0	37	0	0	0	DI	5	0	35	0	0	0
FE	15	0	0	17	0	0	FE	13	0	0	19	0	0	FE	16	0	0	16	0	0	FE	11	0	0	21	0	0	FE	14	0	0	18	0	0
SA	4	0	0	0	49	0	SA	3	0	0	0	50	0	SA	8	0	0	0	45	0	SA	3	0	0	0	50	0	SA	3	0	0	0	50	0
SU	1	0	0	0	0	57	SU	1	0	0	0	0	57	SU	3	0	0	0	0	55	SU	2	0	0	0	0	56	SU	1	0	0	0	0	57

Table 14. Confusion Matrix of Happy (One vs One) Using RBF TWSVM Kernel with Min-Max Normalization

• a) Ha Vs An            b) Ha Vs Di           c) Ha Vs Fe               d) Ha Vs Sa           e) Ha Vs Su

AC\	HA	AN	DI	FE	SA	SU		HA	AN	DI	FE	SA	SU	AC\	HA	AN	DI	FE	SA	SU		HA	AN	DI	FE	SA	SU		HA	AN	DI	FE	SA	SU
HA	76	4	0	0	0	0	HA	66	0	14	0	0	0	HA	73	0	0	7	0	0	HA	72	0	0	0	8	0	HA	76	0	0	0	0	4
AN	6	21	0	0	0	0	AN	3	23	0	0	0	0	AN	4	23	0	0	0	0	AN	4	23	0	0	0	0	AN	5	22	0	0	0	0
DI	18	0	12	0	0	0	DI	6	0	34	0	0	0	DI	11	0	29	0	0	0	DI	8	0	32	0	0	0	DI	17	0	23	0	0	0
FE	21	0	0	11	0	0	FE	15	0	0	17	0	0	FE	16	0	0	16	0	0	FE	16	()	0	16	0	0	FE	18	0	0	14	0	0
SA	8	0	0	0	45	0	SA	4	0	0	0	49	0	SA	8	0	0	0	45	0	SA	6	0	0	0	47	0	SA	9	0	0	0	44	0
SU	3	0	0	0	0	55	SU	2	0	0	0	0	56	SU	4	0	0	0	0	54	SU	4	0	0	0	0	54	SU	3	0	0	0	0	55

Table 15. Confusion Matrix of Happy (One vs One) Using Linear TWSVM Kernel with Z Normalization

• a) Ha Vs An            b) Ha Vs Di           c) Ha Vs Fe               d) Ha Vs Sa           e) Ha Vs Su

AC\	HA	AN	DI	FE	SA	SU			НЛ	AN	DI	FE	SA	SU		ACX	HA	AN	DI	FE	SA	SU	ACX.	HA	AN	DI	FE	SA	SU		HA	AN	DI	FE	SA	SU
HA	69	11	0	0	0	0		HA	52	0	28	0	0	0		HA	51	0	0	29	0	0	HA	57	0	0	0	23	0	HA	66	0	0	0	0	14
AN	8	19	0	0	0	0		AN	1	26	0	0	0	0		AN	1	26	0	0	0	0	AN	2	25	0	0	0	0	AN	7	20	()	0	0	0
DI	20	0	20	0	0	0		DI	3	0	37	0	0	0		DI	3	0	37	0	0	0	DI	6	0	34	0	0	0	DI	15	0	25	0	0	0
FE	19	0	0	13	0	0		FE	3	0	0	29	0	0		FE	5	0	0	27	0	0	FE	9	0	0	23	0	0	FE	16	0	0	16	0	0
SA	13	0	0	0	40	0		SA	2	0	0	0	51	0		SA	2	0	0	0	51	0	SA	4	0	0	0	49	0	SA	10	0	0	0	43	0
SU	3	0	0	0	0	55		SU	2	0	0	0	0	56		SU	2	0	0	0	0	56	SU	2	0	0	0	0	56	SU	2	0	0	0	0	56

Table 16. Confusion Matrix of (One vs One) Using Polynomial TWSVM Kernel with Z Normalization

• a) Ha Vs An            b) Ha Vs Di           c) Ha Vs Fe               d) Ha Vs Sa           e) Ha Vs Su

  AC\	HA	AN	DI	FE	SA	SU	AC\	HA	AN	DI	FE	SA	SU	AC\	HA	AN	DI	FE	SA	SU	AC\	HA	AN	DI	FE	SA	SU	aX	HA	AN	DI	FE	SA	SU
  HA	72	8	0	0	0	0	HA	67	0	13	0	0	0	HA	69	0	0	II	0	0	HA	69	0	0	0	11	0	HA	71	0	0	0	0	9
  AN	7	20	0	0	0	0	AN	6	21	0	0	0	0	AN	7	20	0	0	0	0	AN	6	21	0	0	0	0	AN	4	23	0	0	0	0
  DI	15	0	25	0	0	0	DI	12	0	28	0	0	0	DI	15	0	25	0	0	0	DI	10	0	30	0	0	0	DI	13	0	27	0	0	0
  FE	15	0	0	17	0	0	FE	13	0	0	19	0	0	FE	14	0	0	18	0	0	FE	13	0	0	19	0	0	FE	14	0	0	18	0	0
  SA	9	0	0	0	24	0	SA	6	0	0	0	47	0	SA	8	0	0	0	45	0	SA	6	0	0	0	47	0	SA	8	0	0	0	45	0
  SU	2	0	0	0	0	56	SU	3	0	0	0	0	55	SU	3	0	0	0	0	55	SU	3	0	0	0	0	55	SU	2	0	0	0	0	56

  Table 17. Confusion Matrix of (One vs One) Using RBF TWSVM Kernel with Z Normalization

  
  

  a) Ha Vs An

  
  

  c) Ha Vs Fe

  
  

  d) Ha Vs Sa

  
  
  
  
  

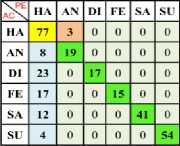
  b) Ha Vs Di

  
  
  
  
  
  
  
  
  

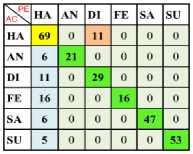
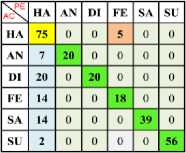
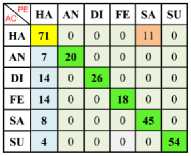
  e) Ha Vs Su

  
  
  
  
  

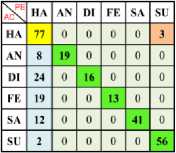
  Table 18. Confusion Matrix of (One vs All) Using Linear, Polynomial, RBF TWSVM Kernel with Max-Min Normalization

  
  

  a) Ha Vs All (Linear)

  
  

  b) Ha Vs All (Poly)

  
  

  c) Ha Vs All (RBF)

  
  
  
  
  
  
  
  
  
  
  

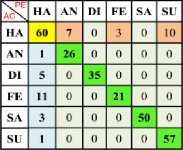
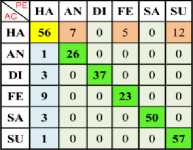
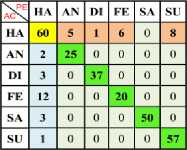
  Table 19. Confusion Matrix of (One vs All) Using Linear, Polynomial RBF TWSVM Kernel with Z-Normalization

  
  

  a) Ha Vs All (Linear)

  
  

  b) Ha vs All (Poly)

  
  

  c) Ha Vs All (RBF)

  
  
  
  
  
  
  
  
  
  
  

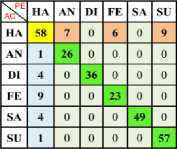
  a) Min-Max

  SVM- Kernel	(One vs One) (HA)	Acc (%)	Precision	Recall	F-mea
  Lin	AN	80.345	0.6036	0.8375	3.35
  Lin	DI	84.483	0.76923	0.625	2.5
  Lin	FE	86.207	0.77778	0.7	2.8
  Lin	SA	85.517	0.70652	0.8125	3.25
  Lin	SU	85.172	0.69072	0.8375	3.35
  Pol	AN	83.448	0.67778	0.7625	3.05
  Pol	DI	85.172	0.72289	0.75	3
  Pol	FE	83.103	0.63478	0.9125	3.65
  Pol	SA	86.207	0.75	0.75	3
  Pol	SU	85.517	0.72093	0.775	3.1
  RBF	AN	78.571	0.57576	0.95	3.8
  RBF	DI	84.775	0.6875	0.825	3.3
  RBF	FE	82.759	0.62931	0.9125	3.65
  RBF	SA	84.138	0.65455	0.9	3.6
  RBF	SU	80.69	0.59375	0.95	3.8

  Table 21. Validation table of Happy using MIN-Max and Z-form Normalization

  
  

  Table 20. Validation table of Happy using MIN-Max and Z-form Normalization

  b) Z-form

  SVM-Kernel	(One vs One) (Ha)	Acc (%)	Precision	Recall	F-mea
  Lin	AN	74.483	0.52273	0.8625	3.45
  Lin	DI	86.552	0.8254	0.65	2.6
  Lin	FE	85.517	0.79688	0.6375	2.55
  Lin	SA	84.138	0.7125	0.7125	2.85
  Lin	SU	77.931	0.56897	0.825	3.3
  Pol	AN	79.259	0.6	0.9	3.6
  Pol	DI	81.724	0.62617	0.8375	3.35
  Pol	FE	80	0.59483	0.8625	3.45
  Pol	SA	83.103	0.64486	0.8625	3.45
  Pol	SU	82.759	0.63393	0.8875	3.55
  RBF	AN	76.897	0.5461	0.9625	3.85
  RBF	DI	81.034	0.61062	0.8625	3.45
  RBF	FE	78.621	0.56818	0.9375	3.75
  RBF	SA	80.137	0.60169	0.865854	3.46341
  RBF	SU	76.552	0.54225	0.9625	3.85

  
  

  a) Min-Max                                   b) Z-form

  
  

  SVM- Kemel	Acc (%)	Precision	Recall	F-mea
  Linear	85.862	0.7407407	0.75	3
  Pol	85.862	0.7671233	0.7	2.8
  RBF	85.862	0.7407407	0.75	3

  
  

  SVM- Kemel	Acc (%)	Precision	Recall	F-mea
  Linear	85.862	0.7532468	0.725	2.9
  Pol	83.793	0.6633663	0.8375	3.35
  RBF	84.828	0.7	0.7875	3.15

  
  

  EZ1 Linear

  

  One vs One Of Max-Mln

  Fig.9. Bar chart of the overall accuracy of Happy (One vs One class) (Max-Min) with all TWSVM kernel

  
  
  

  One Vs One (Z-Norm)

  Fig.10. Bar chart of the overall accuracy of Happy (One vs One) class (Z_Norm) with all TWSVM kernel

  
  
  

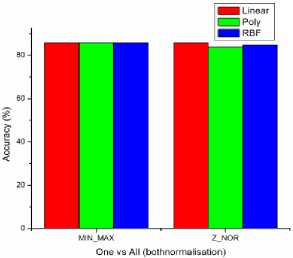
  Fig.11. Bar chart of the overall accuracy of Happy (One vs All) class (Z_Norm) with all TWSVM kernel

  
  

• V. Conclusion

In this paper proposed the real-time facial expression recognition system of minimal facial feature vectors from the facial image sequence. In training phase accomplished the face identification and tracking in the standard database video with help of CLM. Consequently, an extraction of facial feature of CLM to developed the entire and minimal feature vectors. From features vector displacement is employed in Twin-Support Vector Machines along with Facial Animation Parameters (FAPs) to accomplish the trained model of Facial Expression Classification system. Similarly, the testing process, the real-time facial expression systems are developed. Subsequently, the proposed system estimated the real time facial expression recognition with minimum facial feature is robust, when the results of the testing data of minimal facial feature vector are applied in trained model of facial expression classification system.

The minimal facial feature vectors have more accuracy, less data computation, good reliability, when it’s compared to the entire facial features vector. This paper is detailed about only happy emotion of real time human facial and database, used with minimal and entire feature vector. In addition, minimum facial feature vectors are obtained  in feature reduction of facial expression recognition with have high accuracy. This paper has been carried out the cross data validation among Supervised SVM and Unsupervised TWSVM. This paper, the Z-norm with Poly TWSVM of Happy has achieved overall high accuracy 83.79% which it’s compared to the other approaches of multiclass TWSVM and SVM. Conclude with our future work are other emotions of feature reduction of the real time facial expression recognition, head pose variation, multiclass of emotion classification and along with profile face image sequence (i.e. side view of face image) for developing the Human-Computer Interaction (HCI) application.

Acknowledgments

The authors would like to thank my research colleague for real time dataset from VIT University Chennai campus.