Determination of coefficient of surface efficiency at vacuum-atmospheric drying of large-dispersed food materials in a dense layer

Introduction                                   [1]. Study of heat and mass transfer processes in

Drying is a complex operation involving     drying plants, both vacuum and atmospheric, is simultaneous heat and mass transfer processes     based on the determination of heat and mass transfer coefficients. It is known that the values of the heat transfer and mass coefficients are

determined by the relations: ΔQ α=     , (1) f Δt AM ΔM (2) β= M or β= f Δр f ΔХ where: β - mass transfer coefficient, s/m; α - heat transfer coefficient, W/(m2·K); ΔQ – quantity of heat spent on heating of material, W; ΔM – amount of moisture removed the dried material, kg/s; Δt – temperature difference between heating surface or environment and material 0C; Δp - difference of partial pressures of water vapor corresponding to temperature of material and temperature of condensation of steam, Pa; ΔX – difference in moisture contents of air near surface of material and in environment kg/kg; f – surface area of vaporization, m2.

In case of drying the dispersed material in a dense layer (particles in form of ball, cube, parallelepiped, etc.) in determining the magnitudes included in the equations (1) and (2), the greatest difficulty is to estimate the actual area of evaporation surface. This is due to fact that material particles located in a dense layer partially deformed and overlap surfaces of each other (figure 2) and as a result the actual or active surface of heat and mass transfer will be less than total surface of the particles.

J.M. P. Q. Delgado, A.G. Barbosa de Lima also claims that the body shape has a direct influence on the drying and heating kinetics since this parameter is directly related to the area/volume of the body. The higher area/volume relationships, the solid dry faster [2].

In studies of a number of scientists, area of evaporation of dispersed material is expressed through the specific surface of evaporation [3]. Ostrikov A.N. and Shevtsov S. A. when drying crushed mushrooms in the form of a cube with superheated steam, the specific surface of layer a is determined by the formula [4]:

Δ ð ε ³

а= \ Í υµ k (1 - ε )^{2 ,}

where: a - specific surface of the layer, 1/m; Δp – hydraulic resistance of layer, Pa; ε – porosity of layer; Н l - height of layer of mushrooms, m; υ is speed of superheated steam, m/s; µ - dynamic viscosity of superheated steam, Pa·s; k 1 – constant of Kozeny-Pocket.

The authors [5, 6] carry out exclusion of a part of surface of particles touching and overlapping from the active heat and mass transfer by means of the coefficient of screening k s :

а′=а k s , (4)

where: а′ is the effective specific surface of material layer.

For particles in the form of a cube with a face size of 6 mm, the screening coefficient is assumed to be k s =0.93 [5]. However, it should be noted that the share of material surface involved in active heat and mass transfer may be less than 93 %, as can be seen from figure 1. In addition, the practical application of formula (3) is inconvenient due to large number of unknown components.

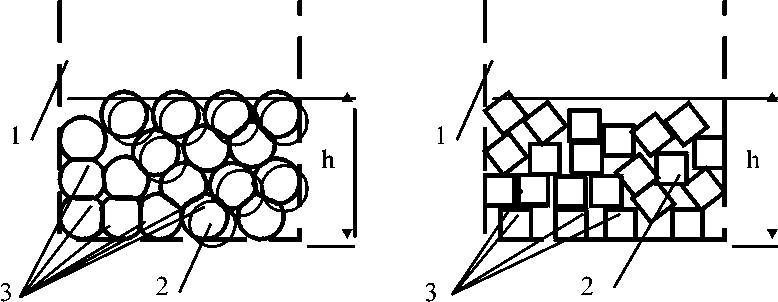
a)                                b)

a) – particles in shape of sphere; b) – particles in view cube.

1 - grid; 2 - particles; 3 - surface of particles non-used in heat exchange.

• Figure 1    – Scheme of disposition of particles in dense layer.

Lykov M.V. solved the problem of determining the surface of solid spherical particles with same diameter in a unit layer [7]:

6(1 - б)

5    ’

where: f - surface of solid spherical particles with same diameter per unit layer, m²/m³; δ –diameter of spherical particles, m.

Shumski K.P., Malkina A.I. and Maksimovskaya S.I. proposed applying a coefficient of surface efficiency of dried material m 1 for determination an active surface of heat and mass transfer, regardless of the form of particles at freeze-drying [8]:

f

mi = у, (6) fp where fa - area of actual or active surface of heat and mass transfer, m2; fp - area of the total surface of all particles, m2.

In turn, authors [8] calculate the f д from the ratio:

в_   f-в  fi

where: Pi is the coefficient of mass transfer for a layer of material with known surface of evaporation; Р’ - conditional coefficient of mass transfer, calculated on shelf surface; fl – known evaporation surface of material layer, m2; K –coefficient of shelf finned surface.

Connection of coefficient of shelf finned surface K with coefficient of surface efficiency of dried material m 1 :

ÊR

r m1= r Íd

here: R r – hydraulic radius; Н d – thickness of material deduced to a uniform layer.

The disadvantage of this technique is that the authors [8] in the formula (7) assume that for same drying mode, regardless of the loading rate, and, consequently, height of material layer, mass transfer coefficient remains constant. However, according to the literature data [9] it is known that, ceteris paribus, the value of mass transfer coefficient is affected by load rate of dried material. According to experimental data, it was found that at one drying mode, but at different heights of material layer, temperature of material has different values, and, consequently, different values of air moisture content on surface of material. In turn, the value of partial pressure of moisture vapor at surface of material determines the driving force of the drying process Δp, by which the mass transfer coefficient is calculated (formula 2).

It should be noted also that authors [8] give only theoretical calculations on coefficient of surface efficiency of dried material and do not give its numerical values, which indicates an incomplete study of this issue.

It is advisable to analyze coefficient of surface efficiency k f , with taking into account the intensity of drying process j . Coefficient of surface efficiency of dried material allows to take into account the real conditions of drying process. Thus, the entire surface of each material particle is involved in active heat and mass transfer [10]. And coefficient of surface efficiency of dried material, according to the formula (6), characterizes the ratio of the actual evaporation surface involved in the active heat and mass transfer to the total.

That is, if the actual evaporation surface of the material with a certain layer height at any drying mode is equal to:

W fa = -a, (9) j then the total or maximum evaporation surface will be calculated similarly:

W max

f max

j

In formulas (9) and (10) Wa, Wmax – amount of moisture removed from dried material, respectively, in real and ideal conditions; j – the intensity of drying.

Taking into account that these equations are characterized by same conditions of drying pro-cess, i.e. intensity of drying in both cases is same, then dividing the equation (9) by (10) we obtain:

f ^

aa f ^.

max     max

Knowing the value of coefficient of surface efficiency of dried material for a particular case, it is possible to determine the surface area involved in heat and mass transfer f д by the formula:

f a = k f ·f max ,                       (12)

and then calculate heat transfer coefficients by the formula (1), and mass transfer ones - by the formula (2).

Objects and methods of research

Experimental studies were conducted to determine meanings of coefficient of surface efficiency kf with the purpose of its analytical description. Experiments were carried out for dispersed materials of different geometric shapes (cube, parallelepiped and sphere). Investigations were conducted on the installation described earlier [11]. The installation is based on applying heat pump [12-14].

Topinambour tubers were used as studied materials in the form of a cube and a parallelepiped, and grains of green peas were studied as a material of spherical shape. The tubers of Jerusalem artichoke with initial moisture content (75÷77)% was milled to obtain particles in form of a cube with size of edges 5 mm and a parallelepiped with the dimensions of faces 9×3×3 mm. These sizes are adopted in accordance with the requirements of traditional drying technologies. The diameter of the grains was about 7 mm. Grain peas humidity was about 45%. The prepared material was placed with different height of bulk layer in pre-dried to a constant mass and weighted buckets with a diameter of 50 mm. Buckets are made from mesh with a cell diameter (0,7÷0,8) mm.

From 10 to 30 particles of the dried material were placed in the control bucket in such a way that they did not overlap and were at some distance from each other. This made it possible to ensure the contact of entire surface of particles with environment of the vacuum chamber. The resistance of the mesh walls was not taken into account. After weighing the particles in the control bucket, the average weight of one particle of the material Gp was determined. Then the number of particles in samples was determined:

n=G d /G p ,              (13)

where: G d - weight of sample.

Further, samples in buckets were placed in a vacuum chamber or a device for atmospheric heat drying, where they were dried. In the vacuum chamber, drying was carried out at medium heating temperatures up to 35, 46 and 60 ⁰C and pressures in the chamber 4, 6 and 8 kPa. Atmospheric drying took place at air velocities of 0.4 and 0.3 m/s, and air temperatures of 36, 38 and 40 ⁰C. Amount of removed moisture was determined at control intervals and the coefficient k f was calculated by the formula (11). The value of W max was calculated as follows:

W max = W p a n p ,            (14)

W p a =W c / n c ,             (15)

where W p a – average amount of removed moisture per particle of material in the control bucket; W c – amount of removed moisture from material in the control bucket; n c –number of particles in the control bucket; n p – number of particles in the test bucket.

Due to the fact that drying area of material involved in heat and mass transfer changes throughout the drying period, determination of amount of removed moisture was carried out every 30 minutes during the entire drying period. Correspondingly, calculation of coefficient of surface efficiency k f was conducted. Then arithmetic meaning of k f was calculated.

Results and discussion

Numerical values of the coefficient k f are given in table 1.

Table 1 – Magnitudes of coefficient of surface efficiency at drying of large-dispersed food materials

Layer height, m	topinambour		peas
	cube, 5 x 5 x 5 mm	parallelepiped 9 x 3 x 3 mm	sphere 0 7 mm
0.1	0.58	0.47	0.78
0.2	0.48	0.34	0.60
0.3	0.38	0.29	0.47
0.4	0.33	0.27	0.45

The results of experiments showed that in studied temperature and pressure ranges in vacuum drying chamber, the coefficient of surface efficiency does not depend on drying mode, but depends only on shape of particles of dried material and the height H of its bulk layer. Similar results were obtained in studied temperature and velocity ranges of drying agent in device for atmospheric thermal drying of thermolabile materials.

• Figure 2    shows the dependence of coefficient of surface efficiency of dried material on height of bulk layer of material. As can be seen from the figure, the dependence k f =f(h) for drying particles of different shapes has the form of a

expotentional function, which after mathematical processing was deduced to the form:

k_f = Ch - ^0.41 , (16)

where H –height of material layer, m; C -magnitude depending on the shape and type of material.

The highest kf values are observed in pea processing (figure 2). This indicates that in this case the area of solid particles of spherical shape is used to a greater extent. However, with increase in the height of the bulk layer of peas in the range (0.007÷0.021)m kf decreases sharply from 0.84 to 0.59. At a layer height more than 0.035 m kf virtually unchanged. Large values of kf are observed at drying topinambour with particles in the form of a cube. The lowest values of the coefficient of surface efficiency were obtained by drying particles in form of a parallelepiped. This indicates that in this case the particles overlap each other to a greater extent.

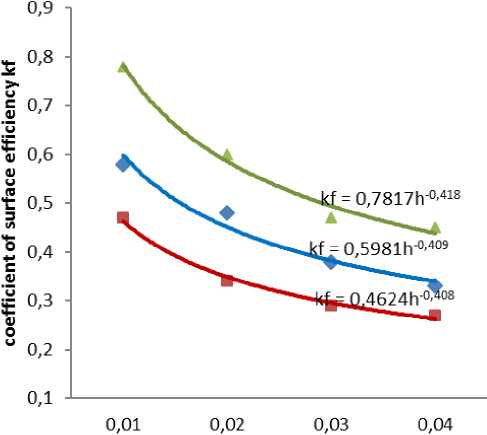
layer height h, m

• ♦ cube ■ parallelepiped A sphere

Figure 2 - Dependence of coefficient of surface efficiency of dried material on the height of the bulk layer.

Conclusions

The analytical description of vacuum and atmospheric drying processes of large-dispersed food materials located in a dense layer with different geometric shapes includes the coefficient of surface efficiency of the dried material. For this purpose, experimental studies on vacuum and atmospheric drying of large-dispersed food materials having the shape of a cube, a parallelepiped and a ball at height of the bulk layer of 0.01-0.04 m were carried out. Based on the analysis of experimental data, the empirical dependence is obtained, which allows with a sufficient degree of reliability to take into account the actual evaporation surface involved in active heat and mass transfer in the processes of vacuum-atmospheric drying of coarse food materials. Meanings of k f do not depend on type of drying (i.e., vacuum or atmospheric).