Determination of structural parameters of multilayer perceptron designed to estimate parameters of technical systems

Published Online October 2017 in MECS

One of the most significant spheres of the development of today’s technical systems for controlling and diagnosing of the objects of various designations is the improvement of the mathematical apparatus that is used for the estimation of the controlled parameters [2, 3, 8]. It is believed that the large perspectives of such the improvement are related to the use of the neuro-network models (NNM) [1,  6]. Prerequisite of the use is established NNM’s ability to solve effectively weakly formalized problems. This, in addition to the rest of the facts, allows significant simplification and shortening of the process of the development of mentioned controlling and diagnosing systems. Although, rather a large number of various NNM types are currently in use, multilayer Perceptron (MLP) is used commonly as basic model. For instance, MLP lies in the basis of deep neuron networks used by Google and Facebook companies for the recognition of both voice signals and pictures. In addition to this, the mentioned NNM type unambiguously demonstrates its prospects for estimation of controlled parameters for:

• 1.    Cyber-attacks recognition;

• 2.    Voice signals;

• 3.    Technical conditions of building constructions [1-4].

At the same time, practical experience of using of the neuro-network recognition systems as well as results of the researches [2, 3, 7] shows that it is necessary to increase efficiency of MLP application. This goal can be reached by adaptation of MLP structure to the problem specifications set. This statement is based on the fact that the MLP structure influences significantly its generalization error. In its turn, the application efficiency principally depends generalization error.

• II.    Analisys of existing publications

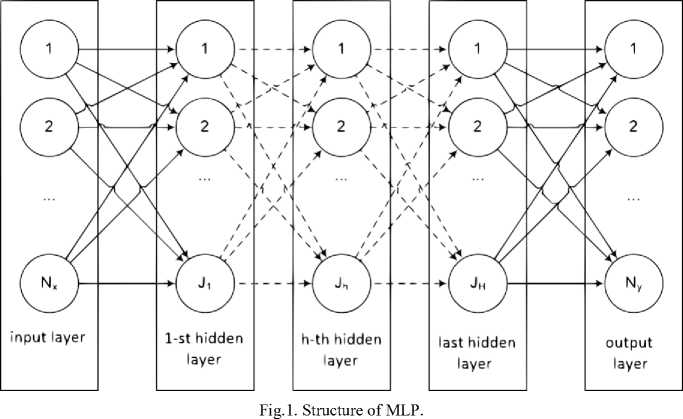
Generally, MLP (shown on Fig. 1) corresponds to neuro-network that consists of a number of layers. Each layer, in its turn, consists of artificial neurons that are connected in series [4, 5].

We should note that in case of MLP shown on Fig. 1 numbers of input and output neurons equals to N and N , number of hidden neurons equals to H , and numbers of those in the first, h -th and the last hidden layers are J , J and J , respectively. We are going to consider classic MLP that has no inverse links. In this model, each neuron within the hidden layer receives all the output signals from the preceding layer, and its output signal can be transmitted to any neuron belonging to the next layer. Linear activation function is used for the neurons within the input and output layers. Within the hidden neurons logistic sigmoidal function is used.

Lw max ,

Principal parameters to define MLP structure are number of the input neurons, number of hidden layers of neurons, number of neurons within each hidden layer and number of output neurons.

Based on the results of [1, 4, 7] we can suppose within the first approximation that the number of input and output neurons corresponds to the number of the parameters being registered as well as the number of the objects recognized. These values are specified a priori. They are based upon the problem specifications set and are not subject to any change. Therefore, MLP structure can be optimized but at the expense of the number of the hidden layers of neurons as well as the number of the hidden neurons within each of the layers. The following calculation expressions are submitted in [1, 3]:

< P X E

N y x P            ( p A

—-----< L <  N_ x I-- + 1 I x

1 + log2 P w    x  I N x   J

where N_x , N_y are the numbers of input and output neurons;

L is the number of synaptic bonds;

P is the number of the training examples;

^ max is the maximum allowable recognition error.

But practical experience and results [5] shows that the available solutions of (1-3) require significant improvements.

It is reasonable to highlight papers [1, 4] in which some expressions were derived for the determination of optimum number of hidden neurons for the two-layered perceptron:

x ( N x +N y + 1 ) +N x

PP

,(2)

x     y     w          xy

,

( 0,4 N X + 0,2 ) x

N o ^pt ( min ) = Round

x JPNL- l Nx+Ny  J

,

(

N Opt ( max ) = Round •

2 JPN X )

Ny

V      Y J

G MLP ^ ^min,

where N O ^pt ( max ) and N Opt ( min ) are maximum and minimum boundary values of the optimum number of hidden neurons;

Round(X) is the operation for the determination of the nearest integer number derived of argument P .

Use of (4, 5) restrict the search area of the optimum number of the hidden neurons, but the area of use of these two expressions is limited by two-layered Perceptron. Besides to this, additional limitations are imposed to it with the following prerequisite:

P >  10 N x .                  (6)

The prerequisite has too general nature and does not take into account the amount of the classes for recognition, that should be represented in the training sample.

We shall note as well that many papers denoted to the MLP application for the estimation of the parameters of the technical systems do not contain substantiated method of calculation of its structural parameters. Even approaches for the determination of the best parameters of the MLP structures contain some contradictions. Thus, they use principle of minimization of synaptic bonds in [1] which are necessary for the network training on the specified set of examples in [1]. But the specified principles contradict [7] where they suggest that the reduction of the network size does not lead to the increase of its generalization possibilities.

At the same time, general specific feature of the papers that have been analyzed is the fact that the main conditions of problem domain that influences MLP’s structure are:

• 1.    The number of input and output parameters;

• 2.    The amount of training sample;

• 3.    The maximum allowable recognition error.

So, the purpose of this research is to develop a procedure for the determination of the MLP structure parameters and determination of the number of these parameters.

where G_MLP is the relative MLP error.

In terms of the paper, the term, relative MLP error means division of generalization error ( ε ) means by the number of synaptic links ( L_w ):

G MLP

ε

. L w

We should note that the generalization error of the neuro-network corresponds to the error of the recognition of the parameters which were not used for the MLP training. In other words, this is the error of the recognition of the parameters which are not constituent part of the training, test, or validation samples. Rewriting (7) taking into account (8) we obtain the following:

— ^ min.             (9)

L w

We should note that for the full-linked MLP the following is true:

^Lw = ^Nx ^X J 1 ^+J1 ^X J 2 + ... +

.   (10)

+ J h - 1 ^{X J}h + ... +J H - 1 ^X J H +J H ^{X N}y

In case, when number of neurons in each of the hidden layers is the same, it is possible to transform (10) as follows:

L w = ( H - 1 ) x J ² + ( N x +N y ) x J ,     (11)

where J is the number of neurons in a hidden layer;

H is the number of hidden layers of neurons.

Taking into account the results of [1, 4] we should suppose that when solving (9), it is possible to state that the generalization error and the number of synaptic links are continuous quantities. The assumption allows determining of optimum number of synaptic links ( L^o_w^pt ) basing upon the solution of the following equation:

III. Development of the Mathematical Apparatus

According to [3, 6] development of the MLP structural model is based on the determination of the total number of synaptic links. We are going to take minimization of the minimum relative MLP error criterion as base of this determination according to [6, 7]:

According to [3, 6] development of the structural MLP model is based on the determination of the total number of synaptic links.

^ L w = 0. d £

Let us detail constituent equation (12). Generalization error is calculated as sum of the approximation error ( ε a ) and model description error ( ε o )

ε=ε_а +ε_o .

We should mention that the approximation error relates to the memorizing of the training data by MLP, but description one relates to the generalization of these data.

According to [1, 7] we can assume that the approximation error is proportional to the ratio of the sum of input and output neurons and number of synaptic links:

N +N xy ε_a

Lw

.

Error of the model description is calculated as follows:

ε

L w ~

P

where P is the number of training examples.

Upon substitution of (14, 15) in (13) we derive the following:

ε ~

Г N x +N y

V   L w

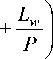
Substituting (16) in (12) we can derive the following upon conducting trivial conversions:

under equal calculation possibilities number of synaptic links of MLP is somewhat lower than the synaptic bonds of the two-layered perceptron. It allows assuming of the following in the first approximation:

L d = L w ,                  (20)

where L_d is the number of synaptic links of the twolayered perceptron.

The number of the synaptic bonds of the two-layered perceptron is determined as follows:

L d - ( N x +N y ) x N 1 ,           (21)

where N ₁ is the number of the hidden neurons within the two-layered perceptron.

Taking (20, 21) into account we can rewrite expression (19) as follows:

( N x +N y ) x N pt - k^P x ( N x +N y ) - 0 ,  (22)

L P ~ J P x ( N x +N y ) ,         (17)

where L^o_w^pt is optimum number of synaptic bonds of MLP.

Taking into account (11) we can put down proportion (17) in the following form:

[ ( H op - 1 ) x J   + ( N x + N y ) x J^¹ ^ ~

,     (18)

~ 7 P x ( N x +N y )

where J ^opt is optimum number of neurons within a single hidden layer;

H ^opt is optimum number of the hidden layers of neurons.

Introduction of the proportionality factor allows writing (18) in the form of the following quadratic equation:

[ ( H op - 1 ) x J^ oPt + ( N x + N y ) x J° ° ^p ^ -

,   (19)

• - k^P x ( N x +N y ) - 0

where k is some proportionally factor.

We should note that the solution of equation (19) foresees determination of the two unknown values of J _w^opt and H ^opt . In addition to this, we shall estimate the magnitude of k factor preliminarily.

Let us make use of expression [4] which suggests that where N opt is the optimum number of the hidden neurons within the two-layered perceptron.

Determination of optimum number of the hidden neurons is reduced to the following calculation:

N opt -k x

V P x⁽ N x +N y ) ( N x +N y )

We are going to use Hecht-Nilsen theorem for the determination of factor for which it was proved that minimum number of neurons equals to:

N min >  2 N X + 1.             (24)

We, too, shall take into account that maximum number of hidden neurons should not exceed the number of the training examples:

N max <  P .                (25)

Equating (23) with (24) and (23) with (25) we derive the following:

7 P x⁽ N x + N y )

k x —₇-------r— >  2 x N у + 1,

( N x + N y )         X

k x V ^{P x}( N X + N Y ) <  P . _     ( N x + N y )

As the consequence, we are going to take into consideration specifics of the actual problems related to the evaluation of the parameters of the technical systems for more exact determination of the factor. As a rule, in these problems:

• 1.    The number of the output parameters does not exceed the number of the input ones;

• 2.    The output neuron corresponds to each recognition class;

• 3.    The number of the training examples for each recognition class should exceed the number of the input parameters at least 10 times;

• 4.    Total amount of all the training examples should exceed the number of the recognized classes at least 10 times as well.

Therefore, we can assume the following without infringing inequality (26):

P = 10 X N = 10 x10 X N = 102 X N .(27)

yxx

We are going to derive the following upon substitution of (27) in (26):

Ik > «^NX?^, .(28)

V Nx x( Nx+N, ).

k <  10 X N N _X x ( N_x+N , ) .

We can assume the following in case of rather great number of input parameters:

2xNx +1 = 2xNx .(29)

This allows reduction of (28) as follows:

k >  0,2 x .N x x ( N x + N , ) ,

-                                     .

_ k <  10 X V N x x ( N x + N , ) .

Substituting (30) in (23) we can rewrite expressions for the evaluation of the range of optimum number of the hidden neurons of the two-layered perceptron in the following form:

N 0 ^pt( min ) = 0,2 x N x x ( N X + N , ) x

.      (31)

7 ^P X^{( N}x^+Ny )

^X   ( N x +N y )

N 0 ^pt( max ) = 10 x N_x x ( N X + N , ) x ,      (32)

У P X⁽ N x +N y )

^X   ( N x +N y )

where  N°pt(max) ,  N°pt (min)  are maximum and minimum boundaries of the range of optimum number of hidden neurons in the hidden perceptron.

Upon appropriate reductions and taking into account that the number of the hidden neurons should be integer number we can finally derive the following equation for the two-layered perceptron:

N 0p ( min ) = Round ( 0,2 x ^ N_x x P ) .     (33)

N 0 ^pt( max ) = Round ( 10 x ^ N_x x P ) .     (34)

Use of expressions (11, 20, 21, 33, 34) allows rewriting equations for the determination of optimum MLP structure in the following form:

( Я min - 1 ) x J”“² + ( N x +N y ) x JT =

,      (35)

= ( N_x +N_y ) x Round ( 0,2 x ^N_x x P )

( H max - 1 ) x J max + ( N x + N y ) x J^^x =

,     (36)

= ( N_x +N_y ) x Round ( 20 x ^N_x x P )

where H ^min , H ^max are minimum and maximum number of the hidden layers of neurons within MLP;

J ^min , J ^max are minimum and maximum number of neurons within single hidden layer.

Further refinement of the number of hidden neurons within the limit from H ^min to H ^max is recommended to do by conducting of numerical experiments related to minimization of the approximation error. We should note that the determination of optimum ratio of the number of hidden layers and the number of neurons within the single hidden layer requires further studies.

Let us consider change of the search range of optimum number of hidden neurons of the two-layered perceptron when using the model developed in order to estimate information value of the results obtained. We shall evaluate change of the range with the help of the following expression:

_d_ N ^Pt ^ max ^ - N oPt ^ min ) N max - N [min

Let us consider the problem that is related to the evaluation of the parameters of computer systems for the purpose of revelation of cyber-attacks. We are going to take into account that the number of the input parameters is ca. 100 ( Nx «100 ) f°r the majority °f similar problems, but the number of the training examples required for the effective training of MLP equals to 20,000 (P « 20,000). We assume that we apply a tw°-layered perceptron with a single output (Ny = 1 ). If we use the mentioned parameters in expressions (33, 34) we derive the following: N1min =282 , N1max =14140 . Using these results in (37) we derive that δ ≈ 0.7 . Therefore, range of search of optimum number of hidden neurons narrowed nearly 1.5 times.

Perspectives of the further studies are related to the improvement of the architectural parameters of MLP. First of all, it is reasonable to the development the detailed method for the adaptation of the number of hidden layers to the applied problem specifications set.

• IV. Conclusions

It was shown that increasing efficiency of the multilayer Perceptron application for the estimation of the parameters of the technical systems is possible at the expense of the adaptation of its structural parameters to the problem specifications set. It was proposed to conduct adaptation from the positions of minimization of the relative error of the neuro-network model. Mathematical apparatus was developed which allows calculation of the most acceptable range of the number of neurons within the hidden layers.