Determining the Number of Effective Distributions Based on Neural Network Ensemble

Today, storing, processing, and analyzing big data streams is one of the most urgent issues in the field of computer technology [1, 2]. Although extracting results from big data streams requires complex processes, the fact that these data streams contain valuable hidden meanings has led to continued research on them [3, 4].

It is known that processing large data streams requires the use of specific special algorithms. The use of special algorithmic tools in data stream management allows for fast and high-quality data processing. Traditional methods for fast processing of large data do not show effective results [5-7]. Today, the use of distributed methods for fast and high-quality processing of large data is considered to be purposeful [8, 9]. In general, several servers are needed to organize distributed computing systems. However, it is possible to apply this mechanism to a single-server database [10, 11]. For this, the tables of the database contained in a single server can be used as distributed systems [12, 13]. As a result, storing and processing data based on distributed tables leads to effective results. In this case, that is, when applying distribution mechanisms to database tables, the main issue is to develop a data management algorithm based on internal distribution. A special module for managing data streams in tables created based on the internal distribution mechanism will need to be developed. This module can be organized as a set of modules that perform two interrelated functions. The first module performs the task of distributing tables according to the characteristics of data flows and computing machines, organizing the overall structure [14, 15]. The second module processes the data stored in the selected tables, and correctly organizes the queries submitted to it [16]. The first module performs complex processes in managing data flows. One of these processes is determining the number of effective distributions. As mentioned above, distributed processing of data leads to time efficiency. However, excessive distribution leads to an increase in the time of processes related to data distribution and has a negative impact on the overall time efficiency. Or, if a sufficient number of distributions is not implemented, the maximum efficiency expected cannot be achieved with a small number of distributions. This situation can be interpreted as an analogy of having more people working on a small problem than necessary or having too few workers on a very large problem. In short, determining the number of distributions appropriate to the situation is one of the important problems in research on distributed systems [17]. Since this process depends on a number of factors, it is advisable to automate it using intelligent systems. The solution to this problem will be considered during this resaerch work.

2.    Method and Materials 2.1.    Research Methodology

Data flow management based on the application of distribution mechanisms to database tables depends on the number of distributed tables. Therefore, the object of this study is to determine the number of distributions required for the system to operate in the most efficient way. This goal is achieved based on the following methodology (Fig. 1).

Determining the effective number of distributions

Preparing datasets for Al algorithms

v

Training and testing Al algorithms

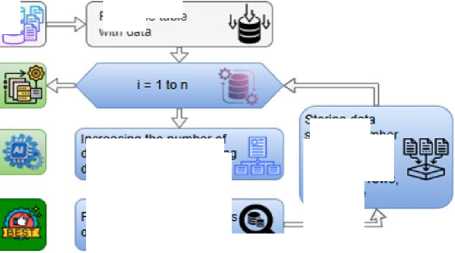
Filling the table with data

Performing various q on distributed tables

Increasing the number of distribution and distributing data into it

Fig.1. Methodology for intelligently determining the number of effective distributions

Create a database „ and forming tables in it

Storing data such as number of distributions, data size, number of rows, query time

The number of distributions is determined by the system's ability to respond quickly to requests. In other words, the number of distributions and the time of the request are closely related to each other. Therefore, in the research methodology, after creating a database and filling the necessary tables with data, the number of distributions and the time spent on the corresponding requests are determined on a cycle-by-cycle basis. Then, based on the data collected during the cycle, artificial intelligence algorithms determine the optimal number of distributions. The processes reflected in this research methodology are covered in detail during the study.

• 2.2.    Formation of Preliminary Data for the Development of Distribution Rules

Based on the developed research methodology, some experimental queries were performed on specially distributed tables of the database. A table with 10,853,312 rows of records stored in the database of a single computer server was used for the experimental tests. The experiments on the selected tables are mainly carried out in the following order.

• •    In the first experimental tests, separate search queries are performed on the table with 10,853,312 rows of records (Table 1).

• •    In the next experimental test, the 10,853,312 tables are divided into 1,2,3,5,7,10 distributed tables based on a certain established rule. In the next step, search queries are performed separately in each group of distributed tables, as in the first experiment. The results of the experimental tests can be seen in Table 1.

• •    In this step, the first and second experimental tests are performed in the query streams. That is, queries are made to the selected table or set of tables simultaneously by several computers (Table 2).

• 2.3.    Development of Machine Learning-based algorithms to Determine the Number of Effective Distributions

Table 1. Query time metrics for various distributed tables

Number of distributions	Average number of records in a single table	Average time taken for a query
1	10 853 312	7.3912
2	10 853 312/2	3.5083
3	10 853 312/3	3.0222
5	10 853 312/5	1.8281
7	10 853 312/7	1.6150
10	10 853 312/10	0.0073

Table 2. Time metrics for querying distributed tables in a stream by multiple users at the same time.

Number of distributions	2	3	5	7	10
Query sending time (seconds)	955	453	344	145	80
Number of queries in the stream	468	586	678	251	2430
Number of queries per second	0.49	1.29	1.97	1.73	30.37
Average time taken for a single query per stream (seconds)	12,7761	4.1783	3.0746	2.8973	0.0077

According to Table 1 above, when a table with an average of 10 million records is divided into 5, 7, and 10 tables, the query time decreases to 1.8, 1.6, and 0.007 seconds, which is quite efficient. Table 2 shows that even though the number of queries in the form of streams increases, the average query time decreases due to the increase in the number of partitions.

It can be seen from the above tables that the use of distributed methods on a single server leads to improved time efficiency even when the size of data and streams increases. However, this is not enough, because the highest efficiency is achieved when the optimal number of tables (x) is determined to process a query on a table with n records in m seconds. The most efficient approach to determining x is to use artificial intelligence models. Therefore, the next steps of the research will focus on finding a solution to the problem based on artificial intelligent algorithms.

Determining the number of database table distributions based on experience is not always an effective approach. In addition, the number of distributions also depends on the characteristics of the servers. The number of distributions determined for a particular computing machine may not be suitable for a computing machine with other characteristics. In such cases, one of the effective methods for determining the number of distributed tables based on the specified characteristics is the use of artificial intelligence and machine learning approaches. To determine the number of distributed tables, a data set was initially formed for training and testing machine learning algorithms. Based on correlation analysis, scaling, normalization, and encoding methods, the data set was prepared for machine learning models [18-21]. In this case, the method of determining Pearson correlation coefficients is used to extract the desired features from the data set (1).

_       k-£uv-£u-£v

here r_uv - correlation coefficient of u value and v value, k - number of observations, £ u- sum of u sets, £ v- sum of v sets, £uv - sum of the product of u and v sets, £ u ² - sum of squares of u set, £ v ² - sum of squares of v set [22]. As a result, the following features were found to be the most important in the data set:

• •    the volume of data to be processed;

• •    the number of records in the database under consideration;

• •    the number of table partitions;

• • the time spent on processing data in distributed tables.

In addition, in data preprocessing step all the data had been scaled by minmax scaling method (2):

_ ^ui.j ^u jmin

Ulinew   ujminjmax here Uij - the value at the intersection of i - row and j - column, Ujmln is the minimum value in column j, Ujmax is the maximum value in column j [23].

Also, one hot encoding method was used to convert textual data in the dataset into digital form [23].

In the research work, the following artificial intelligence algorithms were used to intellectualize the need to divide a query to a table with n records into x tables in order to process it in m seconds:

Random Forest, XGBoost, Support Vector Regression, Multiple Linear Regression.

The general steps of the algorithms based on these artificial intelligence models are performed in the following steps.

Step 1. Start;

Step 2. Receive the data set;

Step 3. Prepare the data set;

Step 4. Calculate the correlation coefficients of the fields;

Step 5. Split the data set into test and training sets;

Step 6. Train the machine learning model;

Step 7. Test the machine learning model;

Step 8. Model evaluation (RMSE, MAE);

Step 9. If (RMSE < 2 and MAE < 0.80) then go to step 10;

otherwise go to step 6;

Step 10. Accept new data for distribution;

Step 11. Train the new data to the Machine Learning model;

Step 12. Determine the distribution boundaries based on the prediction;

Step 13. Print the result;

Step 14. Done.

It is known that Random Forest, XGBoost, Support Vector Regression, Multiple Linear Regression algorithms are traditional algorithms of artificial intelligence, and there are several shortcomings in their use. These problems include [24-26]:

• •    adaptation of models to the training sets;

• •    drift of prediction results from extreme values;

• •    emergence of instability in models.

• 2.4.    Development of a Neural Network Ensemble Method Based on Machine Learning Algorithms to Determine the Number of Effective Distributions

To prevent drift of prediction results from extreme values, instability of models or adaptation to sets, it is necessary to smooth the results obtained from the most effective machine learning ensemble models. Therefore, in order to increase the accuracy during the study, a Neural Network Ensemble is used.

To intellectualize the process of distributing big data streams, it is desirable to generalize machine learning ensembles based on neural networks. In this case, the prediction results are smoothed to obtain results based on the best algorithms. The study developed a method for smoothing the prediction results and generalizing the metadata generated from them based on neural networks by training several machine learning algorithms together and combining their strengths. The developed method is based on modern ensemble approaches, which combine the results of each model using the strengths of Random Forest, XGBoost, Support Vector Regression and Multiple Linear Regression algorithms [27]. This data is transmitted to a multilayer perceptron neural network, which is a meta-model, and the results are obtained. The processed data set is presented in the form of the following set:

D = {(X^y^                                (3)

Where X_t is the feature vector, y _t is the target values, N is the number of samples. In this case, the training data set is divided into two parts. D_t = {(x_i,y_i)}^₁ is for training the base models, D_m = {(X j ,y j )}j^._{N +1} is for training the Metamodel.

The set of base models that combines the strengths of machine learning is defined as below (4).

^M = ^{f RF i^f XGB i^f SVR i^f lR }                                         ⁽⁴⁾

For each model, f_k E M,k E {RF,XGB, SVR, LR] are satisfied and these models are trained on the D_t data. This set of models is used to generate input data for the neural network meta-model. Each model is trained separately and given prediction values on the test set. These predictions are then combined as a feature vector in formula (6) and fed to the meta-model. The generation of predictions of the main models is done on the D_m data and is expressed by (5).

y^_k = Mfi VX j E D m , Vf_k E M                               (5)

To combine the strengths of the models used to smooth the prediction results, the input data for the Meta-model are created. To do this, the predictions of the main models are combined, and for each j -sample, a new feature vector of the form (6) is created:

^Z j — [V rf ’У хсв ’У $ук ’У ьк]                                            (6)

The vector (4) above constitutes the input data for the meta-model. Each sample Z j and the corresponding true target value y j are combined and expressed by (7).

	Z j — {(Z j ,y j )} j=i	(7)
As a result, the new metadata set is rep	resented as follows (8): C (1  .nW  nW   nW  v 1 y RF    y XGB   y SVR    y LR    y 1 - (2)    ^(2)     ^(2)     ~(2)
Z j —	y RF   y XcB  «WR   « LR    У 2 :                    :                    :                    :                 : k'1 «S ’ y^R у !?’ у » , ]	(8)

Formula (8) represents the dataset created for training the meta-model (i.e., the neural network). In each sample (i.e., each j) — the predictions given by the main models (e.g., RF, XGBoost, SVR) in the study are combined and they are paired with the actual results. A multilayer perceptron (MLP) neural network is used as the meta-model. The meta-model aims to combine the strengths of the underlying models and smooth their predictions to approximatey j . To optimize this process, the following objective function is formulated (7):

minL(g(Z;0’,y)                                       (9)

e

Here, 0 is the training parameters (coefficients and biases) of the MLP model, g(Z;0~) is a function representing the output of the neural network. The main task of the neural network used as a meta-model is to maximize the accuracy of the final result by combining the predictions of the main machine learning models. To do this, the neural network is based on a loss function that measures the difference between the predictions given by the models and the actual target values. This means that the parameters of the meta-model (i.e. the weights and biases in the neural network) should be chosen in such a way that the amount of loss (error) between the predictions and the actual values for all training samples is minimal. The reason why minimization is necessary is that this way the model makes fewer errors in its predictions, i.e. the predictions are as close as possible to the actual values. In this way, the neural network not only combines the main models, but also balances their individual weaknesses and, as a result, improves the generalization ability. The minimization process is carried out using gradient-based optimization methods (e.g. SGD, Adam). L is the loss function, and its general form is given in the following form (10).

» m

A neural network consists of several layers, each layer processing input data and generating output. This is represented as a C -layer neural network as follows (11).

д(^У 0) — h(c) c — 1.....C, h(c) — a(W(c^h(c-1’ + й(с))(11)

Here 0 — {Ж ^(с) ,Ь ^(с) } ^С - ₁ - is the training weights (№ ^c) ) and biases (i ^(c) ). The final prediction function of the neural network is expressed by (12).

у(П — g(Z(j\0)(12)

When applying the neural network composite regression method on the test data, the test data is defined by D_s — {(^ fc ’} » =i, and the predictions y _te — f_k(x_k) ^f_k £ M_t , ^x:_k £ D_s are obtained from the base models for the test data. Based on the combination of the strengths of the base models, test metadata is created to smooth the predictions and is expressed by (13).

^Z s ^— {^RF^XGB^SVR^LRy }                                  ⁽¹³⁾

The final predictions are calculated using the Meta-model to perform prediction smoothing based on combining the strengths of the underlying models and are expressed by (14).

У — g(Z_s)                                             (14)

Formula (14) represents the function of providing the final prediction by the meta-model. That is, the predictions given by the main models in the previous stage are passed to the neural network. The neural network, based on its trained parameters, provides the final value for each sample in the form of y . In this process, the MLP learns how to combine the weights between the main models, and outputs the result in the form of a smoothed, optimal prediction.

The regularization method is also used to optimize the applied neural network model. This process describes the neural network regression method. The selection of the main and meta-models and the optimization of their parameters have a significant impact on the result.

The main reason for choosing algorithms such as Random Forest, XGBoost, and Support Vector Regression (SVR) in this study is their high accuracy and flexibility in solving complex regression problems:

Random Forest is based on an ensemble of multiple decision trees and is resistant to the problem of overfitting, has high accuracy and stability [28].

XGBoost is a powerful algorithm based on gradient boosting, which is used at the industrial level in terms of accuracy and speed, and is especially effective in studying complex relationships.

Support Vector Regression allows for high-precision modeling of linear and nonlinear regressions and works especially well on smaller training sets [29].

When these models are used together, their individual strengths — stability (Random Forest), accuracy and speed (XGBoost), and smoothness and generalization ability (SVR) — are combined. This significantly increases the overall accuracy and robustness of the final model.

3.    Results

To intellectualize the need to divide a query to a developed table with n records into x tables in order to process it in m seconds, experimental results were obtained on machine learning algorithms based on Random Forest, XGBoost, Support Vector Regression, and Multiple Linear Regression methods. The experimental results are presented in Table 3.

Table 3. Machine learning algorithms used to partition database tables based on data training and their effectiveness

Algorithms based on Machine learning	RMSE	MAE
Algorithm based on the Random Forest model	1.64	0.96
Algorithm based on the XGBost model	1.73	0.88
Algorithm based on the Support Vector Regression	1.65	1.05
Algorithm based on Multiple Linear Regression	1.71	1.008

As a result of data training, the algorithm based on the Random Forest model of machine learning, which was used to divide the tables in the database, recorded the most effective results in terms of RMSE of 1.64. Using the Random Forest model of machine learning, it was determined how many tables should be divided into to process the table data in a database with 10,853,312 records in 2.31 seconds, and as a result, the Random Forest model-based algorithm responded that it was necessary to divide it into 4.48, that is, 5 tables.

The developed neural network regression method is designed to work with complex and large data. The method mainly allows you to train a combination of Random Forest, XGBoost, Support Vector Regressor, and Multiple Linear Regression models together through linear and nonlinear relationships and creates the possibility of smoothing the prediction results, which significantly increases the accuracy of the model. Experimental results were obtained based on the neural network method to intellectualize the need to divide data in a table with n records into x tables in order to process them in m seconds. The accuracy of the method based on the experiment is presented in Table 4.

Table 4. Results of the neural network ensemble method for determining the number of effective distributions

	RMSE	MAE
The neural network ensemble	1.642	0.862

Table 5. Advantages of the proposed method

№	Main theoretical advantage	The proposed method	Traditional methods (RF, XGBoost, SVR, LR)
1	Balancing bias and variance	Reduces model deviation and increases accuracy through smoothing	Relies on a single model, variance or bias may be high
2	Studying nonlinear relationships	It studies any nonlinear relationship (universal approximator)	Most of them depend on linear or finite kernel functions.
3	Ensemble advantage -generalization through stacking	Each model combines its strengths, smoothed by a metamodel	Each model works separately, the combination is limited
4	High parameter flexibility and scalability	Flexible with dropout, normalization, and regularization	Model parameters are limited, difficult to scale

It can be seen from Table 4 that the performance of the proposed approach is slightly improved over the results of traditional machine learning algorithms. Although the performance has a small change, this method can be used as a reliable model because it overcomes the shortcomings of traditional approaches.

4.    Conclusions

In conclusion, the proposed artificial intelligence model has several advantages, as can be seen from the comparison results presented in Table 5.

In general, the research work is devoted to one of the problems encountered in managing big data streams based on the internal distribution mechanism. In other words, the study investigated the issue of finding the optimal number of distributions for efficient storage and processing of big data streams. First of all, the research methodology was covered. In the next steps, the number of effective distributions was determined based on the data collected on the basis of experiments using the Random Forest, XGBoost, Support Vector Regression, and Multivariate Linear Regression machine learning algorithms. As a result of these experiments, the algorithm based on the XGBoost model recorded the best result (0.88) in terms of the MAE evaluation indicator. In general, this result could also satisfy the study, but since traditional machine learning models have problems such as adaptation to the training set, deviation of prediction results from extreme values, and the appearance of instability in the models, a new method was developed for the study. The neural network ensemble method developed in the study solved the above problems, and the error rates were reduced compared to previous methods. That is, the neural network ensemble method achieved values of 1.642 in terms of RMSE evaluation indicator and 0.862 in terms of MAE evaluation indicator.