Determining the Optimum Time Quantum Value in Round Robin Process Scheduling Method

Published Online September 2012 in MECS DOI: 10.5815/ijitcs.2012.10.08

The operating system (OS), as the most important program needed for starting up and using the hardware, has different managing tasks each of which, is performed by one of the management units of the OS. The process management, as one of these management units, allocates the processor to the processes using several allocating algorithms.

One of the most common algorithms in processor allocation, is the Round Robin (RR) algorithm in which, the ready processes waiting in ready queue, are dispatched sequentially and allocate the processor for certain period of time known as time quantum (q) or time slice. If a process is finished during its time quantum, releases the processor, otherwise the processor is pre-empted by the OS and is allocated to the next ready process waiting in front of the ready queue and the current process will be moved toe the end of the this queue. The algorithm continues until all the processes are terminated, or the system is switched off. This method is known as best dispatching algorithm in time sharing systems [1].

The most important issue in RR algorithm, which highly affects its efficiency, is determining the amount of the time quantum. Assigning very small and very large values for this parameter, will lead to performance decrease due to increasing context switching overhead, and degradation of the RR method to FCFS algorithm consequently. Actually the value of the quantum parameter is selected in 10-100 milliseconds range [2]. Each value will lead to a specific performance and will affect the algorithm's efficiency by affecting the processes' waiting time.

In this research, a mathematical model is developed to obtain the optimum value for time quantum parameter in order to minimize the average waiting time of the processes. The model is implemented in Lingo software and solved for four selected problems from the literature.

The content of the paper is organized as the follows: The problem definition and the literature review is discussed in section 2. The proposed mathematical model is completely discussed in section 3. Section 4 contains the implementation and computational results of the proposed model over four adopted problems from the literature. Conclusions are summarized in section 5.

• II.    Literature Review
  
  2.1    Terminology

This research is related to one of the most important issues in principles of the operating system design. In This section, the more frequently used terms in this literature are defined. Some of these terms, are used as the efficiency criteria by some researchers [1], [2].

• ■    Process: The program which is loaded into memory to be executed.

• ■    Ready Queue: A waiting list holding ready processes according to incoming order. These processes are waiting for dispatch.

• ■    Scheduling: Making decision about allocating policies of the recourses to the processes.

• ■    Long-term Scheduling: Making decision weather to accept a new job or not.

• ■    Short-term Scheduling: Also known as dispatching, deals with the allocation or releasing the processor to the ready processes.

• ■    Non pre-emptive Scheduling: A scheduling policy in which, the processor will not pre-empted by the OS after allocation.

• ■    Pre-emptive Scheduling: A scheduling policy in which, the processor can be pre-empted before the process is terminated normally.

• ■    Time Quantum: Also known as time slice, the amount of time that a process captures the processor.

• ■    Process State: The current situation of the a process in the system, including ready, waited(blocked), running, suspended, etc.

• ■    Waiting time: A time period which a processes waits to allocate a resource in the system.

• ■    Burst time: A time period which a process needs for completion.

• ■    Context Switching: Switching the processor from the current process to next ready, includes storing and retrieving the values of flags and some important registers.

• ■    Turnaround Time: The time interval between dispatching and completing of a job.

• ■    Response Rime: The time taken until the first response of a typical request is emerged.

• ■    Throughput: The number of completed(finished) jobs in a specific time period.

• 2.2    Round Robin Scheduling

The main goal of the CPU scheduling is distribution of the CPU time among the ready processes in a way that at least one of the system efficiency criteria is achieved. These criteria can be listed as below: [2]

• ■    Acceptable response time.

• ■    Performing the task (process) during the user predefined time period.

• ■    Increasing the CPU utilization.

• ■    Increasing the utilization of other system resources.

• ■    Decreasing overall overhead.

• ■    Decreasing the user waiting time.

• ■    Decreasing turnaround time.

• ■    Increasing the system throughput.

• 2.3    Previous Works

Some of the mentioned criteria are related together and will be affected by changing the others. Besides, these changes may not be at the same direction. That is, optimizing one of them, may lead to worst values for another and a unique optimum solution satisfying all these criteria ate the same time does no exist necessarily [1,2].

The scheduling algorithms can be divided into two types, pre-emptive an non pre-emptive. The former type methods, allocate the processor to the processes exclusively until completion. The latter type methods, pre-empt the processor from the process at a specific time slice before completion and switch to the next processes.

Round Robin is one the pre-emptive short-term scheduling policies in which, each of the ready processes waiting in the ready queue, get a time slice known as quantum to allocate the processor. If the amount of this quantum is enough for completion of the process, the process will release all allocated resources after termination, otherwise, the operating system re-takes the processor, and the process moves to the end of the ready queue to get dispatched again. So, a context switching occurs and the next ready process allocates the processor for the same quantum of time.

The most important parameter in this scheduling algorithm, is the amount of the time quantum [1]. If a small value is assigned to this parameter, the short processes will pass the system very soon, and the overhead of the system will increase due to the increasing the number of context switches. On the other hand, if the amount of the time quantum is larger than the maximum burst time of the ready processes, this policy will downgrade to FCFS scheduling algorithm. The value of this parameter at least should be considered as a little more than a specific transaction [2], or the time needed for a common conversation [1].

It's obvious that the amount of this parameter, highly affects the value of waiting time, turnaround time and response time of all the processes, and the number of context switches.

The importance of the problem, has already raised the attention of the researchers and study in this field still continues. Some more important works are listed below.

Albielmona [3] did an overall review over many scheduling algorithms. Proportional share scheduling algorithm proposed in [4] combines the small overhead of the RR method by protecting the short processes. The capability of re-adjusting the weights, enables the algorithm to have a more fair behaviour.

Nieh et al. [5] proposed a new scheduling algorithm known as Virtual Time Round-Robin (VTRR) with complexity of O(1) by combining fair queuing algorithms with the RR scheduling algorithm.

Zahedi et al. [6] optimized the RR algorithm by using the concept of fuzzy rules and introduced it as Fuzzy rule based Round-Robin CPU Scheduling (FRRCS). They showed that the proposed algorithm, reduces the average waiting time.

The constraint of static time quantum is resolved in [7] by dynamically re-adjusting the value of the parameter repeatedly . Singh et al. [8] proposed a new RR algorithm and showed that their method, reduces the problems of the simple RR and increases the system throughput.

Mostafa et al. [9] introduced a new algorithm based on integer programming method to calculate the appropriate vale of the time quantum. Mohanty et al. [10] also developed a new algorithm called Shortest Remaining Burst Round Robin (SRBRR) based on minimum remaining burst time and showed that this method is more effective than common RR. Behera et al. [11] developed a new algorithm called Dynamic Quantum with Re-adjusted Round Robin (DQRRR) and experimentally showed that this method is more efficient than the classic RR due to less number of context switches.

A new RR scheduling algorithm is proposed in [12] in which the time quantum is calculated intelligently and individually for every task. The researchers showed that the throughput of the system is increased due to the decreasing the total number of context switches.

Behera et al. [13] also proposed a method called Multi Dynamic Time Quantum Round Robin (MDTQRR) which dynamically calculated the vale of the time quantum and leads to an increase in system throughput.

Noon et al. [15] developed a new algorithm called AN, based on a new approach named dynamic time quantum which enables the operating system to adjust the time quantum according the burst time of the set of waiting processes in ready queue. Based on simulation ad experiment, they showed that their proposed algorithm solves the static(fixed) time quantum problems the and increases the performance of RR.

Alam [16] used fuzzy logic to determine the best quantum value in RR scheduling algorithm and claimed that the throughput of the system is not decreased due to unnecessarily context switches.

Suresh et al. [17] developed an algorithm to increase the quality of service in WiMax networks by proposing a Round Robin based scheduling mechanism which maintains the fairness among the users.

Raheja et al. [18] also developed an algorithm to determine the optimum time quantum value in Round Robin scheduling, based on vague and non-precise parameters using Linguistic variables and Mamdani Fuzzy logic and called it LRRTQ. The authors used Matlab software to implement the proposed algorithm and fuzzy interface system.

Nayak et al. [19] developed a new scheduling algorithm called Improved Round Robin (IRR) by dynamically calculating the time quantum value in order to decrease the average waiting time of the processes and total number of context switches.

Siregar [20] used Genetic Algorithm to determine optimum time quantum value in Round Robin CPU scheduling algorithm to minimize the average waiting time of the processes.

• III.    The Proposed Model

• 3.1    Assumptions

In this section, a non-linear mathematical model for optimizing the time quantum value in RR scheduling algorithm is proposed.

In the proposed model, it is assumed that:

• ■    There are n number of ready processes waiting in the ready queue to be dispatched circularly for the time being.

• ■    The burst time of each process in known and available.

• ■    The hardware system is uni-processor.

• ■    The context switching time is equal for all the processes.

• 3.2    Parameters

The parameters of the model can be listed as follows:

• ■    n : Total number of ready processes at the beginning time.

• ■    S i : Burst (service) time of the i th process.

• ■    TAT i : Turnaround time of the i th process.

• ■    W i : Waiting time of the i th process.

• ■    R i : Total number of the times which the i th process will seize the processor.

• ■    Lq i : The amount of the last time quantum which the i ^th process needs.

• ■    PP ij : Total burst time of the processes like j , that are waiting in the ready queue before the i ^th process, at the beginning time.

• ■    PS ij : Total burst time of the processes like j , that are waiting in the ready queue after the i ^th process, at the beginning time.

• ■    CT : Time needed for context switching.

• 3.3    Decision Variables

The proposed model includes only one decision variable:

• ■ q: The amount of time quantum.

• 3.4    The Mathematical Model

The model is proposed to minimize average waiting time of the processes as follows:

Min W =

И s.t.

TAT^(Rrl)(q-^T) + Ix3i + ^PPy + VPSy(2)

i<3

Wj-TATj-Si(

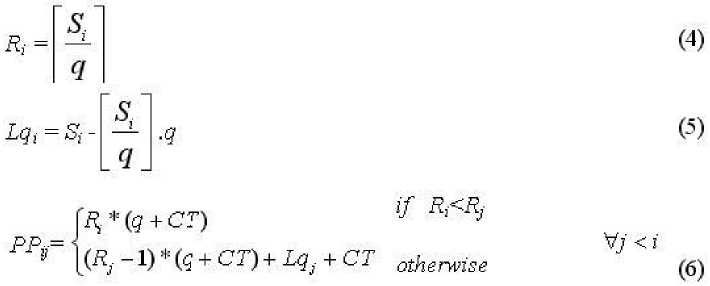
J(^-l)*(g + C7)         V R^Rj

• ⁸    V^-lVto + CT^ + Lq^CT   , .

• ³   ’ ^w ’   ⁴³ otherwise

q : integer>0;

where:

The main objective of the model, is the minimization of the average waiting time of the processes which is given in (1). The equation (2) calculates the turnaround time of the ith process which equals to number of the times that the process receives a complete quantum from the processor, including the context switching time, plus the amount of the last time quantum, plus total sum of execution times of the predecessor and successor processes of the ith process. The equation (3), calculates the waiting time of the ith process. Equations (4) and (5), calculate the total number of the times which the ith process will capture the processor, and the amount of the last needed time quantum respectively. The equations (6) and (7) calculate total execution time of the predecessor and successor processes respectively. The constraint of having an integer value for the decision variable q, is added in (8).

• IV.    Implementation and Computational Results

• 4.1    Example 1

The proposed model is implemented in Lingo 8.0 optimization software and solved over four selected problems from the literature. The problems' details and the computational results are discussed in the following subsections.

The first example is adopted from Mohanty et al. [10]. The details are listed in Table 1.

Table 1: Process specification of example 1

Process#

Arrival Time

Burst Time

1	0	13
2	0	35
3	0	46
4	0	63
5	0	97

The researchers in this paper, have proposed a method called SRBRR to calculate the value of the time quantum, and have compared the results with the classic RR algorithm with static time quantum equal to 25. The compared results in the original paper, along with the results obtained by the proposed algorithm, are listed in Table 2. The results show that the proposed model has obtained better values. The value of the context switching is assumed to be zero.

Table 2: Computational results of example 1 Used Method Time Quantum (q)         Average Turnaround Time         Average Waiting Time Static RR 25                               148.2                                97.4 SRBRR 17, 34, 46                           122.4                                71.6 Proposed Model 63                               113.2                                62.4 amount of context switching in the original paper is

• 4.2    Example 2

assumed to be zero.

The second example is adopted from Hiranval and

Roy [14] and the details are given in Table 3. The

Table 3: Process specification of example 2 Process#                 Arrival Time               Burst Time 1                                0                               14 2                           0                           34 3                             0                            45 4                           0                           62 5                             0                             77

The researchers of the reference, have proposed a new algorithm called Adaptive Round Robin (ARR) and have compared the obtained results with the classic RR method. This comparison along with the obtained values by the proposed method in this paper is given in Table 4. The results in this example show the superiority of the proposed model.

Table 4: Computational results of example 2

Used Method          Time Quantum (q)          Average Turnaround Time          Average Waiting Time

Classic RR                     25                              143.4                               97

ARR                      45                            117.4                             71

Proposed Model                   62                              108.2                                62

4.3 Example 3

processes are sorted decreasingly based on the burst time and context switching time is assumed to be zero.

The third example is also adopted from the research by Hiranval and Roy [14] as specified in Table 5. The

Table 5: Process specification of example 3 Process#                   Arrival Time                 Burst Time 1                                  0                                 83 2                             0                             54 3                               0                               30 4                               0                               19 5                                  0                                  8

The comparison of the obtained results in the original paper besides the results given by the proposed algorithm is shown in Table 6. As the values show, the proposed method has a better performance than previous methods over this example.

	Table 6: Computational results of example 3
Used Method	Time Quantum(q)          Average Turnaround Time         Average Waiting Time
Classic RR	26                                149.2                                110.4
ARR	45                               157                              118.2
Proposed Model	10                                 128                                 84.6

• 4.4    Example 4

The forth example is adopted from Noon [15] paper. As mentioned in section 2, the researchers in this paper have proposed a new method called AN to calculate the value of the time quantum in RR method of process scheduling and have compared it with dynamic RR algorithm. The problem specification and the computational results are given in Table 7 and Table 8.

Table 7: Process specification of example 4

Process#	Arrival Time	Burst Time
1	0	20
2	0	40
3	0	60
4	0	80

As the results show in Table 8, the proposed method has obtained the same values obtained by AN method, but better than that of dynamic RR.

Table 8: Computational results of example 4

Used Method	Time Quantum (q)	Average Turnaround Time	Average Waiting Time
AN Method	60	100	50
Dynamic RR	20	120	70
Proposed Model	60	100	50

• V.    Conclusions

In this paper, a new non-linear mathematical model is developed to calculate the optimum value of the time quantum in Round Robin process scheduling algorithm to minimize the average waiting time of the processes. The model is implemented in Lingo 8.0 software and four selected problems adopted from the literature are implemented and solved. In all the selected examples, the proposed method obtained utterly better or equal performance than the previous algorithms in the references.

Acknowledgement

The authors would like to thank Sama Technical and Vocational Training College, Tabriz Branch, Islamic Azad University for the financial support of this research, which is based on a research project contract.