Devanagri Handwritten Numeral Recognition using Feature Selection Approach

Published Online November 2014 in MECS

Recognition of offline handwriting is the process of automatic reading of handwritten information by computer system on a piece of paper. The process undergoes steps like Pre-processing, Segmentation, Dimensionality reduction and classification. The reason for the poor result of recognition is mainly due to variation in writing style, the dependency on the writing tool used by the writer, the variation in size and orientation of the written characters. Pre-processing is the process of data conditioning operation so that it qualifies the initial level for the succeeding steps. Dimensionality reduction is needed to improve the performance of the recognition results in terms of accuracy and speed. There are two methods of dimensionality reduction: Feature extraction and Feature Selection. In the real world classification domain the class probability and class conditional probability is often unknown a priori. Also often the feature suitable for particular classification test is not known in advance. Therefore feature selection [1] [2] [3] [4]become important in most of the classification algorithms. By reducing the number of features, one can both reduce over fitting of learning methods, and increase the computation speed of prediction. The feature selection is the process of selection, from the whole set of available features, the subset allowing the most discriminative power. The choice of a good feature subset is crucial in any classification problem. In Most of the classification algorithms we extract features out of which some of the features have more discriminating power for particular class than the others. These other features may be important recognition of some other class. So keeping this idea in mind a class wise feature selection algorithm is proposed. Feature selection for a feature set Y of cardinality N involves the exponential growth of the search space of the order 2N. Therefore, heuristic algorithms become necessary for finding near–optimal solutions. Feature selection methods can be classified into two types, filters and wrappers. The first type is classifier independent, as they are not dedicated to a specific type of classification method. On the contrary the wrappers rely on the performance of one type of classifier to evaluate the quality of a set of features.

The rest of the paper is organized as follows. Section II describes the major related attempt made for the recognition of Devanagri script. The proposed methodology is explained in section III, where the information about the feature generation, the criterion used for feature selection and the method of combination of classifiers is explained. Section IV presents the experimental results and section V describes the conclusion and future scope for improvement.

• II.    Related Work

  The research in Devanagri started in the year 1977 by Sethi and Chatterjee [5] . Authors proposed a decision tree based approach for constrained hand printed Devanagri characters using primitive features. Hanmandlu and Murthy [6] used fuzzy model based recognition for handwritten Hindi numerals, where they used Normalized distance as feature for individual boxes and obtained 92.67% accuracy. Sharma [7] used Directional chain codes features and calculated it for blocks in bounding boxes which are applied to MQDF based classifier for obtaining total likelihood of the character and obtained 98.86 % accuracy for numerals and 80.36 % for characters.. Bajaj et al [8] employed set of different features namely density, moment and descriptive component feature for classification of Devanagri numerals. They used multi-classifier connectionist

  architecture for increasing reliability and obtained 89.6% accuracy. Bhattacharaya et al [9] proposed a multilayer perceptron(MLP) neural network based classification approach for Devanagri numerals and obtained 91.28 % results. They used multiresolution features based on wavelet transforms. Rajan et al [10] proposed an efficient zone based feature extraction method for numeral recognition of four popular south Indian scripts. They used Zone centroid and image centroid based distance metric for feature extraction. Deshpande et al [11] proposed a regular expression based approach to Devanagri character recognition for increasing efficiency. In this approach the characters are first converted into sequences and then geometrical properties of characters are converted into regular expression which is used for matching purposes. Now the regular expression is tested with minimum edit distance. Chaudhari et. al [12] presented a pioneering effort for the development of handwritten numeral database of Indian scripts. For Devanagri characters Ensemble of classifier has been implemented by Satish Kumar et al [13] . In the paper author suggested a three tier approach wherein the first stage classify bar and not bar group of characters. After this separation, the further classification is done using different feature sets like Histogram, Profile, Edge based features etc. The overall recognition result obtained was 94.2 %. Agnihotri et al [14] implemented a system for Devanagri handwritten recognition using diagonal features and genetic algorithm for a dataset of 1000 samples and obtained 85.78 % match score.

• III.    Proposed Methodology

For the recognition of Devanagri characters the attempts made by various researchers cannot be compared because the dataset used by them were not common. The data in most of the previous efforts are generated by the research groups themselves. The benchmarking datasets were not there, but recently some dataset have been developed [12] for isolated numerals. So this study makes use of the above mentioned dataset. The method used by this study is materialized using steps of the block diagram shown in Fig. 1. The Input images from training and test dataset undergo the Preprocessing, Feature extraction, Feature ranking according to 'class to predict' criterion and classification using single as well as combination of classifier.

•

•

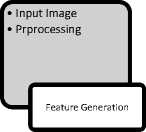
Normalization of features

Class wise feature Ranking and selection

Selection of set of z— Features for paricular classifier

•

•

Training of classifier using selected feature classification of unknown character

• X— Recognized character

• A.    Data Collection and Pre-processing

  The first benchmark for the offline Hindi Numeral was published in the year 2009 [12] . The Devanagri character benchmark dataset from CVPR unit is still not available for the research community. CVPR Unit of ISI Kolkata is the first unit affiliated to Internationally Recognized association IAPR (International Association for Pattern Recognition) and is providing one of the major efforts towards the recognition of Indian languages. The numeral dataset from CVPR unit consists of 22,556 images stored in ‘tif format collected from 1049 writers. From the dataset 200 images of each class are randomly selected and used for experimentation in our study. Some sample images from the dataset are shown in Fig. 2. The grayscale images are converted to two tone images. The bounding box of character image is obtained and then boundary is extracted. The details about Pre-processing and feature generation can be found in [15] . The output of pre-processing steps are shown in Fig. 3

Fig. 2. Image samples from ISI data set

After obtaining the boundary, features are generated for dimensionality reduction using histogram of gradient directions. The boundary image is divided into 9 compartments as shown in Fig. 4. Histogram is obtained as an accumulation done for each of these 9 compartments

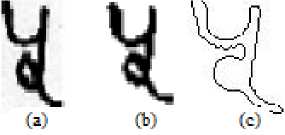
• B.    Feature Extraction using Gradient Direction

The gradient feature decomposition originally proposed for online character recognition by A. Kawamura et al [16] which reported a high recognition efficiency for Japanese characters. This method is applicable to machine printed/handwritten, binary/ grayscale as well as low resolution images. The calculated gradient of the image is decomposed into four, eight or sixteen directional planes. For our analysis we have taken eight directional plane. The Fig. 4 shows the gradient vector decomposition into their nearest vector plane. We have accumulated the magnitude of gradient in sampled eight directions for each of the subsection of original image.

Fig. 1. Proposed Approach

x(x, у) = f(x + 1, у - 1) + 2/(x + 1, у) + f(x + 1, у + 1) - f(x - 1, у - 1) - 2/(x - 1, у) + f(x - 1, у + 1) yy(z, у) = f(x - 1, у + 1) + 2/(x, у + 1) + f(x + 1, у + 1) - f(x - 1, у - 1) - 2/(x, у - 1) + f(x + 1, у - 1)

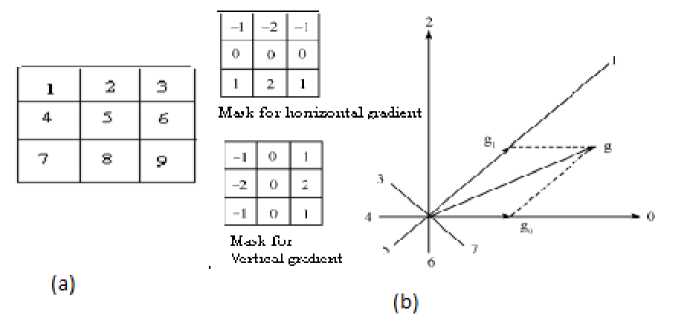
Fig. 4. (a) Zoning of bounding box of image(b) Gradient Feature Calculation Method

Conventionally the gradient is calculated on each pixel of the image. In our analysis we have applied ‘sobel’ edge detection algorithm to calculate gradient vector at each image pixel of preprocessed grayscale image. The gradient vector can be quantized into eight directions using angle vector quantization or vector decomposition using parallelogram rule. In the first method the magnitude of gradient in each image pixel is assigned to directional plane nearest to it and in the second method the gradient vector is decomposed into two nearest directional planes using parallelogram vector division rule. The parallelogram quantization method gives less quantization error so we have applied this method for quantizing directions of gradient vector.

• C.    Feature selection

The goal of feature selection is to search the most relevant features from a list of large number of features of a particular problem domain. Let X be the original set of features, with cardinality n . The continuous feature selection problem refers to the assignment of weights to each feature in such a way that the order corresponding to its theoretical relevance is preserved. Feature selection algorithms are characterized on the basis of the search organization, generation of successors and on the basis of evaluation function [17] . The classification of feature selection methods is given in Fig. 5 and more details about the methods and the criterion used for evaluation can be found in the survey paper by A. Belanche et al. [17] . For this study Filter method of feature selection is used whose evaluation criterion is based on mutual information. Some of the core definitions related to mutual information are explained in the following subsection.

• D.    Feature selection using Entropy and Mutual

Information

In feature selection problem, the relevant features have important information regarding the output, whereas the irrelevant features contain little information regarding the output. An experimental comparison of various feature selection algorithm applied to different classifiers is

reported by Bhalla et al [18] for the classification of Microarray data. The objective of feature selection is to find those features that contain as much information about the output as possible. For this purpose, Shannon’s information theory [19] provides a feasible way to measure the information of random variables with entropy and mutual information. MI is capable of measuring a general dependence between two features without assuming the distributions of the features, and case based reasoning requires no assumption on the different project features to derive the solutions.

Evaluation Measure

—Divergence

—Accuracy

-Consistency'

—Information

—Dependence

—Distance

Exponential Sequential Random

Generation of Successors

Forward Backward

Search , Organization

Fig. 5. Classification of feature selection algorithms [17]

The entropy H(X) is a measure of the uncertainty of a random variable X. For a discrete random variable X, with the probability density p(x), the entropy of X is defined as

H(X^ = -^p(x)/c>5p(x)

xeX

Here, the log base is 2 and entropy is expressed in bits. The joint entropy of X and Y with joint pdf p(x,y),

H(X,r) =

S xeX ^ уеУ p(x, y)logp(x, у)

When certain variables are known and others are not, the remaining uncertainty is measured by the conditional entropy,

H(YIX) = - i xeX p(x)H((YlX = x) = S xeX ^ ye Y P⁽x, y)Zoyp(x^|y)

Therefore, the joint entropy and conditional entropy has the following relation:

H(X,Y) = H(X) + H(Y|X) = H(Y) +H(X\Y)   (6)

The information found shared by two random variables is important in our work and it is defined as the mutual information between two variables:

I(X;Y) = -Z xeX

^ yeY

P⁽X, У)

logP (x|y) p⁽x)p(y )

Measurement level output of classifier 1

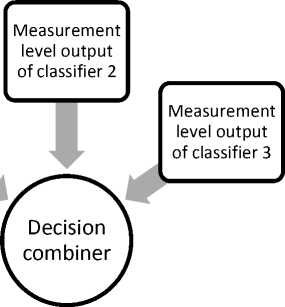
Fig. 6. Process of combination of classifier

If the mutual information is large, the two variables are closely related. If the mutual information becomes zero, the two variables are independent. The probability of the individual i being selected is given by:

S i = 1 iU KXv.Y^- E 7=1 1 (Xi; Xf) (8)

where X i is the input and Y is the output. The above mention criterion is known as Maximum relevance minimum redundancy based feature selection which was introduced by Peng et al [20] .

• E.    Artificial Neural Network based classifier (ANN-10, ANN-20, ANN-30)

A standard feed forward network with one hidden layer of 10 neurons and sigmoid transfer function is used as classifier. The network is trained by the back-propagation learning algorithm using the MATLAB Neural Network toolbox [21] . The 10 output values are normalized and used as posterior probabilities. Again experiments were conducted with 20 and 30 neurons in the hidden layer.

• F.    Classifier combination module

According to the level for a pattern recognition task, classifier combination can be grouped as: Feature level combination and the decision or score level combination out of which the score level combination is most popularly used. This is due to the fact that the knowledge of the internal structure of classifiers and their feature vectors is not needed in the score level. Though there is a possibility that representational information is lost during such combinations, this is usually compensated by the lower complexity of the combination method and superior training of the final system. After calculating the measurement level output using posterior probabilities {pij (x'), i = 1, m; j = 1, c } for a m classifiers and c classes, fixed combining rules are used as decision combiner [22]. The confidence qj (x) for class j is computed by qj (x) = Rulei ^Pij (x)) (9) q;(x)

q f ^(x)= i-^) ⁽¹⁰⁾

The following combiners are used for rule given in equation (9): Majority Voting, Maximum, Sum, Minimum, Average, Product.

Although the classifier ensemble had been used by many researchers, the novelty of our work is that we applied a MRMR Feature selection based classifier ensemble method for the recognition of Hindi Numerals.

IV. Experimental Results

Experiments are firstly performed on numeral images. Individual classifier recognition rate as well as using committee of classifier is obtained without feature selection. The results are shown in table 1. The time mentioned in the table include the time for training, the time for testing as well as the time for feature selection (when used). The time for pre-processing and feature extraction is not included in the results. Also the feature selection method uses the class dependent feature selection method for obtaining features for specific class. The feature vectors are combined to form the resultant feature vector. The Results are showing the effectiveness feature selection based ensemble over the single classifier. The Experiments are conducted on 2000 image samples from ISI dataset, out of which 70% used for training and 30% used for testing. The Proposed strategy produces the results comparable to [23] with only 200 sample image per class. This strategy will be effective for dataset of small size, as in Hindi only a limited dataset is available in public domain.

From the results presented in table - I, it is clear that the recognition rate is low if all 72 features are used with a average processing time of 1.9 sec for a single image. However when the feature selection criterion with selection on the basis of class to predict is used the recognition performance improves by 5%. The time needed for processing of a single image is 2 second.

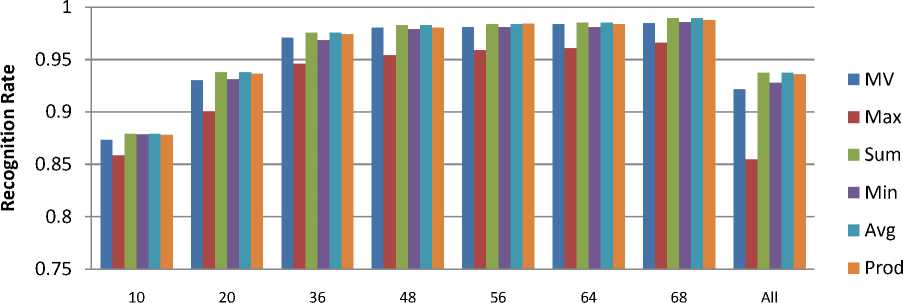
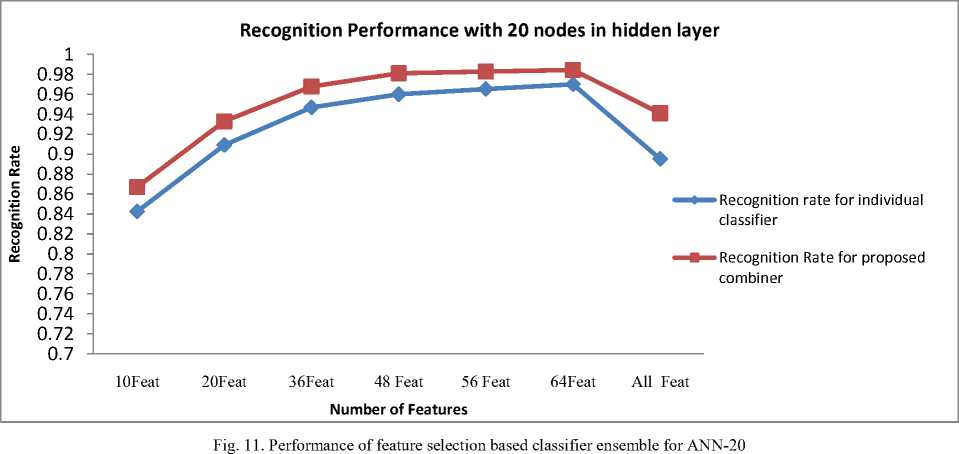
The result of combination of classifier as shown in Fig. 7-9. It is clear from the figures that the recognition performance of proposed method with 48, 56, 64 features is considerably good. Also recognition performance of the proposed method with 48 features gives 98% and above recognition efficiency with processing time reduced to half of the time required for features greater than or equal to 64 with ANN-30.

Table 1. Recognition Performance by varying number of features

Number of Feature	Recognition Rate for Single classifier	Recognition Rate of combiner	Time for the Recognition (sec)	Recognition Rate for single classifier	Recognition Rate of combiner	Time for the Recognition (sec)	Recognition Rate for single classifier	Recognition Rate of combiner	Time for the Recognition (sec)
	Using 10 nodes in hidden layer			Using 20 nodes in hidden layer			Using 30 nodes in hidden layer
10Feat	0.80805	0.8355	332	0.8424	0.867	490	0.8612	0.879	711
20Feat	0.89433	0.9207	348	0.9091	0.9328	686	0.9135	0.938	1346
36Feat	0.9459	0.9655	431	0.9467	0.9677	852	0.954	0.9758	2032
48 Feat	0.9615	0.9793	569	0.9599	0.981	1182	0.9636	0.9827	2250
56 Feat	0.9644	0.9832	645	0.9652	0.9827	1257	0.968	0.9843	2470
64Feat	0.9622	0.9808	904	0.9699	0.9843	1735	0.9692	0.9853	4078
All Feat	0.8796	0.9322	574	0.8952	0.941	1449	0.8833	0.9375	3812

The Recognition results for 10 nodes in hidden layer

1.2

ш го се

0.8

о

0.6

ш о ш се

0.4

0.2

IIIIIIIII III

• ■    MV

• ■    Max

• ■    Sum

• ■    Min

• ■    Avg.

• ■    Prod.

10 Feat

20 Feat

36 Feat

48 Feat

56 Feat

64 Feat

All Feat

Number of Features

Fig. 7. Performance comparison of proposed approach with the single classifier with 10 nodes in hidden layer.

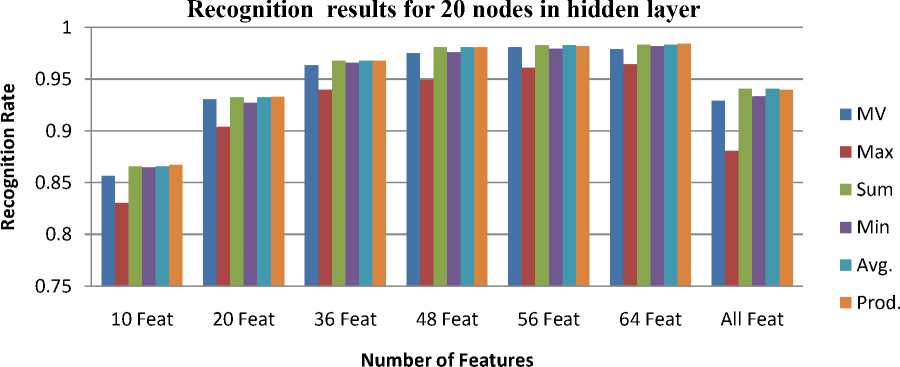
Fig. 8. Performance comparison of proposed approach with the single classifier with 20 nodes in hidden layer.

Recognition Result for 30 nodes in hidden layer

Number of Features

Fig. 9. Performance comparison of proposed approach with the single classifier with 30 nodes in hidden layer.

&

is

ы

1 0.98 0.96 0.94 0.92 0.9 0.88 0.86 0.84 0.82

0.8 0.78 0.76 0.74 0.72

0.7

Performace of Proposed combiner with 10 nodes in hidden layer

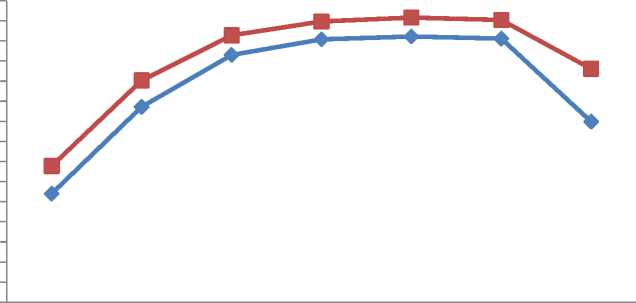
10Feat      20Feat      36Feat     48 Feat     56 Feat      64Feat     All Feat

Number of features

^^— Recognition rate of individual classifier

■ Proposed combiner

Fig. 10. Performance comparison for feature selection based ensemble for ANN-10

1 0.995 0.99 0.985 0.98 0.975 0.97 0.965 0.96 0.955 0.95 0.945 0.94 0.935 0.93 0.925 0.92 0.915 0.91 0.905 0.9 0.895 0.89 0.885 0.88 0.875 0.87 0.865 0.86 0.855 0.85

Recognition Performance with 30 nodes in hidden layer

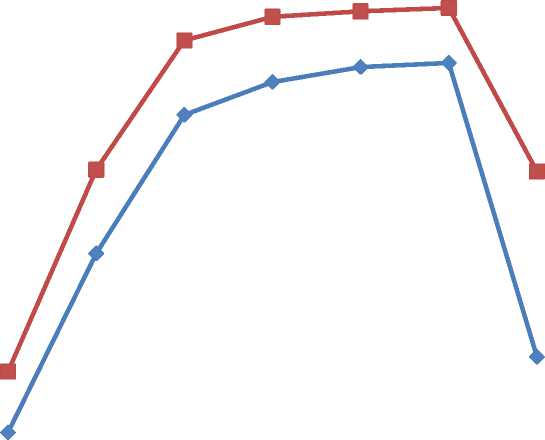
■ Recognition Rate for proposed combiner

10Feat      20Feat      36Feat     48 Feat     56 Feat     64Feat     All Feat

Recognition rate for individual classifier

Number of Features

Fig. 12. Performance of feature selection based classifier ensemble for ANN-30

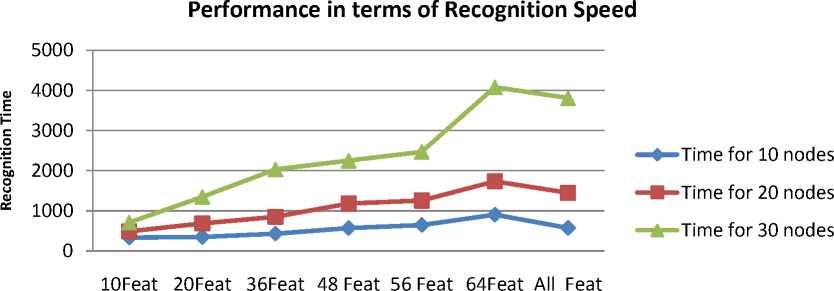
Number of Features

Fig. 13. Processing time for various patterns excluding preprocessing

• V. Conclusion

The contribution of the paper is to propose a feature selection based classifier combination algorithm for the handwritten Devanagri numeral recognition. The obtained results are verifying that (1) the combination of classifier is improving the recognition result by 2-3 % than the single classifier. (2) Selected feature based on proposed “class specific feature selection using MRMR” based optimization criterion gives better recognition result. The combination rules used belongs to low complexity combining algorithm results in faster recognition results. The experiments are ongoing and the method using complex combination rules are underway. In future the better recognition performance can be approached by increasing the complexity in combination algorithms.