Developing a Virtual Group Decision Support System Based on Fuzzy Hybrid MCDM Approach

Published Online January 2013 in MECS

The design and implementation of decision support systems that can introduce automation and intelligence to on-line negotiations is currently the focus of intensive research efforts. Negotiation models, however, are characterized as of relatively high complexity, since they involve evaluation and decision making in a state of uncertainty, based on multiple attributes (criteria) of quantitative and qualitative natures, involving temporal resource constraints, risk and commitment issues, varying tactics and strategies, domain specific knowledge and information asymmetries, etc [1]. On the other hand, the organizational decisions are often related to different, enormous and conflicting criteria and evaluations. For these reasons today’s fast changing global environments dictate that a successful enterprise has a rich decision-making process [2].

To encounter these situations, organizations implement decision support systems (DSS) in order to change data to information, comparison of the options and outcomes, saving of cost and time, effective teamwork etc. In addition, DSS enables organizations to manage virtual group decision making in which the disadvantages of face-to-face or conventional group involvement are removed. The common group processes losses cited in the literature includes dominance of one group member, production blocking, social loafing, free-riding, cognitive inertia, and information overload [3]. In contrast, DSS advantages are improving personal efficiency, expenditure problem solving, facilitates impersonal communications; promotes comprehension and training, and increased organizational control [4]. In addition the study [5] found that greater decision acceptance and willingness to work together obtained in virtual group decision making as compared to face-to-face group decisionmaking. Other advantages are storing data, transforming data to knowledge and information, and decreasing the possibility of conspiracy.

Different approaches introduced in the literature encounter multi-criteria decision making such as Analytical Hierarchical Processes (AHP), Elimination, and Choice Expressing Reality (ELECTRE) etc. However, since [6] proposed the decision-making methods in fuzzy environments, show an increasing number of fuzzy models introduced [7]. This approach is widely used because fuzziness and vagueness are usually present in the decision-making process.

The hybrid model of this paper uses modified fuzzy AHP and fuzzy Technique for Order Preference by Similarity to Ideal Solutions (TOPSIS) in the form of decision support systems. FAHP utilizes linguistic variables expressed in triangular fuzzy numbers to assess weights of criteria. However, to avoid quickly increasing pair-wise comparison when alternatives are immoderate, fuzzy TOPSIS is used (instead of FAHP) to find each alternative’s closeness coefficient. In addition, this hybrid model takes in different backgrounds such as experience, education, organizational rank and work history of decision makers in to consideration. The contribution of this paper is constructing a decision support tool which can manage the complicated process of decision-making in an organization effectively and easily.

This paper is organized as follows. Section 2 reviews the basic concepts and formulation of fuzzy approach. Section 3 presents the proposed method. The architecture of DDS is explained in section 4. Finally, section 5 concludes this paper with the remark of a decision support system named as Fuzzy Group Decision Making (FGDM).

• II.    Methodology

  • 2.1    Definitions

    • 2.1.1    Fuzzy Number:

Fuzzy concept was introduced by [8] to overcome the vagueness of information. A positive triangular fuzzy number (TFN) defined as A =(l,m,u) shown in Figure 1 and the membership function defined as (1).

	' ( x - 1 )                  ' ------ if l <  x <  m ( m -1 )
B a ( x ) = *	( u - x ) ------- if m <  x <  u >  (u - m )

0       Otherwise

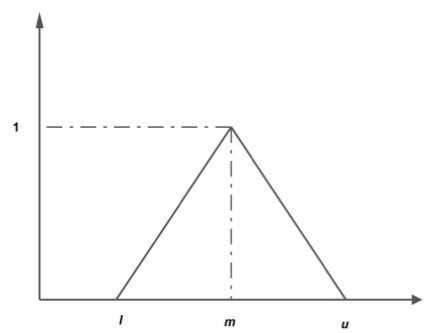
Fig 1: Triangular Fuzzy Number (TFN)

A 0B = (lx /u^, mx / m2,ux /l2)

~ - 1

A   = (1/ux ,1/mx ,1/lx)

• 2.1.3    Fuzzy Distance:

• 2.1.4    Linguistic Variables:

• 2.1.2    Operation on Fuzzy Numbers:

The distance between two fuzzy numbers A=(l i ,mi,ui) and B =(l₂,m₂,u₂) is calculated by 3-dimentional Euclidean distance:

a ( A , B ) = . -[( l , - l ₂)² + ( m_x -m₂ )² + ( u - u ₂)²

2                                          (8)

Linguistic variables are variables whose values are words or sentences in a natural or artificial language [9]. In this paper, decision makers use linguistic variables shown in table 1, to evaluate the importance of criteria, and Table 2 for rating the alternatives with respect to each criterion.

Let A and B be two TFN given by A =(l₁,m₁,u₁) and B =(l₂,m₂,u₂) respectively and p is a real positive number. Some algebraic operations of TFN are as follows:

for l, m, u >0 :

A Ф B = ( lx + 1 2, mx + m 2, ux + u 2) (2)

~~ A ® B = ( 1 1 l 2, m 1 m 2, u 1 u 2)

AQB = ( lx - u 2, mx - m 2, ux - 1 2)

~ p ® B = ( p l 1 , pm 1 , p u 1 )                     (5)

Table 1: Membership functions of the seven levels of linguistic variables for rating alternatives

Fuzzy Number	Linguistic Scales	TFN	TFN Reciprocal
9	Absolutely important	(7,9,9)	(1/9,1/9.1/7)
7	Very      strongly important	(5,7,9)	(1/9,1/7,1/5)
5	Essentially important	(3,5,7)	(1/7,1/5.1/3)
3	Weakly important	(1,3,5)	(1/5,1/3,1)
1	Equally important	(1,1,3)	(1/3,1,1)
2,4,6,8	Intermediate values

Table 2: Membership functions of the seven levels of linguistic variables for rating alternatives

Fuzzy Number	Linguistic Scales	TFN
10	Very Good	(9,10,10)
9	Good	(8,9,10)
7	Relatively Good	(6,7,8)
5	Moderate	(4,5,6)
3	Relatively Week	(2,3,4)
1	Week	(0,1,2)
0	Very Week	(0,0,1)
2,4,6,8	Intermediate value between judgments	two adjacent

• 2.2    Fuzzy Analytic Hierarchical Process:

AHP introduced by [10] allows for the application of data, experience, insight, and intuition in a logical and thorough way. However, the AHP method does not take into account the uncertainty associated with the mapping while the AHP’s subjective assessment, selection and preference of decision-makers have great influence in the success of the method [11]. Decisionmakers usually find that it is more accurate to give interval assessments rather than fixed value merit. [12] Therefore, based on a fuzzy paradigm introduced by [8], fuzzy AHP is used in which local and global priorities from fuzzy preference ratios are derived. We derive fuzzy weight of pair-wise matrix elements by calculating the matrix eigenvalues according to (9) [13].

n      mn

• s ,    = Ё M .i ^x i ZZ M jV

j = 1             i = i ^j = 1                                   (9)

where M is triangular fuzzy number and k, i and j represent matrix row, alternatives and criteria respectively.

• III.    Proposed Method

• 3.1    Data Input

A decision support system named as Fuzzy Group Decision Making (FGDM) is programmed to utilize fuzzy AHP and TOPSIS. Figure 2 indicates the flow diagram of the system. Let’s suppose a virtual decisionmaking committee with k members who intend to rank i alternatives with respect to j criteria. The administrator is responsible for selection of best alternative .

• 1)    FGDM includes three databases:   Criteria,

Alternatives and Decision makers. The manager logs on to the system, sets a new project name, chooses decision-makers and sets username and password for each one. Now each member can access to the system to assess the importance of criteria and rate each criterion with respect to the alternatives.

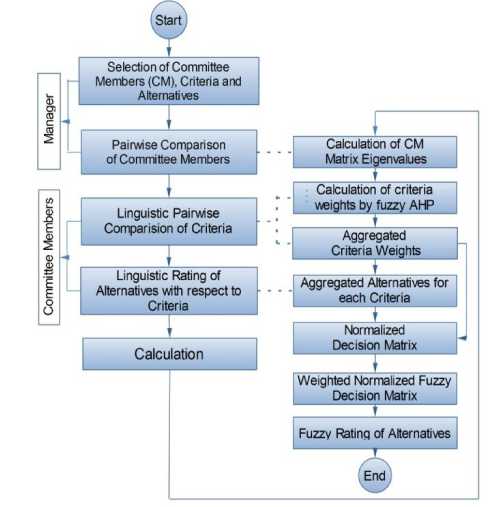
Fig. 2: The steps of problem formulation and calculation

• 2)    The decision-makers naturally have different backgrounds such as educational achievement, job history and organizational status. Therefore, it is expected that these factors may affect their final assessments.  Take  in these factors in to

consideration, the  manager  uses pair-wise comparisons between his team members based on correspondence circulated to different departments and it is establishing a base for appraisal evaluation objectives as well. Some methods have been introduced to weight decision-makers. For instance, [14] suggested the use of interpersonal comparison to obtain the values of scaling constants in the weighted additive social choice function. This weighting will be used in further calculations.

• 3)    Based on these comparisons, the weighting factors of members according to (10) are calculated and stored in memory [10]:

  DM ^k . e

  
  

  w = lim

  ,^ e^TDM^k e

  
  
  
  

in which e^T = (1,1,1,…,1) and DM is comparison matrix of decision-makers. When the difference between DM^k and DM^k+1 can be neglected the computation is stopped and the data stored in a weighting vector:

D = ( D i , D 2 ,..., D , )

• 4)    Choosing the adequate criteria is the next step which is based on a decision disposition. There are no limitations in criteria and alternatives selection. However, increasing the number of selections raises the inconsistency of pair-wise comparison in further steps.

• 5)    Another step is alternative (for instance, supplier) selection. Figure 3 indicates the selection window of criteria, alternatives and decision makers.

• 6)    Now each member log on to FGDM and assess the importance of the criteria and rate alternatives with respect to criterion in two adjacent questionnaires. There is a pull-down menu in the first questionnaire to facilitate the comparison and a seven-point scale (checklist) in the second one to rate the alternatives linguistically. Less uncertainty becomes the advantage of paired-comparison for individuals; it is more of a convenience than an absolute comparison [15]. Table 3 indicates the assessment of the importance of criteria by two typical users. It is seen that these two people have different ideas for the importance of criteria. While the first believes that the importance of C₁ against C 4 is low, the other sees it as “absolutely high”. These decision makers come from different organizational departments. When two or more organizational departments  strive for mutually

• 3.2    Calculation

acceptable purchase choices or attempts to agree on an issue such as product specification and vendor capabilities, a potential conflict becomes present [16].

• 1)    When the members fulfilled their assessments, the manager logs on to the system in order to calculate the results.

• 2)    The linguistic variables are transformed to their equivalent fuzzy numbers by the scale indicated in Table 1 and 2 and weighted variables are calculated using (11). Suppose p=1,...,k decision makers believe the importance of j=1,...,n criteria as those indicated in Table 4 in which w jk is a triangular fuzzy number [17].

• 3)    In order to aggregate fuzzy weights of each criterion, we use the following method:

  ~

  w jk = ( w 1 , w 2 , w 3 )

  
  
  
  

~

wj = (wj 1, wj 2, wj 3)

in which

wj 1 = mnw jk 1},

k

1 ^k

• *>2 =TL wk 2

^k j = 1

w 3 = max w jk 3^}

k(14)

• 4)    The second questionnaire is the rating of alternatives with respect to each criterion indicated in Table 5 in which      is a fuzzy triangular

number:

~

r jip   (anmk , bnmk , c nmk )

The aggregate fuzzy rating of alternatives on various criteria can be calculated as follows:

~ r ji    (anm , bnm , c nm )

in which a nm

b nm

cnm

= min!anmk } ,

i

K

= T-Уь , k      nmk , k =1

= maxlc nmk } k

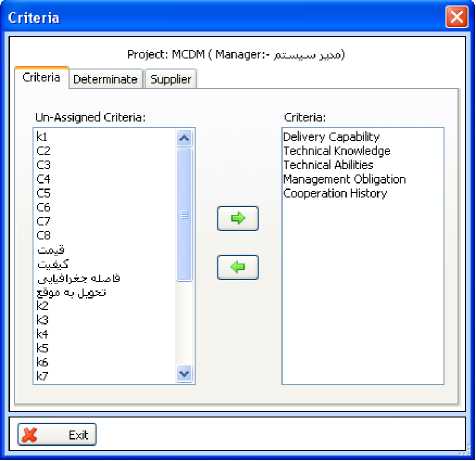
Fig. 3: Selection of criteria, alternatives and decision makers

Table 3: The importance of criteria assessed by two people

D 1	C 1	C 2                C 3	C 4	C 5
C 1	Equal	Equal            Low	Low	Low
D 5	C 1	C 2                C 3	C 4	C 5
C 1	Equal	Relatively High         High	Absolutely High	Absolutely High
Table 4: The weight of n criteria
C n / D p		D 1                  D 2	………	D k
C 1		w 11                     w 12		w 1k
C n		w j1                        w j1	………	w jk

Table 5: Rating of m alternatives by k decision makers

Criteria	Supplier	Decision Makers
		D 1	D 2             ……	D k
	S 1	r 111	r 112	r 11k
	S 2	r 121	r 122	r 12k
C 1
	S m	r 1m1	r 1m2	r 1mk
	S 1	r n11	r n12	r n1k
	S 2	r n21	r n22	r n2k
C n
	S…m	r nm1	r nm2	r nmk

Table 6: Fuzzy Decision Matrix

Alternatives	Criteria
	C 1	C 2              …….	C n
S 1	r 11	r 12	r 1 n
S m	rm 1	rm 2            ………	r mn

The new decision matrix illustrated in Table 6.

5) The scale of criteria could be different and to avoid complexity in calculations, the linear scale transformation is used to transform different criteria scales in to comparable scales. The normalized decision matrix can be expressed as

in which

c*= maxc# , j e B

i and

~ rij

R = [ ry ]

ij m x x n

( a? ,ai_ ^O^l. ) ^cij ^{, b}ij ^{, a}ij

The criteria itself could be benefits or costs. We denote the set of benefit criteria as B and the set of cost criteria as C . Then

in which a - = max a.. , j e C i                        ij

~  abc

r.. = ( _jj*L )ij V * ,    * ,    * X cj cj cj

• 6)    Now the product of normalized decision matrix and aggregate fuzzy weights of each criterion is obtained in order to calculate the weighted normalized fuzzy decision matrix Ṽ

~

V = [v ] ,                              z

L ij m x n , i =i,..,m  , j =i,_,n            (21)

CC = —--- , i = 1,...,m i  d * + d -

~~ v ij = Г„ . w j where         ij j

7) There are two solutions: positive and negative ideal solution results. If we consider the objective space of the two criteria C1 and C2 as indicated in Figure 4, A+ is the positive ideal solution, A— is the negative ideal solution, S1 and S2 different alternatives, d1* and d1- the distance between S1 to positive and negative ideal solution, d2* and d2- the distance between S2 to positive and negative ideal solutions. As in Figure 4 the relative distance between positive ideal solution A* and S1 are shorter than S2, therefore, the ranking of S1 is preferred as  opposed to S2 [18]. The fuzzy positive-ideal solution (A*) and fuzzy negativeideal solution (A-) can be defined as (23).

This coefficient represents the distances of alternatives to the ideal points simultaneously. It is seen that if the alternative reaches A^* or S_i=A^* then d_i^*=0 and CC_i=1 and if the alternative reaches A^- or S_i=A- then d_i^-=0 and CC_i=0 . It means when the alternative goes toward A^* or farther from A^- then CC_i goes toward “1”. In addition, if the alternative goes toward A^- or farther from A^* then CC i goes toward “0”.

3.3 Output Results

It is more realistic if the assessment overview of alternatives is described by linguistic variables in accordance to their closeness coefficient. Therefore, the interval [0, 1] could be divided into sub-divisions. Five sub-divisions are popular as indicated in Table 7 [19].

~~   ~      ~~   ~

A = ^{( v} ,, ^v 2 ,..., ^v_n), A = ^{( v} i ,^v ₂ ,..., ^v „ )

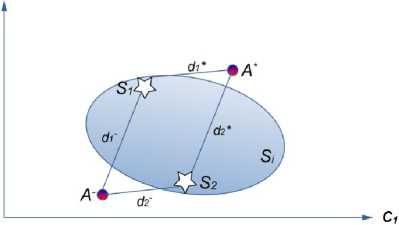
Fig. 4: The distance between positive and negative ideal solution for two alternatives

Table 7: Approval status of ranked alternatives

Closeness Coefficient		Assessment Status
CCi E	[0.0,0.2)	Do not recommend
CCi E	[0.2,0.4)	Recommend with high risk
CCi ^	[0.4,0.6)	Recommend with low risk
CCi ^	[0.6,0.8)	Approved
CCi G	[0.8,1.0]	Approved and preferred

where

»                         -

~~

Vj = max{Vj2} , Vj = min{Vj 1}

and the distance of each alternative from these two ideal points ( A^* and A^- ) can be calculated by Euclid's formula (refer to (25) and (26))

n di =A z (Vij -vj)2 v j =1

d f =

n

z (Vj- - V J )2

j = 1

8) The relative closeness of alternatives is defined by a closeness coefficient in order to determine the ranking order of alternatives:

IV. The Architecture of Proposed DDS

FGDM was programmed by C# (pronounced see sharp) language. This is a multi-paradigm programming language encompassing imperative, declarative, functional, generic, object-oriented (class-based), and component-oriented programming disciplines and was developed by Microsoft within the Dot NET initiative. FGDM enables decision makers to log to the system from their offices, compare the importance of criteria and rate the alternatives with respect to criterion. This comes from a Microsoft SQL server which is a relational model database produced by Microsoft Co. The available options depend on the user. If the user is an administrator all features are active. When the other team members log on, there are two adjacent questionnaires, for pair-wise comparison of criteria and for rating the alternatives with respect to each criterion both linguistical. To configure the program it is necessary to attach the FGDM database to the Microsoft SQL server. A common personal computer with 1 GB of RAM, 5 GB of disk space and connected to the local network is the minimum hardware requirements for running FGDM on client and server sides.

• V. Conclusion

Acknowledgment

The authors would like to acknowledge Sapa ElectroOptics and Laser Company, Isfahan, Iran for their comprehensive support and funding of this work. We would also like to thank Rayan Afzar-e-Novin Company, Isfahan, Iran for programming the (FGDM) software based on the proposed model.