Development a New Crossover Scheme for Traveling Salesman Problem by aid of Genetic Algorithm

Published Online December 2019 in MECS

The evolution of genetic algorithm (GA) was inspired by closely examining and replicating biological evolutions such as reproduction, recombination and mutation. Over the years, GA has become one of the most important methods for obtaining approximate solutions of optimization problems. GA works by letting the competing variables interact with one another to evolve a potential solution naturally. A significant number of practical optimization problems of various types spanning diverse areas of engineering, computing and natural sciences have been solved by the application of genetic algorithm.

The basic principles of Genetic algorithms (GAs) were introduced by John Henry Holland [1]. The aim of a GA is to achieve better results through selection, crossover and mutation. The success of any GA procedure depends on the working mechninasim of its search operators along with their appropriate integration.

Traveling salesman problem is one of the most famous benchmark, significant, historic and a hard combinatorial optimization problems [2]. In this problem, a salesman visits all the respective cities (nodes) and return back to the starting destination in order to complete a tour. Each and every city should be visited exactly once is the constraint. It has many applications such as the variety of vehicle routing [3], scheduling [4] and bioinformatics can easily be transformed into the TSP. On the basis of the distance evaluation plan, we divide the TSP into two different groups, called, symmetric and asymmetric. It is symmetric when c ij = C ji , V i, j, where i and j represent the row and column of a distance matrix respectively, otherwise asymmetric i.e. c ij ^C ji . The given ‘ n ’ cities, a distance matrix C = [ cij ] _n×n is searched for a permutation λ.

X : { 0,_.,n-1 }^- { 0,....,n-1 }, where c ij is the distance from city i to city j , which minimizes the traveled distance, f (λ, C).

f (A,C) = Z^ d( С_хщ, C _X(i+ц + C_X№, C _X( d) (1)

where λ(i) indicates the location of city i in each tour, d(c_i, c j ) is the distance between city i to city j and ( x_i, xj ) is a specified position of each city in a tour in the plane, and the Euclidean distances of the distance matrix C from a city i to another city j is expressed as:

Сц = ТСуТ- У/Р + С^Тл^Р ; i , j = 1,2,, п - 1 (2)

This problem is easy to understand but very difficult to solve i.e. for ‘ n ’ cities, there are n! possible ways to find the tour for asymmetric and у for symmetric TSP. There are approximate 10155 different tracks for only 100 cities. This is the reason to call it as a non-dererministic polynomial (NP-hard) problem [5]. The NP-hard problems cannot be solved using traditional optimization approaches like gradient-based algorithms. To achieve the optimum or near to optimum solution within a limiting time, heuristic approaches are efficient at handling the NP-hard problems [6,7].

The rest of this article is presented as follows. In Section II, we briefly review the related works. Crossover operators for TSP are described in Section III. Theoretical background of the proposed operator is presented in Section IV. Section V introduces the performance evaluation with testing methodology. Finally, Section VI provides a conclusion about the study.

• II.    Related Works

TSP is very carefully studied problem and received considerable attention over the last five decades. Several algorithms have been presented to handle this problem by researchers. These algorithms are generally divided into two groups; exact and approximate algorithms. The branch- and-bound [8] and cutting planes [9] are the two examples of exact algorithms which are excessively time consuming especially in large scale problems. Approximate algorithms are further classified into heuristic and meta-heuristic algorithms. There are three classes of the heuristic algorithm; tour construction, tour improvement and composite methods. To add an unvisited city to the solution at each step and try to shorten the initial solution are tour construction and tour improvement methods respectively. Finally, the composite method is the combination of these two algorithms.

During the last three decades with the appearance of meta-heuristic algorithms, a new era of study about optimization problems and their applications has been started. These search algorithms have also been applied on TSP such as: particle swarm optimization [10], simulated annealing [11], ant colony optimization [12], neural network [13], tabu search [14], and genetic algorithms [15-17]. We also used GA in this research to solve the TSP.

In literature, there is a lot of variety of the GA operators i.e. selection, crossover and mutation. Among these operators the crossover has a significant importance for TSP. A survey study about GAs approaches for TSP was presented with three new variations for order crossover were presented with improvements in [18]. A profit-based genetic algorithm with TSP and obtaining good results to test on networks of cities of Poland was presented [19]. A comparative study of various crossovers with the modified form of cycle crossover operator for TSP was presented [17].

• III.    Crossover Operators (Path-Based) for Tsp

The TSP is a combinatorial problem so the classical crossover operators such as one-point, two-point and uniform crossovers cannot be directly applied to pathbased GAs. To address the issue of the legality of an order, various crossover operators for path-based GAs have been proposed. Since these offspring share the characteristics of their parents, hence there must be a rule to make a combination of these characteristics. To generate offspring from a combination of the pair of paths, any random point is selected in such a way that it takes the first portion from one parent and the second portion from the other parent. This approach is called a 1-point crossover. As a result, there may emerge some infeasible solutions which can be avoided by putting a constraint that only feasible solutions can enter into coming generation [20]. Whereas in 2-point crossover (2PX), the expansion proceeds with a random selection of two points. Since the middle portion is exchanged here [21], hence it may also become infeasible. To overcome this problem, [22] randomly insert missing bits in the middle portion. Another approach to counter this problem is a Partially-mapped crossover (PMX), where the indexes are exchanged within the cut-points portion and missing bits are replaced with their mapping index in the other parent [23]. The order crossover (OX) is the next more commonly used operator of 2PX, in which the central part (from point a to point b, where a < b) is taken from one parent and another parent is selected from b + 1 point circularly onward to complete the legal offspring [24].

The cycle crossover (CX) is the next crossover operation, which is unusual, in its nature, and detects a set of cycles between two mated candidates in their bits and later it duplicates these generated cycles one by one to offspring [25]. To generate more offspring, a multioffspring genetic algorithm (MO-GA) was proposed by Wang et al. [26]. It builds offspring preserving the relative sequence of bits of one parent by choosing a subtour of another parent. First of all the parent’s track is divided into three regions after applying two random cut points. This scheme produces four offspring in two stages. In the first stage, its work similar as OX. In the second stage, exchange regions 1 and 2 or simply de-track the original tracks of parents. Find region 3 elements from the first new parent, delete the corresponding ones in the second new parent, and vice versa. After this the regions 3 of both parents are replaced with each other for producing offspring. We also proposed a new multioffspring c rossover operator in this study which presented in Section IV.

• IV.    Theoretical Background of Proposed Crossover Scheme

• A.    Biological theory foundation

In the literature, the GA for TSP explains a pair of parents producing a pair of offspring [27]. However, the biological evolution proceeds in such a way that it generates equal to or less than a pair of parents, which is uncommon. Since having the risk of extinction the generation or being less competitive, it is desirable to have the number of offspring more than two in genetic. When the number of offspring is larger than 2 from two better parents, there is more competition among them to survive, with increases chances of better offspring.

• B.    Mathematical ecological theory foundation

The probability of extinction of species can be illustrated by supposing that a pair of species has only two offspring at first. The probability of population size leads to “0” at a certain time “t” can be defined as:

• ( ...       ) = Л "exp ((„--y-)t) -у-

• 0                 у + exp (bi--у )t)-у'

where n and n + are the mortality and fertility rates respectively. This population can be extinct with time elapsing by the following probability:

Po(t) = [p0(t | i = i)] = [^^L--ZkM

• 0         L uv  i          j|i- exp((t)--у -)t)—у-J

As t→∞, there are three scenarios of (4) can be observed:

• (1)    When the mortality rate equals the fertility rate i.e. П - = n + , (4) is expressed as a series of exponential terms. Letting n + — n - = r , then P 0 (t) as t^ ™ should be

p_B (н^мЧ ?<Ч (5)

|ч-(1 +rt+—)-4-J

If n - equals to n + , then r^0, so we are eliminating r and higher terms and get the following expression:

Po (0 ^         ]' ^ pqq'    (6)

(у - +?y-rt)-у         L(r+?y-rt)J

Using n- = П+, we have lim P-^]1 = 1            (7)

^ot> 1+?7-tJ which means that the species should become extinct with 100% probability, even when the mortality rate equals to the fertility rate.

• (2)    If the mortality rate is higher than fertility rate in each generation, i.e. n - > П + . Letting n^+_ n - = ^{_ r} , then the exponential terms of (4) would be “0” when t→∞ and we get

₽ o (H i - exp:-:;-я '            (8)

Finally, it leads to lim(Pu(t)) = 1 t ^ oo

Hence, in this scenario with growing the time, species should become extinct.

• (3)    If the mortality rate is less than fertility rate in each generation, i.e. n - < n + , the (4) as t^™ can be expressed as follows:

Po (t) ^ p^^C] '

• 0         Lt, -exp (t) - у J

Hence, l im№,(t)) = Ы' t ^o

According to Eq. (9), there is no guarantee that such a population will never become extinct because a finite probability exists for the extinction. However, if the mortality rate is much lower than the fertility rate, then we have the least probability of biological extinction survive a long time when fertility rate is higher than mortality rate.

C. Proposed crossover scheme (Path-based)

In this section, we propose a new crossover scheme which is producing four offspring, two from each technique of PMX as well as the new one being proposed in this article. The current research intends to part ways from the conventional method of PMX technique, by introducing a newer approach which is mapping the existing bits from outside the cut-points, so we suggested it as a modified form of PMX. The newer scheme, by combining both PMX and its modified form can be termed as a multi-offspring partially-mapped crossover (MO-PMX). Hence, we differentiate MO-PMX in the following steps:

Step 1: Randomly select two individuals as parents for the mating process.

Step 2: Apply two random cut points on these parents.

Step 3: The portion between the cut points is exchanged into offspring.

Step 4: All those bits of the first parent, which are not present in offspring 1 and 3, placed at same locations (see Fig. 1 . ). (Note: Offspring 1 and 3 come from first parent by using techniques PMX and its modified form respectively.

Step 5: All those bits of the second parent, which are not present in offspring 2 and 4, placed at same locations (see Fig. 1.). (Note: Offspring 2 and 4 come from second parent by using techniques PMX and its modified form respectively.

Step 6: Now for left bits in offspring 1 and 2 (from PMX) are mapping within the cut-point portion of the parents.

Step 7: Also for left bits in offspring 3 and 4 (from a modified form of PMX) are mapping outside the cutpoint portion of the parents.

The complete scenario of this proposed approach is depicted in Fig. 1.

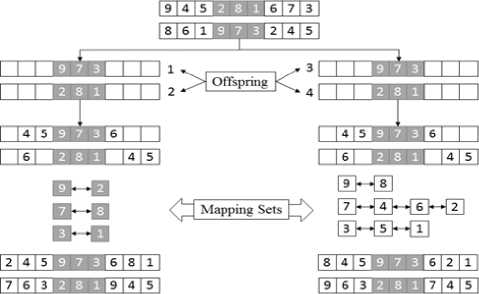
Fig.1. The proposed MO-PMX operator

To apply this crossover operator, we devised a MATLAB code for GAs and have given pseudo- code in Algorithm 1 .

Algorithm 1: The Pseudo-code of MO-PMX:

N ← no. of cities

P1← select random parent by selection method

P2← select random parent by selection method

Cut1← select a random cut of both parents

Cut2←select another random cut of both parents

Child1 ← P2 (cut1 to cut2)

Child2 ← P1 (cut1 to cut2)

Child3 ← P2 (cut1 to cut2)

Child4 ← P1 (cut1 to cut2)

% For Child1 i ← 1

while (i <= N) do if (find(Child1 == P1(i)))

value ← P1(i)

while find(Child1 == value!=0) do location ← find(Child1 == P1(i))

value ← Child2 (location)

end while

Child1(i) ← Child2(location)

else Child1(i) ← P1(i)

end if end while

%Similarly child2 from P2%

%For Child3

i ← 1

while (i <= N) do if (find(Child3 == P1(i)))

value ← P1(i)

while find(P2 == value!=0) do location ← find(P2 == value) value ← P2 (location)

end while

Child3(i) ← P2(location)

else

Child3(i) ← P1(i)

end if end while

%Similarly child4%

• V.    Performance Evaluation

In this research, we have conducted a simulation study to determine and examine the performance of mo- PMX along with other competitive operators according to various parameters such as average and standard deviation (S.D). In Section V(A), the testing methodology for this study is discussed and simulation results with discussion are presented in Section V(B).

• A.    Computational testing methodology

  To analyze the performances of the MO-PMX, computational experiments have been performed by using eighteen benchmark instances which are taken from the traveling salesman problem library (TSPLIB) [28]. The test benchmarks are Euclidean, twodimensional symmetric and asymmetric problems within 14 to 532 cities. All GA programs were implemented in this simulation study through MATLAB version R2017a. Fundamentally, GAs use operators in such a way that they preserve beneficial information, keeping in view the goal of exploring the better solution. The least distance of any TSP is the objective function, which permits the GA to retain the better solutions and inhibit others. Table 1 shows the parameter values of the GA which are used in this study.

Table 1. Parametric configuration for GA

Parameter description	Value
Population size (N)	200
Selection operator	Tournament
Crossover probability ( P c )	100%
Mutation operator	Exchange
Mutation probability (Pm)	20%
Maximum generation	5000
Number of runs	30
Replacement in GA	Steady-state
GA Replacement percentage	4% to 10%

Since GA belongs to the class of probabilistic search techniques, we use the two-sampled pooled t-test as a statistical hypothesis testing [29,30]. The experiments were performed in 30 independent trials (each pair of n1 = n2 = 30) for each instance to achieve a comparable solution. In this study, we set our null hypothesis in the following way: ‘MO-PMX convergences at least as fast as other operators in comparison’. Throughout this study, all the statistical differences are shown at p = 0.05 (95% confidence) level of significance by using the two-sample pooled t-test. The two-tailed t-test value indicates whether a significant improvement by MO-PMX (t ≤ -2.00) or significant degradation by MO-PMX (t ≥ 2.00).

But within the range (-2.00< t < 2.00) of two-tailed t-test score do not reflect the reasonable statistical evidence to confirm or refute our null hypothesis, which indicates that there is no statistical significance between the two approaches.

Table 2. Comparison of crossover schemes with respect to average, S.D and t-test values for TSPs

	Instance	burma14	gr21	bayg29	dantzig42	eil76	eil101	brg180	pr226	att532
	Average	3331	2822	1648	752	558	652	2058	82464	29854
OX	S.D	8	72	12	20	18	17	93	243	517
	t-test	-3.42	-5.93	-7.24	-6.64	-3.48	-4.01	-3.59	-20.45	-13.88
MO-	Average	3328	2762	1633	739	552	644	2019	81832	28637
GA	S.D	6	31	10	17	14	10	58	190	513
	t-test	-2.06	-3.26	-2.28	-4.44	-2.26	-2.52	-2.16	-10.6	-4.77
	Average	3342	2829	1639	761	587	647	2087	82893	30812
CX	S.D	12	49	17	35	17	16	75	423	671
	t-test	-7.04	-9.12	-3.28	-5.81	-11.76	-3.31	-6.3	-18.47	-18.1
	Average	3340	2818	1657	735	582	669	2071	82667	29978
CX2	S.D	10	38	31	17	21	22	82	229	528
	t-test	-7.22	-9.89	-4.96	-3.59	-8.72	-7.13	-4.83	-24.99	-14.65
	Average	3334	2854	1649	748	562	646	2048	82690	29712
PMX	S.D	11	57	20	23	15	9	72	365	469
	t-test	-4.01	-10.22	-5.3	-5.42	-5.23	-3.57	-3.82	-18.17	-13.45
	Average	3325	2740	1627	718	545	638	1993	81318	28004
MO- PMX	S.D	5	19	10	19	9	8	29	179	498
	t-test	-	-	-	-	-	-	-	-	-

Table 3. Comparison of crossover schemes with respect to average, S.D and t-test values for ATSPs

	Instance	br17	ftv33	ftv38	p43	ft53	ftv170	rbg323	rbg358	rbg443
	Average	39	1407	1687	5862	7432	3138	1817	1412	3614
OX	S.D	0	93	68	102	162	215	175	140	152
	t-test	0	-3.46	-4.94	-4.85	-5.26	-5.69	-9.04	-3.92	-10.16
	Average	39	1377	1650	5795	7298	2966	1599	1358	3320
MO-GA	S.D	0	88	89	67	189	158	160	147	114
	t-test	0	-2.05	-2.15	-2.32	-2.09	-2.4	-3.91	-2.17	-2.41
	Average	41	1429	1658	5847	7714	3076	1824	1469	3814
CX	S.D	1	82	84	67	140	209	162	191	197
	t-test	-10.77	-4.96	-2.83	-5.57	-12.29	-4.42	-9.66	-4.55	-13.19
	Average	39	1391	1664	5891	7704	3119	1799	1497	3792
CX2	S.D	0	102	89	91	208	169	154	204	108
	t-test	0	-2.49	-2.89	-6.77	-9.97	-6.25	-9.29	-4.98	-18
	Average	39	1441	1678	5798	7417	3093	1778	1423	3652
PMX	S.D	0	89	75	83	169	210	180	118	159
	t-test	0	-5.3	-4.1	-2.18	-4.83	-4.79	-7.94	-4.73	-10.9
	Average	39	1337	1609	5758	7197	2877	1448	1286	3248
MO-PMX	S.D	0	57	51	54	178	122	133	102	123
	t-test	-	-	-	-	-	-	-	-	-

• B.    Simulation results and discussion

To compare the efficiency of various crossover operators including OX, MO-GA, CX, CX2, PMX and the proposed one (MO-PMX) with the help of MATLAB software. At first, we divide the benchmark instances into two parts as symmetric traveling salesman problems (TSPs) and asymmetric traveling salesman problems (ATSPs). These benchmarks are arranged in the ascending order of nodes and quality of the solution is studied for the purpose of performance evaluation of all six crossover operators.

Table 2 summarizes the results of nine symmetric TSP problems of size 14 to 532 for six competing crossover operators with BTS and EM as selection and mutation schemes respectively. Results are compared on the basis of average and standard deviation (S.D) for each crossover scheme to testing the benchmarks with the objective to minimize the total travel distance. The significant improvements in the performance of MO-PMX with respect to other approaches are indicated by two-tailed t-test values. According to the critical value (t = - 2.00), all computed t-values are less than -2.00 (bold values) for all nine benchmark instances and have shown the significantly improved performance by the proposed operator. In other words, the simulation results found by the MO-PMX are statistically significantly better than the solution quality found by the other five crossover approaches (OX, MO-GA, CX, CX2 and PMX) for all used test problems.

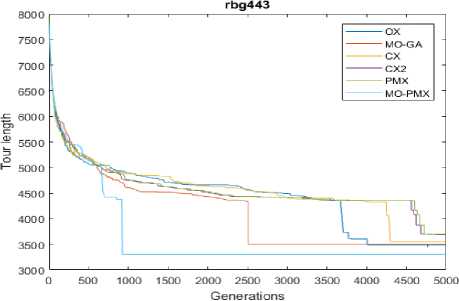
Fig.2. Convergence of GA using various crossover operators on the instance rbg443

We continue this study for various asymmetric TSPLIB (ATSPs) instances, which are reported in Table 3 . This elaborates the results according to average, S.D and two-tailed t-test for nine instances of size 17 to 443. The t-test values indicate that the proposed operator MO-PMX has a significantly better solution quality when compared to other traditional crossover operators (OX, MO-GA, CX, CX2 and PMX). In the other visual analysis, we can clearly see from Fig. 2., which depicts the convergence of MO-PMX for the best optimal tour found in 30 independent runs for the instance “rbg443”. All the results which are presented in this section suggest that the proposed MO-PMX scheme enables the GA to find better solution quality to solve the combinatorial optimization problems.

• VI.    Conclusions

This research presents a comprehensive overview of the performance of GAs in NP-hard problems like TSP and keenly observes how GAs create a solution without having any prior knowledge about the traveling routes. Unlike other heuristic methods, GA uses natural rules of selection, crossover and mutation operators to make the computation easier and fast. These operators make it more valuable, better performing and efficient algorithm over other meta-heuristic algorithms. Various crossover operators have been introduced for TSP by using GAs. We also proposed a new crossover scheme for TSP which is an upgraded version of the path-represented PMX operator. It generates multi-offspring which shows that it can efficiently increase the search ability of the algorithm by producing multiple possible solutions. Eighteen benchmarks from the TSPLIB have been used and simulation experiments were carried out to asses the effectiveness of the MO-PMX over other conventional crossover operators. For comparison and to investigate that how they converge on the basis of average values and also observed their accuracy in the results in different runs with the help of an absolute measure S.D. The significance of such improvement is also validated through a two-tailed t-test. Hence the proposed operator might be a good candidate to get accurate convergent results. Moreover, researchers might be more confident to apply it for comparisons.