Development of a model of management of organizational system of industrial enterprise for optimization of production of custom products

                                          том 21 № 1 (66), 2025, ст. 6

• I.    Classification of models and methods of custom production management

The present article focuses on the development of a universal model for managing single-unit production based on enterprise data. For this purpose, the article provides an analysis of existing models and algorithms to identify the most successful practices, as well as to highlight important variables and constraints that need to be considered when developing the model. The creation of an effective management model based on enterprise data will minimize potential losses and optimize production operations, while enabling the production of non-standard items without detriment to serial manufacturing. To standardize the models and methods of management, a classification into four main categories was proposed: management methods (MGM), mathematical planning methods (MP), methods for individual system elements (ME), complex automation solutions (CAS).

• A.    Management methods

One of the popular practices of production optimization is the method of lean production, which can also be used at enterprises with unit production [1, 2]. Lean manufacturing helps reduce waste and streamline processes, making it particularly effective for small-batch production where flexibility and efficiency are critical.

• B.    Mathematical methods

• C.    Models and methods for individual elements of the system (IM)

• D.    Brandl [6] proposes using design patterns that help in fast equipment changeover and reprofiling of production processes. His approach relies on network models and graphs, linear programming methods, stochastic models and discrete event models. Yuriev V.N. [7] in his study describes a mathematical model for calculating raw material requirements in order-by-order production. This model ensures timely fulfillment of operational production tasks with minimal costs. Other authors [8] use methods of simulation modeling, describing variants of technological process development on the example of production of one type of single part.

• D.    Сomplex automation solutions (CAS)

PLM and ERP systems are popular among complex automation solutions [9]. The complexity of implementing such systems at enterprises with single or small batch production lies in the need to adapt these systems to high variability of orders, uniqueness of products and frequent changes in production processes, which requires significant costs for customization, complicates integration with existing processes and increases the requirements for staff qualification.

• E.    Comparison of groups of methods

We can compare these groups of methods in more detail in Table 1.

Table 1. Comparison of the methods

Group of methods	Implementation complexity	Advantages	Disadvantages
MGM	Medium	Identification and classification of problems, improved control	Employee resistance, need for continuous monitoring
MP	High	Bottleneck prevention, increased planning accuracy, workload balancing	Highly sensitive to data quality, difficult to adapt to dynamic changes
ME	Medium	Flexibility in process adaptation, ability to test various scenarios	Limited applicability without a comprehensive approach, need for detailed model development
CAS	Very high	Increased process transparency, reduced decision-making time, data integration	High costs, complexity of implementation and integration, need for skilled specialists

Analysis of production optimization methods shows that each has strengths and limitations. Management methods reduce waste but lack order-specific focus. Mathematical planning ensures precision but requires time and expertise. System element models optimize specific processes but have limited scope, while automation solutions offer full integration at a high cost. In unit or small-batch production, adapting to order needs and workforce skills is crucial but often overlooked. A mathematical production planning model based on order data and team competencies could combine these advantages, improving flexibility, accuracy, and efficiency.

• II.    Problem statement

The analysis in Section I shows that a universal single-unit production model should combine the best practices from all categories. An integrated approach allows enterprises to adapt, stay competitive, and quickly respond to customer demands and production changes.

To achieve the stated objective, it is essential to clearly define the management task and identify specific actions required. The task must be described with sufficient clarity to avoid ambiguity and ensure practical applicability.

The object of management in this context comprises business processes aimed at producing custom and small-batch items according to technical specifications and customer requirements.

• F.    Audit of production processes

As part of the analysis of single-unit and small-batch production enterprises, an initial audit was conducted at a factory specializing in technologically complex equipment for the food industry.

The enterprise uniquely combines single-unit, small-batch, and serial production. The factory employs over 180 employees, and its organizational structure is shown in Figure 1.

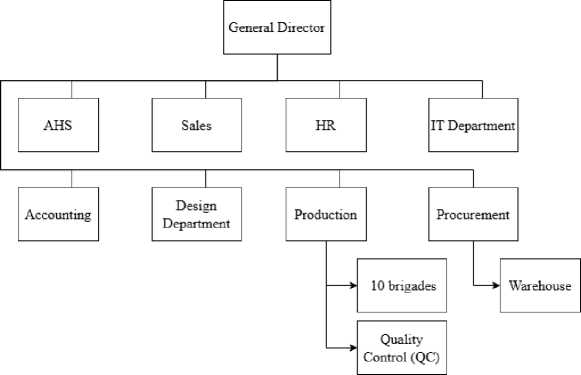
Fig. 1. Organizational structure

During the audit, the following key features of the production process were identified:

• Production Planning. The plant operates according to a quarterly production plan. It is formed by the production manager on the basis of orders received using expert evaluation methods. This takes into account capacity constraints, supply chain constraints and team skills. The plant has resorted to this method of planning due to increased demand for products and the impossibility of setting precise deadlines.

• •    Workshop organizational structure. The production workshop operates under a team-based structure and includes: 8 assembly teams, 1 electrical installation team, 1 milling team, 1 quality control and 1 preparation team. Thus the areas of the locksmith and turning area and the painting area are the bottlenecks of production. It is important to note that the teams have different qualifications for the manufacture of certain types of products. At the same time, the transition of one team from the manufacture of one type of product to another can significantly reduce the productivity of the site. And the appearance of a batch of a new small batch product can reduce productivity by up to 30-40%.

• •    Cost Drivers. The primary factors influencing product cost are material costs with its delivery to the production site and labor expenses.

The audit identified critical limitations and challenges in the plant's operations. Production planning is conducted quarterly using expert evaluation methods. Despite considering capacity constraints, supply chain limitations, and team skills, this approach remains subjective and imprecise due to increased demand and the inability to establish exact deadlines. The workshop's team-based structure encounters bottlenecks in the locksmith, turning, and painting areas. Significant productivity losses of up to 30-40% are observed during transitions between product types or when handling new small-batch orders due to varying team qualifications. Furthermore, material costs, including delivery expenses, and labor expenses are the primary cost drivers significantly influencing overall product costs.

• G.    Audit of production processes

Based on the analysis of existing models and the audit results, a new approach is needed to manage unit and small-batch production effectively. Traditional methods lack flexibility and adaptability, while the audit revealed inefficiencies, bottlenecks, and high dependency on material and labor costs.

To address these issues, an optimization model is proposed to maximize productivity while considering resource, time, and budget constraints. The core of this formulation is the objective function Q(x), which represents a generalized metric for evaluating system performance.

The objective function Q(x) is designed to maximize efficiency of custom and small batch production.

It integrates key parameters which were conducted as important according to models' analysis and audit. For example, cycle time, labor resource utilization, equipment productivity, and other critical factors that influence the performance of the production system. The variables influencing Q(x) are represented by vector X :

X = {LRU, CT, ES, TD CP}                                                    (1)

The components of the vector are presented in Table 2.

Table 2. System performance function parameters

Name of the parameter	Explanation
LRU (Labor Resource Utilization)	the proportion of productive working time for employees
CT ( Cycle Time)	the average time required to complete one order
ES (Employee Skills)	the average qualification level of workers involved in production
TD (Training Duration)	the time required to train personnel for new tasks
CP (Cost per Product)	the production cost of a single unit

To ensure practical feasibility, the optimization problem is subject to a set of constraints D , defined as:

D = {D bud , D

tmax , D cap , D hr , D wtmax , D trmax ,

D lead , D util }

Where the constraints are:

• •   D bud : Maximum available budget for development, implementation, and support ;

• •   D tmax : Maximum allowable time for implementing changes;

• •    D cap : Maximum available capital resources;

• •   D hr : Maximum availability of personnel

• •   D wtmax : Maximum weekly working hours per employee;

• •    D trmax : Maximum allowable training duration;

• •   D util : Maximum productive equipment utilization time.

• •    D lead : Maximum allowable order lead time

The optimization problem is then formulated as:

max Q(x) = f(x)                                                                      (3)

The formulation of the management problem establishes a foundation for addressing inefficiencies identified in the literature review and production audit by defining an objective function and key variables under practical constraints like budget, time, and resources. This structured approach highlights the need for a systematic solution capable of optimizing complex production processes. Consequently, developing a mathematical model becomes essential to integrate these variables into a unified framework, enabling precise and adaptable production planning.

• III.    Model of management of the production plan with small batch manufacturing

• H.    Justifiaction of the model

Based on the results of the management problem formulation and the initial audit of production business processes, it was decided to develop a mathematical model for creating an optimal quarterly production plan. The absence of systematic planning can lead to overloading of production capacities, resulting in extended order fulfillment times and breaches of client obligations. Additionally, this causes inefficient resource allocation, including materials and labor, leading to idle time or excessive inventory. Under these conditions, the risk of increased product costs and reduced quality due to rushed order execution rises, negatively impacting the company’s competitiveness. To address these issues, a mathematical planning model is proposed to optimize resource utilization, minimize idle time, and enhance productivity.

• I.    Model description and key parameters

The model integrates key variables that influence overall productivity, including team skills, workload distribution, and production bottlenecks. These variables are defined as follows:

• S i :    Team Skills. The ability of each team to produce specific types of products. For each team, the range of products they can manufacture is defined.

W i : The current workload of each team, including overtime, work schedules, and days off. This variable limits available time resources and impacts task allocation.

K ij : Qualification Level. The skill level of each team for producing product type i .

Q j : The number of units of each product type to be manufactured over a three-month period.

L k : Workshop Capacity. The state of production capacities, where k indicates a specific workshop or area (e.g., locksmithing). The productivity of other areas depends on the throughput of this bottleneck.

R ij : Reprofiling Costs. The time required for a team to transition from producing product type i to another type j. Transition times are shorter for technologically similar products.

These variables capture the complexities of unit and small-batch production, ensuring that the model reflects real-world conditions and operational constraints. The objective function Z of the model is the maximization of unit and small batch productivity, which depends on the specified parameters. It is defined as follows:

Z =f {S i , W i , K ij , Q j , L k , R ij } (4) J. Appropriate methods

The proposed mathematical model addresses the complexities of unit and small-batch production, which require a combination of optimization and simulation techniques to handle constraints such as resource allocation, workload distribution, and production bottlenecks. The choice of methods is driven by the need to balance precision, adaptability, and computational efficiency while ensuring that the model can be practically implemented in real-world production environments. Based on these considerations, the following methods are proposed as potential solutions for implementing the model.

Linear Programming optimizes the distribution of batch sizes among teams, ensuring efficient resource allocation while minimizing idle time and respecting constraints like team qualifications and workload limits. Combinatorial Optimization reduces retooling time by prioritizing the sequential production of similar products during task transitions. Simulation Modeling identifies bottlenecks, evaluates alternative scenarios, and adjusts parameters to ensure robustness under real-world fluctuations.

K. Future implementation and testing

The practical implementation of the proposed model is planned for the next phase of the study. The model can be implemented using specialized optimization and simulation tools. For linear programming, Python libraries such as PuLP or commercial solvers like Gurobi are highly effective for resource allocation tasks. Combinatorial optimization can be performed using Google OR-Tools, which supports task sequencing and transition scheduling. For simulation modeling, AnyLogic or MATLAB Simulink are recommended to test the model under dynamic production conditions and evaluate its robustness. In the near future, the authors plan to implement the proposed model using real-world data collected from the enterprise under study. This implementation will involve gathering detailed operational data, including team schedules, qualification levels, workload distributions, and production capacities across various workshops. The collected dataset will serve as the foundation for testing and validating the model's performance in a practical setting.

To ensure transparency and contribute to the research community, the authors intend to share the compiled dataset along with the results obtained from its analysis. By making the data publicly available, the study aims to facilitate further research and enable other researchers to validate or extend the proposed approach. The results of the model's application will be compared against the traditional quarterly production planning methods currently employed by the enterprise to evaluate its effectiveness in enhancing productivity and adaptability. This planned implementation not only aims to demonstrate the practical applicability of the model but also to provide actionable insights for improving unit and small-batch manufacturing processes in real-world industrial environments.

• IV.    Conclusion

This study addressed the challenges of unit and small-batch production in modern manufacturing environments by proposing a mathematical model for optimizing production planning. Through a comprehensive analysis of existing literature and the audit of a real-world enterprise, key inefficiencies were identified, including resource bottlenecks, suboptimal task allocation, and the lack of systematic planning methods. The proposed model incorporates critical variables such as team skills, workload distribution, batch sizes, and transition times, and leverages optimization techniques like linear programming, combinatorial optimization, and simulation modeling to enhance productivity and adaptability. Future implementation using real-world enterprise data will validate the model's effectiveness, with plans to share the collected dataset and results to support further research. This work contributes to improving production efficiency in small-batch manufacturing, offering a practical framework for addressing operational complexities.