Дезагрегированный подход к моделированию индекса потребительских цен: региональный аспект

DOI:

Моделирование инфляционных процессов представляет собой важнейший инструмент экономического анализа и прогнозирования, позволяющий оценивать динамику цен, предвидеть макроэкономические риски и корректировать направления денежно-кредитной политики. Инфляция оказывает непосредственное влияние на уровень жизни населения, инвестиционную активность бизнеса и стабильность финансовой системы, что делает ее прогноз критически значимым как для государственных экономических институтов, так и для частного сектора.

Особую сложность представляет региональное прогнозирование важного критерия инфляции – индекса потребительских цен, поскольку ценовая динамика в субъектах Федерации существенно отличается от общероссийской из-за различий в структуре потребления, локальных экономических условий и внешних шоков. Традиционные подходы, основанные на агрегированных показателях, зачастую не учитывают эту неодно- родность, что снижает точность прогнозов. В связи с этим применение современных методов машинного обучения и многоуровневого моделирования ИПЦ позволяет не только повысить качество предсказаний, но и выявить ключевые факторы инфляции на уровне отдельных товарных групп.

Данное исследование направлено на разработку методики дезагрегированного прогнозирования ИПЦ с использованием алгоритмов SARIMA, Prophet, Ridge regression, Random Forest и CatBoost, а также оценку влияния различных уровней детализации данных на точность моделей.

Обзор литературы

Прогнозирование инфляции остается одной из ключевых задач экономической науки и практики, особенно в условиях нестабильности мировых рынков и сохранения региональных дисбалансов. Точные прогнозы позволяют центральным банкам корректировать денежно-кредитную политику, бизнесу – планировать стратегии, правительству – разрабатывать антиинфляционные меры.

Вместе с тем большинство работ, посвященных моделированию инфляции, имеют общую черту: в качестве искомой переменной выступает только индекс потребительских цен по группе «Все товары и услуги», так называемая инфляция в целом.

В экономической литературе существуют разные подходы к прогнозированию ИПЦ. Так, для предсказания годовых темпов инфляции инструментами машинного обучения У. Джункеев [Джункеев, 2024] применил модели градиентного бустинга, решающих деревьев, сверточную и рекурентную нейронные сети (CNN, RNN). В качестве эндогенной переменной автор использовал ИПЦ в процентах к соответствующему месяцу предыдущего года (г/г). Аналогичного подхода придерживались Е. Павлов [Павлов, 2020] и И. Байбуза [Байбуза, 2018].

Е. Волгина в своих исследованиях также применила модели машинного обучения и нейронные сети [Волгина, 2025]. В качестве эндогенной переменной автор использовала тот же ИПЦ в процентах, но помесячно (м/м). Отличительной особенностью работы является введение дополнительного фактора – тональности СМИ.

О. Семитуркин и А. Шевелев также моделировали инфляцию в месячном выражении, но уже на региональном уровне – по макрорегиону Сибирь [Семитуркин, Шевелев, 2023]. В качестве инструментария авторы использовали ML-модели и нейронные сети.

Традиционные методы обычно фокусируются на агрегированных показателях инфляции, однако покомпонентный подход, предполагающий анализ отдельных составляющих индекса потребительских цен, приобретает все большую популярность благодаря своей потенциальной точности и информативности, что подтверждают результаты исследований В. Крамкова [Крамков, 2023], который в качестве эндогенных переменных использует 3 компонента (продовольственные, непродовольственные товары и услуги), 6 компонент (отдельно выделены плодоовощная продукция, топливо моторное и услуги ЖКХ), 18 компонент (выделены еще несколько наиболее весомых и/или волатильных товарных групп) и 45 компонент. Аналогичные результаты представлены в работе Р. Латыпова, Е. Ахмедовой, Е. Постолита и М. Микитчук [Латыпов и др., 2024], где авторы используют разложение ИПЦ на 80 компонентов.

Анализ публикаций свидетельствует, что некоторые ученые для моделирования инфляции опираются на различные архитектуры нейронных сетей. Для целей настоящего исследования их применение мы посчитали нецелесообразным ввиду недостаточного количества точек для качественного обучения модели, даже на нескольких эпохах: согласно Е. Choi с соавторами, для достижения хорошей производительности RNN требуется минимум 1 000–2 000 наблюдений (83 года с помесячными данными); их число зависит от сложности задачи и специфики данных; на практике зачастую выстраиваются более длинные ряды – от 5 000 наблюдений [Choi et al., 2016].

Кроме того, как отмечают M. Mamedli и D. Shibitov [Mamedli, Shibitov, 2021], при построении прогноза важно учитывать задержки в публикации макроэкономических данных: например, показатели промышленного производства за определенный месяц становятся доступными лишь в начале, а данные по инфляции – в середине следующего месяца. Игнорирование этих лагов может привести к переоценке точности прогноза. В нашей работе данный эффект учитывается, что позволяет получить оценки вневыборочной ошибки, в большей мере соответствующие условиям реального прогнозирования инфляции.

Методология исследования

В целях построения прогноза месячного индекса потребительских цен (ИПЦ) на региональном уровне (в Ставропольском крае) были использованы различные модели временных рядов и алгоритмы машинного обучения:

• 1)    SARIMA (Seasonal ARIMA);

• 2)    Prophet;

• 3)    Ridge regression (регрессия с L2-регуля-ризацией);

• 4)    Random Forest Regression;

• 5)    CatBoost Regressor.

Модель SARIMA представляет собой расширение классической модели ARIMA с учетом сезонных колебаний. Ее обобщенная форма записывается следующим образом [Box et al., 2015]:

Фр(В) * ®p(BS) * (1 - B)d * (1 - Bs)Dyt = = eq(B)*eQ(Bs)*st, где Фр(В) и θq(B) – полиномы операторов авторегрессии и скользящего среднего; Фр(ВS) и θQ(BS) – полиномы сезонной авторегрессии и сезонного скользящего среднего; B – оператор сдвига назад: By= yt–1; d и D – порядок обычного (несезонного) дифференцирования временного ряда; S – длина сезонного периода; yt – наблюдаемое значение временного ряда в момент времени t; εt – белый шум (случайная ошибка).

Prophet – метод прогнозирования временных рядов, разработанный Facebook, ориентированный на данные с выраженной сезонностью и праздничными эффектами. Он основан на аддитивной декомпозиции, представлен следующей формой:

• –    тренд (Trend): используется два типа трендов: линейный и логарифмический (с ограничением сверху), который подстраивается под данные и может меняться во времени;

• –    сезонность (Seasonality): учитывается как годовая сезонность, так и дополнительные сезонные колебания (еженедельные или ежемесячные циклы);

• –    праздники (Holidays): позволяет учитывать влияние праздников и других специальных событий на временной ряд, например, продажи в праздничные дни;

  – ошибки (Residuals): остатки модели предполагаются случайными, и их можно моделировать с использованием нормального распределения или других подходов для оценки неопределенности.

Математическая форма модели Prophet выглядит следующим образом [Taylor, Letham, 2017]:

y(0 = ^(0 + ^(0 + Ш) + Et, (2)

где y ( t ) – наблюдаемое значение во времени t ; g ( t ) – тренд; s ( t ) – сезонность; h ( t ) – влияние праздников и специальных событий; ε _t – случайная ошибка.

Метод Ridge regression , также известный как L2-регрессия, представляет собой разновидность линейной регрессии, включающую в себя регуляризацию для улучшения качества модели и предотвращения переобучения.

В классической линейной регрессии модель определяется уравнением:

y = X β + ε, (3)

где y – вектор наблюдаемых признаков; X – матрица признаков; β – вектор коэффициентов модели; ε – ошибка модели.

Метод находит такие значения коэффициентов β, которые минимизируют сумму квадратов ошибок. Однако при большом количестве признаков или наличии мультиколлинеарности коэффициенты модели могут становиться нестабиль- ными и чрезмерно чувствительными к незначительным изменениям в данных, что приводит к переобучению. Метод Ridge regression вводит дополнительный штраф за величину коэффициентов, что позволяет уменьшить их влияние на модель и улучшить обобщающую способность. Модифицированная цель оптимизации с L2-регу-ляризацией выглядит следующим образом [Bishop, 2006; James et al., 2013]:

bridge = argmin_p(\\y - Xp\\² + Л||^||²),(4) где λ – параметр регуляризации (гиперпараметр), который контролирует величину штрафа; IIZOI² – сумма квадратов коэффициентов.

Метод Random Forest (случайный лес) создает несколько деревьев на основе случайно выбранных подмножеств данных и случайных признаков, используемых для построения каждого дерева. Для прогнозирования модель агрегирует результаты всех деревьев. Для задачи регрессии используется усреднение прогнозов [Breiman, 2001; Liaw, Wiener, 2002].

CatBoost (градиентный бустинг) позволяет строить аддитивную функцию в виде суммы деревьев решений итерационно, по аналогии с методом градиентного спуска [Dorogush, Ershov, Gulin, 2017]. Его основной идеей является устранение ошибок предыдущего шага. Обобщенный алгоритм его работы предполагает определение набора данных {(^-УЭ}д = 1..... n ; числа итераций M ; выбор функции потерь L ( y , f ) с выписанным градиентом; выбор семейства функций базовых алгоритмов h ( x , θ), с процедурой их обучения; определение дополнительных гиперпараметров h ( x , θ), например, глубины дерева у дерева решений [Prokhorenkova et al., 2019].

Затем проводится инициализация модели градиентного бустинга константным значением ^:

% = argminX^L (y,, y),         (5)

где n – количество обучающих примеров (объектов).

После чего для каждой итерации t = 1, ... , M повторяется ряд действий:

• 1)    определение псевдо-остатков r_t :

  8L(yi'f(xS)

  
  

  Sf^Xi}

  
  

  ^(x^fM

  
  

  '^{i = 1}.....", (6)

  
  

где δ – частная производная функции потерь по предсказанию модели;

• 2)    построение нового базового алгоритма h_t ( x ) на псевдо-остатках {( x_i, r_it )} _{i = 1,…, n} ;

• 3)    поиск оптимального коэффициента ρ_t при h_t(x) относительно исходной функции потерь:

Pt = argmin ^^(у^х) + P * h^.Q)} , (7)

• 4)    сохранение ftM = PtMtM .

После этого формируется итоговая GBM-модель :

ГМ^ЛЫ .      (8)

В качестве исходных данных для проведения исследования выступила информация об индексе потребительских цен в Ставропольском крае и России в целом в месячном выражении (далее – ИПЦ, MoM 2) по 82 компонентам инфляции: ИПЦ, MoM в целом («Все товары и услуги») (1-й уровень), компоненты «Продовольственные товары», «Непродовольственные товары» («Услуги») (2-й уровень) и 78 основных товарных групп (3-й уровень).

В качестве регрессоров выбраны следующие группы факторов: 1) статистические данные Росстата, характеризующие социально-экономическое положение субъектов Российской Федерации; 2) курс доллара в среднем за месяц 3; 3) индекс ММВБ в среднем за месяц; 4) данные мониторинга предприятий Банка России; 5) динамика банковского кредитования и привлечения средств клиентов. Таким образом, в итоговый набор экзогенных переменных без учета лаго-вой структуры вошли более 60 показателей.

Отметим, что в настоящем исследовании мы не используем сезонно-скорректированный таргет (индекс потребительских цен и его компоненты), поскольку его применение может исказить как интерпретацию результатов, так и сам процесс прогнозирования. По нашему мнению, сглаживание сезонной компоненты до этапа моделирования фактически лишает модель возможности учитывать повторяющиеся закономерности, присущие временным рядам. Кроме того, сезонная коррекция предполагает наличие априорного знания о структуре сезонности, тогда как в реальных условиях сезонные колебания могут быть нестабильными и изменяться со временем. Важно также отметить, что прогноз в модели, обученной на скорректированном таргете, требует последующего восстановления сезонной компоненты, что влечет дополнительные источники ошибки. Следовательно, в таком случае присутствует искусственное завышение качества модели, которое нивелируется при восстановлении сезонно-скорректированного ряда. Поскольку в прикладных задачах, как правило, интерес представляют именно фактические (нескорректированные) значения, использование оригинального ИПЦ позволяет получать более реалистичные оценки и отражает поведение показателя в будущем.

Очевидно, что региональные экономики в едином национальном пространстве функционируют в условиях высокой степени открытости, иными словами, продукция, произведенная в одном субъекте России, свободно перемещается и реализуется на рынках других регионов. Это свидетельствует о том, что объем производства товаров в регионе не всегда коррелирует с уровнем цен на данной территории и в ряде случаев может не оказывать на него существенного влияния. В этой связи в исследовании использованы экзогенные переменные как по Ставропольскому краю, так и в целом по Российской Федерации.

Непосредственно для моделирования исходная выборка разделена на обучающую (train) и тестовую (test) части.

Важно отметить, что тренировочная выборка по ИПЦ и его компонентам включает период с января 2010 г. по декабрь 2023 года. При этом для экзогенных переменных – с января 2009 г. по сентябрь 2023 г. включительно. Такое отличие в периодичности от таргета необходимо для учета лаговой структуры в процессе моделирования.

Тестовая часть не задействована в обучении моделей и их валидации, а используется исключительно для оценки прогностических свойств модели. В качестве тестового периода рассматривались последовательно расширяющиеся временные интервалы в пределах 2024 г., а именно: январь – март (1–3 месяца), январь – июнь (1–6 месяцев), январь – сентябрь (1–9 месяцев), январь – декабрь (1–12 месяцев).

Обучение моделей осуществлялось с использованием процедуры кросс-валидации с тремя фолдами, что обеспечивало устойчивую оценку их прогностических характеристик и позволяло выбрать наилучшую модель для прогнозирования отдельных компонент индекса потребительских цен (ИПЦ) в помесячной динамике (MoM) на различных горизонтах прогнозирования.

Важным элементом методики явилось требование предварительной известности всех экзогенных переменных, используемых в моделях. В частности, при построении прогноза на h месяцев вперед все экзогенные переменные включались в модель с минимальным лагом не менее h месяцев, что исключало использование информации «из будущего» (табл. 1).

Прогнозирование индекса потребительских цен (ИПЦ) осуществлялось поэтапно, с использованием трех уровней агрегирования, отражающих различные степени детализации:

• 1)    Моделирование агрегированного ИПЦ – построение прогноза непосредственно по совокупному индексу, без предварительного разложения на составляющие компоненты.

• 2)    Моделирование укрупненных компонент – прогнозирование по трем основным категориям: «Продовольственные товары», «Непродовольственные товары» и «Услуги». Последующее агрегирование общего значения ИПЦ осуществлялось посредством взвешенного суммирования прогнозных значений указанных категорий с использованием официальных весов, опубликованных Федеральной службой государственной статистики (Росстат) на 2024 год.

• 3)    Моделирование на уровне 78 товарных групп – прогнозирование по каждому из субкомпонент ИПЦ, включающих товары и услуги. Итоговое значение индекса формировалось путем агрегирования прогнозов с учетом соответствующих весов, отражающих структуру потребительской корзины.

Для каждого прогнозного горизонта (1, 3, 6, 9 и 12 месяцев) производился отбор наилучшей модели на основе процедуры трехфолдовой кроссвалидации. Выбор модели осуществлялся отдельно для каждого уровня детализации (агрегированный, укрупненный и детализированный уровни), что обеспечивало адаптивность подхода к различным аспектам динамики потребительских цен.

Методические подходы к моделированию

Перед подачей данных на вход прогнозным моделям все числовые переменные были стандартизированы с использованием метода StandardScaler, обеспечивающего приведение значений признаков к единой шкале. Для линейных моделей дополнительно проведена проверка временных рядов на стационарность с применением теста Дики – Фуллера. Все нестационарные ряды преобразованы методом первых разниц.

Для повышения вычислительной эффективности и сокращения времени обучения моделей размерность пространства экзогенных переменных снижена методом главных компонент ( PCA ). Данный метод позволяет трансформировать исходный набор коррелированных признаков в ограниченное число новых ортогональных переменных – главных компонент, которые упорядочиваются по степени объясняемой дисперсии [Ringnér, 2008].

В настоящем исследовании сохраненный набор компонент объяснял не менее 95 % дисперсии исходных данных. При моделировании ИПЦ на горизонте 12 месяцев с учетом лагов было получено свыше 600 предикторов, их удалось сократить до 75 компонент без существенной потери качества (см. рис. 1).

Поскольку не все предикторы вносят значимый вклад в формирование ИПЦ и его компонент, для отбора наиболее информативных признаков применялся алгоритм Recursive Feature Elimination (RFE). Этот метод итеративно исключает наименее значимые признаки на основе внутренних оценок важности модели (например, коэффициентов регрессии или важности признаков в деревьях решений), до достижения заданного числа признаков [Kuhn, Johnson, 2013; Pedregosa et al., 2011].

Для повышения качества прогнозов, приближенных к условиям реального времени, отбор оптимальных моделей для каждого прогностического горизонта и компоненты ИПЦ осуществлялся на основе трехфолдовой кросс-валидации.

Дополнительно проводилась настройка гиперпараметров моделей при помощи процедуры GridSearchCV из библиотеки scikit-learn, обеспечивающей перебор заданных комбинаций пара-

Таблица 1

Прогнозные горизонты и используемые лаги экзогенных переменных

Период прогноза	Лаги
1–3 месяца	3–12
4–6 месяцев	6–12
7–9 месяцев	9–12
9–12 месяцев	12

Примечание. Составлено авторами.

метров и оценку результатов на основе кроссвалидации. В качестве целевой метрики использовалась средняя абсолютная ошибка (MAE).

Подбор гиперпараметров с помощью GridSearchCV (кроме SARIMA и Prophet) осуществлялся отдельно для каждой из следующих моделей 4:

• 1.    Модель SARIMA характеризуется набором гиперпараметров, определяющих ее структуру: p , d , q – порядки авторегрессии, интегрирования (дифференцирования) и скользящего среднего соответственно; P , D , Q – их сезонные аналоги с периодом сезонности s . Эти параметры не обучаются напрямую, а подбираются до построения модели, поскольку определяют конфигурацию временного ряда, включая тренды, сезонные колебания и шум.

• 2.    Модель Prophet имеет ряд гиперпараметров, регулирующих ее поведение и степень адаптации к данным временного ряда. Ключевыми из них являются: changepoint_prior_scale – управляет чувствительностью модели к изменениям тренда; seasonality_prior_scale – регулирует силу сезонной компоненты; seasonality_mode – определяет тип сезонности (аддитивная или мультипликативная); n_changepoints – задает число возможных точек смены тренда.

• 3.    Ridge Regression: основным настраиваемым параметром выступал коэффициент L2-ре-гуляризации, варьируемый в логарифмически равномерной сетке значений. Это позволяло эффективно проводить переобучение при наличии мультиколлинеарности среди регрессоров.

• 4.    Random Forest Regressor: подбор включал следующие параметры: количество деревьев ( n_estimators ), максимальная глубина деревьев ( max_depth ), минимальное количество наблюдений в листе ( min_samples_leaf ), а также доля признаков, используемых при каждом разбиении ( max_features ). Данный подбор позволял адаптировать модель к различным структурам данных и уровню шумов.

• 5.    CatBoost Regressor: для данной модели использовалась обертка CatBoostRegressor совместно с GridSearchCV через scikit-learn API. Оптимизировались параметры: количество итераций ( iterations ), шаг обучения ( learning_rate ), глубина деревьев ( depth ), коэффициент L2-регуляризации ( l2_leaf_reg ) и минимальное число наблюдений в листе ( min_data_in_leaf ). Это обеспечивало устойчивость модели и высокую точность при наличии категориальных или разреженных признаков.

Каждая модель проходила отдельный цикл подбора гиперпараметров для каждого горизонта прогнозирования и уровня детализации структуры ИПЦ. Такой подход позволил учесть различия в статистических свойствах компонент индекса и обеспечить адаптивность моделей к конкретным условиям прогнозирования.

Результаты моделирования

В рамках эмпирического исследования протестированы три различных подхода к прогнозированию индекса потребительских цен, различа-

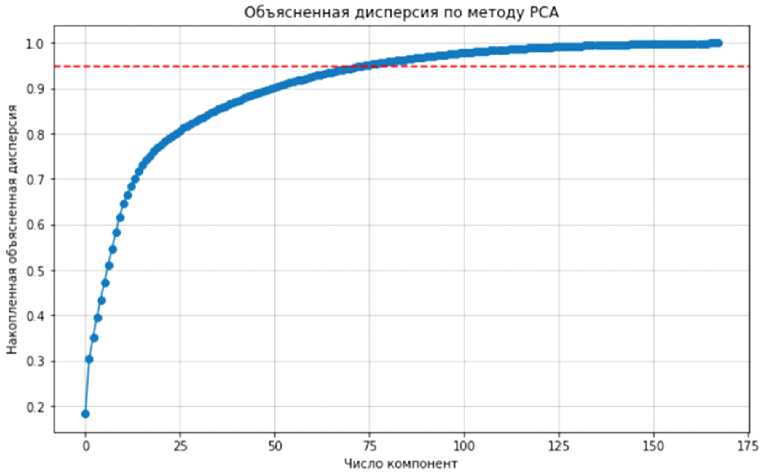
Рис. 1. Количество главных компонент PCA для сохранения 95 % дисперсии Примечание . Составлено авторами.

ющиеся уровнем агрегирования моделируемых компонент:

• 1)    агрегированный подход – прямое прогнозирование ИПЦ в целом, без предварительной декомпозиции на подгруппы;

• 2)    средний уровень агрегации – прогнозирование по трем укрупненным категориям: продовольственные товары, непродовольственные товары и услуги. Финальное значение ИПЦ восстанавливалось путем агрегирования соответствующих прогнозов с использованием официальных весов потребительской корзины по формуле (9):

ипц = 2X1 л* ^, (9)

где I_i – индекс потребительских цен на конкретный товар / услугу; w_i – вес конкретного товара / услуги в потребительской корзине; n – количество компонент ИПЦ;

• 3)    дезагрегированный подход – это индивидуальное моделирование 78 товарных и сервисных групп с последующим агрегированием аналогичным образом. Результаты расчетов представлены на рисунке 2.

В таблице 2 приведены данные об ошибке моделей на тестовой выборке.

Полученные результаты демонстрируют устойчивое преимущество покомпонентного модели- рования, при котором каждая товарная группа прогнозируется отдельно. Данный подход обеспечил наименьшее значение MAE на всех прогнозных горизонтах, особенно в кратко- и среднесрочной перспективе (до 9 месяцев). Отметим, что даже при более длительном горизонте (1–12 месяцев) точность данного метода остается сопоставимой с краткосрочными прогнозами по другим подходам.

Для формальной оценки значимости различий в точности моделей был применен тест Ди-болда – Мариано, основанный на сравнении среднеквадратичных ошибок (MSE) различных стратегий прогнозирования (см. табл. 3).

Таким образом, статистическая проверка подтверждает, что различия в точности прогнозов между подходами являются не случайными , а статистически значимыми. Особенно заметным является преимущество детализированного подхода над агрегированными.

Вклад в ошибку прогноза мы рассчитали по формуле (10):

Вклад = EX ^{i * ^wi , (10)

где I_i – отклонение фактического значения от прогнозного для отдельного товара / услуги; w_i – вес конкретного товара / услуги в потребительской корзине; n – количество компонент ИПЦ.

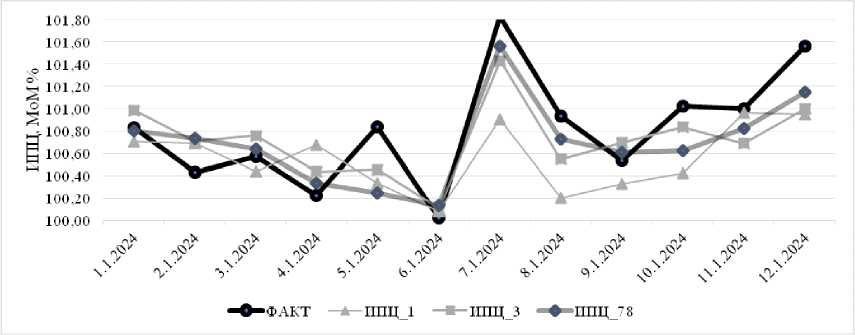
Рис. 2. Сравнительная оценка качества прогнозов ИПЦ в Ставропольском крае на основе агрегированного и дезагрегированного подходов

Примечание . Составлено авторами.

Таблица 2

Сравнение MAE различных подходов к моделированию ИПЦ

Подход	MAE
	1–3 мес.	1–6 мес.	1–9 мес.	1–12 мес.
ИПЦ в целом	0,17	0,26	0,38	0,39
ИПЦ по 3 компонентам	0,21	0,22	0,25	0,28
ИПЦ по 78 компонентам	0,13	0,20	0,20	0,23

Примечание. Составлено авторами.

Согласно проведенной декомпозиции прогностических ошибок (табл. 3), наибольший вклад в среднюю абсолютную ошибку вносили такие компоненты, как услуги пассажирского транспорта и мясопродукты. Это обусловлено, с одной стороны, их высокой волатильностью, с другой – существенной долей в структуре потребительской корзины, что усиливает их влияние на итоговое значение ИПЦ (рис. 3).

Дополнительно данные категории подвержены воздействию факторов, имеющих слабо предсказуемую природу. В частности, на динамику цен мясной продукции и плодоовощной группы значительное влияние оказывают эпизоотологические риски (например, вспышки заболеваний среди животных), а также погодные условия, критически важные для сельскохозяйственного производства.

Так, например, в мае – июне 2024 г. в Ставропольском крае наблюдалась аномально холодная погода, что привело к росту издержек производителей тепличных овощей на отопление. Это, в свою очередь, обусловило ускоренный рост цен на соответствующую продукцию по сравнению с предыдущими годами.

Заключение

В настоящем исследовании реализован многоуровневый подход к прогнозированию регионального индекса потребительских цен (ИПЦ) на примере Ставропольского края с использованием современных методов машинного обучения. Прогнозирование осуществлялось по трем уровням детализации: по агрегированному ИПЦ, по основным категориям (продовольственные и непродовольственные товары, услуги), а также по 78 товарным подгруппам. Такой подход позволил оценить влияние структуры и уровня детализации модели на точность прогнозов.

В качестве прогнозных алгоритмов использовались как классические статистические модели (SARIMA, Prophet), так и модели машинного обучения (Ridge Regression, Random Forest, CatBoost). Гиперпараметры подбирались с использованием GridSearchCV в сочетании с трех-фолдовой кросс-валидацией, основной метрикой выступила средняя абсолютная ошибка (MAE). Дополнительно применялись методы снижения размерности (PCA, где это применимо) и отбора

Таблица 3

Результаты теста Диболда – Мариано для оценки различий в точности прогнозов

Сравнение подходов	DM-статистика	P-value	Значимость (α = 0,05)
ИПЦ_1 vs ИПЦ_3	-2,347	0,0189	Различаются
ИПЦ_1 vs ИПЦ_78	-3,128	0,0018	Различаются
ИПЦ_3 vs ИПЦ_78	-1,892	0,0485	Различаются

Примечание. Составлено авторами.

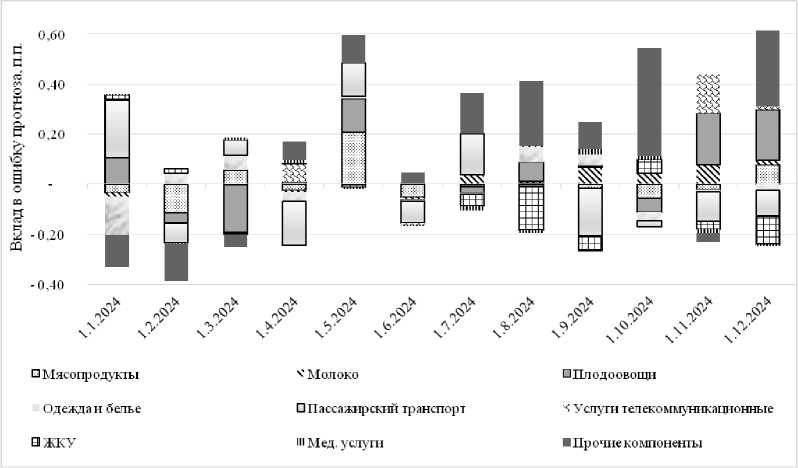
Рис. 3. Декомпозиция ошибки прогноза по вкладу отдельных компонент ИПЦ Примечание. Составлено авторами.

признаков (RFE, где это применимо), что позволило повысить интерпретируемость моделей.

Результаты эмпирического анализа показали, что на всех прогнозных горизонтах наиболее точные результаты демонстрирует подход, основанный на моделировании по отдельным товарным группам с последующим агрегированием. Подход, использующий три укрупненные категории, оказался менее точным, однако превзошел по качеству прогнозы, полученные при моделировании общего ИПЦ без дезагрегации.

Дополнительный анализ ошибок показал, что наибольший вклад в отклонение прогнозов вносили компоненты с высокой волатильностью и значительным весом в структуре потребительской корзины, что подчеркивает важность учета специфики отдельных товарных групп и использования гибких моделей, способных адаптироваться к различным источникам неопределенности, включая внешние шоки и погодные аномалии.

Полученные выводы подтверждают репрезентативность покомпонентного подхода к прогнозированию инфляции и обосновывают важность его применения в региональной практике, особенно в условиях ограниченности данных и повышенной волатильности отдельных рынков.