DFT моделирование взаимодействия водорода с вакансией в ОЦК-железе

Известно, что водород оказывает значительное влияние на физические и механические свойства железа и сплавов на его основе [1–3]. Современное понимание механизма водородного охрупчивания предполагает, что водород из окружающей среды растворяется в стали, мигрирует к центрам внутреннего напряжения, таким как вершины трещин, где он накапливается, и, в конечном счете, способствует зарождению и распространению трещин, разрушающих материал [4]. Важную роль в этом процессе играет захват водорода дефектами решетки, такими как примесные атомы, дислокации, границы зерен, межфазные границы [5–7]. Поскольку примеси внедрения, к числу которых относится водород, обладают низкой растворимостью и высокой мобильностью в железе и в сталях, экспериментальные исследования микроскопических механизмов взаимодействия водорода с дефектами в металлах являются достаточно трудоемкими. В условиях устойчивого роста вычислительной мощности и прогресса в развитии эффективных алгоритмов, моделирование на атомном уровне является альтернативным способом проведения исследований указанных процессов. В работах [8, 9], было проведено исследование взаимодействия атомов водорода с примесными атомами замещения при помощи первопринципных расчетов. Данная работа посвящена взаимодействию водорода с другим видом точечных дефектов – вакансиями. Связано это, прежде всего с тем, что в ряде исследований отмечено существование притяжения между вакансиями и атомами водорода в α-железе [9–12]. Оказалось, что в одной вакансии могут накапливаться до шести атомов водорода [7, 13]. Подобное взаимодействие приводит к росту концентрации вакансий, о чем свидетельствует ряд экспериментов [14, 15].

Несколько вычислительных работ было посвящено исследованию поведения водорода в железе, включая энергию его растворения, предпочтительное расположение, диффузионный барьер, энергию связи водорода с моновакансиями, дислокациями и примесными атомами [16–23]. В работах [24–26] было также показано, что изменения, связанные с примесями в электронных и магнитных свойствах могут быть также важны. Однако есть еще несколько открытых вопросов, в частности тех, которые касаются взаимодействия между водородом и вакансиями в разных магнитных состояниях. В этой работе мы впервые провели расчет взаимодействия водорода с вакансией в парамагнитном состоянии, и сравнили его с результатом для ферромагнитного ОЦК железа [27].

Методы

Первопринципные расчёты были выполнены в рамках теории функционала плотности (DFT) методом линейных присоединенных плоских волн (LAPW) с учётом обобщённого градиентного приближения (GGA’96) в программном пакете WIEN2k. Это наиболее точные методы, используемые в рамках теории функционала плотности (DFT). Для расчётов использовался мощный вычислительный комплекс Торнадо [28]. При интегрировании в обратном пространстве и вычисления электронной плотности использовалась схема Монхорста-Пака с сеткой 3 х 3 х 3 к -точек зоны Бриллюэна. Расчёты проводились при значениях параметров моделирования: параметр сходимости Kmax = 5 a.е.^–1, радиусы MT-сфер Rmt(Fe) = 2,00 a.е. [29], Rmt(H) = 0,70 a.е [20]. Эти параметры обеспечивают погрешность результатов расчётов не более 0,01 эВ.

ОЦК-решетка железа устойчива при температурах ниже 1184 K причем в области ниже точки Кюри (1043 K) система ферромагнитна, а в диапазоне температур 1043–1183 K – парамагнитна. Особенности программного пакета WIEN2k позволяют провести моделирование только основного состояния системы при 0 К. Поэтому при моделировании ОЦК-железа в ферромагнитном состоянии параметр решетки определялся минимизацией полной энергии системы и был равен a = 2,84 Å [29]. Поскольку нас интересует влияние магнитного состояния на взаимодействия водорода с вакансией, то крайне важно использовать реалистичную плотность электронного газа характерного для парамагнитного состояния. По этой причине мы использовали не равновесный параметр решетки при 0 К, а параметр полученный из эксперимента при соответствующей температуре парамагнитного состояния [30]: a = 2,90 Å (для 1110 К). Суперячейка состоит из 54 атомов железа. Оптимизация геометрии выполняется до тех пор, пока сила, действующая на каждый атом, не станет меньше 0,0257 эВ/ Å (0.001 Рб/Бор).

Расчёт энергии образования вакансии для суперячейки, состоящей из N атомов железа и одной вакансии, производился по следующей формуле:

Ef (—) = E(—-1,1,Q)-—E(—,0,Q), где E(—, m, Q) - энергия структуры, содержащей — атомов и m вакансий в равновесном объёме Q.

Энергия захвата атома водорода в одиночную вакансию, содержащую n – 1 атомов водорода, с образованием комплекса V H _n , определялась соотношением:

Etap (1,n) = E(1,n-1,Q)+E(0J,Q)-E(0,0,Q)-E(1,n,Q), где E(1, n, Ω) – энергия системы, состоящей из 53 атомов железа и n атомов водорода, находящихся внутри вакансии в равновесном положении с объемом Q; E(0,1,Q) - энергия системы из 54 атомов железа и атома водорода в тетрапоре; E(0,0,Ω) – энергия системы из 54 атомов чистого железа при равновесном объёме Q.

Результаты и обсуждение

Ферромагнитное состояние ОЦК-железа

Было рассчитано значение энергии образования вакансии, равное E _v ^f _ac( N ) = 2,15 эВ для ферромагнитного состояния, что находится в хорошем согласии как с экспериментальными данными 1,6÷2,2 эВ [31], так и с результатами других вычислительных работ. В работе [32] с использованием программного пакета VASP в таком же приближении было получено аналогичное значение E _v ^f _ac( N ) = 2,15 эВ, а в работе [23] с использованием того же программного продукта энергия образования вакансии E _v ^f _ac( N ) = 2,17 эВ.

На следующем этапе было вычислена энергия связи комплекса водород–вакансия. Для этого необходимо было определить равновесное положение атома водорода в ячейке с вакансией. В первую очередь водород был помещен в вакансию, так как, на первый взгляд, это положения кажется наиболее предпочтительным ввиду высокой симметрии данной конфигурации. Однако значение энергии образования вакансии в такой системе E _v ^f _ac ( N ) = 2,70 эВ, что существенно выше энергии образования вакансии для чистого железа, а энергия связи водорода с вакансией E _trap (1,1) = –0,22 эВ, что может свидетельствовать о том, что вакансия пытается вытолкнуть водород.

Физика

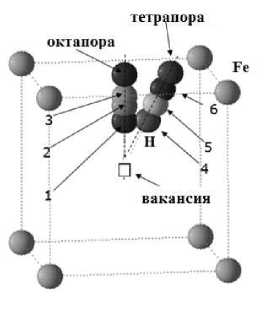
Рис. 1. Схематическое представление положения атома водорода (1,2,3,4,5,6) в ячейки с вакансией ОЦК-железа

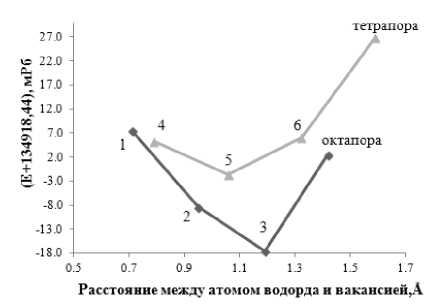
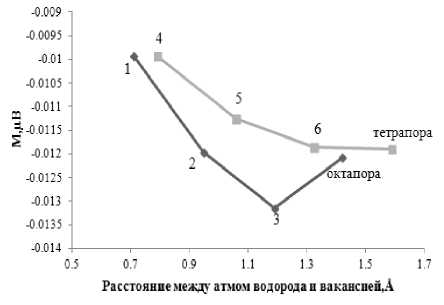
а)                                                           б)

Рис. 2. Зависимость энергии системы (а) и магнитного момента (б) от расстояния между атомом водорода и вакансией

С целью нахождения оптимального положения водорода были выбраны точки вдоль двух прямых, одна из которых соединяет вакансию с октапорой, а другая – с тетрапорой (рис. 1). На рис. 2, а представлен график зависимости энергии системы от расстояния между атомом водорода и вакансией. Таким образом, было показано, что водород смещается на 0,23 Å от октапоры в направлении вакансии. Данному положению водорода соответствует минимум зависимости магнитного момента (рис. 2, б ). Отметим, что направление магнитного момента на атоме водорода антипараллельно магнитному моменту на атомах Fe. Возможно, что положение равновесия для атома водорода определяется именно магнитным взаимодействием с окружающей матрицей. Данной конфигурации соответствует энергия связи E _trap (1,1) = 0,60 эВ.

В экспериментах по захвату дейтерия в ОЦК-железе было показано, что водород располагается на расстоянии 0,4±0,1 Å от октапоры, что соответствует E _trap (1,1) = 0,63 эВ [33]. В работе [16], в которой также использовался метод DFT, расстояние между водородом и октапорой составляет 0,22 Å и E _trap (1,1) = 0,55 эВ. В работе [23] водород находится на расстоянии 0,20 Å от октапоры и E _trap (1,1) = 0,57 эВ. Таким образом, полученные результаты хорошо согласуются как с экспериментом, так и с данными расчетов других авторов.

Парамагнитное состояние ОЦК-железа

Одна из основных проблем моделирования парамагнитного состояния заключается в том, что в реальном парамагнитном ОЦК-железе магнитные моменты атомов разупорядочены. При моделировании неупорядоченных бинарных сплавов важно добиться, чтобы конфигурации в рассматриваемой суперячейке не были близки к какой-либо упорядоченной структуре. Дело в том, что сплавы с неупорядоченной и упорядоченной структурой имеют существенно разную энергию, и это может исказить результат моделирования. Для получения такого неупорядоченного распределения использовался программный пакет BINAR [34]. Программа перебирает все возможные

Верховых А.В., DFT моделирование взаимодействия водорода Мирзоев А.А. с вакансией в ОЦК-железе способы расположения атомов с различными направлениями спина в суперячейке, разбивая анализируемые конфигурации на группы. При этом в одну группу включаются все конфигурации, которые могут быть получены друг из друга при помощи операций симметрии разрешенных для данной кристаллической решетки. Полученные таким образом конфигурации, относящиеся к разным группам, проверяются на соответствие критерию «неупорядоченности», и в случае несоответствия отбраковываются. В программе в качестве критерия используется гистограмма статистического распределение атомов во втором окружении для биномиального распределения (абсолютно неупорядоченный сплав). В данной работе, с помощью программы BINAR были получены 15 различных неэквивалентных магнитных конфигураций. Для дальнейшего анализа были выбраны 5 конфигураций, лежащие ниже остальных по энергии.

По известной разности энергии n -конфигурации системы и энергии системы в основном состоянии, была вычислена каноническая статистическая сумма (S):

S = n=1 Sn, Sn = exp (-) , где E0 – энергия основного состояния, а En – энергия системы в n-ом энергетическом состоянии; k-коэффициент Больцмана, Т = 1110 К (средняя температура существования ОЦК-фазы железа в парамагнитном состоянии).

Из отношения вклада в статсумму от данной конфигурации ко всей статсумме была вычис лена вероятность существования магнитного состояния и , соответственно , степень влияния дан ного состояния на энергию формирования вакансии ОЦК - железа и энергию захвата атома водо рода вакансией :

P = S n n S

В табл . 1 представлены : разница в энергии E_n–E₀, вероятность P_n и соответствующие энергии формирования вакансии . Видно , что парамагнитное состояние снижает энергию формирования вакансии на 0,37 эВ (17 %), что хорошо согласуется с экспериментальными данными . Это гово рит о работоспособности выбранного нами метода и возможности моделирования им других энергетических характеристик , таких как энергия захвата атома водорода вакансией .

Таблица 1

Энергии и вероятности существования 5 парамагнитных конфигураций ОЦК-железа и соответствующие энергии формирования вакансии.

Номер конфигу рации n	E n – E 0 , эВ	Вероятность P n , %	Энергия формирования вакансии , эВ
1	0,69	0,06	1,96
2	0	79,69	1,67
3	0,14	17,42	2,12
4	0,70	0,05	1,93
5	0,31	2,90	2,49
Среднее	—	—	1,78
Эксперимент : [35] [36] [37] [38] [39]	—	—	1,5±0,1 1,53±0,15 1,40±0,10 1,60±0,10 1,79±0,10
Ферромагнитное состояние	—	—	2,15

Физика

Таблица 2

Расстояние между атомом водорода и соответствующей октапорой и энергия захвата для различных пространственных конфигураций спинов в парамагнитном ОЦК железе

Номер конфигурации n	Вероятность P n , %	Расстояние H–октапора, Å	Энергия захвата атома водорода вакансией, эВ
1	0,06	0,18	0,39
2	79,69	0,24	0,26
3	17,42	0,19	0,30
4	0,05	0,17	0,44
5	2,90	0,24	0,42
Среднее	—	0,23	0,27
Ферромагнитное состояние	—	0,23	0,60

В парамагнитном состоянии ОЦК-железа водород был помещен в 5 различных конфигураций на расстоянии 0,23 Å от октапоры, а затем была выполнена релаксация структур для нахождения оптимального положения атомов систем. В табл. 2 представлены значения энергии захвата атома водорода вакансией, расстояния между атомом водорода и октапорой, а также соответствующие вероятности существования различных магнитных структур. Данные результаты показывают, что энергия захвата атома водорода вакансией понижается почти в 2 раза, а расстояние между атомом водорода и центром октапоры остается таким же, как и в случае ферромагнитного состояния. Однако, из-за того, что в парамагнитном состоянии параметр решетки равен 2,90 Å, что на 2 % больше, чем в случае ферромагнитного состояния, расстояние между центром вакансии и октапорой увеличивается, следовательно, и расстояние между водородом и центром вакансии увеличивается. Поскольку во всех парамагнитных конфигурациях параметр решетки один и тот же, то различия энергий наблюдаемых в табл. 2 не может быть связано с геометрическим фактором, таким образом, мы приходим к выводу, что изменения энергии в различных конфигурациях может быть связано только с флуктуациями магнитного порядка. Таким образом, следует признать, что локальный магнитный порядок значительно влияет на растворение водорода.

Заключение

В работе проведено DFT компьютерное моделирование энергии взаимодействия водорода с вакансией в ОЦК железе. С использованием пакета BINAR получены значения энергии образования вакансии и энергия захвата атома водорода одиночной вакансией в парамагнитном состоянии в ОЦК железе. Среднее значение энергии формирования вакансии 1,78 эВ, хорошо согласуется с существующими экспериментальными данными. Обнаруженная зависимость энергии захвата водорода вакансией в парамагнитном случае от ближнего магнитного порядка свидетельствует о магнитной природе снижения данной величины по сравнению с ферромагнитным ОЦК-железом при 0 К.