DFT Simulations of g-C2O Monolayer as Energy Storage Material

The C2O monolayer is a material with a high specific surface area and, consequently, a potentially large number of adsorption sites for lithium ions and molecular hydrogen. This feature makes it a promising candidate for applications in lithium-ion batteries and hydrogen storage devices. The stability of this material has been previously predicted by theoretical methods [1], and its properties as a hydrogen separation membrane have been investigated [2]. In this study, we used density functional theory (DFT) to research the mechanisms of hydrogen and lithium sorption at the atomic level and to estimate the energy characteristics of the adsorbate-surface interactions.

DFT calculations can be computationally demanding, especially when accurate dispersion corrections are required for simulating weakly interacting systems. Furthermore, the presence of a high vacuum volume in the model necessitates a careful choice of methodology. Therefore, the use of localized pseudo-atomic orbitals as a basis set for wavefunction decomposition represents a reasonable approach. This type of basis set can yield accurate and efficient results provided that thorough corrections for the basis set superposition error (BSSE) are applied [3, 4]. We have previously demonstrated that after applying energy and geometry corrections for BSSE, results obtained with such a basis set can be as accurate as those from plane-wave basis set calculations, which are inherently free from the BSSE [5]. In this paper, we successfully simulated the atomic structure and sorption properties of the g-C 2 O monolayer using computational resources limited to those of a personal computer.

Models and simulation details

Numerical experiments were performed with periodic boundary conditions using the SIESTA software package [6], which employs an atomic-orbital basis set for wavefunction decomposition. We treated the 2s²2p² electrons for C, 2s²2p⁴ electrons for O, 2s¹ electron for Li, and 1s¹ electron for H as valence electrons. Norm-conserving pseudopotentials were taken from the database for the PSF format [7]. We utilized a double-ζ polarized basis set (DZP [8]), where three finite functions are used for each atomic orbital: the main, modified, and polarized orbitals. To account for van der Waals interactions, we employed the semi-empirical dispersion correction scheme by Grimme (DFT-D2) [9] in conjunction with the Perdew–Burke–Ernzerhof (PBE) exchange-correlation (XC) functional [10], as well as the vdW-DF functional of Dion et al. [11] with exchange modified by Berland and Hyldgaard (vdW-DF2-

BH) [12]. Test spin-polarized calculations of the pristine, Li-decorated, and H 2 -adsorbed g-C 2 O monolayer showed that all investigated systems were non-magnetic. Therefore, to accelerate the calculations, most production simulations were performed without spin polarization. The simulation parameters used in this work, which allowed us to achieve a precision in binding energy calculations of approximately 5 meV, are summarized in Table 1.

Table 1

Simulation parameters

XC functional	PBE+D2	BH-vdW
k -points	5×5×1
MeshCutoff, Ry	450 (≈6,12 keV)
Total energy convergence criterion, eV	10–6
Force convergence criterion, Ry/Bohr	5·10–5 (≈1,3 meV/Å)
Vacuum layer, Å	33 Å
Optimized translational parameter, Å	8,26	8,25

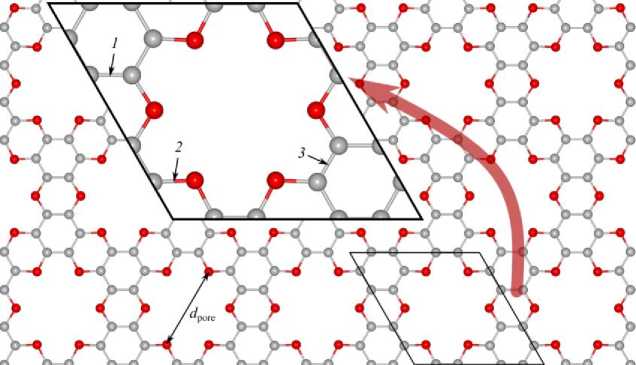
The hexagonal simulation cell contained 12 carbon and 6 oxygen atoms. Fig. 1 shows the atomic structure of the g-C 2 O monolayer after geometry relaxation. The equilibrium lattice parameter was determined by minimizing the total energy of the system. Both employed exchange-correlation functionals yielded similar structural parameters. The calculated bond lengths and pore diameter ( d pore = 5,37 A and 5,35 Å for PBE+D2 and BH-vdW functionals, respectively) are in good agreement with previous studies of the g-C 2 O monolayer [1, 2].

Я”Я о—ц 00 0—0 p—о

Vo o-4  4-0  o-4  4-0  0-4 VV i ^-4 Vo oV b-«        0—0'       VV       Ve        0-0

Fig. 1. Top view of the optimized atomic structure of the C 2 O monolayer obtained using the PBE+D2 functional. Carbon and oxygen atoms are represented by grey and red spheres, respectively. The unit cell boundary is indicated by a solid black line. The lattice parameters l for the different XC approximations are listed in Table 1. The calculated bond lengths are (1) 1,41, (2) 1,39, and (3) 1,40 Å. All structural images were generated using the VESTA 3 software package

The binding energies of a Li atom and a hydrogen molecule were calculated using the following equation:

E bind = E ad + E C 2 O - E C 2 O + ad - I E CP I,                            (1)

where E_ad , E _CO, and E _{C O +ad} are the total energy of an isolated adsorbate (a Li atom or a hydrogen molecule), an isolated C₂O monolayer, and the adsorbate-substrate system (decorated g-C₂O monolayer), respectively; E is the Boys–Bernardi counterpoise correction for the basis set superposition error [13]. Note, that with this definition, a positive value of the binding energy corresponds to an attractive interaction between the adsorbate and the C₂O monolayer.

Pseudo-atomic basis set optimization

Since all calculations were performed using a localized atomic-orbital basis set, the basis set parameters were optimized prior to the sorption simulations to ensure the highest possible accuracy of the binding energy estimates. We monitored the convergence of the total energy of the g-C2O monolayer

Физика and “pressure” P for geometrical parameter with respect to the basis set cutoff radius, following the procedure detailed in [5]. The resulting convergence dependencies are presented in fig. 2.

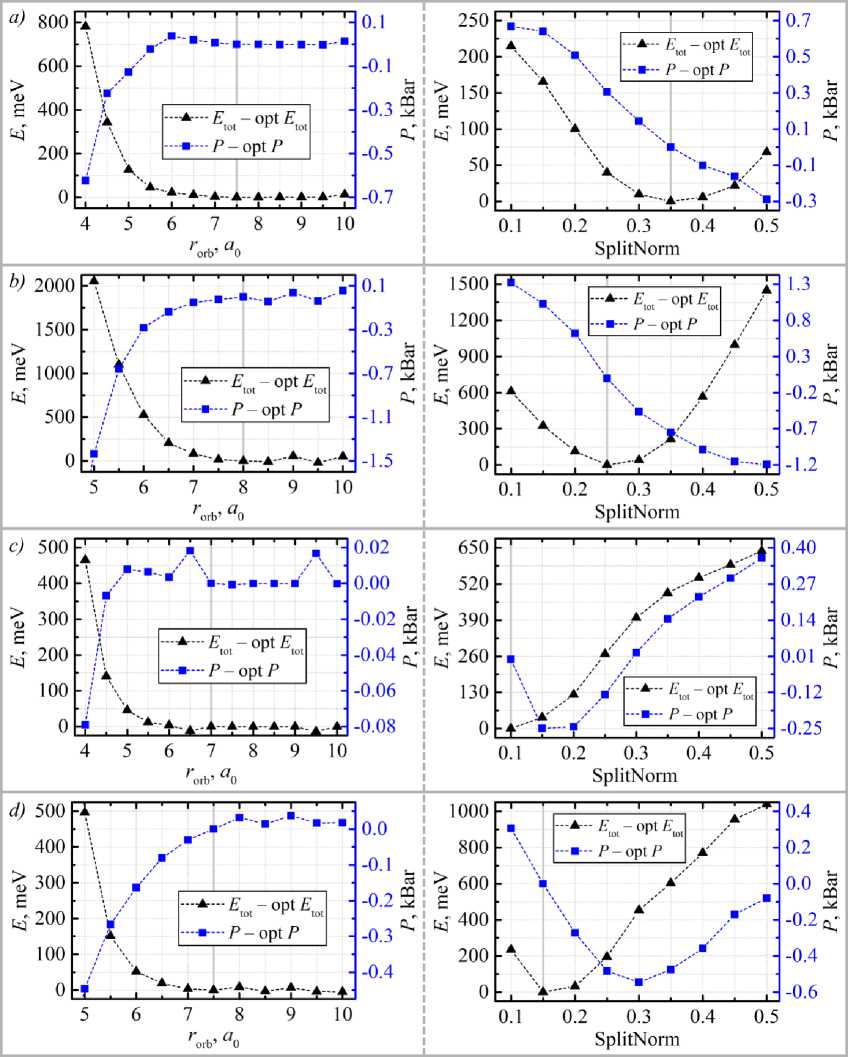
Fig. 2. Convergence of the total energy and the parameter P of the C 2 O monolayer with respect to the cutoff radii of a ) C(2s), b ) C(2p), c ) O(2s), and d ) O(2p) atomic orbitals. The left panels show the dependencies for the first-ζ (main) orbital function, while the right panels correspond to the second-ζ (modified) orbital function (the cutoff radius for the latter is controlled by the SplitNorm parameter [8]). The chosen as optimal values are marked by solid gray vertical lines. The atomic orbital radii are given in Bohr radius ( a ≈ 0,53 Å).

As shown in fig. 2, the convergence behavior for all considered valence orbitals was consistent with theoretical expectations. Consequently, the optimal basis set parameters were selected according to standard criteria: the cutoff radius for the first-ζ (main) orbital function was chosen at the point where both the total energy and the parameter P reached stable plateau values, while the SplitNorm parameter for the second-ζ (modified) function was optimized to minimize the total energy of the g-C 2 O monolayer. The specific basis set parameters selected for all subsequent simulations are summarized in table 2.

The default basis set parameters are indicated in parentheses in table 2 for com- Basis set parameters Table 2 parison. It is evident that these default parameters differ significantly from the optimized values obtained in this work. Fur- Orbital r , a0 rm , a0 SplitNorm C(2s) 7,64 (4,09) 2,81 (3,35) 0,35 (0,15) thermore, we have previously demonstrated C(2p) 8,03 (4,87) 3,22 (3,48) 0,25 (0,15) that the default cutoff radii are insufficient for accurate simulations of H2 sorption [5]. Therefore, the optimized basis set parame- O(2s) 7,00 (3,31) 2,77 (2,51) 0,10 (0,15) O(2p) 7,54 (3,94) 2,74 (2,54) 0,15 (0,15) ters presented here are recommended for future simulations of decorated and/or defective g-C2O monolayer. For hydrogen and lithium the following parameters were used: r= 6, 05a0 and rm = 2,52a0 for

H(1s) orbital; r = 7, 78 a ₀ and r_m = 7, 68 a ₀ for Li(2s) orbital.

Hydrogen sorption on the g-C2O monolayer

The initial position of the H2 molecule was above the center of an oxygen pore, as this configuration was previously identified as the most energetically favorable in a similar material [14]. After geometry relaxation, the H2 molecule remained centered above the pore with its molecular axis perpendicular to C2O sheet (fig. 3, b). The binding energy was calculated using eq. (1) for the different dispersion corrections. Furthermore, to account for the BSSE in the relaxed geometry [5, 14], we calculated the BSSE-corrected H2-monolayer distance ( d ) and the corresponding corrected binding energy. All binding energy results are summarized in fig. 3a. The calculated distances for the PBE+D2 approximation were d = 1,71 Å and dcorr = 1,96 Å. For the BH-vdW functional, the distances were d = 2,23 Å and dcorr = 2, 41 Å. A significant discrepancy between the two functionals is evident: the BH-vdW estimations for the H2-monolayer distance are more than 20 % larger than those obtained with the PBE+D2 functional. Moreover, the PBE+D2 results were more sensitive to the BSSE geometry correction, with d being 15 % larger than uncorrected distance d . For the BH-vdW functional, this increase was less than 10 %.

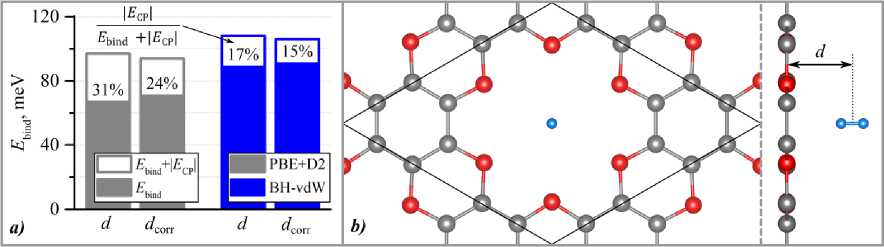
Fig. 3. Hydrogen sorption on the C 2 O monolayer: a ) binding energy of an H 2 molecule calculated using different dispersion corrections, with and without BSSE corrections applied to the system geometry; b ) top and side view of H 2 adsorbed above the oxygen pore. The structure shown is the optimized geometry obtained using the BH-vdW functional, prior to the application of the BSSE correction.

Fig. 3, a shows that for all used functionals the counterpoise (CP) correction for the BSSE accounted for a considerable fraction (up to 30 %) of the uncorrected binding energy. While the geometry optimization with the BSSE correction slightly improved the situation, the subsequent CP corrections remained significant. This indicates that for weakly bonded systems, an energy correction for the BSSE is essential. Surprisingly, the hydrogen binding energies obtained with the PBE+D2 functional were approximately 20 % lower than those from the BH-vdW functional, despite the considerably shorter H₂-monolayer distances observed with the Grimme correction scheme. Overall, the binding energy did not exceed 100 meV per H 2 molecule, which is far too low for the desired roomtemperature application of the C₂O monolayer as a hydrogen storage material.

Lithium sorption on the g-C2O monolayer

We also simulated the sorption of a single lithium atom on the g-C 2 O monolayer to evaluate the nature of its bonding. The initial position for the Li atom was chosen above the center of the oxygen pore,

Физика as this site was previously reported to be the most energetically favorable in a similar material [15]. After geometry relaxation, the g-C2O layer exhibited a sight distortion (see fig. 4, b, Al = 0,65 A and 0,62 Å for the BH-vdW and the PBE+D2 functionals, respectively). The Li atom remained coordinated to the oxygen pore but was displaced from its center. The lithium binding energy was calculated using Eq. (1). In this case, geometry correction for the BSSE was deemed unnecessary, as increasing the Li-C2O distance did not lead to a more favorable total energy. The resulting Li binding energies are presented in fig. 4, a.

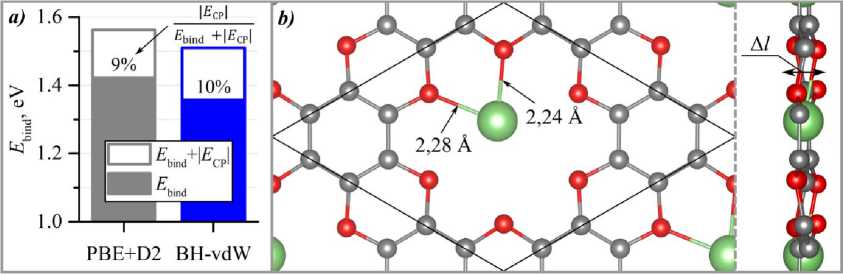
Fig. 4. Lithium adsorption on the C 2 O monolayer: a ) binding energy of a Li atom calculated using different dispersion corrections; b ) top and side view of the optimized structure of a Li atom adsorbed at the oxygen pore site, obtained using the BH-vdW functional

Fig. 4, a shows that in the case of Li adsorption, the energy correction for the BSSE plays a less significant role than for H 2 adsorption: the CP correction does not exceed 10 % of the uncorrected Li binding energy. Furthermore, the different dispersion corrections yielded consistent results for lithium, with only a ~5 % difference between the estimates obtained with the PBE+D2 and BH-vdW functionals. Overall, the Li atom binds to the C 2 O monolayer with an energy of approximately 1,4 eV. While this value is adequate for lithium-ion battery applications, it is lower than the cohesive energy of bulk lithium (~1,6 eV). This makes lithium an ineffective decorative agent for enhancing hydrogen sorption, as Li atoms will tend to cluster with increasing concentration. The inner atoms in such clusters would not participate in hydrogen binding.

Conclusion

The pristine and Li-/H 2 -decorated g-C 2 O monolayer was investigated using density functional theory with a pseudo-atomic orbital basis set for wavefunction decomposition. The relaxed C₂O atomic structure was obtained for the considered functionals, and the optimized parameters for the atomic orbital basis functions were determined. These parameters can be utilized in future simulations of C 2 O-based systems.

For hydrogen molecule adsorption, the center of the H2 molecule was located at a distance of 2,02,4 Å from the monolayer (depending on the dispersion corrections scheme). The calculated binding energy ranged from 70 to 90 meV, which is below the optimal range of 200–600 meV required for effective sorption-desorption cycles under practical conditions. This indicates that the hydrogen molecule interacts too weakly with the C2O surface to be retained effectively, diminishing the prospects of using the pristine monolayer in hydrogen storage applications without further surface modification.

The lithium binding energy was approximately 1,4 eV, with the atom occupying the oxygen pore site of the slightly distorted monolayer. While this value falls within the acceptable range for lithium-ion battery anods, further simulations with higher lithium concentrations are necessary to draw definitive conclusions regarding the application of C 2 O in lithium batteries. Importantly, the lithium binding energy is lower than the cohesive energy of bulk lithium (~1,6 eV). This implies that decorating the C₂O monolayer with lithium is not a viable strategy for enhancing hydrogen binding energy, as potential clustering of lithium atoms would reduce the overall hydrogen capacity of the material.

The study was supported by a grant from the Russian Science Foundation No. 25-22-20023,