Диагностирование относительной жесткости упругих краевых ребер цилиндрической оболочки

Электронный журнал «Техническая акустика»

Круговые цилиндрические оболочки являются элементами сложных механических систем, широко используемых в технике. Известно, что величины жесткости закреплений краевых ребер оболочек со временем могут менять свои значения в связи с усталостью материалов и температурными изменениями. Поэтому, определение жесткостей закреплений краев оболочек важно для проверки надежности работы механической системы. Об относительной жёсткости упругих краевых ребер цилиндрической оболочки чаще можно судить после разборки механической системы. Поэтому в настоящее время развивается направление, возникшее на стыке теории механизмов с акустикой [1, 2], решающее задачи оперативного контроля технических конструкций без их разборки.

Целью настоящей работы является определение жесткости упругих закреплений цилиндрических оболочек по собственным частотам их колебаний. Ранее подобная задача для оболочек не решалась. Возможности акустического диагностирования рассматривались для струн, мембран, стержней и пластин [3 – 7].

Математическое содержание проблем колебаний оболочек сводится к рассмотрению линейных, однородных дифференциальных уравнений с однородными краевыми условиями. Коэффициенты дифференциальных уравнений являются функциями, содержащими в себе частоту свободных колебаний. Влияние ряда краевых условий на величины собственных значений задач колебаний оболочек исследовалось в работах [8 – 15]. Однако, обратная зависимость — зависимость краевых условий от собственных частот — в этих работах не рассматривалась.

1. ПРЯМАЯ ЗАДАЧА

Прежде чем поставить обратную задачу — задачу диагностирования — рассмотрим влияние упругости закрепления краевых ребер на собственные значения замкнутых круговых ортотропных цилиндрических оболочек. Задача об осесимметричных колебаниях оболочек с упругими краевыми рёбрами сводится [10] к спектральной задаче y 4( x) - Л4 y (x) = 0                                                                        (1)

с краевыми условиями:

y "(0) = y "( l ) = 0;

y "'(0) + B о l -3 y (0) = 0;                                                                            (2)

y ^w( l ) - Bl - y ( l ) = 0.

Здесь 2 — собственное значение задачи, которое связано с частотным параметром ш [10], B — относительная жёсткость рёбер; причем в сечении x = 0 цилиндрической оболочки имеем B ₀ , в сечении x = l — B_l .

Так как Л⁴ > 0, то при двух мнимых и двух действительных корнях характеристического уравнения общее решение уравнения (1) можно представить в виде

y ( x ) = C 1 cosh Л х + C ₂ cos Л х + C 3 sinh Л х + C ₄ sin Л х .

Стандартными методами с помощью характеристического детерминанта [15] находится трансцендентное уравнение для краевой задачи (1):

a ⁶(1 - cosh a cos a ) + a ³( B ₀ + B l )(sinh a cos a - cosh a sin a ) + 2 B ₀ B l sinh a sin a = 0.   (3)

Здесь a = Л1  — безразмерный параметр, зависящий от вида решения дифференциального уравнения и краевых условий. Из уравнения (3) при различных значениях относительной жесткости определяются собственные значения замкнутых круговых цилиндрических оболочек. Такое влияние краевых условий на величины собственных значений хорошо изучено [10]. Мы рассмотрим обратное влияние — влияние собственных частот на краевые условия.

соответствующий общему случаю, когда 0 <  B_0l < к (т. е. допускается и случай абсолютно жесткого закрепления).

Поскольку учитывается жесткое закрепление, то краевые условия (2) задачи (1) правильнее записать в виде:

У "(0) = y "( l ) = 0;

a i у "'⁽⁰) + a о у ⁽⁰⁾ = ⁰;                                                                             (4)

b i у '"( i ) - ь 0 у ( i ) = 0.

Здесь B ₀ l ^{- 3} = a ₀ a ₁ ^{- 1}; B_ll ^{- 3} = b ₀ b ₁ ^{- 1}.                                                          (5)

При абсолютно жестком закреплении ребер в краевых условиях (2) остаются только вторые слагаемые. Этому же соответствует случай a ₁=0, b ₁=0 в краевых условиях (4).

Обозначим матрицу, составленную из коэффициентов краевых условий (4), через А :

aa 00

A = ^{0 1}             ,

• 1 0 0 - ь 0 b i )’

• 3. МЕТОД РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ

а миноры, составленные из i -го и j -го столбцов этой матрицы — через M_ij ( i = 1, 2, 3; j = 2, 3, 4.).

В таких обозначениях задача диагностирования формулируется следующим образом. Известны отличные от нуля собственные значения A i задачи (1), ранг матрицы A равен 2, миноры M ₁₂ и M ₃₄ этой матрицы равны нулю; неизвестны коэффициенты a ₀, a ₁, b ₀, b ₁ краевых условий (4). Требуется восстановить матрицу A с точностью до линейной эквивалентности.

Частотное уравнение для краевой задачи (1) находим стандартными методами [15]. Приравнивая к нулю характеристический детерминант Д _A , получим

M 13 f , ( A i ) + ( M 14 - M 23 ) f 2 ( A , ) + M 24 f 3 ( A i ) = 0; i = 1,2,                                 (6)

где f 1 ( A ) = 2sinh A l sin A l , f 2 ( A ) = A ³(cosh A l sin A l - sinh A l cos A l ), f . ( A) = A ⁶(cosh A l cos A l - 1).

Пусть A1 и A2 — два собственных значения спектральной задачи (1), (4), соответствующие первым двум частотам осесимметричных колебаний оболочки. Тогда равенства (6) представляют собой систему двух уравнений от трех неизвестных M13 , (M14 - M23 ), M24 . Если ранг системы уравнений (6) равен двум, то система имеет единственное решение с точностью до постоянного множителя. Определив все неизвестные миноры M ij , можно найти матрицу A с точностью до линейных эквивалентных матриц, т. е. восстановить краевые условия задачи (1).

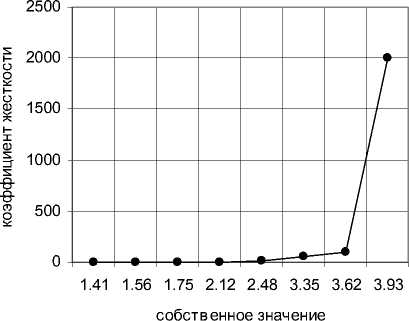
В приведенных ниже таблице и диаграммах представлены изменения значений жесткости закрепления на одном из краевых ребер оболочки в зависимости от изменений собственных значений спектральной задачи (1), (4). В них можно увидеть зависимость коэффициента относительной жесткости B_l (при фиксированном B ₀ ) от собственных значений λ ₁ и λ ₂ данной спектральной задачи.

Таблица 1. Зависимость коэффициентов относительной жесткости от собственных значений задачи (1), (4)

№	B 0	B l	Вид частотного уравнения (6)	Корни уравнения (6): λ 1 ; λ 2
1	1	0	f 2 ( λ i ) + f 3 ( λ i ) = 0	1,410843600; 4,739520795
2	1	1	f 1 ( λ i ) - 2 f 2 ( λ i ) - f 3 ( λ i ) = 0	1,564153306; 4,748887841
3	1	2	2 f 1 ( λ i ) - 3 f 2 ( λ i ) - 2 f 3 ( λ i ) = 0	1,750140001; 4,758314548
4	1	5	5 f 1 ( λ i ) - 6 f 2 ( λ i ) - 5 f 3 ( λ i ) = 0	2,124978866; 4,786924343
5	1	10	10 f 1 ( λ i ) - 11 f 2 ( λ 1 ) - 10 f 3 ( λ i ) = 0	2,477953280; 4,835531486
6	1	50	50 f 1 ( λ i ) - 51 f 2 ( λ i ) - 50 f 3 ( λ i ) = 0	2,477953280; 4,835531486
7	1	100	100 f 1 ( λ i ) - 101 f 2 ( λ i ) - 100 f 3 ( λ i ) = 0	3,622201070; 5,632310215
8	1	2000	2000 f 1( λ i ) - 2001 f 2( λ i ) - 2000 f 2( λ i ) = 0	3,927120456; 6,979162672
9	1	∞	f 1 ( λ i ) - f 2 ( λ i ) = 0	3,943181652; 7,071418764

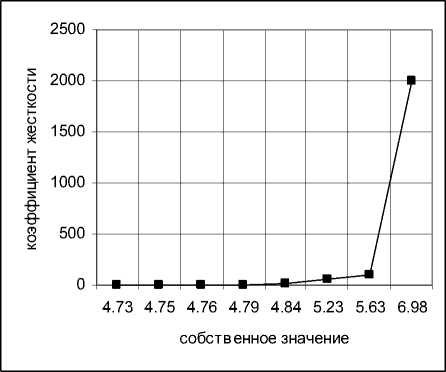
(б)

Рис. 1. Зависимость коэффициента B_l от собственных значений λ ₁ (а) и λ ₂ (б) при фиксированном значении B ₀

(а)

3. ПРИМЕРЫ

Применение метода рассмотрим непосредственно на примерах (для определенности примем, что l = 1).

Пример 1

Пусть λ ₁ = 1,56153060 , λ ₂ = 4,748887841 — собственные значения задачи (1), (4), соответствующие первым двум собственным частотам осесимметричных колебаний оболочки. Необходимо найти матрицу A с точностью до эквивалентных матриц, т. е. определить коэффициенты относительной жесткости упругих краевых ребер оболочки.

Система уравнений (6) перепишется следующим образом:

4,569260008 M ₁₃ + 9,485581903( M ₁₄ - M ₂₃) -14,40190378 M 24 = 0;

-115,3702577 M ₁₃ - 6404,394755( M ₁₄ - M ₂₃) +12693,41926 M ₂₄ = 0.

Решение системы имеет вид:

M ₁₃ = -0,5000000030 C ;

M ₁₃ = -0,5000000030 С ;                                                       (7)

M 14 — M 23 = C .

По решению разность M ₁₄ - M ₂₃ является произвольной постоянной. Так как M ₁₃ ^ 0, а M ₁₃ = - a ₀ b₀ , то а ₀ ^ 0 и b ₀ ^ 0. Разделим первую и вторую строки матрицы A соответственно на a ₀ и b ₀ . После этих преобразований (с точностью до эквивалентных матриц) матрицу A можно представить в виде

1 a 00

A =        ¹           .

( 0 0 - 1 b 1 )

Из последней матрицы следует, что M ₁₃ =- 1, значит C = 2 и M ₂₄ = 1 . Поскольку здесь M ₁₄ — M ₂₃ = a 1 + b 1 , M ₂₄ = a 1 b 1 , то из равенств a 1 + b 1 = 2 , a 1 b 1 = 1 по обратной теореме Виета имеем, что a 1 = 1 и Ь 1 = 1 . Значит

( 110 0 А

A =

0 0 0 - 1 1)

Далее по формулам (5) определим коэффициенты относительной жесткости упругих краевых ребер цилиндрической оболочки: B ₀ = 1, B l = 1.

Заметим, что относительные жесткости упругих краевых ребер определены верно. Числа 21 и 22, приведенные выше, совпадают с первыми двумя корнями частотного уравнения (6) при значениях a 0 = 1, a1 = 1, b0 = 1, b1 = 1, т. е. при M13 = — 1, M14 = 1, M 23 = — 1, M 24 = 1.

Пример 2

Пусть собственные значения задачи (1), (4) таковы: 2 1 = 1,750140001 ; 2 2 = 4,758314548 . Найдем матрицу A . В этом случае получаем решение системы (6) в виде:

M ₁₃ = —0,6666667028 C ;

M ₂₄ = 0,3333333288 C ;

M ₁₄ — M ₂₃ = C .

Поскольку M ₂₄ ^ 0 , то a 1 ^ 0 и b 1 ^ 0 . Проводя аналогичные, как в примере 1, рассуждения, получим что M ₂₄ = 1 , C = 3, M ₂₄ = 1 . Тогда из равенств a ₀ + b ₀ = 3 и a ₀ b ₀ = 2 находим, что a ₀ = 1, b ₀ = 2 или a ₀ = 2 , b ₀ = 1. Матрица A примет вид

A =

-■2 01

или A =

( 0 0

0 0 А

^{- 1 1} )

Значит, в этом случае имеем следующие коэффициенты относительной жесткости упругих краевых ребер цилиндрической оболочки: B ₀ = 1, B l = 2 или B ₀ = 2, B l = 1.

Относительные жесткости упругих краевых ребер определены верно. Числа 2 и 22, рассмотренные в примере, совпадают с первыми двумя корнями частотного уравнения (6) при значениях a0 = 1, a1 = 1, b0 = 2, b1 = 1 или M13 = —2, M14 = 1, M23 = —2 , M24 = 1.

Пример 3

Рассмотрим следующие собственные значения задачи (1), (4): A = 3,141592654 и

Л ₂ = 6.283185307 . Система (6) при этих значениях A i имеет решение:

M ₁₃ = 0,3238085777 • 10¹¹ C ;

M ₂₄ = 0,004236256425 C ;

M ₁₄- M ₂₃ = C .

Поскольку M ₁₄ - M ₂₃ является произвольной постоянной, а M ₁₃ значительно больше (на множитель 10¹¹ ) остальных неизвестных, то с достаточно большой точностью можно считать, что M ₁₃ = 1, а M ₂₄ = 0 , M ₁₄ — M ₂₃ = 0 . Так как M ₁₃ ^ 0, то a ₀ ^ 0 и b ₀ ^ 0. Проделав аналогичные, как в предыдущих примерах, действия с матрицей A , с точностью до эквивалентных матриц получим

1 a 00

• A =        ¹           .

• 0 0 - 1 bj

Из условий равенства нулю M ₂₄ и M ₁₄ - M ₂₃ имеем, что a ₁ = 0 и b ₁ = 0 . Тогда матрица A примет вид:

A =

^{0 0 0} ^

0 1 0 )

Значит, коэффициенты относительной жесткости упругих краевых ребер цилиндрической оболочки следующие: B0 = да и Bl = да .

Снова заметим, что относительные жесткости упругих краевых ребер определены верно. Числа A и A 2 , рассмотренные в примере, совпадают с первыми двумя корнями частотного уравнения (6) при значениях M ₁₃ = 1 , M ₁₄ = 0 , M ₂₃ = 0 , M ₂₄ = 0 . Этот пример показывает, что, зная первые две собственные частоты осесимметричных колебаний цилиндрической оболочки, рассмотренным методом можно определить и абсолютно жесткое закрепление ее краевых ребер.

Приведенные выше примеры показывают, что рассмотренным методом можно определить любые значения коэффициентов относительной жесткости упругих краевых ребер цилиндрической оболочки.

ЗАКЛЮЧЕНИЕ

Изменения численных значений частот колебаний оболочек свидетельствуют об изменениях жесткости закреплений их краевых ребер. Решенная задача определения относительной жесткости упругих краевых ребер цилиндрической оболочки позволяет диагностировать жесткость ее закреплений. Найденные формулы дают способ определения относительной жесткости по первым двум собственным частотам осесимметричных колебаний оболочки. Причем, рассмотренным методом можно определить и абсолютно жесткое закрепление краевых ребер. Кроме того, этот же метод может быть применен для диагностирования коэффициентов жесткости закреплений стержней, так как задача об изгибных колебаниях стержня сводится к спектральной задаче, аналогичной задаче (1).