Диапазон применения теоретических законов распределения

Определение показателей надёжности машин выполняется с целью оценки эффективности работы технических объектов в процессе эксплуатации [1]. Обоснованная методика обработки информации позволяет получить достоверные сведения о характере проявления отказов режимах и в последующем выявить причины их возникновения [2]. Исследование надёжности связано с организационноэкономическими трудностями и требует продолжительных эксплуатационных наблюдений, но при этом нужно обеспечить статистическую однородность партии изделий [3]. При обработке опытной информации сначала оценивают параметры закона распределения, а затем рассчитывают показатели надежности как функцию от оцененных параметров. Случайное возникновение неисправностей предопределяет также вероятностный характер оценки достоверности этого события [4]. Точность результатов характеризуется их близостью к действительным значениям в конкретных условиях испытания. Основными числовыми характеристиками, выражающими существенные особенности статистических данных, являются матема- тическое ожидание, дисперсия и коэффициент вариации случайной величины. Теоретический закон распределения выражает общий характер изменения показателя надёжности применительно к любой совокупности машин определённой марки. Для достижения точности оценок надёжности технических систем необходим обоснованный выбор теоретической функции распределения случайных величин. На практике используются ряд субъективных методов решения этой задачи: опыт эксплуатации аналогичных изделий, визуальный анализ исходной информации, диапазон рассеивания экспериментальных данных. В подавляющем большинстве случаев применяются следующие законы распределения: нормальный (ЗНР), Вейбулла (ЗРВ), Релея (ЗРР) и экспоненциальный (ЗЭР).

Одним из критериев предварительного выбора закона распределения является коэффициент вариации случайных величин. Однако этот параметр не гарантирует безусловное применение той или иной функции аппроксимации, поэтому необходимо дополнительное изучение границ использования теоретических законов с точки стве примера на рис. 1 показана дифференциальная функция из переходной зоны применения законов распределения (V = зрения обеспечения гарантированной точности результата. Для анализа взята ранее полученная информация по эксплуатаци-

Рис. 1. Вероятная плотность отказов при ЗНР (1), ЗРВ (2), ЗРР (3) и ЗЭР (4)

С изменением теоретического закона центр группирования отказов смещается относительно нормального распределения в сторону меньшей наработки. Характери- стиками нормального закона также являются коэффициенты асимметрии и эксцесса (рис. 2).

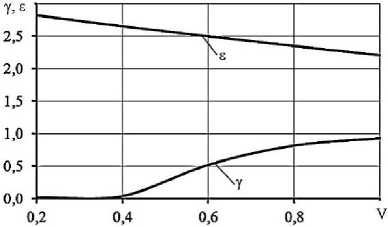
Рис. 2. Влияние коэффициента вариации на коэффициенты асимметрии (γ) и эксцесса (ε) нормального закона распределения

При V > 0,6 правосторонняя асимметрия и плоскостность распределения становятся значительными. Расчёты показали, что с повышением коэффициента вариации на 0.1 средний показатель надёжности снижается на 10…12%. Обработка исходной информации позволила выявить закономерности изменения относительной ошибки аппроксимации (рис. 3).

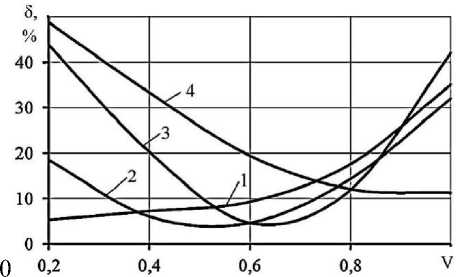
Рис. 3. Влияние коэффициента вариации на относительную ошибку аппроксимации при законах распределения: ЗНР (1), ЗРВ (2), ЗРР (3) и ЗЭР (4)

Для обеспечения ошибки исследования не более 10% целесообразно использование законов распределения при следующих значениях коэффициента вариации: V <  0,4 - нормальный, 0,4 « V « 0,6 -

Вейбулла, 0,6 <  V « 0,8 - Релея, V > 0,8 -экспоненциальный. Используя данные результаты можно уже на предварительном этапе назначать методику определения показателей надёжности технических систем.