Дидактический потенциал смешанного обучения математике обучающихся 7-9-х классов для формирования регулятивных универсальных учебных действий

DOI:

Шкерина Людмила Васильевна - доктор педагогических наук, профессор, КГПУ им. В.П. Астафьева; ORCID: ; Scopus Author ID: 57193439041; e-mail:

П остановка проблемы . Смешанное обучение – один из ключевых трендов современного образования, формирующий новое педагогическое мировоззрение. Понятие «смешанное обучение» в отечественной научной литературе достаточно молодое и вызывает большой интерес среди ученых, методистов и педагогов-практиков. В последние годы наблюдается, увеличение количества школ, в которых реализуется одна или несколько моделей смешанного обучения. Однако в период пандемии вопрос, связанный со смешанным обучением, стал одним из приоритетных, когда большинство российских школ были вынуждены перейти на электронное обучение с применением дистанционных образовательных технологий, а затем определиться с системой обучения, которая позволяла бы решать различные педагогические задачи образовательного процесса, отвечающие требованиям федеральных государственных образовательных стандартов (далее – ФГОС).

Изучение смешанного обучения в отечественной педагогике начиналось с системы высшего образования. В результате появился ряд научных работ, в том числе и диссертационных, освещающих данный вопрос1, 2, 3, 4, 5. Позже стали появляться публикации, в которых описывался опыт внедрения смешанного обучения в школу. В 2012–2013 гг. впервые в российском образовании был начат инновационный проект по апробации моделей смешанного обучения на основе ресурса Некоммерческое партнерство (НП) «Телешкола». Внедрением смешанного обучения в российские школы активно занимается Центр смешанного обучения МГПУ под руководством Н.В. Андреевой. Выводы о ходе реализации смешанного обучения основаны на результатах исследования Института К. Кристенсена, а также практического опыта отечественных педагогов.

Активное внедрение смешанного обучения в учебный процесс породило большое количество вопросов не только общей направленности для всей образовательной системы, но и в рамках отдельных предметов. Представляет интерес включение смешанного обучения в процесс математической подготовки обучающихся 7–9-х классов и его преимущества для реализации требований ФГОС основного общего образования, в частности формирования РУУД. Многие исследователи придерживаются мнения, что РУУД являются системообразующими среди универсальных учебных действий, благодаря которым обучающиеся способны организовать собственную учебную деятельность, обеспечивающую достижение планируемых результатов. Опыт преподавания математики в период пандемии показал, что обучающиеся испытывали трудности с постановкой целей и планированием учебной деятельности при смене пространства обучения с реального на виртуальное. При синхронном и асинхронном форматах обучения появилась потребность обратиться за помощью в выполнении полного или частичного объема заданий, в контроле времени, оценивании своих результатов и важности корректировки для дальнейшего освоения учебного материала. Перед педагогами возникла необходимость поиска решения проблем, осмысления ресурсов смешанного обучения математике для формирования РУУД обучающихся, способствующих определению путей выхода из ситуации. Однако научных работ, описывающих теоретические и практические положения формирования РУУД обучающихся 7–9-х классов в условиях использования смешанного обучения математике, содержащих разные точки зрения, недостаточно для принятия общего решения. Проведенный анализ выявил наличие проблемы: использование какой совокупности методов, средств, форм и способов в условиях смешанного обучения математике обеспечит формирование РУУД обучающихся 7–9-х классов.

Цель статьи – выявить дидактический потенциал смешанного обучения математике для формирования РУУД обучающихся 7–9-х классов.

Методологию исследования составили: теоретические положения развития информационных технологий и информатизации образования (М.П. Лапчик, Л.П. Мартиросян, И.В. Роберт, Е.С. Полат и др.); основные идеи смешанного обучения (Н.В. Андреева, В.И. Блинов, К. Бонк, Ч. Грэхем, Е.Ю. Есенина, И.С. Сергеев, Х. Стейкер, М. Хорн и др.); системно-деятельностный подход (Л.С. Выгодский, А.Н. Леонтьев, П.Я. Гальперин, Д.Б. Эльконин, В.В. Давыдов и др); исследования в области формирования РУУД (О.В. Берсенева, Л.И. Боженкова, М.В. Егупова, Е.Н. Пе-ревощикова, О.В. Тумашев, Л.В. Шкерина и др.); анализ научных публикаций по обозначенной проблеме и образовательной практике.

Обзор научной литературы. С каждым годом смешанному обучению посвящается все больше научных статей и монографий, происходит активное обсуждение в рамках научных конференций различного уровня.

С течением времени содержание понятия «смешанное обучение» развивалось и уточнялось зарубежными и отечественными учеными. Среди зарубежных исследователей свой вклад внесли Д. Кларк (D. Clarc), Дж. Берзин (J. Ber-sin), К.Р. Грэхем (C.R. Graham), М. Хорн (M. Horn), Х. Стейкер (H. Staker), П. Валиатан (P. Valiathan), Дж. Уотсон (J. Watson) и др. [Фандей, 2011]. Однако одно из педагогически емких определений предложили Х. Стейкер и М. Хорн: «Смешанное обучение – это формальная образовательная программа, в которой ученик учится:

– по крайней мере, частично через онлайн-обучение, с некоторыми элементами контроля учащихся над временем, местом, путем и/или темпом;

– по крайней мере, частично в контролируемом традиционном формате не дома;

– условия обучения каждого ученика в рамках курса или предмета связаны между собой для обеспечения интегрированного учебного опыта» [Staker, Horn, 2012]. Как отмечает Н.В. Андреева, определение «смешанного обучения», сформулированное Х. Стейкер и М. Хорном, отличается от определения К.Р. Грэхема «акцентом на формировании учебной самостоятельности в онлайн-среде, а также интеграцией опыта, полученного онлайн и оффлайн» [Graham, 2006; Андреева, 2020]. Подчеркнем, что, анализируя работы зарубежных авторов, можно утверждать также, что одной из составляющих понятия «смешанное обучение», помимо контроля времени, темпа и маршрута освоения учебного материала, является автоматизированная помощь для достижения поставленных целей.

В статье В.И. Блинова, Е.Ю. Есениной, И.С. Сергеева рассматриваются аспекты смешанного обучения, связанные с его организацией в образовательном учреждении и совместной деятельностью обучающихся и педагога. Авторы проводят анализ существующих определений «смешанного обучения», а также подходов к классификации моделей смешанного обучения [Блинов, Есенина, Сергеев, 2021]. Во многих исследованиях, посвященных смешанному обучению в образовательных учреждениях, используются классификации Ю. Духнич, Э.А. Кадыровой, В.А. Фандей, Д. Кларка, М. Хорна и Х. Стей-кер, коллектива авторов НП «Телешкола» [Лу-ченкова, Носков, Шершнева, 2015]. М.А. Иванов, Н.В. Ершова на основе анализа опыта в период пандемии делают вывод, что смешанное обучение может быть реализовано по четырем организационным моделям в зависимости от наполняемости образовательного учреждения и количества смен (Иванов, Ершова, 2021). Для эффективности планируемого результата при выборе модели смешанного обучения из любой классификации важно учитывать наличие элементов персонализации, побуждающих самостоя-

тельно определять свои учебные цели и способы достижения, индивидуализации, дифференциации, возможности для каждого обучающегося нести ответственность за собственный процесс обучения, осуществление регуляции темпа и ритма освоения учебного материала.

В работах Н.В. Андреевой, Е.К. Васина, О.Б. Даутовой Т.В. Долговой, Е.Ю. Игнатьевой, М.Л. Кондаковой, Е.А. Корниловой, Н.В. Лю-бомирской и др. изучаются организационнометодические аспекты смешанного обучения в школе. Среди дидактических особенностей исследователи отмечают оптимальное сочетание традиционной и электронной форм обучения за счет их преимуществ, преобладание индивидуальной работы, способствующей развитию учебной самостоятельности, способности к рефлексии и самоанализу, формированию навыков для продолжения образования в будущем [Долгова, 2017; Марголис, 2018; Андреева, 2020; Блинов, Есенина, Сергеев, 2021].

Анализируя работы, посвященные различным моделям смешанного обучения, можно сделать вывод о том, что многие исследователи чаще всего уделяют внимание ротационным моделям, а именно «перевернутому обучению» и «ротации станций». В публикациях [Корнилова, Стрижаков, 2016; Смыковская, Машевская, Сидунова, 2017; Андреева, 2018; Любомирская, Рудик, Хоченкова, 2019; Шульгина, 2021] авторы описывают использование ротационных моделей на основе практического опыта, отмечают достоинства и недостатки. Подчеркнем, что наличие активных и интерактивных методов обучения – обязательное условие для реализации эффективного смешанного обучения [Нагаева, 2016; Erbil, 2020; Чошанов, 2022]. Довольно часто стали встречаться рекомендации для учителей, работающих по определенной модели смешанного обучения [Shu-Chen Cheng, Gwo-Jen Hwan, Chiu-Lin Lai, 2020]. Отметим, что на сайте Центра смешанного обучения появляется полезная информация для учителей.

Работы, посвященные смешанному обучению математике, в последнее время стали появляться чаще. Так, например, в работах [Дербуш,

Скарбич, 2021; Костюченко, 2021] предложены способы организации исследовательской деятельности обучающихся основной и старшей школы, формирования математических понятий. Среди этих работ еще реже встречаются те, которые посвящены теме исследования – формированию РУУД обучающихся 7–9-х классов.

В работе [Гиматдинова, 2020] приводится краткое описание тех РУУД, которые могут формироваться у обучающихся 7–9-х классов при использовании ротационных моделей. Более подробно Т.П. Фисенко на примере одной из моделей смешанного обучения анализирует возможности развития составных компонентов РУУД [Фисенко, 2021].

Анализ современного опыта организации смешанного обучения, в том числе и на уроках математики, позволил интегрировать формы обучения, методы, приемы, способы, средства как дидактический потенциал обучения математике для формирования РУУД обучающихся 7–9-х классов и представить в виде специальной карты-схемы (рис.).

Результаты. Под смешанным обучением математике будем понимать обучение, интегрирующее в себе очное обучение (прямое личное взаимодействие между участниками образовательного процесса), электронно-дистанционное обучение (взаимодействие между участниками образовательного процесса посредством электронного обучения с применением дистанционных технологий), самообразование. Смешанное обучение может обеспечивать непрерывный процесс обучения, погружая обучающихся в реальную и виртуальную среду при определенно заданных условиях.

Дидактический потенциал представляет «совокупность методов, средств, форм и способов обучения, обеспечивающих эффективность достижения целей обучения с учетом содержания, закономерностей и принципов» [Берсенева, 2016]. В карте дидактического потенциала смешанного обучения для формирования РУУД обучающихся 7–9-х классов представлен комплекс методов, средств, форм, приемов, форматов обучения в зависимости от модели смешанного обучения. Учитывая специфику обучающихся 7–9-х классов, считаем, что наиболее подходящими являются такие модели, как «Перевернутое обучение», «Ротация станций», «Ротация лабораторий», «На выбор».

«Перевернутое обучение» – модель смешанного обучения, при которой ознакомление с учебным материалом происходит в домашних условиях, а в классе обучающиеся обсуждают и закрепляют материал под руководством учителя.

В случае «Ротации станций» обучающиеся в классе делятся на несколько групп и занимаются посменно под руководством учителя разными видами учебной деятельности, включая работу с цифровыми образовательными ресурсами.

«Ротация лабораторий» предполагает, что основная часть занятий происходит в классе, а на один урок обучающиеся перемещаются в компьютерный класс и индивидуально работают в онлайн-среде. При этом они могут изучать новый материал, закреплять пройденное, осуществлять тренировку навыков, работать над собственным проектом.

Модель смешанного обучения «На выбор», скорее всего, подойдет для факультативных занятий или занятий в рамках подготовки к экзамену, при которой происходит более детальное и углубленное изучение некоторых разделов математики, не входящих в рамки школьной программы.

На рисунке представлена карта-схема дидактического потенциала смешанного обучения математике для формирования РУУД обучающихся 7–9-х классов.

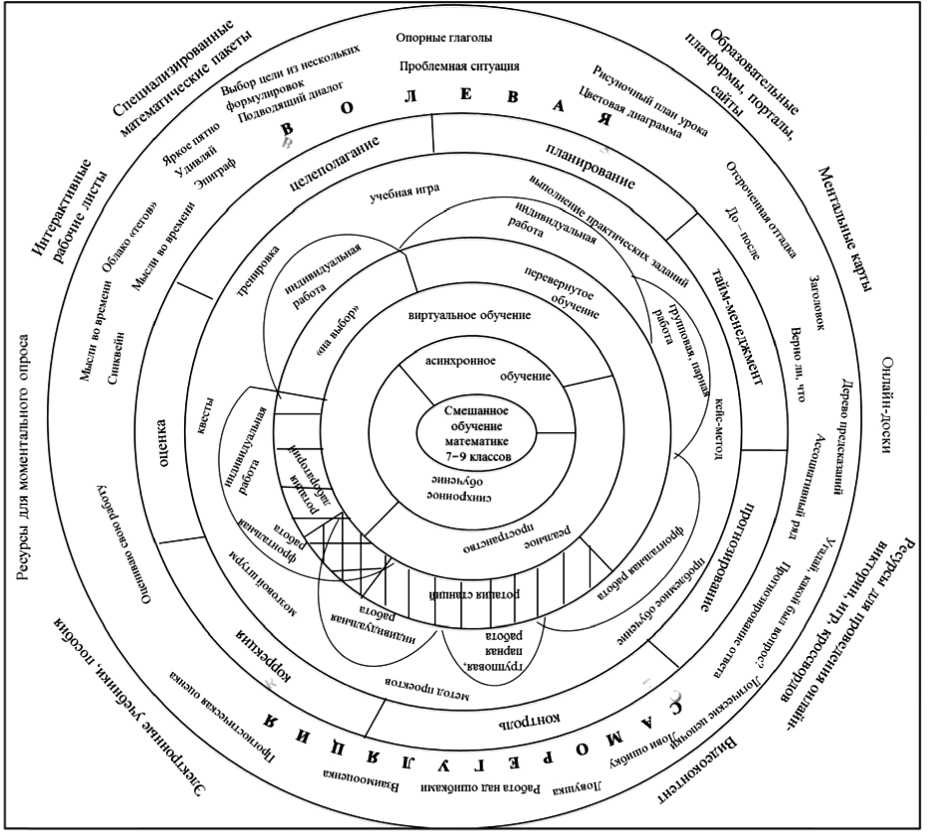
Рис. Карта-схема дидактического потенциала смешанного обучения математике для формирования регулятивных универсальных учебных действий обучающихся 7–9-х классов Fig. Schematic map of didactic potential in blended learning of mathematics for development of regulatory universal educational actions among students in grades 7–9

КРАСНОЯРСКОГО ГОСУДАРСТВЕННОГО

ПЕДАГОГИЧЕСКОГО УНИВЕРСИТЕТА им. В.П. АСТАФЬЕВА

s щ

Смешанное обучение математике обучающихся 7–9-х классов может проходить в двух форматах обучения – синхронном и асинхронном. Синхронное обучение происходит как в реальном, так и виртуальном пространстве, асинхронное – в виртуальном. Реализация выделенных моделей смешанного обучения подразумевает сочетание определенных пространств и форматов. Для достижения предметных результатов, а также формирования РУУД педагог выбирает комбинацию форм работы, методов, приемов и средств.

Рассмотрим на примере модели «Перевернутое обучение», как могут сочетаться различные форматы, формы, методы и средства для формирования РУУД, представленные на карте-схеме.

Тема: «Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии».

В качестве домашнего задания обучающимся предлагается ряд заданий по изучению новой темы. Они все собраны в Google-форме по ссылке: В документе содержится указанная последовательность заданий.

• 1.    В качестве введения в тему просмотреть короткий видеоролик по ссылке: https://youtu . be/ARntHLRYdV4 – и ответить на вопросов, встречались ли ранее обучающиеся с новым понятием.

• 2.    Просмотреть видео по новой теме по ссылке: https://youtu.be/F0RqBWKEq9Q – и ответить на ряд вопрос на понимание учебного материала.

• 3.    Для первичного закрепления материала выполнить задания по двум ссылкам: https:// learningapps.org/watch?v=pizy5ebaa22 и https:// learningapps.org/watch?v=pt7ahp27222.

• 4.    В заключение предлагается ознакомиться с фрагментами задач на арифметическую прогрессию из таких наук, как биология, физика и химия. Можно придумать свои примеры из других школьных предметов, где также встречается арифметическая прогрессия.

На данном этапе освоения учебного материала обучающиеся, во-первых, должны распределить собственное время на выполнение задания, предложенное учителем. Ориентиром может являться момент времени, когда было отправлено задание в журнал (с обязательным наличием дедлайна сдачи работы) и время отправления формы учителю. Во-вторых, после отправки формы обучающийся имеет возможность проконтролировать правильность выполнения заданий. В-третьих, при работе с упражнениями на платформе LearningApps имеется возможность не только осуществлять контроль своей деятельности, но и корректировать ее в случае указания ошибок. Обратим внимание, что в зависимости от готовности к самостоятельному изучению материала обучающийся принимает решение, какие задания ему выполнять, а какие – нет. При выполнении домашнего задания допускается обращение за помощью к своим одноклассникам, учителю, в Интернет.

В условиях очного формата может быть такое развитие событий, при котором большинство обучающихся не выполнили задание или выполнили многие задания неправильно, или в специальной строке записали большое количество вопросов. Об этом учитель узнает по количеству ответов в Google-форме. В этом случае учителю необходимо еще раз вернуться к обсуждению учебного материала, воспользоваться карточками для коррекции знаний. Если большинство обучающихся выполнили задание, то можно приступать к закреплению учебного материала, используя активные методы обучения. В качестве примера предлагаем использовать метод кооперативного взаимообучения, который заключается в постоянной взаимопомощи и взаимопроверке работ, предложенных учителем, взаимоисправлении ошибок.

На данном этапе освоения учебного материала, во-первых, обучающиеся под руководством учителя должны сформулировать цель и задачи урока, а каждый обучающийся должен зафиксировать для себя собственную цель. В соответствии с предложенными заданиями обучающийся должен спланировать, в какой последовательности он будет их выполнять. При этом используемый метод обучения позволит обучающимся предвидеть возможные трудности при выполнении задания и оценить необходимость воспользоваться помощью. А сама суть метода создает ситуацию контроля и коррекции собственной учебной деятельности.

Заключение. Методология проведенного исследования позволила выявить и наглядно представить дидактический потенциал смешанного обучения математике для формирования РУУД обучающихся 7–9-х классов в виде карты-схемы, ориентированной на основные модели смешанного обучения. С опорой на эту карту-схему можно разрабатывать методическое обеспечение обучения математике в любой модели смешанного обучения, ориентированного на формирование РУУД обучающихся. Разработанная карта-схема может быть адаптирована с учетом специфики предметного содержания других дисциплин и использована для проектирования процесса формирования РУУД обучающихся в процессе смешанного обучения.