Dielectric properties of solid solutions of manganese chalkogenides substituted by ions of gadolinium

Introduction. Materials in which the interrelation of magnetic and electrical properties manifests itself [1], that is, magnetoelectrics and multiferroics, [2] are of interest both from the fundamental and from the applied point of view. Particular attention is attracted to materials that exhibit magnetoelectric properties at room and higher temperatures in connection with practical applications in microelectronics for recording and storing information. Such studied materials include bismuth ferrite BiFeO 3 [3]. The giant magneto-capacitance effect was observed in LuFe 2 O 4 [4] at room temperature and is explained by the charge fluctuation with different spin in Fe²⁺ and Fe³⁺ ions as a result of removing the degeneracy between two types of charge order by an external magnetic field. The dependence of the orbital magnetic moments on the polar distortions induced by the electric field gives an “ionorbit” contribution to the magnetoelectric response [5].

At a high level of doping, an orbitally disordered state may arise, which is energetically favorable in comparison with antiferroorbital ordering due to a decrease in the kinetic energy. Analogously to disordered spin systems, when ferromagnetic polarons exist in the paramagnetic region [6], in the high-temperature range, the orbital polarons contribute to the kinetic properties of such systems [7]. The shape of the orbital polarons depends on the configuration of the electronic orbitals. In the presence of an orbital magnetic moment, for example, for electrons in t _{2 g} -states, the orbital polarons have a magnetic moment. In this case, the energy of the orbital polaron depends on the direction and magnitude of the external magnetic field. The anisotropy of the electron density distribution in the lattice leads to anisotropy of the dielectric permittivity, which can be controlled by a magnetic field.

In electrically non-uniform systems, the Maxwell– Wagner effect [8] and contact effects can lead to giant values of dielectric permittivity and dielectric relaxation in the absence of dipole relaxation [9]. The Maxwell-Wagner effect can also induce magneto-capacitance in the absence of interaction between the magnetic and electrical subsystems, provided the magnetoresistance exists in the material [10]. Such effects clearly demonstrate that the presence of magneto-capacitance is not sufficient to classify these compounds as multiferroics. On the other hand, the magneto-capacitance without a magnetoelectric coupling can be more practical for technological applications as the existence of a long-range magnetic order is not required.

An electrically non-uniform system with orbital degeneracy is obtained by replacing divalent manganese ions with trivalent gadolinium ions. Thus, the starting compounds of manganese selenide and gadolinium selenide are, respectively, a semiconductor and a degenerate semimetal whose electrical resistance is 10⁶–10⁹ times different from each other [11]. Gadolinium selenide and manganese selenide have an antiferromagnetic structure of the second ordering type with Neel temperature T N = = 63 K [12] and T N = 137 K [13]. The spin-orbit and the Jahn-Teller interaction remove the degeneracy of the t 2 g electronic states and induce splitting of the electron spin excitation spectrum. As a result, dielectric properties can be controlled by electric and magnetic fields.

The aim of this paper is to establish the role of anions and the effect of cation substitution on the magnetoelectric coupling in orbital-degenerate electronic states in Gd x Mn 1– x A solid solutions (A = S, Se).

Experimental results and their discussion. Synthesis of solid solutions Gd _x Mn_{1– x} A (A = S, Se) and their certification were described in detail earlier in [14]. The magnetocapacitance effect δε H = (ε( H ,T) – ε (0, T )) / ε (0, T )) is determined by the investigation of the complex dielectric permittivity. The spectral and temperature dependences of dielectric constants can be used to detect the dipole electric moment and to determine its characteristics, even when it is a question of a local dipole moment in small clusters without the presence of long-range order. Dielectric properties also reflect the information about charge transport and charge ordering processes. The response of the dielectric properties to the action of the magnetic field will make it possible to determine the basic mechanisms that determine the behavior of the dielectric and electric transport properties.

The capacitance and tangent of the dielectric loss angle (tg δ) were measured on the AM-3028 component analyzer in the temperature range 90–450 K without a magnetic field and in the magnetic field H = 8.6 kOe. The magnetic field was applied parallel to the plates of a flat capacitor. Fig. 1 shows the temperature dependences of the real Re (ε) and imaginary Im (ε) = tg δRe (ε) parts of the dielectric constant of the sample Gd 0.04 Mn 0.96 S. Heating the sample causes a sharp increase in dielectric losses, the imaginary part of the dielectric constant increases threefold, and the imaginary part increases by 5 % at T = 102 K. As the temperature increases, the dielectric constant gradually increases and decreases sharply at T = = 172 K with a slight increase. The change in the permittivity Gd 0.04 Mn 0.96 S within one percent in the magnetic field was not detected. A sharp change in the dielectric permittivity is due to structural distortions of the lattice from the cubic to the rhombohedral structure observed in the non-stoichiometric manganese sulfide at T = 168 K.

Fig. 2 shows the temperature dependences of the real Re (ε) and imaginary Im (ε) = tg δRe (ε) parts of the dielectric permittivity of the sample Gd0.05Mn0.95Se. In the temperature range 220–330 K, the real part of the dielectric permittivity increases twofold and shifts with increasing frequency towards higher temperatures. The temperature of the maximum of the dielectric losses increases with increasing frequency and is described by a nonlinear function of the logarithm of frequency. The frequency dependence of the complex dielectric permittivity does not correspond to the Debye and Cole-Cole models, which describe the dielectric properties of homogeneous systems with the exponential dependence of the relaxation of the polarization parameter.

The frequency of the dielectric relaxation corresponding to the maximum of Im (ε) has an activation character and is well described by the function lnω = A exp (–∆ E / kT ) (fig. 2, b ), where the activation energy ∆ E = 0.051 eV and the exponential satisfies the condition exp (–Δ E / kT ) << 1 at T < 350 K. Below this temperature, the relaxation frequency and time (τ) can be represented as:

го = B exp

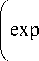
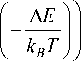
= B I 1 + exp

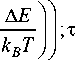
^T 0

1 + exp

A E )^. k B T J

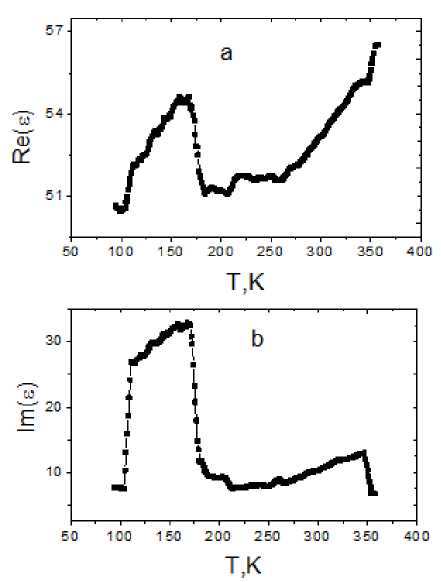
Fig. 1. Real ( a ) and imaginary ( b ) components of the dielectric permittivity for sample Gd 0.04 Mn 0.96 S at the frequency of 10 kHz from the temperature

Рис. 1. Реальная ( а ) и мнимая ( b ) компоненты диэлектрической проницаемости для образца Gd 0,04 Mn 0,96 S на частоте 10 кГц от температуры

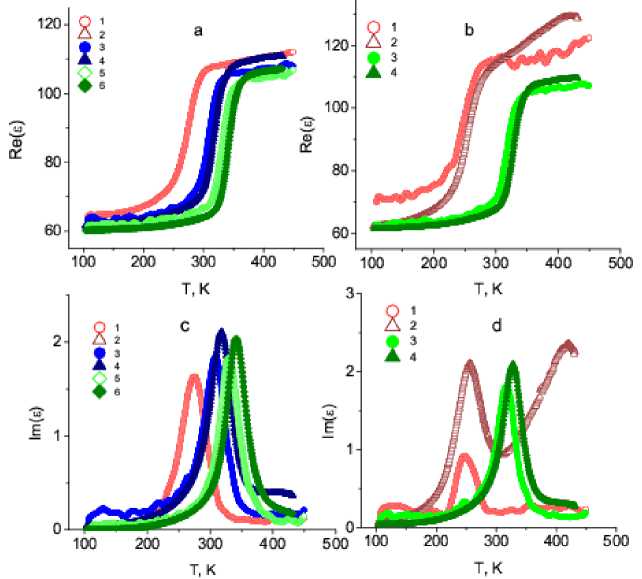
Fig. 2. Real Re (ε) ( a , b ) and imaginary Im (ε) ( c , d ) ( c , d ) components of the dielectric permittivity of the sample Gd 0.05 Mn 0.95 Se in the magnetic field H = 0 ( 1 , 3 , 5 ), H = 8 kOe ( 2 , 4 , 6 ) at frequencies ω = 5, 50, 300 kHz ( a , c ), ω = 1, 100 kHz ( b , d ) from the temperature

Рис. 2. Реальная Re(ε) ( a , б ) и мнимая Im(ε) ( в , г ) компоненты диэлектрической проницаемости образца Gd_0,05Mn_0,95Sе в магнитном поле H = 0 ( 1 , 3 , 5 ), Н = 8 кЭ ( 2 , 4 , 6 ) на частотах ω = 5, 50, 300 кГц ( a , в ), ω = 1, 100 кГц ( б , г ) от температуры

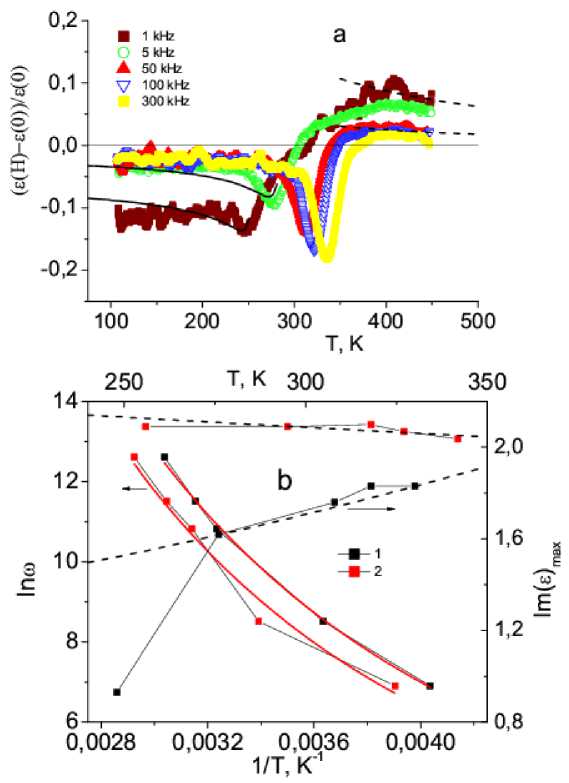
Fig. 3. Magnet capacity δε Gd_0.05Mn_0.95Sе at frequencies ω = 1, 5, 50, 100, 300 kHz in the magnetic field H = 8 kOe for the composition with x = 0.05 of the temperature ( a ); logarithm of the relaxation frequency from the reciprocal temperature without a field ( 1 ) and in the magnetic field H = 8 kOe ( 2 ), adjustment function ( 1 ) (left axis) ( b ). The maximum of Im(ε) as a function of temperature. Adjustment functions Im(ε) max = AN pe + BN ph (dashed line) (right axis)

Рис. 3. Магнитоемкость δε Gd 0,05 Mn 0,95 Sе на частотах ω = 1, 5, 50, 100, 300 кГц в магнитном поле Н = 8 кЭ для состава с х = 0,05 от температуры ( а ); логарифм частоты релаксации от обратной температуры без поля ( 1 ) и в магнитном поле Н = = 8 кЭ ( 2 ), подгоночная функция ( 1 ) (левая ось) ( б ). Максимум Im(ε) от температуры. Подгоночные функции Im(ε)_max = AN_pe + + BN_ph (пунктирная линия) (правая ось)

The activation energy in formula (1) corresponds to the polaron energy (εp) relative to the chemical potential (μ), –ΔE = εp – μ < 0. The relaxation time is proportional to the polaron density τ ∞ Np. If the polaron energy exceeds the chemical potential εp > μ, then this is a polaron of the hole type Nph = A / (1 + exp (ΔE / kT)). The imaginary component of the dielectric permittivity, due to scattering of polarons by optical phonons, is proportional to Im (ε)max ∞ (Npe + Nph). The maxima of the dielectric losses increase with increasing frequency and temperature without a magnetic field and smoothly decrease in the magnetic field (fig. 3, b) as a result of the restructuring of the electronic structure in a magnetic field. So in the zero field, the spectral weight of polarons with a hole-type conductivity with the ratio Nph / Npe = 5.5 prevails, and in a magnetic field – the spectral weight of polarons with the electron type Npe / Nph = 2.3, which qualitatively describes the experimental results (fig. 3, b).

The temperature at which the dielectric permittivity increases sharply and the maximum of the dielectric losses is observed, shifts to high temperature area in a magnetic field. The activation energy increases by 5 % in a magnetic field of 8 kOe. The magneto-capacity δε = = (ε ( H ) – ε (0)) / ε (0) for the composition with х = 0.05 is presented in fig. 3, a . When heated, the magneto-capacity changes sign and decreases with increasing frequency.

Having divided all the charge carriers into two groups – bound and free charges, we can write the dielectric permittivity of the medium as the sum of the dielectric permittivity of the “lattice” and the contribution of free carriers. Outside the absorption bands, the imaginary part of the permittivity of bound charges (lattices) is usually neglected. The ensemble of carriers was considered as a sum of particles that do not interact with one another. In semiconductors with electron doping, the electrons are delocalized in a certain region and the delocalization radius increases with increasing temperature. We represent the functional dependence in the form of a correlation radius ξ = A / (1 – T c / T ), where T c is the temperature of charge ordering of electrons in t 2 g orbitals. Localized electrons induce local ion displacements and lead to local polarization with an effective dipole moment, whose dynamic susceptibility is described in the Debye model.

With decreasing temperature at T _g as a result of the interaction between dipoles through the lattice, local dipoles

“freeze”. The relaxation time of dipoles is described by the Arrhenius function: τ g = τ 0 exp (Δ E / kT ), where Δ E is the activation energy. The dielectric susceptibility can be written as:

Re(χ)/N = χL0 + χ0/(1 + (ωτg)2) + В/(1 – Tc/T), (2) Im(χ)/N = χ0ωτg /(1 + (ωτg)2) + χ0ωτc /(1 + (ωτc)2), where χL0 is the temperature-independent contribution to the susceptibility; χ0 is the static susceptibility of the dipoles; B is the constant; τg is the relaxation time of the dipoles at the freezing point; τc is the relaxation time of the electric charges upon transition to the orbital charge ordering, τc = A / χz = A / (1 – Tc / T)zν, where z is the dynamic index, and ν is the index of the correlation radius (ν = 1). The contribution of free charge carriers is neglected, since the value of σIm of conductivity is several orders of magnitude greater than the conductivity at constant current.

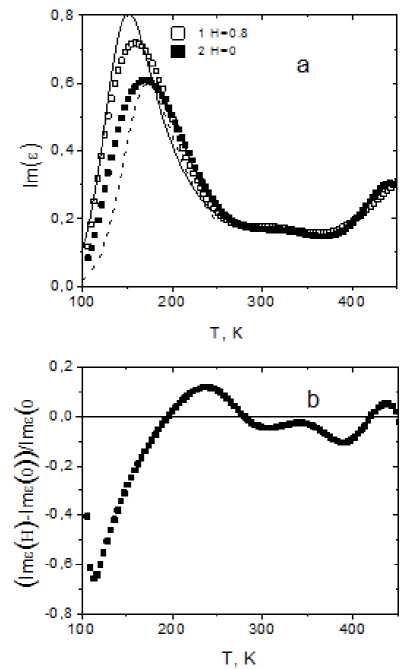
Fig. 4. Imaginary part of the dielectric permittivity ( a ) of a solid solution Gd_0.2Mn_0.8S, measured at a frequency of 10 kHz, without a field ( 1 ) and in the magnetic field H = 8 kOe ( 2 ) as a function of temperature. Adjustment function (1b) with activation energy of 900 К ( 3 ), 1050 ( 4 ), z v = 2 ( a ). Relative change of the imaginary part of the dielectric permittivity in a magnetic field from the temperature ( b )

Рис. 4. Мнимая часть диэлектрической проницаемости ( а ) твердого раствора Gd 0,2 Mn 0,8 S, измеренной на частоте 10 кГц, без поля ( 1 ) и в магнитном поле Н = 8 кЭ ( 2 ) от температуры. Подгоночная функция (1b) c энергией активации 900 К ( 3 ), 1050 ( 4 ), zv = 2 ( a ). Относительное изменение мнимой части диэлектрической проницаемости в магнитном поле от температуры ( б )

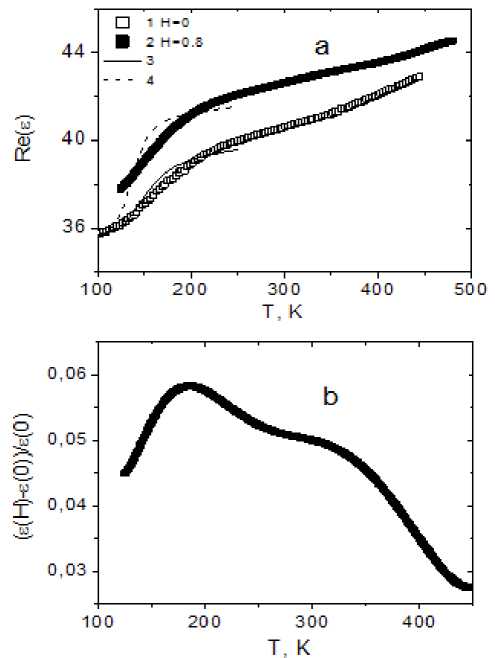
Fig. 5. The real part of the dielectric permittivity ( a ) of a solid solution Gd_0.2Mn_0.8S, measured at the frequency of 10 kHz without a field ( 1 ) and in the magnetic field H = 8 kOe ( 2 ) as a function of temperature. Adjustment function (1a) with activation energy of 900 К ( 3 ), 1050 ( 4 ), zv = 2 ( a ). The magnetic capacity in a magnetic field is H = 8 kOe of temperature ( b )

Рис. 5. Реальная часть диэлектрической проницаемости ( а ) твердого раствора Gd 0,2 Mn 0,8 S, измеренной на частоте 10 кГц без поля ( 1 ) и в магнитном поле Н = 8кЭ ( 2 ) от температуры. Подгоночная функция (1a) c энергией активации 900 К ( 3 ), 1050 ( 4 ), zv = 2 ( a ). Магнитоемкость в магнитном поле H = 8 кЭ температуры ( б )

When the concentration of gadolinium ions exceeds the concentration of percolation x c = 0.16, the resistance varies within one order and has a minimum at T = 325 K in the temperature range 100 K <  T < 500 K in a solid solution Gd x Mn 1– x S. In a magnetic field, the resistance also increases and the minimum in the temperature dependence shifts toward high temperatures to T = 380 K. The temperature dependence of the magnetoresistance changes sign from positive to negative at T = 320 K and disappears at the temperature of 475 K. In this solid solution, there are two conduction channels for gadolinium ions and for the interface of Mn–Gd ions. Therefore, the electronic contribution to the susceptibility should be taken into account.

Regardless of the type (electrons or holes), free charge carriers reduce the real part of the dielectric permittivity. This decrease becomes more significant with increasing the concentration and decreasing effective mass of charge carriers. The decrease in the dielectric permittivity by free charge carriers is associated with their inductive contribu- tion to the result of the interaction of the alternating field with matter.

For the composition Gd 0.2 Mn 0.8 S, the dielectric permittivity is due to localized electrons in the sublattice of manganese ions and conduction electrons in the gado-linene subsystem. Conductivity at constant current varies by a factor of three, and the imaginary part of the dielectric susceptibility changes by an order of magnitude in the temperature interval 100–400 K (fig. 4). The temperature dependence of Im (ε (ω)) has two maxima at T = 170 K and T = 442 K. In the magnetic field H = 8 kOe, the low-temperature peak shifts toward high temperatures to T = 170 K (fig. 4). Dielectric losses decrease in a magnetic field, except for the temperature range 194–279 K and in 417–451 K (fig. 4). The low-temperature maximum in the dielectric permittivity at T = 170 K is described in the localized electron (2) model with the freezing of dipole moments with an activation energy Δ E = 800 K without a magnetic field and in the magnetic field Δ E = 1000 K. The adjustment function describes the experimental data in fig. 4.

Im(£>                       Re(t)

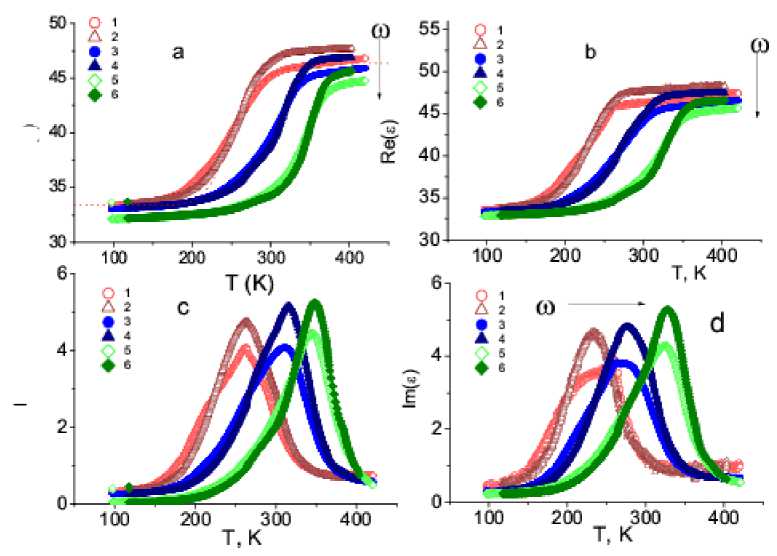
Fig. 6. Real Re (ε) ( a , b ) and imaginary Im (ε) ( c , d ) parts of the dielectric permittivity of the sample Gd 0.2 Mn 0.8 Se without a field ( 1 , 3 , 5 ) and in the magnetic field H = 8 kOe ( 2 , 4 , 6 ) at frequencies ω = 5, 50, 300 kHz ( a , c ), ω = 1, 10, 100 kHz ( b , d ) as a function of temperature

Рис. 6. Реальная Re(ε) ( a , б ) и мнимая Im(ε) ( в , г ) части диэлектрической проницаемости образца Gd_0.2Mn_0.8Sе без поля ( 1 , 3 , 5 ) и в магнитном поле Н = 8 кЭ ( 2 , 4 , 6 ) на частотах ω = 5, 50, 300 кГц ( a , в ), ω = 1, 10, 100 кГц ( б , г ) от температуры

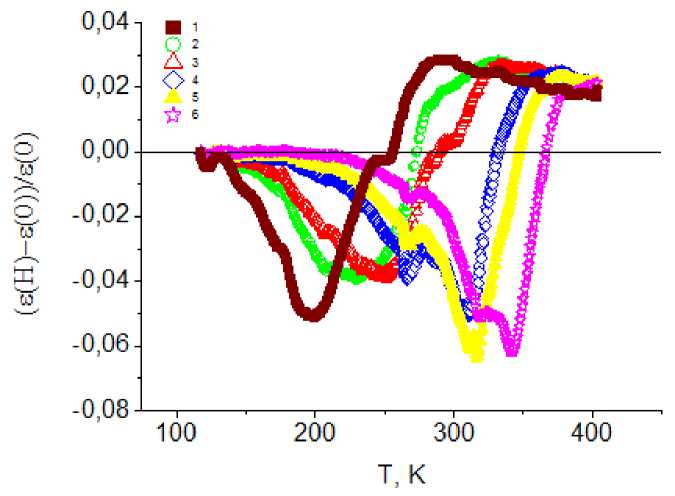
Fig. 7. The magnetic capacity δε Gd 0.2 Mn 0.8 Se at the frequencies ω = 1( 1 ), 5( 2 ), 10( 3 ), 50( 4 ), 100( 5 ), 300 ( 6 ) kHz in the magnetic field H = 8 kOe for a composition with x = 0.2 of temperature

Рис. 7. Магнитоемкость δε Gd 0,2 Mn 0,8 Se на частотах ω = 1( 1 ), 5( 2 ), 10( 3 ), 50( 4 ), 100( 5 ), 300( 6 ) кГц в магнитном поле Н = 8 кЭ для состава с х = 0,2 от температуры

This maximum can be associated either with the reorientation of electric dipoles, or with charge transfer between the nonequivalent positions in the crystal lattice of the material, which in a sense is equivalent to the reorientation of electric dipoles. The growth of the magnetoresistance in Gd_0.2Mn_0.8S [15] in a magnetic field disproves the version associated with charge transfer. The decrease of dielectric losses in a magnetic field is associated with redistribution of the electron density over t 2g orbitals, for example, between d zx d zy , which is equivalent to the rotation of an electric dipole. Partial ordering of the dipoles will lead to an increase in polarization. The position of the anomaly in the dielectric permittivity is due to the characteristic relaxation time of the considered subsystem.

The imaginary part of the dielectric permittivity is shown in fig. 5. In the temperature range (130–210) K, a sharp increase in the dielectric permittivity is observed. In the magnetic field H = 8 kOe, Re (ε (ω)) increases and the relative change in permittivity δε _H = (ε ( H , T ) – – ε (0, T) ) / ε (0, T )) reaches the maximum of 6 % at T = 184 K. A sharp decrease in permittivity with decreasing temperature is also described in the model of freezing of dipole moments with an activation energy Δ E = 800–1000 K.

As the concentration of gadolinium ions increases, the dispersion of inhomogeneous electronic states and local magnetic fields increases too. The temperature range of the dielectric losses increases for the composition with x = 0.2 (fig. 6), the temperatures of the maxima of the imaginary part of the dielectric permittivity practically do not shift in the magnetic field, and the dielectric loss increases (fig. 6). In a magnetic field, the dielectric permittivity increases more sharply (fig. 6), as a result of which the magneto-capacity changes its sign from a negative value 5–7 % to a positive 4–5 % in the temperature range 140–400 K (fig. 7).

The temperatures of the maxima of dielectric losses increase within one percent in a magnetic field and increase with increasing frequency. The relaxation frequency is described by the exponential dependence (1) with the activation energy Δ E = 0.035 eV. The dielectric losses are due to the scattering of hole type polarons.

Conclusion. For the composition Gd_0.04Mn_0.96S, a sharp abrupt decrease in the dielectric permittivity at low temperatures is found, which is associated with lattice structural distortion. As the concentration of gadolinium ions increases, the low-temperature maximum of the imaginary dielectric permittivity increases too and shifts to high temperatures, just as in a magnetic field. In solid solutions Gd x Mn 1– x Se, the magneto-capacitance effect was observed at temperatures several times higher than the Neel temperature, with a change in sign with respect to temperature. The logarithm of the relaxation frequency of dielectric losses exponentially increases with heating and depends on the magnetic field.

The decrease in dielectric losses in a magnetic field is caused by the redistribution of localized electrons by t2g, and by the shift in the energy of the electron density maximum relative to the chemical potential, which leads to an increase in the activation energy. These results are well described in the Debye model with the freezing of dipole moments. The increase in the dielectric permittivity above room temperature is caused by an increase in the electron delocalization radius and the disappearance of the orbital-charge ordering. Delocalization of electrons and the transition to the band type conductivity leads to a positive magneto-capacity as a result of Maxwell–Wagner effect.