Дифференциальная термоэдс двухслойных графеновых нанолент с адсорбированными атомами водорода

DOI:

Одним из важнейших параметров, определяющих термоэлектрические свойства вещества, является его дифференциальная термоЭДС, представляющая собой физическую величину, ха- рактеризующую скорость изменения индуцированной градиентом температуры разности потенциалов (ЭДС) при изменении температуры. Различие тепловых энергий электронов на концах нанолент вызывает дополнительный дрейф носителей тока от нагретого конца ленты к более холодному. Накопление носителей заряда на холодном конце ленты и дефицит их на нагретом вызывает появление термоЭДС. В настоящее время большое число публикаций посвящено исследованию термоэлектрических свойств низкоразмерных структур, таких как углеродные нанотрубки, графен [1; 8; 12; 17].

Разнообразие структурных модификаций графеновых нанолент является причиной достаточно широкого диапазона их термоэлектрических свойств [5]. Фиксирующиеся в полупроводниковых структурах явления локализации электронов могут приводить к зависимости транспортных коэффициентов от температуры и напряженности внешних электрического и магнитного полей, которые особенно сильно проявляются в области низких температур [1; 5; 8; 12; 17].

Многочисленные исследования показывают, что электрофизические свойства углеродных наноструктур (термоЭДС, электрическое сопротивление и др.) обладают высокой чувствительностью к составу газовой среды, окружающей наноструктуру [16]. С учетом этой особенности разрабатываются химические сенсоры газов на основе углеродных нанотрубок и графеновых лент [10]. Углеродные наноструктуры являются подходящим материалом для конструирования эффективных термоэлектрических преобразователей.

Из вышесказанного ясно, что исследование термоэлектрических свойств примесных двухслойных графеновых нанолент является актуальной и практически значимой задачей. Представленный аналитический метод расчета позволяет выявить зависимость коэффициента дифференциальной термоЭДС двухслойных графеновых лент от концентрации адсорбированных на их поверхности атомов водорода, напряженности внешнего постоянного электрического поля, геометрических размеров лент и величины поперечного электростатического потенциала между слоями ленты.

1. Математическая модель и эффективные уравнения

Аналитическая модель термоэлектрических характеристик двухслойных примесных графеновых лент строится в квазиклассическом приближении времени релаксации. Электронные свойства углеродных наноструктур описываются в π-электронном приближении Хюккеля внутри одной минизоны и не учитывают межзонных переходов. Закон дисперсии, описывающий электронные свойства однослойных графеновых лент без учета кулоновского взаимодействия электронов на одном узле [5], получен в рамках метода сильной связи:

E ( p ) = ±y 1 ± ± 4cos ( ap x ) cos ( ap y / 3 ) + 4cos² ( ap y /3 ) , (1)

где a = 3 b/ 2 Й ; b = 0,142 нм - характерное расстояние между соседними атомами углерода в графене; p = (p x , p y ) - двумерный импульс электронов; у » 2,7 эВ - интеграл перескока электронов между соседними узлами кристаллической решетки в графене [14].

Разные знаки в законе дисперсии относятся, соответственно, к зоне проводимости и к валентной зоне. Электронные свойства графена обладают сильной анизотропией.

Адсорбция атомов водорода на поверхности графеновых лент описывается в рамках периодической модели Андерсона. Так как геометрическая конфигурация лент определяет их термоэлектрические свойства, то использование предложенной модели вполне оправдано.

Периодическая модель Андерсона [6] рассматривает две группы электронов: коллективизированные s-электроны и локализованные d-электроны. Коллективизированные частицы считаются свободными, а локализованные – взаимодействуют между собой посредством кулоновского отталкивания на одном узле. Модель может успешно применяться и для исследования свойств низкоразмерных углеродных структур. Атом углерода в слое графена образует с ближайшими соседями 3 химические связи σ-типа. Четвертая p-орбиталь создает химическую связь π-типа, описывающую состояние коллективизированных электронов. В модели учитывается кинетическая энергия электронов графена и электронов атомов примеси, взаимодействующих посредством потенциала гибридизации. Энергия колебаний атомов решетки кристалла, энергия электронов внутренних оболочек атомов и электронов, участвующих в образовании химических связей σ-типа, в данной модели не рассматриваются [6].

Гамильтониан, описывающий состояние электронов кристалла, содержащего примеси, в приближении ближайших соседей и π-электронном приближении в рамках модели Андерсона имеет вид [6]:

H = УЛк (c +Tc а + c ++лc,„ ) + У £•ndrr + 52 Undndi + Д ja j+Дa     j+Дa ja          la la           11 lф j ,Д,а                                            l ,a                  I

+ У + d, + V*d+ c ) lj jσ lσ      lj lσ jσ l,j,σ где tД - интеграл перескока электронов между соседними узлами кристаллической решетки; U- константа кулоновского отталкивания электронов примеси; cja и c +a - ферми-операторы уничтожения и рождения электронов кристалла на узле j со спином о; dja и d a - ферми-операторы уничтожения и рождения электронов на примеси l со спином σ; nldσ – оператор числа электронов на примеси l со спином σ; εlσ – энергия электрона на примеси l со спином σ; Vlj – матричный элемент гибридизации состояний электронов примеси l и атома j кристалла.

После выполнения Фурье-преобразования по кристаллическим переменным гамильтониан Андерсона (2) принимает вид:

H = У £ (k Cc.„c. + У ^nd + У Undnd. + ) ka ka           la la k,σ                          l,σ

+У( Vlkc +„ d,„ + V, * d+ck „)

lk jσ lσ     lk lσ kσ l,k,σ где s(k) - зонная структура углеродных наночастиц в приближении Хюккеля; c^ и cka - Фурье-образы ферми-операторов рождения и уничтожения электронов в состоянии с волновым вектором k и спином σ; Vlk - матричный элемент гибридизации состояния электрона примеси l и состояния | ka) кристалла.

После использования метода функций Грина, переходя в k -пространство по кристаллическим переменным путем Фурье-преобразования операторов рождения и уничтожения электронов кристалла, зонная структура однослойных графеновых лент с адсорбированными атомами водорода может быть представлена в следующем виде [9]:

Ea ( k ) = 2

£k + £la

±[⁽ £ , — £ ,a ) ’ + ⁴ ^^ -I V I² ] ’

где N – число атомов углерода в решетке, определяющее размеры ленты; N_imp – число адсорбированных атомов водорода на поверхности ленты; V – потенциал гибридизации; ε _{l σ} = –5,72 эВ – энергия электрона примеси; ε _k – зонная структура идеальной однослойной графеновой ленты, определяемая дисперсионным соотношением (1).

Значение потенциала гибридизации, определяемое интегралом перекрывания волновых функций s -орбитали атома водорода и p_х -орбитали атома углерода, оценивается в рамках полуэмпи-рического метода MNDO: V = –1,43 эВ [10]. Энергия электрона примеси ε _{l σ} = –5,72 эВ оценивалась при помощи метода, описанного в работах [4]. Величина интеграла перескока t ₀ = 2,7 эВ взята из справочных данных [15].

Двухслойные примесные графеновые ленты состоят из двух гексагонально структурированных слоев углерода с адсорбированными на их поверхности атомами водорода, упакованных по типу ABAB. Система рассматривается в приближении Хюккеля в рамках метода сильной связи [11], в котором учитывается только энергия π-электронов в приближении ближайших сосе- дей, интеграл перескока между узлами гексагональной решетки равен 2,7 эВ, а между слоями графена – 0,4 эВ [13]. В рассматриваемой модели между слоями графена приложен электростатический потенциал U. Зонная структура, полученная в приближении сильной связи, позволяет записать закон дисперсии для двухслойных примесных графеновых лент в виде [13]:

E? (U ) = ± J E "(k) + Y ² /2 + U ⁴ /4 ± Y ⁴ /4 + ( Y ² + U ²) E >),              (5)

где дисперсионное соотношение однослойного графена ε _p определяется формулой (1).

Закон дисперсии двухслойных примесных графеновых лент является периодической функцией, и разлагается в ряд Фурье [2; 18]:

X л     ( mPxb )

^Ep^(U ) = L A ms cos I       | ,

m.s          V ^ / где b – характерное расстояние между соседними атомами углерода; Ams – коэффициенты разложения в ряд Фурье дисперсионного соотношения электронов, выражающиеся формулой (7):

π

Ams =± J Ep^ ( U ) cos( pb ) dp_x .

—n

В квазиклассическом приближении функция распределения электронов f_s ( p , r ), зависящая от их импульсов и координат, находится из кинетического уравнения Больцмана [7]. Уравнение Больцмана используется для изучения процессов теплопереноса и переноса электрического заряда в системах, где взаимодействие между частицами считается малым параметром. В силу того, что в наноструктурах при низких температурах порядка 40 K время релаксации является практически постоянной величиной и почти не зависит от изменения температуры [14], интеграл столкновений можно выбрать в приближении времени релаксации ( т -приближении).

Кинетическое уравнение Больцмана в приближении постоянного времени релаксации записывается в известном виде [7]:

^d f s ⁽ P , ^{r )} , _F^d f s ⁽ P , ^{r )    f}s ⁽ P , ^{r )} — f 0 s ⁽ P , ^{r )}

+ F= dt         dp             т где fs(p, r) – функция распределения электронов, зависящая от импульса и координат; f0s(p, r) – равновесная функция распределения Ферми; F – действующая на электрон электростатическая сила.

Аналитическое выражение для коэффициента дифференциальной термоЭДС получено с использованием расчетной методики, описанной в работе [3]. С учетом того что функция f_s ( p , r ) должна удовлетворять уравнению непрерывности, запишем уравнение Больцмана в приближении времени релаксации в операторной форме:

L^_Pf s + div ( ^Л ) = f ⁰^ ^^^),

где оператор выражается соотношением:

' _ d p d + 1 ^p dt d p т

Плотность тока можно вычислить по формуле:

j ( r ) = e У V . ( p ) f_s ( p , r ) .                                      (11)

p , s

В стационарном случае при отсутствии источников зарядов дивергенция плотности тока равна нулю div j ( r ) = 0, и решение уравнения (8) будет иметь вид:

- 1

где L_p – обратный оператор.

f ⁽⁰⁾ ( p , r ) = L p

' f)s (p,r ) )

I T J.

С учетом того что концентрация электронов проводимости n = const считается постоянной в линейном приближении по величине градиента температуры V _xT , получено аналитическое соотношение для дифференциальной термоЭДС двухслойных примесных графеновых нанолент во внешнем постоянном электрическом поле:

V Г df v a          ' E 2( m 2 + m'2) +1

• ⁵ ( ^E ) = У\^У A ms m У A m m 1

S _— Г ^d T m         m ‘

*

K ( E, m, m')

*[ EmR (E, m, m , px ) + M (E, m, m', px)] +

E3 (m '3 — 2 m2 m') + Em'

K ( E, m, m')

+--Г--У J f У J f У Amsm У Amm ’

ZJ d- Г "-Г d” s —Г

T (E, m, m , Px )} dpx +

• ¹----- F ⁽ E , m , m ' , Px ,, Px . ) dPx , dPx. .       ⁽¹³⁾

P ( E , m , m )

Здесь введены следующие обозначения:

K ( E , m , m' ) = [ E ⁴( m ⁴ + m' ⁴ — 2 m ² m' ²) + 2 E ²( m ² + m' ²) + 1 ][ E ² m ² + 1 ] , P ( E , m , m ') = [ E ² m ² + 1 ] [ E ² m ' ² + 1 ], R ( m , m' , p_x ) = cos( mp_x )sin( mp x ) ) + cos( mp_x )cos( mp x ) ) — sin( mp_x )sin( mp x ) ) , M ( m , m' , p_x ) = sin( mp_x )sin( m 'P) ) + sin( mp_x )cos( m 'P) ) + cos( mp_x )sin( mp x ) ), T ( E , m , m' , P_x ) = [ cos( mP_x )cos( mP x ) ) — Em sin( mP_x )cos( mP x ) ) ] ,

F ( E , m , m ' , p _x ) = [ sin( m P)_x ) + Em cos( m P>_x ) ] * * [ sin( mp_x ) + 2 Em cos( mp_x ) — E ² m ² sin( mp_x ) ] , где A_ms и A_{m ′ s} – коэффициенты разложения энергии электронов двухслойных примесных графеновых лент в ряд Фурье; f – функция распределения Ферми – Дирака; Т – абсолютная температура.

2. Результаты численного анализа

Представлены результаты численных расчетов зависимости дифференциальной термоЭДС двухслойных графеновых нанолент с адсорбированными атомами водорода от напряженности внешнего постоянного электрического поля. Для удобства качественной оценки и наглядной визуализации дифференциальная термоЭДС выражается в относительных безразмерных единицах.

Значение относительной единицы измерения дифференциальной термоЭДС, отложенной по оси у , равно 3,1 В/К.

Численный анализ зависимости коэффициента дифференциальной термоЭДС двухслойных примесных графеновых нанолент от амплитуды внешнего постоянного электрического поля проведен на примере лент (10,0)-типа. Изменение дифференциальной термоЭДС при адсорбции двухслойными графеновыми лентами типа (10,0) одного атома водорода показано на рисунке 1. Двухслойная лента с одним атомом примеси имеет коэффициент термоЭДС приблизительно на 0,01 мкВ/К ниже, чем аналогичная бездефектная лента. Снижение дифференциальной термоЭДС при адсорбции двухслойными лентами атомов водорода обусловлено, как и для других транспортных коэффициентов [18] (коэффициент диффузии электронов, удельная электропроводность) тем, что электроны, оказавшиеся в локализованном состоянии, не участвуют в переносе заряда и не дают вклада в термоЭДС.

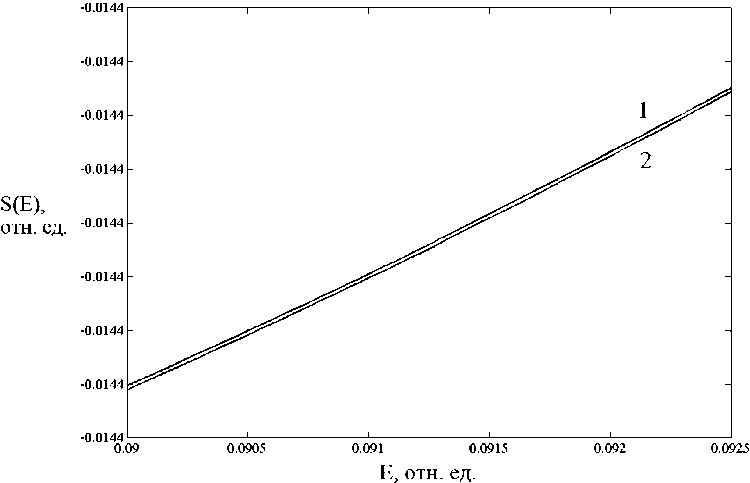
Рис. 1. Зависимости дифференциальной термоЭДС S ( E ) от величины напряженности E внешнего электрического поля: для двухслойных графеновых лент типа (10,0):

1 – идеальных; 2 – с адатомом водорода

Уменьшение дифференциальной термоЭДС двухслойных графеновых нанолент пропорционально концентрации адсорбированных на их поверхности атомов водорода, то есть количеству образовавшихся локализованных адсорбционных связей, что наглядно видно из рисунка 2. Графики зависимостей, представленные на рисунке 2, построены с учетом фиксированного значения электростатического потенциала между слоями ленты, равного U = 1 B.

Для двухслойных примесных нанолент построены зависимости дифференциальной термоЭДС от напряженности внешнего постоянного электрического поля при различных значениях электростатического потенциала между слоями ленты типа (10,0), показанные на рисунке 3. При возрастании напряжения между слоями ленты от 0 до 2,2 В происходит рост дифференциальной термоЭДС по абсолютной величине, а при дальнейшем увеличении потенциала происходит ее снижение, что объясняется, как и для беспримесных двухслойных графеновых нанолент, перестройкой собственного электронного спектра под воздействием внешнего постоянного электрического поля. Дифференциальная термоЭДС двухслойных примесных графеновых лент нелинейно зависит от амплитуды внешнего электрического поля. Отрицательный знак дифференциальной термоЭДС указывает на электронный характер электропроводности в двухслойных примесных графеновых нанолентах. Следует отметить, что подобное поведение термоЭДС зафиксировано и для однослойных и двухслойных бездефектных и примесных графеновых нанолент.

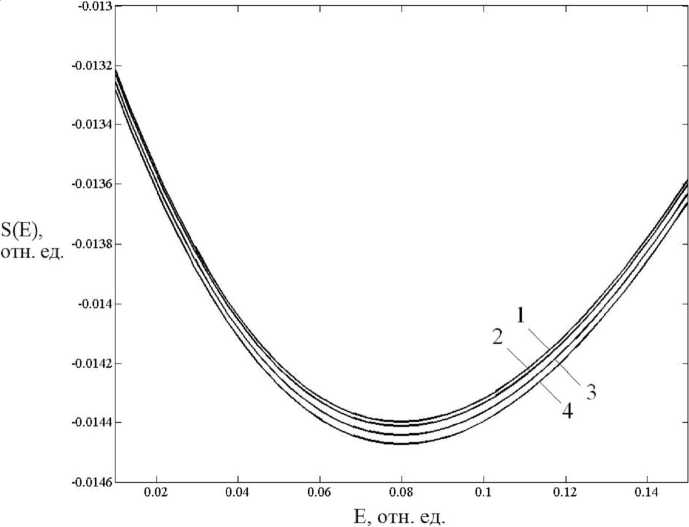
Рис. 2. Зависимости дифференциальной термоЭДС S ( E ) от величины напряженности E внешнего электрического поля для двухслойных примесных графеновых лент типа (10,0):

1 – один адатом водорода; 2 – 100 адатомов; 3 – 300 адатомов; 4 – 500 адатомов

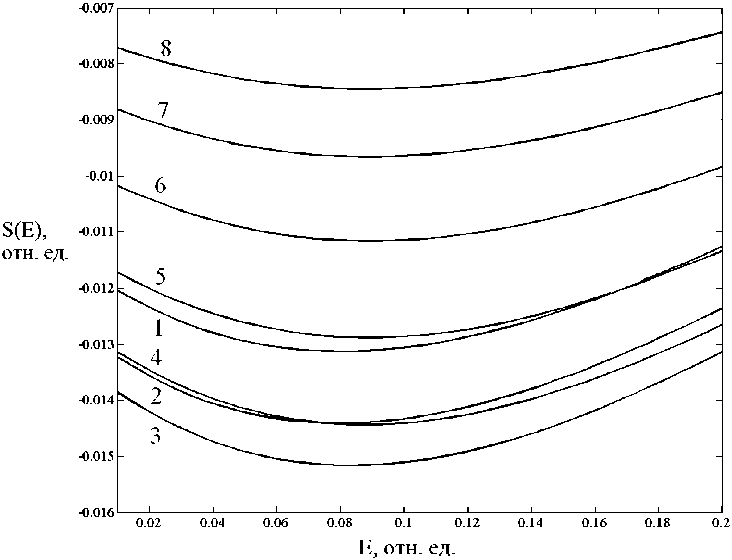
Рис. 3. Зависимости дифференциальной термоЭДС S ( E ) от величины напряженности E внешнего электрического поля для двухслойных примесных графеновых лент типа (10,0) со 100 адатомами водорода для различных значений электростатического потенциала между слоями графена:

1 – для U = 0 В; 2 – для U = 1 В; 3 – для U = 2 В; 4 – для U = 3 В; 5 – для U = 4 В;

6 – для U = 5 В; 7 – для U = 6 В; 8 – для U = 7 В

Широкие двухслойные ленты обладают большими по абсолютной величине значениями дифференциальной термоЭДС (рис. 4), что явно связано с большей концентрацией электронов, участвующих в транспорте электрического тока по поверхности ленты.

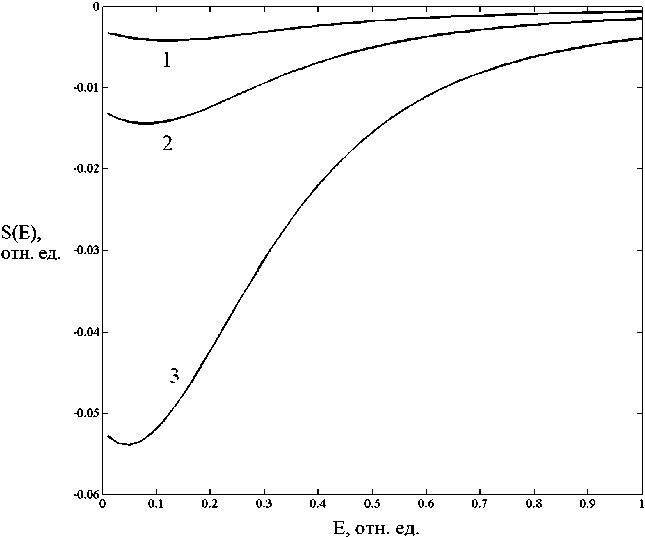
Рис. 4. Зависимости дифференциальной термоЭДС двухслойных примесных графеновых лент различной ширины ( n , 0) для фиксированных значений электростатического потенциала между слоями ленты U = 1 В и числа адсорбированных атомов водорода N_imp = 100 от амплитуды внешнего постоянного электрического поля:

1 – для n = 5; 2 – для n = 10; 3 – для n = 20

Согласно данным численных расчетов при напряженности внешнего электрического поля Е = 2,32 ∙ 10⁵ В/м, Т = 300 К, дифференциальная термоЭДС двухслойной примесной ленты (5,0)-типа с N_imp = 100 адатомами водорода равна 12,6 мкВ/К, а ленты (10,0)-типа с тем же числом адатомов – 39,3 мкВ/К.

Заключение

Сформулируем кратко основные результаты проведенного исследования и выводы:

• 1.    Получено аналитическое соотношение для коэффициента дифференциальной термоЭДС двухслойных графеновых лент с адсорбированными атомами водорода в квазиклассическом приближении времени релаксации во внешнем постоянном электрическом поле.

• 2.    Дифференциальная термоЭДС примесных двухслойных графеновых нанолент нелинейно и немонотонно зависит от напряженности внешнего постоянного электрического поля, а в сильном поле для всех рассмотренных типов лент стремится к постоянному значению.

• 3.    Дифференциальная термоЭДС графеновых лент имеет знак минус вследствие того, что носителями зарядов в углеродных наночастицах являются отрицательно заряженные электроны.

• 4.    Показано, что с ростом ширины графеновых лент их дифференциальная термоЭДС возрастает по абсолютной величине, что объясняется увеличением числа квантовых состояний электронов в зоне проводимости.

• 5.    Увеличение электростатического потенциала между слоями ленты до 2,2 В приводит к росту абсолютных значений дифференциальной термоЭДС двухслойных графеновых лент с адсорбированными атомами водорода. Дальнейшее увеличение поперечного напряжения между

• 6.    Адсорбция малых концентраций атомарного водорода незначительно снижает по абсолютной величине дифференциальную термоЭДС двухслойных графеновых нанолент, качественно не изменяя характера ее зависимости от напряженности внешнего постоянного электрического поля.

слоями ленты снижает термоЭДС по абсолютной величине, что обусловлено собственной динамикой электронов проводимости, а также ограниченностью и периодичностью дисперсионных соотношений примесных двухслойных графеновых нанолент.

ПРИМЕЧАНИЕ

• ¹    Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 14-02-31801).