Дифференциальное уравнение движения частицы зернового материала в сепарирующем зернометателе

С каждым годом по всей стране увеличивается валовой сбор зерновых культур. В связи с этим растет потребность в современных, многофункциональных зерноочистительных машинах, способных удовлетворить потребности фермерских хозяйств.

В полной мере удовлетворяет возрастающим требованиям сепарирующий зерномета-тель [1]. Зернометатель способен выполнить очистку зернового материала в барабане устройства, его сушку и фракционирование при метании зерна в воздушный поток.

Для определения основных технологических параметров сепарирующего зерномета-теля были проведены теоретические исследования. Представлено аналитическое описание движения зернового материала [2], где вывели дифференциальное уравнение второго порядка, которое является линейным неоднородным с постоянными коэффициентами, описывающее перемещения зерна в сепарирующем зернометателе.

Аналитическое описание движения зернового материала

Рассмотрим движение частиц зернового материала по очистительному устройству сепарирующего зернометателя. Движение частиц по очистительному устройству обусловлено действием сил со стороны очистительного устройства и гравитационной силы (рис.) [2]. Очистительные устройства установлены во вращающемся барабане зернометателя.

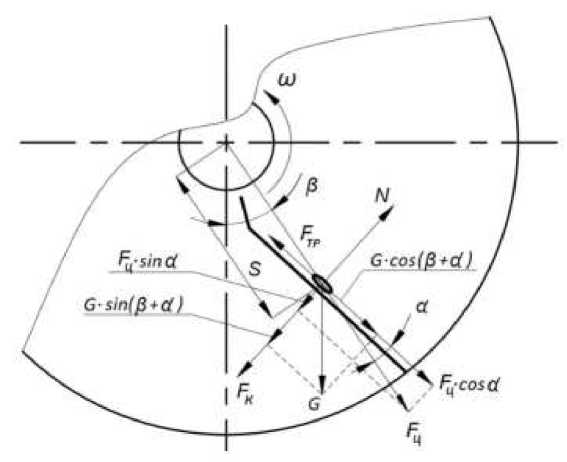
Рисунок - Схема сил, действующих на зерно во вращающемся барабане

Дифференциальное уравнение движения зернового материала согласно схеме сил, действующих на зерно во вращающемся барабане (рис. 1) имеет следующий вид:

d2S

т-^- = Р ц cos а — Р тр + G sin(p + а), где F_T p = fN - сила трения, Н; f- коэффициент трения зерна по очистительному устройству; Р_к = 2то ^| - сила центробежная, Н; m - масса зерна, кг; го - угловая скорость лопатки, рад/с; N- сила реакции опоры, Н; G = тд - сила гравитационная, Н; Р_ц = mSro² - сила центробежная, Н; S - расстояние от центра барабана до частицы зернового материала, м; а- угол наклона очистительного устройства, рад; p - угол положения частицы зернового материала, рад.

Ранее аналитически было получено выражение [2]:

—— + 2f — — S(cosа — f sin а) = Д?(<со5(В + а) — f sin(B + а)). dp2     dp                     о2

Получили дифференциальное уравнение второго порядка, которое является линейным неоднородным с постоянными коэффициентами.

Решение неоднородного линейного уравнения второго порядка

Решение дифференциального уравнения (1), как известно, состоит из общей части и частного решения.

Общее решение линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами имеет вид:

S = S 0 +S 4 ,                                 (2)

где S0 - общее решение однородного уравнения; S4 - частное решение.

Общее решение S0 зависит от значения корней характеристического уравнения 2. Для составления характеристического уравнения неизвестную величину заменяют единицей, ее производные - соответствующими степенями корней 2, сохраняют все коэффициенты и отбрасывают правую часть.

Найдем сначала общее решение однородного уравнения:

-—т + 2f— — S(cosa — f sina) = 0.

ар2dp

Применительно к уравнению (3) характеристическое уравнение примет вид:

22 + 2f2 — (cos a — f sin а) = 0 .

Квадратное уравнение (3) имеет два корня:

2 1 = — f + ^f² + (cos a — f sin a) ,

22 = — f — ^f2 + (cos a — f sin a).(5)

Исследование выражений (5) показало, что при f = 0.1.. .0.4 и а = 0 ... 50о получим положительную величину под корнем. Поскольку характеристическое уравнение имеет решение, а корни являются действительными числами и различны, то общее решение однородного уравнения будет следующим:

S₀ = c-^^ + c₂e ^²^ ,                                (6)

где c 1 , c₂ находятся по начальным условиям.

Частное решение неоднородного уравнения зависит от правой части уравнения (1) и корней характеристического уравнения (4). Частное решение ищем в виде:

F(P) = е«ДР п (Р) • cos^bg) + Q m (P) • sin(bp)],                   (7)

где к, b - заданные постоянные; Р_п(Р), Q_m(P') — многочлены степени п и т соответственно.

Представим правую часть уравнения (1) и методами преобразования тригонометрических выражений приведем уравнение к требуемому виду (7).

F(P) = 99 (cos(p + a) — f sin(P + a))

to2

или

F(P) = —- (cos a — f sin a) • cos Р--- (sin a + f cos a) • sin Р(8)

to2to или

F(P) = e0^ [-9- (cos a — f sin a) • cos(1 Р) —9_ (sin a + f cos a) • sin(1 p)]. to2to

Из уравнений (7) и (8) находим постоянные и многочлены: к = 0, b = 1,

Рп(Р') = 99 (cos a — f sin a-),       Qm(P) = — 99 (sin a + f cos a-), т. е. Рп(Р) и Qm(P) - многочлены нулевой степени.

Поскольку число к + bi = 0 + 1i = 1i не является корнем характеристического уравнения (4), то частное решение линейного неоднородного дифференциального уравнения второго порядка будет в виде:

S₄ = A cos Р + В sin Р .                             (9)

Для нахождения коэффициентов A и B необходимо значение соответствующих производных уравнения (9) подставить в уравнение (1).

Производные:                   Соответствующие коэффициенты:

S₄ = A cos р + В sin. р                       — (cos а — f sin а)

S 4’ = — A sin р + В cos р                             2f

S 4' = — A cos р — В sin р                              1

Получим уравнение из сумм произведений производных с соответствующими коэффи- циентами:

—A cos р — В sin р — 2f A sin р + 2f В cos р —

—A cos р (cos а — f sin а) — В sin р (cos а — f sin а) = = — (cos а — f sin а) • cos р--- (sin а + f cos а) • sin р .

Затем получим систему уравнений, приравнивая коэффициенты при sin р и cos р :

( В + 2fA + В(cos а — f sin а) = Ar(snia + f cos а); ш²

— A + 2fВ — A(cos а — f sin а) = A? (cos а — f sin а) ш²

Решив систему уравнений (11), найдем коэффициенты A и B :

g f2 sin(а')2 — 2f2 cos а —2f cos а sin а —3f sin а + cos(а)2 + cos а ш2 f2 sin(а')2■ + 4f2 — 2f cos а sin а —2f sin а + cos(а)2 + 2 cos а + 1' g  fcos(а')2 — 2f2 sin а —f2 cos а sin а +3f cos а —f sin(а')2 + cos а sin а + sin а ш2      f2 sin(а')2 + 4f2 — 2f cos а sin а —2f sin а + cos(а)2 + 2 cos а + 1

Представим общее решение дифференциального уравнения (1) в виде:

S = S₀ + S₄ = c^e^ + c₂e^x 2 ^ + A cos р + В sin р .                (14)

Величины постоянных коэффициентов c 1 и c₂ определяем из начальных условий. Для чего находим производную уравнения (14) и получаем переносную скорость:

aS

^U e =^ ар

AS поскольку ар = ш • а^и— =

= c₁Л₁e^{Л 1}^ + c₂Z₂e^z 2^ — A sinр + В cos р, dS

, получим:

— = ш(c₁2₁e^{Л 1}^ + c₂2₂e ^²^ — A sin р + В cos р) .

Примем следующие начальные условия р = р₀, S = S₀, U = U₀ , тогда получим:

S₀ = c₁e ^¹^⁰ + c₂e ^²^⁰ + A cos р₀ + В sinр₀ .

U₀ = ш(c₁Л₁e^{X 1}^^, + c₂Z₂e^z 2^° — A sin р₀ + В cos р 0 ) .

Решим систему из двух уравнений (17, 18) и найдем искомые коэффициенты c 1 и c₂ :

1   U₀ — ш2₂S₀ + A(ш sin р₀ + шХ₂ cos р 0 ) — В(ш cos р₀ — шЛ₂ sin р 0 )

e ^ i P °                              шХ 1 — шЛ₂

U₀ — шЛ₁S₀ + A(ш sin р₀ + шЛ 1 cos р 0 ) — В(ш cos р₀ — шЛ 1 sin р 0 ) шe^{Л 2}^° (Л₁ — Л₂)                             .

Найденные значения постоянных коэффициентов c 1 и c₂ подставим в уравнение (14) и получим следующее выражение:

1   U₀ — шЛ₂S₀ + A(ш sin р₀ + шЛ₂ cos р 0 ) — В(ш cos р₀ — шЛ₂ sin р₀

e ^i^ °                           шЛ 1 — шЛ₂

)-.е^-

U₀ — шЛ₁S₀ + A(ш sin р₀ + шЛ 1 cos р₀) — В(ш cos р₀ — шЛ 1 sin р 0 ) шe^{Л 2}^ ° (Л₁ — Л 2 )

e ^ 2 P +

+A cos р + В sinр.

Коэффициенты A и В подставим в уравнение (20) и получим искомое решение дифференциального уравнения (1):

g ' 1 ^р о

^U o — ^toA 2 ^S o +^|— ”7

f² sin(a)²-2f² cos a -2 f cos a sin a-3f sin a+ f² sin(a)² +4f² -2f cos a sin a-2f sin a+

+ cos(a)2+cosa

+ cos(a)²+2 cos a+1

] • (to sinpo + to^2 cos Po) — [-^2 •

fcos(a)² -2f² sin a -f² sin(a)²+4f²-

toAi — to^2

-f² cos a sin a +3f cos a-f sin(a) ² +cos a sina+sina-.  ,       „      з ■ о \

-2f cos a sin a-2f sin a+cos(a^ ² +2 cos a+1          COS p₀ to 2Sinp°)    ^^

Uo — toX1So + | — -g

f² sin(a)²-2f² cosa-2f cos a sin a-3f sin a+cos(a)²+cos a f² sin(a)²+4f²-2f cos a sin a -2f sin a+cos(a)²+2 cos a+1 .

]•

g

to2

,       „      ,       „ x r g fcos(a)2-2f2 sin a-f2 cos a sin a +3f cos a -

• ^(tosi ^ ^p o ^{+ to}A i ^cosp o )^— [ ^2 ^    . . .... . .4. .   .................. ..

toe'2Po(A1 — A2)

-fsin(a)2+cos a sina+sina-,  ,        „       ,   .  „ x

+ cos(a)2+2cos«+1   ] ^ (tocosP0 — toAs'np)

--g'2 —

f2 sin(a)2 — 2f2 cos a —2f cos a sin a —3f sin a + cos(a)2 + cos a f2 sin(a)2 + 4f2 — 2f cos a sin a —2f sin a + cos(a)2 + 2 cos a + 1

• cos P + -g • to²

fcos(a)2 — 2f2 sin a —f2 cos a sin a +3f cos a —f sin(a)2 + cos a sin a + sin a f2 sin(a)2 + 4f2 — 2f cos a sin a —2f sin a + cos(a)2 + 2 cos a + 1

sinp.

Подставим коэффициенты c 1 и c₂ в выражение (15) и получим уравнение переносной

скорости:

_  1

Ue = е^

Uo — toA2S0 + ^(to sin p0 + to^2 cos p0) — B(to cos p0 — toA2 sin P0) toAl — to^2

•A1e'ip

—

Uo — toA1S0 + A(to sin p0 + toA1 cos P0) — B(to cos p0 — toA1 sin P0) toe'2Po(A1 — A2)

A₂e ' 2 ^p —

— A sin p + В cos p.

Полученное уравнение (21) представляет собой уравнение перемещения частицы сыпучего материала во вращающемся барабане сепарирующего зернометателя и показывает изменение расстояния от центра вращения барабана до зерна. Уравнение (22) позволяет определить переносную скорость движения зерна.

Выводы

Решением дифференциального уравнения второго порядка, которое является линейным неоднородным с постоянными коэффициентами (1), являются выражения (21) и (22). Дальнейший анализ выражений позволит определить траектории и скорости перемещения зернового материала в зависимости от начальных условий и других переменных. Полученные результаты теоретических исследований позволят определить оптимальные кинематические, геометрические и конструктивные параметры сепарирующего зернометателя для создания экспериментального устройства.