Дифференциальные характеристики к радиусному участку профиля зубьев червячной фрезы для нарезания шлицевых валов

Обработка шлицевых валов червячными фрезами относится к многофункциональному и многопараметрическому процессу. Формирование профиля шлицев производится при относительном движении заготовки и фрезы, происходящем в объеме. Расчет сил при такой обработке требует моделирования всего технологического процесса в целом и в частности червячной фрезы, также в объеме и в разных пространственных положениях. В связи с этим в работе [1] была предложена модель червячной шлицевой фрезы, описанная векторными функциями.

На основе описания фрезы рассматриваются дифференциальные характеристики (касательная, нормаль, бинормаль) в точке радиусного участка фрагмента профиля фрезы. Дифференциальные характеристики получены с учетом винтового профиля стружечных канавок. Дифференциальные характеристики в процессе вращения фрезы и в процессе обработки также изменяют пространственное положение, что позволяет учесть изменяющиеся значения сил.

Весь зуб состоит из пяти режущих лезвий, два из которых имеют радиусный профиль. Каждое режущее лезвие представляется соответствующим вектором. Радиусный участок описывается векторной функцией дуги окружности. В качестве общей (глобальной) системы координат выбрана точка в начале одного из векторов прямолинейной режущей кромки.

Фреза рассматривается как набор векторных функций, которые записаны в одной (глобальной) системе координат уравнением:

r r = r i + M • r i ,                                         (1)

где r_i – вектор, записанный в своей (локальной) системе координат;

M – матрица перехода;

r_oi – вектор переноса локальной системы координат в глобальную систему.

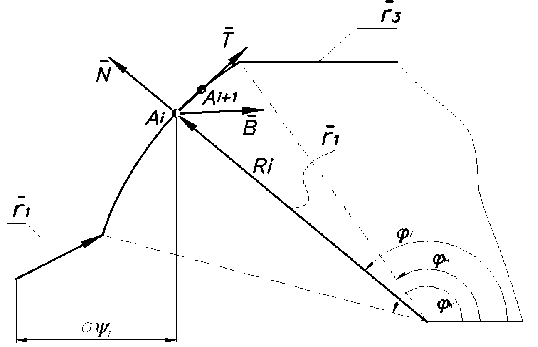
Фрагмент зуба червячной фрезы для нарезания шлицевых валов

На рисунке изображен фрагмент профиля зуба червячной фрезы для нарезания шлицевых валов в нормальном сечении. Нахождение точек координат при моделировании не представляет труда, если двигаться по векторам или по радиусным участкам векторных функций. Координаты аналогичных точек на соседних зубьях этой же рейки находятся путем параллельных переносов. Однако на реальной фрезе точки всех зубьев расположены по винтовой. Другими словами, координаты точек всех зубьев следует рассчитывать с учетом винтового закручивания. Для этого необходимо вычислить координаты по винту каждой точки с учетом движения по оси фрезы.

Модель, которая описывает режущие лезвия всей шлицевой фрезы, является по терминологии, принятой в САПР, проволочной моделью. Поскольку фреза рассматривается в пространстве, то принятая модель позволяет находить точки, принадлежащие режущим лезвиям, которые производят или не производят снятие металла в процессе обработки. Это, в свою очередь, дает возможность определять силы, действующие на определенный участок режущего лезвия. Силы, действующие на дифференциально малый участок режущего лезвия фрезы, зависят от многих факторов. Основными факторами являются прочностные и теплофизические свойства обрабатываемого материала. Силы, как известно, при фрезеровании зависят от толщины срезаемого в данный момент времени материала. Сама толщина срезаемого слоя зависит от положения точки, принадлежащей режущему лезвию фрезы в пространстве и соответственно от проекций силы резания, действующей в данный момент на режущий клин на оси координат станка.

Силу резания при фрезеровании раскладывают на 3 составляющие: касательная T , нормаль N , бинормали B (рисунок).

Если рассматривать радиусный участок фрезы для обработки шлицевых валов, который имеет пространственное положение, то в дифференциально малой окрестности касательную можно представить как хорду, соединяющую соседние точки.

Модуль касательной, проходящей через точки и с учетом винтового движения, рассчитывается как:

IT\ = \(xi+1 - xi )2 + (yi+1 - yi )2 + (zi+1 - zi )2 .

Проекции единичных векторов касательной T_i на оси OX, OY, OZ:

ex (T) =      .,(3)

e- T = + T,(4)

ez (Ti) = Zi+T—Z".(5)

Нормаль по направлению совпадает с вектором r1 . Поэтому модуль нормали определя- ется как:

| ^ | = 7⁽ xi — x 0 ) 2 ^{+ (} yi — y 0 ) 2 ^{+ (} z i — ^Z 0 ) 2 .

Проекции единичных векторов касательной N на оси OX, OY, OZ:

e x ( N ) =

xi

- x o

N

e y ( N ) =

y i ^- У o

N

ez(N) = zN0 .

Бинормаль определяется как векторное произведение касательной и нормали:

B = T • N • sin 6.(10)

Аналогично определяются единичные векторы бинормали.

Угол 6 между касательной и нормалью вычисляется из выражения cos6 = ex(Ti) • ex(Ni) + e^(T) • ey(N) + ez(T) • ez(Nv).(11)

Таким образом, найденные дифференциальные характеристики, привязанные к глобальной системе координат станка, позволяют вычислять проекции сил резания на оси координат в разных положениях фрезы и на разных зубьях и вычислять суммирующее их воздействие.