Дифференциальные определяющие уравнения сред, работающих в условиях конечных деформаций

A method is proposed for constructing of constitutive equations system for description of mechanical behaviour of the media with non-linear dissipative properties undergoing finite deformation. For this purpose the scheme of mechanical behaviour of the material is used. This scheme consists of combination of horizontally placed elastic, viscous and plastic elements. The mechanical properties of model elements are described by the appropriate well known equations of non-linear elasticity theory, the theory of flow of non-linear viscous liquids and the theory of plastic flow of material under finite deformation of continuum. It is shown that the dissipative inequality fulfils automatically in this method.

Для моделирования вязкоупругого поведения и вязкотекучих свойств конечнодеформируемых материалов используются модели интегрального и дифференциального типа. В моделях интегрального типа история деформирования среды учитывается с помощью интегральных уравнений. Их трудно обобщить на более сложные ситуации (например, для моделирования процессов массобмена в диссипативной среде, которые в технологии изготовления полимерных материалов играют основную роль). Попытка учета повреждаемости и тиксотропности эластомерных материалов в интегральных моделях делает их сложными для практического применения. Более привлекательным, по мнению автора, является путь построения дифференциальных феноменологических моделей. Они более просты и удобны для расчетов и для идентификации констант по имеющимся экспериментальным данным, позволяют с хорошей точностью описать реальные механические свойства материала. Этим, по-видимому, объясняется интерес в последние годы к дифференциальным моделям сплошной среды, работающей в условиях конечных деформаций.

В дифференциальных моделях для описания реологических свойств материала чаще всего используются тензорные внутренние переменные. Как правило, им приписывается физический смысл напряжений [1–5] или деформаций [6–12]. Математические модели такого типа удобно иллюстрировать с помощью символьных схем механического поведения среды. Однако в опубликованных работах не рассматривается общая теория построения моделей дифференциального типа с произвольным видом соединения элементов для сред, работающих в условиях конечных деформаций. Их нельзя получить простым обобщением моделей, применяемых для сред с малыми деформациями. Связано это с тем, что полная мера деформации не может быть представлена суммой мер деформации элементов схемы. В уравнениях эволюции внутренних переменных должны использоваться объективные производные, выбор которых требует соответствующего обоснования.

Реологические модели (имеющие простую символьную интерпретацию в виде схем Максвелла, Кельвина – Фойгта, Пойтинга – Томпсона и т. д.) сформулированы в работе [13]. Термодинамическая состоятельность простых определяющих уравнений

Общие вопросы неравновесной термодинамики обсуждается в статьях [14,15]. Наибольший интерес, по мнению автора, представляют идеи, сформулированные в статье [16]. В данной работе использован близкий подход, основанный на аддитивном разложении тензора скоростей деформирования среды.

Ниже предлагается простой метод получения определяющих уравнений, построенный на использовании символьных схем. Его достоинствами являются физическая прозрачность каждого из используемых математических выражений, удобство построения математической модели среды, отсутствие в определяющих уравнениях объективных производных от тензоров напряжений. Большой выбор способа соединения элементов на схеме дает дополнительные возможности для разработки модели, сочетающей точное описание поведения среды с содержанием минимального числа внутренних переменных.

Использование схемы механического поведения среды для построения системы определяющих уравнений

Для построения системы определяющих уравнений сложных сред предлагается использовать схему механического поведения материала. Один из возможных примеров такой схемы показан на рисунке. При выборе математической модели материала должны выполняться следующие правила:

• 1)    схема механического поведения среды должна состоять из точек, соединенных упругими, вязкими и пластическими элементами;

• 2)    все элементы на схеме должны располагатьсяся горизонтально. В результате можно говорить о левой и правой точках соответствующих элементов;

• 3)    элементы соединяются с точками на схеме с левой или правой стороны и не могут соединяться с точками сверху или снизу;

• 4)    каждой точке на схеме ставятся в соответствие тензор скоростей деформации этой точки, который играет роль тензорного параметра, необходимого для построения математической модели;

• 5)    каждому элементу на схеме ставится в соответствие тензор напряжений Коши и тензор скоростей деформации этого элемента.

Особенностью рассматриваемого подхода является то, что мы не используем понятия деформационных градиентов для внутренних точек на схеме механического поведения среды. Поэтому в данном подходе нельзя говорить о мультипликативном разложении деформационного градиента материала на произведение деформационных градиентов элементов схемы.

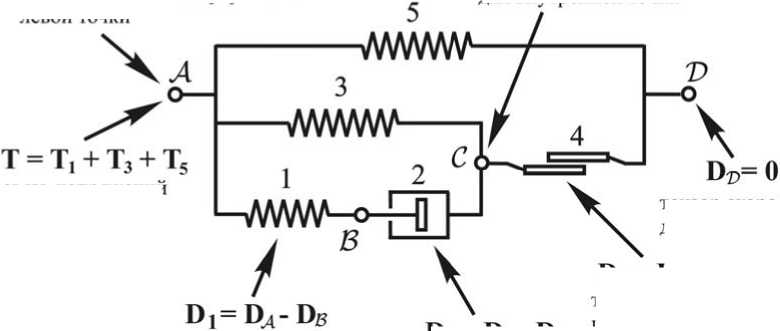
В приведенном примере (см. рисунок) схема механического поведения среды состоит из точек A , B , C , D , соединенных упругими элементами с номерами 1, 3 и 5, вязким элементом с номером 2 и пластическим с номером 4. Каждой точке на схеме мы ставим в соответствие тензоры скоростей деформирования D _A , D _B , D _C и D _D . Они используются для вычисления тензоров скоростей деформирования упругих элементов D ₁ , D ₃ и D ₅ , вязкого D ₂ и пластического D ₄ элементов. Особая роль на схеме механического поведения среды отводится ее левой A и правой B точкам. Алгоритм получения системы определяющих уравнений сводится к использованию правил, которые приводятся ниже.

Положение 1. Тензор скоростей деформации левой точки схемы совпадает с тензором скоростей деформации среды D , а тензор скоростей деформации правой точки схемы равен нулю.

Общие вопросы неравновесной термодинамики

Положение 2. Тензор скоростей деформации упругих, вязких и пластических элементов вычисляется как разность между тензорами скоростей деформации левых и правых точек этих элементов.

связь напряжений для внутренней точки

Цд= D тензор скоростей деформации левой точки

связь напряжений в левой точке тензор скоростей деформации упругого элемента тензор скоростей деформации вязкого элемента

D4 = Dc - Dp тензор скоростей деформации пластического элемента

D₂ d_b- d_c

тензор скоростей деформации правой точки

Рис. Одна из возможных схем механического поведения материала

В рассматриваемом примере эти утверждения означают, что при построении математической модели мы должны использовать равенства

D A = D , и D D = 0

для левой и правой точек на схеме,

D i = D a - D в , D 3 = D a - D с , D 5 = D a - D d           (1)

для упругих элементов и

D 2 = D в - D с , D 4 = D с - D d                         (2)

для вязкого и пластического элементов.

Следующим шагом является формулировка условий согласования тензоров напряжений. Как уже отмечалось, каждому из элементов на схеме механического поведения среды ставится в соответствие тензор напряжений Коши. В рассматриваемом примере (см. рисунок) это тензоры напряжений Коши упругих T ₁ , T ₃ и T ₅ , вязкого T ₂ и пластического T ₄ элементов.

Положение 3. Тензор напряжений Коши среды T равен сумме тензоров напряжений Коши элементов, соединенных с левой точкой схемы.

Положение 4. Сумма тензоров напряжений Коши элементов, соединенных слева с любой из внутренних точек схемы, равна сумме тензоров напряжений Коши элементов, соединенных с этой точкой справа.

В рассматриваемом примере (см. рисунок) тензор напряжений Коши материала равен сумме тензоров напряжений Коши упругих элементов,

T = T i + T 3 + t ₅ .                                           (3)

Для внутренних точек B и C справедливы равенства

T i = T 2 , T 2 + T 3 = T 4 .                                      (4)

Общие вопросы неравновесной термодинамики

Механические свойства упругих элементов

Для описания механического поведения элементов на схеме предлагается использовать хорошо известные уравнения механики нелинейного деформируемого тела или нелинейной жидкости. Так, для вычисления тензоров напряжений Коши в упругих элементах предлагается использовать массовую плотность свободной энергии.

Положение 5. Массовая плотность свободной энергии среды является функцией температуры и кратностей удлинения упругих элеиентов f = f (0,..., x 1, x 2, x 3,.), где θ – температура, λi1 , λi2 , λi3 – кратности удлинения i-го упругого элемента.

Положение 6. Тензор напряжений Коши упругого элемента вычисляется по формулам нелинейной теории упругости,

T =ρ ³ λ ^{i ∂} f n ⁱ ⊗ n ⁱ ,                                    (5)

i       k ik k k=1     ∂λik где ρ – плотность массы среды, n1i , ni2 , ni3 – ортонормированная тройка собственных векторов тензора растяжений i-го упругого элемента Vi ,

• V =   λ ⁱ n ⁱ ⊗ n ⁱ .

i      kk k k=1

В рассматриваемом примере (см. рисунок) массовая плотность свободной энергии f является функцией температуры θ , кратностей удлинений первого λ ¹₁ , λ ¹₂ , λ ¹₃ , третьего λ ³₁ , λ ³₂ , λ ³₃ и пятого λ ⁵₁ , λ ⁵₂ , λ ⁵₃ упругих элементов. Следует еще раз отметить, что мы не используем понятия деформационных градиентов для отдельных элементов схемы. Поэтому мы не можем говорить о том, что тензоры растяжения V ₁ , V ₃ , V ₅ появляются в результате полярного разложения соответствующих деформационных градиентов. Из последующих формул будет ясно, что тензоры растяжений V ₁ , V ₃ , V ₅ являются симметричными и индифферентными.

В дальнейшем для записи формул будем использовать точки над символами для обозначения производных по времени от величин при условии, что изменение рассматриваемых величин отслеживается для фиксированной частицы среды. Тот же смысл производной по времени для фиксированной частицы среды от выражения в круглых скобках будет иметь точка около закрывающейся скобки.

Массовая плотность свободной энергии f используется для вычисления тензоров напряжений Коши упругих элементов T ₁ , T ₃ и T ₅ . Для завершения описания поведения упругих элементов необходимо определить, как происходит во времени изменение тензоров растяжений. Для этой цели предлагается использовать следующее утверждение.

Положение 7. Для i -го упругого элемента производная по времени B _i от тензора деформации Коши – Грина этого элемента B _i = V _i ² вычисляется по формуле нелинейной теории упругости

B - B _z ( W R + W ^T) - ( W R + W ) B i = ^VD V            (6)

Общие вопросы неравновесной термодинамики с единственным уточнением. В классической теории упругости тензор Wi равен нулю. В предлагаемой нами формуле (6) дополнительный спин Wi является индифферентной антисимметричной функцией параметров состояния. Классический спин WR вычисляется обычным образом WR = RRT, где R - тензор поворота из полярного разложения деформационного градиента среды F = VR,

Положение 8. Дополнительный спин W _i упругого элемента, соединяющего левую и правую точки схемы, всегда равен нулю. Остальные дополнительные спины должны иметь нулевое значение при моделировании поведения среды в условиях совпадения ортонормированных троек собственных векторов тензоров скоростей деформирования упругих элементов и соответствующих им тензоров напряжений Коши.

Для материала, механическое поведение которого можно представить с помощью схемы, показанной на рисунке, дополнительный спин пятого упругого элемента равен нулю W 5 = 0. В результате уравнение (6) принимает для пятого элемента вид хорошо известной из теории гиперупругих сред. Дополнительные спины W ₁ и W ₃ служат для уточнения модели. Поясним это. Предположим, что мы смогли с высокой степенью точности описать поведение материала в большом числе экспериментов, в которых направление главных осей тензора деформации не менялось во времени. Встает вопрос. Будет ли модель работать в случае, когда направления главных осей тензора скоростей деформации меняются во времени и отличаются от направления главных осей тензора напряжений (например, в состоянии чистого сдвига вязкоупругой среды)? Если модель не будет удовлетворительно работать в этих условиях, то как ее можно уточнить? В нашем подходе есть возможность такого уточнения. Она осуществляется с помощью соответствующего выбора дополнительных спинов.

Следствие 1. Известные формулы теории упругости нелинейных сред для скоростей изменения во времени кратностей удлинения i -го упругого элемента

X‘k = Xkn\ ® n 1 ■ D                                          (7)

k kk k i и скорости совершения работы в этом элементе

T ■ D- = р £ # X к                           (8)

к=1 9Хк являются следствиями уравнения (6).

Символ скалярного умножения в равенстве (7) используется для обозначения операции скалярного умножения девятимерных векторов на множестве, которое образуют тензоры второго ранга. Докажем равенство (7). Используем для этой цели тождество

П к ® n к ■ ( n ‘j® n ij )* ^ 0, из которого следует равенство

--n k ® n к ■ B i = —n k ® n к Л1Л,”i ® n j ) ' = 2 ^ k .               (9)

^X к                   ^X к               j = 1

Поскольку B i = X ‘12 n i ® n 1 + X ‘ 22 n 2 ® n 2 + X ‘32 n 3 ® n 3 , скалярное умножение симметричного тензора на антисимметричный тензор равно нулю, справедливо тождество

Общие вопросы неравновесной термодинамики

¹ n ⁱ ⊗ n ⁱ ⋅ B ( W ^T + W ^T ) + ¹ n ⁱ ⊗ n ⁱ ⋅ ( W + W ) B =

λik    k i R i ik k R i i k                             λk

= ¹ _i ( n ⁱ k ⊗ n ⁱ k ) B i ⋅ ( W R + W i ) + ¹ _i B i ( n ⁱ k ⊗ n ⁱ k ) ⋅ ( W R ^T + W i ^T) ≡ 0.        (10)

λ _k                            λ _k

Умножим скалярно левую и правую части равенства (6) на выражение ( λ ⁱ _k )^- n ⁱ _k ⊗ n ⁱ _k .

Принимая во внимание равенства (9) и (10), получаем

λ ⁱ = ¹ ( n ⁱ ⊗ n ⁱ ) ⋅ VDV . i                i ii

λ _k

Преобразование правой части этого выражения

• ¹    ( n ⁱ ⊗ n ⁱ ) ⋅ VDV = ¹ B ( n ⁱ ⊗ n ⁱ ) ⋅ D =λ ⁱ n ⁱ ⊗ n ⁱ ⋅ D i k k i ii i i k k i kk k i

λk                      λk приводит к выводу о справедливости равенства (7), что и требовалось доказать.

Уравнение (8) вследствие 1 легко проверить, переписав правую его часть с помощью (7)

и используя формулу вычисления тензора напряжений Коши (5).

Механические свойства вязких элементов

Положение 9. Девиатор тензора напряжений Коши j-го вязкого элемента вычисляется по формулам теории нелинейной вязкой жидкости devTj=2ηjDj,                                                       (11)

где коэффициент сдвиговой вязкости имеет положительное значение η _j >  0 .

Механические свойства пластических элементов элемента

Положение 10. Девиатор тензора напряжений Коши пластического вычисляется по формулам теории пластического течения,

D n

D ⋅ D nn

^ dev T _n ⋅ dev T _n

dev T _n , n

где n – номер пластического элемента.

Для моделирования процесса необходимо исключить неопределенность в уравнении (12). Предлагается использовать для этой цели математическое выражение, которое связывает тензор скоростей деформирования пластического элемента с тензором скоростей деформирования среды.

Положение 11. Особенности механического поведения пластического элемента определяются пропорциональной зависимостью между интенсивностью тензора скоростей деформирования пластического элемента и интенсивностью тензора скоростей деформир ования самой среды,

Dn ⋅ Dn = κn VdevD ⋅ devD , где множитель κn ≥ 0 является неотрицательной функцией, заданной зависимостью

Общие вопросы неравновесной термодинамики

' 0,       при ^ф n ( V ,...) <  q n ,

^K n = 1

У q n ), при Ф n ( V ,...) = q n .

Функция текучести Ф _n , с помощью которой формулируется критерий развития в среде пластических деформаций, является функцией левого тензора растяжений V и других параметров состояния среды. Пластическое деформирование среды происходит в том и только в том случае, кода функция текучести имеет максимальное значение за всю предыдущую историю существования среды.

q n = max ^ф n ( V ,...).

Проверка выполнения неравенства диссипации

Определяющие уравнения модели должны приводить к автоматическому выполнению неравенства диссипации

T ■ D -p ( f + s 6 ) - h ■ grad ⁶ >  o,                                (13)

где h – тепловой поток, s – энтропия материала.

Положение 12. Энтропия материала s и тепловой поток h вычисляются по формулам неравновесной термодинамики s = -df, h = -c6 grad6,                                     (14)

d6

где c ₆ >  0 - коэффициент теплопроводности.

Докажем справедливость неравенства (13) для материала, иллюстрацией механического поведения которого является схема, показанная на рисунке. Для любого другого материала доказательство будет аналогичным. Раскроем значение скалярного умножения T ■ D , используя для этого формулу (3) и осуществляя ряд очевидных преобразований,

T ■ D = ( T i + T 3 + Т 5 ) ■ D = Т ■ ( D - D _s ) + Т ■ D в +

+ Т ₃ ■ ( D - D _c) + Т ₃ ■ D C + Т ₅ ■ ( D - D D ) + Т ₅ ■ D D .

В соответствие с равенствами (1) получаем

Т ■ D = У Т ■ D, + Т ■ D„ + Т ■ Dr + Т ■ Dn = ii 1B 3C 5D i=1,3,5

= Z Т= D i + Т 1 ■ ( D в - D C ) + ( Т 1 + Т 3 ) ■ D _c + Т 5 ■ D d .

i = 1,3,5

Принимая во внимание условия (2) и (4) и условие D D = 0 , приходим к удобной записи, имеющей простой физический смысл,

Т ■ D = ^ Т D i .                                            (15)

i = 1

Мощность работы действующих в среде напряжений равна сумме мощностей работы напряжений во всех элементах схемы механического поведения среды.

Формулы (5), (14) и (15) позволяют переписать неравенство диссипации (13). В результате оно принимает вид p X 6^к ^f-nк ® nк ■ Dz + Т2 ■ D2 + Т4 ■ D4 -p(f'+ S6) - h ■grad6 > 0 . k ik k i 2    2    4    4

i = 1,3,5 k = 1      O^ k                                                                   ⁶

Расписав производную по времени от массовой плотности энергии f

Общие вопросы неравновесной термодинамики

.

.

p f=p E E i=1,3,5 k=1

d f & i     d f &

Xk + p 6

dx k ^k d6

и используя равенства (7) и (14), получаем

T 2 • D 2 + T 4 • D 4 +

c 6 grad 6^ grad 6 >  0

Уравнения механического поведения вязкого (11) и пластического (12) элементов позволяют переписать рассматриваемое неравенство

_ dev T2 „      D4 • D4    . _

T ₂ ² + T ₄ • ----⁴—⁴---dev T ₄ +

2 q .           dev T ₄ • dev T ₄

Принимая во внимание тождество

c ₆ grad 6 • grad 6

> 0.    (16)

A • dev A = I -tr A + dev A | • dev A = dev A • dev A , v 3             J справедливое для любого тензора A, перепишем (16),

dev T2 • dev T2    1   D4 • D4     . „ . „ c6 grad 0^ grad 6 > 0

----²------² + ---- ⁴—⁴---dev T ₄ • dev T ₄ +

2 n 2          dev T ₄ • dev T ₄

Поскольку сдвиговая вязкость n ₂ и коэффициент теплопроводности c ₆ положительны, неравенство диссипации справедливо. Это и требовалось доказать.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований и Департамента образования и науки Пермской области (код проекта 04–01–96058), а также проекта фундаментальных научных исследований, выполняемых совместно учеными Уральского, Сибирского и Дальневосточного отделений Российской академии наук.