Дифференциальные уравнения кинетики некоторых химических реакций

Рассматриваются системы обыкновенных дифференциальных уравнений со специальной правой частью, в частности системы линейных и квазилинейных дифференциальных уравнений, а также асимптотическая устойчивость решений этих систем. Показано, что кинетика химических реакций, связанных с последовательными прямыми и параллельными реакциями, протекающими при постоянной температуре, описываются такими системами. Указаны условия, при которых вектор концентраций реагирующих веществ стремится к единственному стационарному состоянию при любых значениях начальных концентраций реагирующих веществ.

1.Постановка задачи

Обозначим через K" множество векторов x = (x1,x2,k,xn) действительного n -мерного векторного пространства R", координаты которых удовлетворяют условиям x > 0, (i = 1,2,k,n), £x = m.

i = 1

где число m >  0.

Рассмотрим систему обыкновенных дифференциальных уравнений

— = f ( t , x ),                              (1)

dt где правая часть f (t, x) = (f1 (t, x),..., fn (t, x)) удовлетворяет каким-либо условиям, обеспечивающим существование и единственность решений системы (1) в K". Требуется установить, при каких условиях система (1) описывает кинетику химических реакций, связанных с последовательными прямыми и параллельными реакциями, протекающими при постоянной температуре. Установить условия, при которых кинетика химических реакций стремится к единственному стационарному состоянию при любых значениях начальных концентраций реагирующих веществ.

• 2.Важные теоремы

Теорема 1. Если векторная функция f ( t , x ) удовлетворяет каким-либо условиям, обеспечивающим существование и единственность решений системы (1) в K ⁿ , то при выполнении условий

• а )    f ( t , x ) >  0 при x i = 0, ^ x k = m ,

k * i

• б )    f ( t , x ) ^ 0 при x = m , £ x k = 0,                    (2)

k * i

n

• в )    Ё ^{f (} t , ^x ) = ⁰ ,

i = 1

где m >  0 - число, то каждому начальному условию x ₀ е K" в момент t ₀ отвечает единственное решение системы (1) x ( t ) = x ( t , t ₀, x ₀), удовлетворяющее условию x ( t , t ₀, x ₀) е Kⁿ при V t >  1 ₀.

Доказательство . При условии 2в) система (1) имеет частный интеграл n

^ xi = m . Условия 2а) и 2б) показывают, что если начальные условия x ₀ i = 1

для системы (1) располагаются в множестве K", то и решение x(t) = x(t, 10, x0), системы (1) при t > 10, также будет располагаться в мно- n жестве K .

Замечание 1. Если векторная функция f (t, x) = A(t)x + b(t) линейна относительно компонент вектора x, то система (1) будет линейной системой dx

— = A (t) x + b (t), dt а условия (2) примут вид

• a )    a il ( t ) + b i ( t ) >  0, i * j ,

• б )    a ,, ( t ) + b i ( t ) <  0, i = 1, k , n ,

n

^в ) Ё [ a j ⁽ t ) ⁺ b '⁽ t ) ] = ⁰ , j = vK n .

i = 1

Теорема 2. Если матрица A и вектор b постоянны и все собственные числа матрицы A имеют отрицательные вещественные части и выполнены условия (4), то существует единственное стационарное решение p е K n системы (3). Все решения x ( t ) = x ( t , t ₀, x ₀) при x ₀ е Kⁿ системы (3) стремятся к нему при t ^ +^ .

Замечание 2. Рассмотрим систему квазилинейных дифференциальных уравнений dx

— = A ( t ) x + b ( t ) + ц f ( t , x , ц ). dt

Для правой части этой системы условия (2) примут следующий вид а ) a j ( t ) + b i ( t ) + ц f ( t , x , ц ) >  0, i * j , б ) a ii ( t ) + b i ( t ) + ц f ( t , x , ц ) <  0, i = 1, k , n , n

• ^в )    Е [ al l ⁽ t ) ^{+ b (} t ) ⁺ ц ^{f (} t , x , ц ) ] = ⁰ , ^j = ^K n , i = 1

при любом x е Kⁿ , t >  0 и любом це ( - ц ₀, ц ₀) , где ц ₀ >  0.

Пусть элементы a j . ( t ) матрицы A ( t ) и компоненты b i ( t ) вектора b ( t ) заданы при t >  0, вещественны и непрерывны, и пусть векторная функция f ( t , x , ц ) = ( f l , f ,, k , f ) задана при x e K n , t >  0, и це ( -да , +да ), вещественна, непрерывна и непрерывно дифференцируема по всем своим аргументам.

Теорема 3. Если выполнены условия теоремы 2 и условия (6), то существует положительное число ц ₀ такое, что при | ц | <  ц ₀ в системе (5) будет существовать единственное стационарное решение p е K" . Все остальные решения x ( t ) = x ( t , 1 ₀, x ₀) при x ₀ е K n системы (5) будут неограниченно приближаться к нему при t ^ +да . При этом скорость сходимости оценивается экспонентой.

Теперь рассмотрим приложения - кинетику химических реакций, связанных с последовательными прямыми и параллельными реакциями, протекающими при постоянной температуре.

Скорость реакции в газообразных смесях и жидких растворах при постоянном объеме представляет собой изменение концентрации данного вещества в единицу времени. Закон действия масс (основной закон химической кинетики) формулируется следующим образом [3]: если температура системы поддерживается постоянной, то скорость реакции в каждый момент времени пропорциональна произведению наличных, возведенных в некоторые степени, концентраций реагирующих веществ. А принцип независимости в химической кинетике заключается в следующем: если в системе протекает несколько реакций, то каждая из них подчиняется закону действия масс и протекает независимо от других реакций.

При изучении задач химической кинетики, связанных с последовательными прямыми и параллельными реакциями, протекающими при постоянной температуре, в силу закона действия масс и принципа независимости мы приходим к следующей системе обыкновенных дифференциальных уравнений nn

Э = Z Va i - ^ ,< = 1, K , n ,     (7)

dt j*i            m * i где x = (xpx2,k,xn) - вектор концентраций реагирующих веществ Ai (i = 1, к, n) в момент времени t > 0, kj > 0 - концентрации скоростей реакций Aj ^ Ai, i * j, aj (целые положительные числа) - порядок реакции Aj ^ Ai,i * j. Правая часть системы (7) удовлетворяет условиям (2).

Если aj = 1, i, j = 1,к, n, то все реакции Aj ^ Ai , i * j, являются реакциями 1-го порядка и система (7) будет линейной dx

— = Kx ,                          (8)

dt где K = {kj} - квадратная матрица, имеющая вид

' kj, i * j, kj =<

n

• ^k.. =^- E ^kj .

.           j *

Таким образом, кинетика последовательных и параллельных реакций 1-го порядка реагирующих веществ A i ( i = 1, к , n ) описывается линейной системой (8) дифференциальных уравнений с постоянными коэффициентами, правая часть которой удовлетворяет условиям (4).

Если все реакции являются реакциями одного порядка, то есть a1} = a > 1, i, j = 1,к,n, то система (7) запишется в виде n

• -i-    = Z j J , i = 1, - , n .              (9)

—t     = 1

С реакциями с порядком выше третьего практически не приходится встречаться [3]. Рассмотрим некоторые частные случаи системы (9).

Пусть A1 ——^ A2 - прямая реакция 2-го порядка, где к - константа скорости реакции A1 ^ A2, A1 - исходное вещество, A2 - продукт. Обозначим через x1(t), x2(t) концентрации веществ A1,A2 соответственно, тогда уравнение кинетики прямой реакции 2-го порядка имеет вид

< x i =- kx,, x ₂ = kx 2 .

Последовательные реакции 1-го порядка: A 1 —— ^ A ₂ сываются следующей системой

' ^xi = ^{- к} i ⁵ 1 ,

* 5с 2 = к 1 x 1 - к 2 x 2, x 3 = к 2 x 2.

k

---> A 3 опи-

Уравнение кинетики параллельных реакций 1-го порядка на рис.1

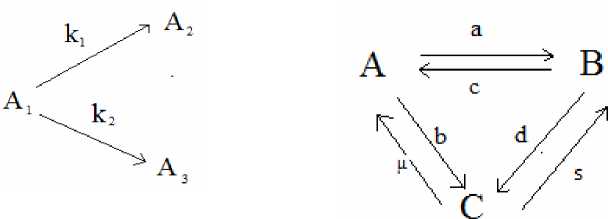
Рис.1.                                 Рис.2.

имеет вид

' x i =^{- ( к} i + ^к 2 ) x i ,

< x 2 = к 1 x i ,                                           (12)

,x ₃ = к ₂ x 1 .

Обратимые реакции

A1   к' > A 2 и A 2 ——^ A1, где реакция A1 ——^ A2 имеет 2-й порядок и обратная реакция A2 ———> A1 также имеет 2-й порядок, описываются следующей системой нелинейных дифференциальных уравнений

1      2 . 1     .2

x 1 = - к 1 X j + k ₂ x ₂,

x₂ = к 1 X 1 ² - к ₂ x 2 .

Предположим, что ку > 0, i, j = 1,k,n, i * j,

и исследуем решения системы (9) на асимптотическую устойчивость в n множестве K .

Теорема 4. Если все константы скоростей k ij >  0 реакций

Ai ^ Ay, i * j, отличны от нуля, то в системе (9) существует единствен ное стационарное решение p е K" и все остальные решения

x ( t ) = x ( t , t ₀, x ₀) при x ₀ е Kⁿ системы (9) стремятся к нему при t ^ +^ .

Доказательство. Из условий (14) следует, что для любого 10 > 0, любого i = 1,..., n и для любого решения x(t) = x(t, 10, x0), где x0 = x(10) е Kn, выполняются соотношения:

xi (t) > xi (10) (i = 1, ..., n) при t > t0.

t >  1 ₀ и всех i = 1, к , n .

Взяв 3 = min x, ( t ₀), получим, что x ( t ) >  3 при I " l <  n

Систему (9) перепишем в следующем виде dx dt = C(x) x , где матрица C(x) = {cij (x)} имеет вид cij(x) = ’

k j x a j

n

, i * j ,

-У к -xami mii

,

i = j,

и обладает свойствами: внедиагональные элементы матрицы C(x) неот- рицательны и сумма элементов по каждому столбцу равна единице.

Таким образом, система (9) будет асимптотически устойчивой в K ” . Но множество K ” является выпуклым ограниченным и о - инвариантным [2]. Тогда из теоремы Брауэра о неподвижных точках [2] следует, что в множестве K ” существует стационарная точка системы (15). Отсюда следует, что при выполнении условий теоремы существует единственное стационарное решение в системе (15) и все остальные решения стремятся к нему при t ^ +да . Теорема доказана.

Применив теорему 4 к системе (13), получим, что и в этой системе имеется единственное стационарное решение

Р 1 =

m

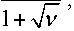
Р 2 =

m V

1+V ’

k где v = -1, к2

и все остальные решения в системе (13) стремятся к нему при t ^+да , если начальные условия удовлетворяют условиям x о >  0, У о >  0, x о + У о = m .

Рассмотрим химическую реакцию на рис. 2. Здесь a,b,c,d,s являются константами скоростей реакций 1-го порядка, а ц является константой скорости реакции 2-го порядка. Кинетика такой реакции описывается системой квазилинейных дифференциальных уравнений dxi     7 П         .2

—1 = -(a + b) x j + cx2 + цx3, dt              ' 1     2

dx^.

• <—- = ax ,-(c + d) x2 + px3,(16)

dt     -    ' 23

dx

• -j³ = bx 1 + dx ₂ - sx ₃ - ц x ₃, правая часть которой удовлетворяет условиям (6).

По теореме 3 следует, что существует положительное число ц ₀ такое, что при 0 <  ц <  ц ₀ в квазилинейной системе (16) будет существовать единственное стационарное решение p е K ³ , и все остальные решения x ( t ) = x ( t , t ₀, x ₀) при x ₀ е K ³ этой системы будут приближаться к нему при t ^ +да . То есть, если концентрация скорости обратимой реакции 2го порядка C ^ A достаточно мала, то при любом значении начальных концентраций реагирующих веществ химическая система стремится к единственному стационарному состоянию.

Заключение

В статье показано, что кинетика химических реакций, связанных с последовательными прямыми и параллельными реакциями, протекающими при постоянной температуре, описываются системами обыкновенных дифференциальных уравнений, правая часть которых удовлетворяет условиям (2). Изучены свойства решений таких систем.