Дифференциальные уравнения начала движения упруго связанных инертных тел на примере поезда с упругими сцепками

Сила трения покоя значительно превосходит силу трения движения. Это приводит к тому, что режим трогания для наземного транспортного средства является наиболее тяжелым. Для поездов этот режим представляет настолько серьезную проблему, что иногда приходится принимать специальные меры, такие как использование песка в зоне контакта бандажа колеса с рельсом или вспомогательного локомотива [1].

Эффективным способом трогания поезда является выбор зазоров в сцепках. При этом вагоны приводятся в движение последовательно и инертная масса, а также сила трения покоя непосредственно в момент трогания минимальны.

Этот способ, однако, имеет два существенных недостатка – малую фиксированную величину зазоров в сцепках, что ограничивает эффективность способа и ударный характер передачи импульса, а это, в свою очередь, секция; локомотив; вагон; колебания; демп- отрицательно сказывается на состоянии конструктивных элементов поезда.

Указанных недостатков можно избежать, если использовать упруго деформируемые сцепки [2, 3].

Целью работы является построение математической модели "легкого" трогания поезда с упругими сцепками.

Расчет механической системы в составе массивных локомотива, вагонов и упругих сцепок является достаточно громоздким. Для его минимизации принимаются следующие допущения: сила F , развиваемая локомотивом, – величина постоянная; массы локомотива и вагонов равны между собой и составляют m .

Локомотив и один вагон

Уравнение сил, приложенных к локомотиву, имеет вид: ²

F = mdx ⁺ k ⁽ * — * 2 ^},       (1)

где x , x – перемещение, соответственно, локомотива и вагона, k – коэффициент упругости сцепки.

Силы, приложенные к вагону, удовлетворяют уравнению

Поэтому для t = 0 последнее выражение примет вид z (0) = 0 = C cos

J2—0 + C sin. 2—0 + — m        m  2m d2x

0 = m ^ ₂² - k ( X j - x ₂).

Из последнего уравнения следует:

откуда             C 1 =-- .

2 m

С учетом этого

m d ² x

* 1 =-- 22

¹ k  dt ²

z =

F --cos 2 m

k    kF

A2 —t + C2 sin /2 —t + — m        m 2m

Подстановка этого выражения в (1) дает

m ² d ⁴ x     d ² x     d ² x

F =-- F + m —-2 + m —-2 + kx₂

k dt ² dt ² dt ²

—

kx₂ =

Пусть

_m 2 _d 4 _x

k

dt ²

A + 2 m dt2

.

_d 2 _x

---2 = z .

dt ²

Тогда (3) запишется в виде z" + 2-z = kF .

mm ²

Характеристическое уравнение r2 + 2 — = 0.

m

В соответствии с (4)

Fmk v2 = I zdt =--./—sin. 2 —t —

2         2m 2km mkF

C2 9 7 cos A2 t + t + C3 , 2km

Fk x2 = I v2dt = —cos. 2—t —

2 J 2

—Cm sin.2 —t + — t2 + C3t + C.(7)

2k     m4

С учетом (2), (4), (6) и (7)

Его корни равны

r i,2 =± i\ 2-

Общее решение соответствующего однородного уравнения

Z j = C j cos

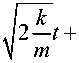
t .

X =— — cos J2-1 + C2m sin J2-1 + — + 12k      m    2k      m2

Fkmk

+-- cos. 2 — t — C, —sin. 2 — t +

4k      m    2 2km

F

+--1 + Cd + C., 4m dx   F   kk v = —- = — . 2 — sin. 2 —t + dt  2k   mm kmk

+C2 22--cos./2 —t — mkm

Частное решение в соответствии с (5)

—

■ t + +

имеет вид           z₂ = A .

Подстановка его в (5) дает

F

2 m

2 ^— A = ^kF , mm

Откуда          A = — .

2 m

Общее решение уравнения (5) находится как

Z = Z j + z₂

k    kF

= C cos /2 —t + C2 sin J 2—t + mm

В момент времени t = 0 сцепка не деформирована, следовательно, на вагон сила не действует и величина (4) равна нулю.

dv   F  k      k      k mk fj = —- = —2 — cos /2 —t — C2 2--sin /2 —t — dt  2k m     m     m km

F k     k     km    kF

--2 — cos./2 —t + C2 2--sin J 2 —t +

4k m     m     m 2k     m2

x2 (0) = 0 = —cos 2 — 0 — m . I F .

• — C ₂— sin. 2-0 + — 0 ² + C 0 + C ,

• 2 2k       m    4m      34

FF

— + C = 0, C =-- v2(0) = 0 = -с2 m + С3,

2 k

F п

+---

2 m 2

v 1 (0) = 0 = С 2

km m2k

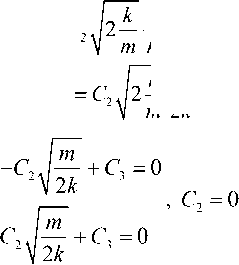
С = 0.

^т + с =

2 k    ³

Окончательное решение:

Уместно сравнить эти показатели с соответствующими величинами для недеформируемого состава.

F a = —, 2 m

^X (^Т 2 ) =

F      F 2

v = 2 т¹ ’ x = 4 т¹ ’

F п² т _ F п² ■ 4 т т—” з— ’

x i =

F

2 k F

—

— cos. — t + — t

4 k

m  4 m

F

⁺ 4k ’

/  . F п т v (Т2 ) = 2т-\2k = -

X 1 ( Т 2 ) _ F п ²/(32 к ) + F /(4 к )

x (^Т 2 )

F п ²/(32 к )

F п

= 1 + -Зу - 1,81,

4 -

F x, = — cos

2   _{4 k}

2 k F

A— t +—t m  4m

—

F

4 k ’

v 1 ( т ₂) _ f/ (242km ) + F П (442кт ) _

v ^(Т 2 )

v

F      2 k

1 = —i=^sini — t 22 km   m

F

■ t +-- 1 ,

2 m

F п/ (442 кт )

= 1 + - » 1,64 . п

F      2k F v2 =--.-----sin. —t +--1 ,

22 km   m 2 m

F a. = — cos

¹   2 m

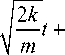
Отношение для кинетических энергий локомотива [4] составляет

E

J' = 2^,69.

E (^Т 2 )

a₂ =

F

--cos

2 m

2 k   F

----1 +-- m  2m

Характерный отрезок времени  т2

(индекс " 2 " означает количество составных частей поезда) для рассматриваемого случая

Полученные соотношения демонстрируют, что трогание упругими сцепками значительно недеформируемого.

Локомотив и два вагона

наглядно состава с легче, чем

определяется из условия максимального растяжения упругой сцепки. При этом

Уравнения сил, приложенных, соответственно, к локомотиву и вагонам, имеют вид:

F а (ъ)--= 0 или

2 m

F 2 k

---cos —т₂ = 0 , 2 mm

d ² x

F = т —^ + к ( X j — x ₂),

V 2 - ’ 2 = ^П , m 2

За время т2 расстояние

^Т 2 =

локомотив пройдет

d2x к (Xj — x2) = т   2 2 + к (х2

d2x к (х 2 — х3) = т -2-

—

.

^X 3 ) ,

x ₁

( ^Т 2 ) =

F   2k: п тй

— cos.-- А --+ 4 k     m 2  2 k

Из последнего уравнения следует:

m d2x х2 =--Г3 + X, .

² k dt ^{2     3}

F п ² m  F  F п ²   F

+-----1--=--1--

4 m 4 2 k  4 k  32 k  4 k

Производная этого выражения равна

и разовьет скорость z .    f .  /2— п та v (т ) = —j^sin,--А--+

¹²   22 km   m 22 k

d ² x    m d ⁴ x    d ² x

"dt ²"= ~к~йй~ й^

.

Подстановка последних двух выражений в (9) дает

m d ² x

• x =--г² + 2 x, - x =

• 1    k dt2       23

m2 d4x   m d2xm d

13 ++ 2+ 2 x3 - x3 = k2 dt4   k dt2    k dt233

m2 d4xmd

=     г + 3г + x.(11)

k2 dt4      k dt23

В соответствии с (13)

v = j zdt = C

+ C

Производная этого выражения равна

d ² x   m ² d ⁶ x    md ⁴ x   d ² x

—г- = —;3 + 3-- 3- + —-³.

dt ²     k ² dt ⁶       k dt ⁴      dt ²

Подстановка полученных выражений в (8) дает

■ t +

■ t + 1 + C ,

3 m      ^{5 ,}

m     3k     m3

x3 = I v3dt = -C —cos. —t - C2 —sin —t -3k     m     3km mkmk

- C —cos./ —t - C —sin. —t + kmkm

F  m3 d6x    m2 d4xm d

• — = ^--r + 3—;--X ++

k   k ³ dt ⁶      k ² dt ⁴

m2 d4x    m d2xm d

+-;+ 3+ x3- x k2 dt4      k  dt2     3k dt2

m3 d6x    m2 d4xm d

=--3 + 4--3 + 3

k3  dt6      k2  dt4      k dt2

d ⁶ x     k d ⁴ x     k ² d ² xk

--Г + 4--4 + 3—т—Г = —; . (12) dt6     m dt4     m2 dt2

Пусть       dx- = z.(13)

Тогда (12) запишется в виде z"' + 4-z" + 3—z = kF .(14)

mm

F 2

+—t2 + Ct + C . 6m

С учетом (10), (13), (15) и (17)

m      3k  m3

x2 = —C cos. —t + — C sin —t + k   mkm m     k  m     kmF

+ — C cos. —t + — Csin. —t +-- k      m  k      mk

—

m     3k     m3

^- C i 77^cos\ — t ^- C 2 77^sinA — t ^-

3k     m     3km mk

- C3 — cos. —t -km m    k F2

-C4  sin. / 1 +--1 + Ct + C = k    m 6m

Характеристическое уравнение kk r4 + 4—r + 3—- = 0.

mm ²

2    kk    2    k2

ri 2 = -2 — ± — =, X = -3— , r, =,

,   mm      mm ri,2 =±\I3 k , r3,4 =±i\~ .

mm

Общее решение соответствующего

2 m       3 k   2 m       3 k

= 4FC1 ^cos \ ^_ t ⁺ ЧТ ^C 2 ^sin \ ^_ t ⁺ 3 k       m   3 k       m

F F ,

+ — +-- 1 ² + Ct + C ,

56 ^,

dx v 2 = —2 dt

2 m  3 k       3 k

\—C i ^sin\ — t ⁺

3 k  m      m

однородного уравнения

2 m

+--

3 k

F

■ t +— t + C =

3 m     ⁵

+C cos z1 = C cos

—

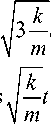
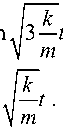
■ t +

+

F

■ t +-- 1 + C ,

3 m      ^{5 ,}

Частное решение имеет вид z ₂ = A .

Подстановка его в (14) дает k2    k2F      F

³ A        , A      .

m ² m ³ 3 m

Общее решение находится как

3k3k z = z{ + z2 = C cos. —t + C2 sin. —t + mm

dv             3k a2 = —2 = -2C cos J—t - 2C2 sin dt            m

3 k

F

-----1 +--.

m

С учетом (11), (20), (18) и (17)

m    3 k      m    3 k

X j = - 2 C —cos. — t - 2 C ₂ —sin. — t + km km

3 m

Fm

---+

3 m k

k    kF

+ C ₃ cos. — t + C ₄ sin —t + — .

m       m 3 m

2 m      3 k    2 m      3 k  2 F

+ 2 — C , cos. — t + 2— C sin. —t +--

3 k  ¹ m     3 k  ² m    3 k

2F , + — t 2 ++ 2 C 6 m	m     3 k t + 2 C 6 + C 1 TT cos J   t + 3 k     m
m + C, —sin. 23 k	3 k     m /—t + C 3 —cos. m    3 k	/kt + m
m + C 4 k   v	k   F 2 —t--1 — C-t m  6 m	— C 6 —
m     3 k     m    3 k — — C 1 cos А _ t — C 2 77 sin А _ t 3 k     m     3 k    m
m + C 3 — cos,	km J-t + C 4 — sinJ mk	k —t + m

F      3k v — —;=sin< —t + 6 3km    m

t + —t , 3 m

v2 = v3

—

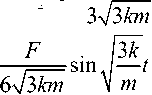
3kF nJ—t+ —t, m3m

FkF

--/= sin./ —t +

2 km    m3

F    3k F ax — — cos J—t +--cos 6m    m  2m

k

F

t +     , m 3m

F    3k   F a2 —--cos J—t +— , 3m    m  3m

v 1 =

dx dt

F F „

+- + — t ² + Ct + C ,

56 ^,

= C 1

t

—

m  k   m  kF

^{— C} 3 J T sin J- t ^{+ C}4'T cos J— t ⁺ —t ^{+ C} 5 .

k    m      k    m 3 m

F

3 k

a ₃ — — cos J— t —

6 m    m

F cos 2m

k

F

—t +--.

m 3 m

Характерный отрезок времени т3 для

a_x — C cos

3 k

—t — C ₃ cos m

k

F

—t +-- m 3m

В соответствии с (20)

FF a2 (0) — —2 C + — = 0, C = —. 3m6

В соответствии с (15)

F FF z (0) = 0 = — + С + —, C =.

6m3  3m3

рассматриваемого случая определяется из условия максимального растяжения упругой сцепки.

При этом

F ai (Т )

3 m

F     3k    Fk или --cos Л --Т +--cosj—Т — 0 ,

6m    m   2mm

1 kk

- cosV3.—т₃ + cos. —т₃ — 0.

3 mm

Решение последнего уравнения имеет вид:

В соответствии с (18)

x (0) = -mC. + — + C = 0,

²        3 k ¹    3 k ⁶

J - т₃ = 0,427 п , m

т₃ = 0,427 п

За время т3 локомотив пройдет расстояние

F F           4F

—+— + c₆ = 0, C = — 9 k 3 k ^{6       6} 9 k

В соответствии с (21), (16) и (19)

v - (0) = ^r-C 2 + C 5 = ⁰, C - = ⁰, C 5 = ⁰.

3 k

Окончательное решение:

F     3k        m x (т3) —--cos.--0,427л. —

¹³     18 k     m ^,       k

—

—

F cos

2 k

m^⁷¹* f⁺

F

+— 0,427 п 6 m

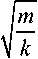
5 F

+--—

9 k

^— — —cosj3 - 0,427 п — k 18

F     3 k	F  kF	5 F
x, —-- cos. —t — 1     18 k      m	— cos —t + — t 2 k    m  6 m	+-- 9 k
F x2 — — cos. 2   9 k	3 k   F 2   F ----1 +-- 1 --, m   6 m   9 k
F     3 k x3 —-- cos. —t + 3     18 k     m	F  kF — cos —t + — t 2 k    m  6 m	4 F 9 k

— cos 0,427 п + - ( 0,427 п ) ² + -

₂       ,          ₆ ,             ₉

^— — —cosj3 - 0,427 п — ^-cos0,427 n +

- 18           ’         2      ,

1                     S

+ 6 ( ^0,427 п ) + 9

F — 0,78 — к

и разовьет скорость

F      3km

^{1(Т з )} " 6Ж ^!'N m ’ ^0,427л k

+—sin. ^ • 0,427n m +—0,427n 2 km    m        k3

F (1

.— I —7=sinV3 • 0,427n + 4km v 6V3

1 .               1

+ -sin0,427 n + -0,427 n 1 =

2          3

.

Уместно сравнить эти показатели с соответствующими величинами для недефор-мируемого состава:

F

3 m

F      F 2

v = 3 m ’ x = 6 m⁽ ’

x ( T ) = ^{— (} 0,427 n m

6 m V       V k J

= ⁰’³ F

F      m F

v(t ) = — • 0,427л. m = 0,45 -== 3mkmk x-W =26 x (’3)     ’ v1 (T3 ) v(T3 )

= 2,22.

Отношение для кинетических энергий локомотива составляет

E 1 (^T 3 ) E (^T 3 )

= 4,93.

Заключение

Применение упруго деформируемых сцепок решает проблему трогания тяжелого поезда.

В таблицу сведены перемещения, скорости и кинетические энергии локомотива для моментов максимального растяжения упругой сцепки, отнесенные к соответствующим параметрам недеформируемого состава.

Приведенные перемещения, скорости и кинетические энергии локомотив а

Количество секций поезда	x 1 (T) x (t)	v 1 (t) v (t)	E 1 (t) E (t)
2	1,81	1,64	2,69
3	2,6	2,22	4,93

Полученные соотношения наглядно демонстрируют, что трогание состава с упругими сцепками значительно легче, чем недеформируемого. При этом, чем больше число вагонов, тем больше преимущество первого над вторым.

Смягчение режима трогания состава по существу обусловливается заменой одновременного трогания секций на поочередное. Выше этот процесс описан для инерционных сил. Применительно к силе трения покоя механизм будет подобным, т.е. преодолевается не вся сила трения покоя одновременно, а поочередно преодолеваются ее малые части.

Полученные выражения для перемещений, скоростей и ускорений локомотива и вагонов имеют гармонические составляющие [5–7]. Для исключения продольных колебаний [8–10] состава после достижения максимального растяжения сцепки следует механически блокировать возможность ее гармонического сжатия с последующей выборкой упругой деформации, например, с использованием демпфирующих устройств.