Differential evolution algorithm for optimizing virtual machine placement problem in cloud computing

Published Online July 2018 in MECS

Cloud computing is a technology that provides on-demand services over the internet such as computing resources, data or software. The cloud computing has four deployment models i.e. public, private, hybrid and community. Software as a Service (SaaS), Platform as a Service (PaaS) and Infrastructure as a Service (IaaS) are the three important service models in cloud computing. Cloud providers have large computing resources in large data centers which are available to users on a per-use basis [1]. A data center is a group of physical machines or hosts. Each physical machine has computing capacity, memory, bandwidth, and storage capacity [2].

Today, cloud computing is one of the most explosively expanding technologies in the computing industry. Therefore, the number and the scale of cloud service providers greatly increased. More data centers mean more energy supply and higher operating costs. It places a heavy burden on both environment and energy resources. Optimization is essential for cloud computing providers to provide a good value to potential customers. The placement of virtual machine in cloud infrastructure is one of the main research problems. The execution or placement of virtual machine on each physical machine of the data center is the process which is called virtual machine placement. In other words, placement of virtual machine is to choice the most appropriate host designed for the virtual machine process. The placement of virtual machine has many objectives like a minimum number of physical machines used, effective usage of power consumption and resource utilization such as CPU, memory, and bandwidth. The problem is how to accomplish utmost of these properties in a allocating of the virtual machine structure, to have extra efficient, little overhead, short cost and scalable allocates of virtual machine in the cloud data centers. However, approximately of these objectives are in conflicting with each other and wholly of them may not completely be attained in one allocating scheme [2-4].

In this paper virtual machine and physical machine is measured in three-dimensional item such as CPU size, memory size and storage size. The allocation of the virtual machines taking place physical machine is similar to the 3D bin packing problem. In three-dimensional bin packing problem, a group of 3D items is necessary to be placed inner side 3D bins. The main goal of this problem is to pack as more as possible items in the bins, so that the minimum count of bins are essential. In bin packing problem two items can be placed into bins beside each other or one on top of the other but this is impossible operation in a placement of VMs. The placement of virtual machine problem is similar to Vector Packing Problem and it is also an NP-Hard problem [5, 6].

The placement of virtual machine problem is constrained optimization problem, where the objective is to allocate virtual machine to physical machine by satisfying given constraints. The problem is ‘P’ problem means when the problem size is small i.e. quantity of physical machines (PMs) and virtual machines (VMs) are less. Problem complexity increases with the size of a problem. When the number of virtual machines and physical machines are big enough, the situation becomes difficult to manage. Even in the automatic calculation of the placement plan, the combinations are large for a given number of virtual machines and physical machines. Such an enormous solution space creates it an NP problem. Literature reports that it is nearly unbearable for brute force algorithms to complete the physical and virtual machine mapping optimally within acceptable time. Therefore, the needs for intelligent placement of heuristics to narrow the search for solutions to get close to the best placement plan [7]. Heuristic algorithms such as Genetic Algorithms, Particle swarm optimization, Ant colony optimization are good candidates which has the ability to find sub-optimal solutions in finite time.

In cloud computing work, virtual machine placement problem is studied from different perspectives. The problem is studied with different objectives, constraints and addressed by different traditional and heuristic algorithms [2, 3]. In this paper, the problem is expressed a single-objective optimization problem with resource constraints. Objective of this paper is to apply Differential Evolution algorithm and identify suitable operators for VMP. The results are compared with random fit algorithm and best- fit algorithm.

The paper is arranged as follows: Section II presents the background of virtual machine placement problem and different problems solved using Differential Evolution algorithm. Section III describes the virtual machine placement problem. Section IV describes the best fit, random fit and Differential Evolution algorithm. Section V presents dataset generator for problem instances and results obtained by best fit, random fit and Differential Evolution algorithm. Finally, the conclusions of our study are outlined in Section VI.

• II.    Related Work

In cloud computing work, the virtual machine placement has been broadly studied. Some of the important issues addressed in literature are energy efficiency, specific architectures and performance of placement algorithms comparing with different methods [8]. The problem is formulated with heterogeneous as well as homogeneous virtual machine and physical machine [3, 9].

Different researchers considered different objective function for placement of virtual machine problem in cloud computing such as, minimize energy or power consumption, minimize number of physical machines [46, 9, 10-12], minimize network traffic [6, 5, 10, 13, 14], minimize economical cost or operational cost [5, 15-17], maximize performance and resource utilization, reduce wastage resource [4, 7, 18], improve utilization of cloud resources, maximizing providers’ revenue, decreasing cost for cloud providers and growing the return on investment (ROI), improving load balancing, high performance, throughput and response time [7].

Many researchers found that why energy efficiency is important in cloud data infrastructure [9]. They have firstly identified sources of energy wastage in data centers then to overcome energy wastage they made a plan of work. This plan of work analyses how to manage energy efficiency in data center and design problem formulation for this issue.

In literature, there are many techniques used to solve placement problem of virtual machines such as constraint programming, stochastic integer programming, greedy algorithm, heuristics based algorithms, game theory based algorithms and graph theory based algorithms.

The constraint programming is beneficial for combinatorial search problems and its solutions strictly fulfill the constraints on dealings among variables. Stochastic integer programming is applicable for forming optimization problems. Author proposed optimal virtual machine placement to deliver resources of several cloud providers and minimize cost for placing the virtual machine on a physical machine [3, 9].

Greedy algorithm is one of the traditional algorithms used for solving the placement problem of the virtual machines. These algorithms necessity fewer polynomial time complexity than the meta-heuristics algorithm and it can be executed straightforwardly. In virtual machine placement problem first-fit decreasing is one of the famous greedy algorithms, placement of virtual machine is sequential. Another traditional algorithm is the best fit, random fit and next fit. In random fit algorithm randomly select a physical machine to place virtual machine on it.

Heuristics algorithms are considered as new good candidates who are able to find near optimum solution for the problem [19]. In [20], authors proposed genetic algorithm for single objective virtual machine placement problem. The objective is cost minimization for physical machines. Results show that genetic algorithm is better than the first-fit decreasing algorithm. In many papers it is found that heuristic based techniques are better [4, 5, 7, 12, 21-25].

Paper [26], tested performance of three evolutionary algorithms namely Differential Evolution (DE), Genetic Algorithms (GA) and Particle Swarm Optimization (PSO). Results show that as compared to GA and PSO, the DE has the least clustering and re-initialization effect. Also DE did not have any influence (that is a dominant influence) on population. Different problems are solved using Differential Evolution algorithm such as scheduling and resource allocation [27-32], clustering [33, 34], scheduling of the hydro power generator [31]. Santucci V. et al. [28], proposed Differential Evolution for variation flow-shop scheduling problem with the overall flow time criterion. For the mutation operator, they used the biased selection strategy, mimetic restart procedure, and heuristic based initialization. To do the analysis they have done the performance comparisons with the widely accepted benchmark suite. Zhao M. et al. [35], has done the research on the constrained optimization problem using multi-objective Differential Evolution algorithm.

• III.    Virtual Machine Placement Problem

In cloud computing, virtual machine placement is one of the most demanding problems. It has a direct effect on the performance, resource utilization and power consumption of the data centers and can reduce the maintenance cost of the data centers for cloud providers. Numerous VM placement schemes are designed and proposed for VM placement in the cloud computing environment aimed to improve various factors affecting the data centers, the VMs and their executions.

The objective of this paper is to minimize the required number of physical machines to place all the virtual machines by satisfying resource constraints. In literature, many researchers worked to achieve similar objective [46, 9, 12-14]. The minimization of required physical machines leads to maximize CPU, memory, bandwidth utilization, electricity and cost minimization.

In this problem formulation, we have considered physical and a virtual machine with three attributes namely CPU i.e. computing capacity, memory and bandwidth. The set of a physical machines and virtual machines with their resource capacity are known.

The objective of placement virtual machine problem is to minimize set of physical machines required to place all virtual machines by following constraints,

• 1.    Capacity Constraints:

• 2.    Placement Guarantee Constraints:

For each dimension of a physical machine, the summation of the resource requirements of all virtual machines allocated should be fewer than or equivalent to the total accessible capacity of that physical machine. VM i place on PM m indicates 1 otherwise 0.

All the virtual machines must be located on the physical machine.

Capacity constraint and placement guarantee constraints are hard constraints which must be fulfilled. Violation of these constraints (also called as conflicts) will reason the solution to be infeasible.

• IV.    Alogrithms

This section presents algorithms experimented to solve virtual machine placement problem. This paper presents comparison of best fit algorithm, random fit algorithm and Differential Evolution algorithm.

• A.    Random Fit Algorithm

In the random fit algorithm, allocates random physical machine which is big enough for allocating virtual machine with satisfying all constraints [36]. Fig. 1 shows random fit algorithm for solving virtual machine placement problem.

• B.    Best Fit Algorithm

In best-fit algorithm, allocates the available smallest physical machine which is big enough for allocating virtual machine with satisfying all constraints. The smallest physical machine is which results in minimum resource wastage [36].

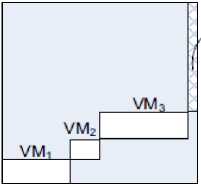
The meaning of resource wastage and its calculation technique are taken from [37]. The remaining resources accessible on each host may differ greatly depending on the virtual machine placement solution. Unbalanced remaining resources may stop any further VM placement, therefore wasting computing resources. The cross-shaded area in the figure represents the remaining resources that can be used for upcoming allocation.

Random Fit Algorithm

Input: A Number of VMs and Resource requirement of each VM.

Number of PMs and capacity of each PM.

Output: Number of PMs required allocating all VMs.

for all VM i=1 2 n do while VMi assigns to any PM

PMj ^ Select PM randomly if PMj satisfies all the constraints then assign VMi to PMj.

calculate the remaining capacity of PMj end if end while end for

• Fig.1. Random fit algorithm

  CPU

  
  
  

  Residual capacity

  Total capacity

  Fig.2. Resource wastage [37]

  
  

  Memory

  
  

In the example of Fig. 2, the host has many idle CPU capacities, but the available memory is very small, causing the host to accept any new VMs due to insufficient memory. To balance the usage of resources in different dimensions, use the following symbols to calculate the potential cost of wasting resources. R_i denotes the normalized remaining resource with dimension i . The subscript k is used to recognize the dimension with the least normalized remaining capacity and the remaining resources wasted on the server are calculated as the sum of the minimum normalized remaining resources and the difference between the other resources [37].

The relationship among W and resource remaining is linear. Extra remaining resource variances in dissimilar dimensions, the more resources are unused.

W = Z ( R i - R k )                (1)

i * k

Fig. 3 presents best fit algorithm for solving virtual machine placement problem.

Best Fit Algorithm

Input: A Number of VMs and Resource requirement of each VM.

Number of PMs and capacity of each PM.

Output: Number of PMs required to allocate all VMs.

for all VM i=1,2,……n do while VMi assigns to any PM

PMj ^ Select best fitted PM based on minimum resource wastage if PMj satisfies all the constraints then assign VMi to PMj.

calculate the remaining capacity of PMj end if end while end for

• Fig.3.    Best fit algorithm

• C. Differential Evolution Algorithm

Differential Evolution algorithm is an evolutionary algorithm. The DE algorithm is used for global optimization. The main advantage of DE algorithm is improvement takes place in the solution after individually iteration. Differential Evolution's theoretical framework is simple and it has or requires the fewer algorithm parameters but that performs well in convergence. In the Differential Evolution solution space is denoted in D-Dimensional vectors and this space is denoted as a real number. Differential Evolution algorithm fulfills four requirements of user for minimization techniques such as ability to handle nonlinear, non-differentiable, multimodal cost functions, parallelizability to cope with computation intensive cost functions, ease of usage and good convergence properties [38]. Fig. 4 presents DE algorithm.

As compared to the Differential Evolution (DE) algorithm, genetic algorithm (GA), particle swarm optimization (PSO) has two main advantages such as improvement takes place in the solution immediately after each iteration and requires fewer number of algorithm specific parameters [26].

In the DE Initial vector is the size of n in Ddimensional. The new solution is generated by merging the several candidate solutions. New population generation is done in repeated cycle by using the three DE operators such as mutation, crossover, and selection. Generating the trial vector is a key process in DE, the generation of the trial vector by using the candidate vectors is done by using 2 steps:

Differential Evolution Algorithm

Input: A Number of VMs and Resource requirement of each VM. Number of PMs and capacity of each PM, I max = number of iteration.

Output: Number of PMs required to allocate all VMs.

Initialize: a sequence of VM randomly V o , I max .

Calculate the initial fitness function value (V o , P);

While t

trial vector = mutation (3 random candidate solutions i.e. Vtn……..nth, where n is random vector);

Calculate the fitness function value (trial vector, P);

Compare the Vt and trial vector and select the one of them which is giving the best solution.

Update Vt;

Until the termination criteria are satisfied.

End.

• Fig.4.    Differential Evolution algorithm

In DE algorithm, different variations are classified into ‘DE/x/y/z’. In this notation x represents vector to be mutated can be randomly or best, y represents numbers of variance vectors are used and z represents crossover scheme, present different is ‘bin’. Using this notation in DE algorithm use basic DE strategy is used i.e. ‘DE/rand/1/bin’.

DE/rand/1: In this, indices are selected randomly, so mutation operator is totally based on the random nature of the indices.

^X„w,g = ^Xr 1,g + ^F.(^Xr2,g -^Xr3,g ) (2)

Where Xnew,g is new vector generated by the mutation operator. r1, r2, r3 is randomly generated indices and F is fiddle factor.

• V. Experimental Details, Results and Discussion

In this section, provides detail specifications of problem instances and the results found by best fit, random fit and Differential Evolution algorithm.

Data Generator:

Eight problem instances are randomly generated to compare the performance of algorithms. Random data generator program is written in C programming language.

Characteristics of instances

• 1.    For experimentation we assumed heterogeneous physical machines and virtual machines.

• 2.    The PM and VM attribute requirements were created as a maximum or minimum combination of different ranges uniformly distributed random numbers.

• 3.    Datasets contains combination of CPU intensive, memory intensive and bandwidth intensive virtual machines. the vm requirements were generated as a mix of different ranges of uniformly distributed random numbers as follows:

• 4.    Performance of evolutionary algorithms may vary with the problem size. Performance of Differential Evolution algorithm is tested on small instance with 20 virtual machines and large instance with 250 virtual machines.

<0.7-0.9, 0.1-0.3, 0.1-0.3> : 30-35% VMs

<0.1-0.3, 0.7-0.9, 0.1-0.3> : 30-30% VMs

<0.1-0.3, 0.1-0.3, 0.7-0.9> : 30-35% VMs

Price and Storn proposed DE/rand/1 mutation operator in DE framework. This operator is most widely used by many researchers. In this paper, performance of basic mutation operator is compared with two different mutation operators described in [39].

• 1)    DE/best/2: In this, indices are not selected randomly, the best index is selected from the population which is best individuals. So, mutation operator is not based on the random nature of the indices.

Xnew, g = Xbest + ^F•( ^Xr 1,g - ^Xr 2, g ) + ^F•( ^Xr3,g - ^Xr4,g )

Where X_best,g = is indicates the best individuals.

• 2)  DE/current-to-best/1: In this, indices are not

selected randomly, the best individuals are selected from the current population. So, the mutation operator is based on the current population to best individual’s nature of the indices.

X new, g

= X current, g

^{+ F}.( ^Xbesi - ^XcurreMg) ^{+ F}'( ^Xrl g - ^Xr3 g ) est        current,g                r ,g        r ,g

Differential Evolution algorithm with basic mutation operator, DE/rand/1, provides good solutions to VMP problem. Table 1 shows comparison of three different mutation operators of Differential Evolution algorithm for the virtual machine placement problem described in section III. The best results obtained in 10 runs are reported with respect to iterations. Differential Evolution algorithm with DE/Best/2 mutation operator gives better results and shows better convergence than other mutation operators.

Table 1. Convergence of Differential Evolution Algorithm with Different Mutation Operators

Iteration	DE/rand/1	DE/current-to-best/1	DE/Best/2
100	53	51	50
500	52	50	48
1000	51	49	47
2000	50	47	46
5000	49	46	45
10000	47	45	44
15000	46	45	43
20000	46	44	43

Figures in bold indicates best values.

Table 2. Results of Differential Evolution Algorithm with Different Mutation Operators

No. of VMs	Algorithm	PMs used	CPU wastage	Memory wastage	Bandwidth wastage
20	DE/best/2	3	867	47	393
	DE/current -to-best/1	4	717	181	649
	DE/rand/1	5	1155	1254	390
40	DE/best/2	8	1021	2615	420
	DE/current -to-best/1	8	1021	2615	420
	DE/rand/1	8	1400	3106	828
60	DE/best/2	11	1226	3668	1359
	DE/current -to-best/1	14	1513	2774	2163
	DE/rand/1	16	4059	2777	3201
80	DE/best/2	13	2685	602	1408
	DE/current -to-best/1	13	3945	1763	1796
	DE/rand/1	14	4722	2197	1876
100	DE/best/2	22	4350	5937	3907
	DE/current -to-best/1	23	5201	5201	3638
	DE/rand/1	24	3950	6708	3752
150	DE/best/2	30	5112	8937	4601
	DE/current -to-best/1	31	5475	6289	4526
	DE/rand/1	31	5526	8066	4502
200	DE/best/2	40	5717	8536	5378
	DE/current -to-best/1	41	7113	10070	6737
	DE/rand/1	42	6311	10993	6910
250	DE/best/2	47	9864	9179	5446
	DE/current -to-best/1	49	11931	10108	5806
	DE/rand/1	51	7960	10381	6737

Figures in bold indicates best values

Differential Evolution algorithm is tested on eight problem instances with virtual machines varying from 20 to 250. Table 2 shows comparison of three different mutation operators of Differential Evolution algorithm, where the best results in 10 runs are reported. The algorithms are executed up to 100 iterations. Table 2 presents number of physical machines required to fit given virtual machines, CPU wastage, memory wastage and bandwidth wastage. DE/best/2 mutation operator gives better results than other two operators for six instances with respect to number of physical machines used. Performance of DE/best/2 is same or similar to DE/current-to-best/1 mutation operator for problem instances with 40 and 80 VMs respectively. For most of instances, performance of DE/current-to-best/1 is better than DE/rand/1 mutation operator.

Table 3 shows comparison of Differential Evolution algorithms with basic operators and best fitted operator with best fit algorithm and random fit algorithm.

Evolution algorithm with DE/best/2 mutation operator minimizes the number of physical machines used and resource wastage viz. CPU, memory and bandwidth.

110 -.

100 -

80-

■ DE/best/2

• DE/rand/1

* Best fit

• Random fit

Table 3. Comparisons of Differential Evolution, Random fit, and Best fit Algorithm

No. of VMs	Algorithm	PMs used	CPU wastage	Memory wastage	Bandwidth wastage
20	DE/best/2	3	867	47	383
	DE/rand/1	5	1155	1254	390
	Best fit	7	1207	2290	876
	Random fit	10	3521	4678	1398
40	DE/best/2	8	1021	2615	420
	DE/rand/1	8	1400	3106	828
	Best fit	12	1861	3938	1452
	Random fit	20	6897	6044	4342
60	DE/best/2	11	1226	3668	1359
	DE/rand/1	16	4059	2777	3201
	Best fit	18	4193	2526	3270
	Random fit	25	9309	8367	5236
80	DE/best/2	13	2685	602	1408
	DE/rand/1	14	4722	2197	1876
	Best fit	21	7002	4028	3093
	Random fit	30	15230	9387	5589
100	DE/best/2	22	4350	5937	3907
	DE/rand/1	24	3950	6708	3752
	Best fit	28	4791	5911	4123
	Random fit	40	14304	15010	7861
150	DE/best/2	30	5112	8937	4601
	DE/rand/1	31	5526	8066	4502
	Best fit	39	6326	7668	6005
	Random fit	60	24108	23826	11608
200	DE/best/2	40	5717	8536	5378
	DE/rand/1	42	6311	10993	6910
	Best fit	55	8465	11880	9051
	Random fit	80	28840	32252	16749
250	DE/best/2	47	9864	9179	5446
	DE/rand/1	51	7960	10381	6737
	Best fit	64	10791	10618	7754
	Random fit	100	38540	40010	17665

Figures in bold indicates best values

	70-
	60-
г
L	50-
0
0 z	40-
	30-	* A
	20-
	10-	j i ■
	0-

■ 1 i 1 i 1 i 1 i 1 i 1 i 1 i 1 i 1 I 1 i 1 i 1 i 1

0   20 40 60 80 100 120 140 160 180 200 220 240 260

So. of VMs

Fig.5. Results of selected algorithms for VMP problem for 8 instances

40000-		• DE/best/2	Ж
35000 -		• DE/rand/1
		ж Best fit
30000 -		ж Random fit	ж
^ 25000 -			ж
I 20000-
a       ■
у 15000-	ж ж
10000 -	Ж А		А       i
5000 -	ж * I ♦ * i ■		1       1
	20 40 60 80 100		120 140 160 180 200 220 240 260

No. of VMs

Fig.6. Comparison of selected algorithms on CPU wastage level

45000 40000 35000 30000 - 5 25000 ' 20000 - о         1 Е 15000 - S 10000 - 5000 0-		• DE/best/2 • DE/rand/l * Best fit * First fit
	i	Ж ж ж ж          1 i 1 1 :

0 20 40 60 80 100

ж

20 140 160 160 200 220 240 260

.of VMs

Result from Table 2, Table 3 and Fig. 5 shows that Differential Evolution algorithm with all three mutation operator gives better results than best fit algorithm and random fit algorithm for all the eight instances of VMP. Fig. 6, Fig. 7 and Fig. 8 shows the comparison of selected algorithms with respect to resource wastage. Differential

Fig.7. Comparison of selected algorithms on memory wastage level

19000 ^

18000 -

17000 -

16000 -

15000 -

14000 -

13000 -

12000 -

11000 -

10000 -

9000 -

8000 -

7000 -

6000 -

5000 -

4000 -

3000 -

2000 -

1000 -

0-

• ■ DE/best/2                             ж

• • DE/rand/1

*  Best fit

*   First fit

:  }  '  1

20 40 60  80 100 120 140 160 180 200 220 240 260

No. of VMs

Fig.8. Comparison of selected algorithms on bandwidth wastage level

• VI. Conclusions

This paper presents virtual machine placement problem as constrained optimization problem. The objective is to minimize required number of physical machines to place all the virtual machines by satisfying resource constraints and with placement   guarantee.   Paper shows experimentation with Differential Evolution algorithms with three different mutation operators, best fit algorithm and random fit algorithm. Differential Evolution algorithm with selected three mutation operators give better results than best fit algorithm and random fit algorithm for all the eight problem instances. Results show that DE with DE/best/2 mutation operator gives better solutions and faster convergence than DE/current-to-best/1and DE/rand/1.