Диффузионный перенос в шарообразной грануле с идеальным контактом двух последовательных разнопроницаемых осесимметричных областей при граничных условиях первого рода

д т

r ² д r

дс 2 (r, т )_ D2 д

д т

r ² д r

дс1 (r, т) дr дс 2 (r,т) дr

Г , т >  0;

r , Т >  0;

с1 (r, 0) = с2 (r, 0) = c0 = const;(3)

с (rbт )=с2 (ri,т);

D     r"Т) = D 8с2 (r-Т> ;(5)

dr с2 (r2, т) = cs = const;(6)

q (0,т)*w,(7)

где τ – время; r – радиальная координата; r1,2 – радиусы областей; с1,2 и D1,2 – локальные концентрации и коэффициенты диффузии в грануле при 0 < r < r и r < r < r2 соответственно. Явные выражения с12 (r, т), полученные, как и в [6], методом интегрального преобразования Лапласа, тождественно удовлетворяют уравнениям системы и граничным условиям, однако начальные условия не выполняются, поэтому они справедливы для τ0.

В связи с этим целью исследования является решение системы (1)–(7), справедливое во всем диапазоне изменения τ и применение его для оценки кинетического параметра в постулате Глю-кауфа о скорости переноса однокомпонентной среды в линейной модели с сосредоточенными параметрами с учетом внутренней структуры гранулы.

Решение . Система (1)–(7) представлена в безразмерной форме:

d C 1 ( R , 6 ) _ d 6   =	1 d R 2 d R	"  2d C 1 ( R , 6 ) 1 R d R
d C 2 ( R , 6 ) =	D d	"R 2 d C 2 ( R , 6 ) "
d 6	' R 2 d R	d R

, 1 <  R <  п , в >  0;

0 <  R <  1, в >  0;

С ( R , 0 ) = С ₂ ( R , 0 ) = 1;

С ( 1, 6 ) = C 2 ( 1, 6 ) ;

дС1 (1,6 )  d dC2 (1,6 )

д R          d R   ’

C 2 ( П , 6 ) = 0;

С ( 0, 6 ) *«

с помощью относительных переменных:

6 = tDi/г? ; R = r/r ; D = D 2 /D. ;

С ₁₂ ( R , 6 ) = Г с ₁₂ ( r,т ) - c s ]Д c₀ - c s ) ; п = г ₂/ г 1 . Следуя адаптированному методу разделения переменных Фурье к подобным постановкам [7], структура решения (8) и (9) выбрана в виде

C 1,2 ( R,6 ) = ^ 1,2 ( R ) -Г ( 6 ) ,                                      (15)

где неизвестные функции Ф 1 ₂ ( R ) и Г ( 6 ) , как следует из (8)-(15), определяются соответственно

из решения краевой задачи: 1 d Г 7 d^1 (R) 1    7    , x _ R2---LLJ + ^2 ^ (R ) = 0 ;                        (16) R2 dR [    dR  J     1H D d Г 7 d^7 (R) 1   7   / x —— R2--2^^ + Ц 2^2 (R ) = 0;                       (17) R2 dR [      dR   J      2V ’ ^1 (1) = T 2 (1);                                            (18) dΨ 1dΨ 1 -4(2 = D —1^2 ;                          (19) dR       dR T 2 (n) = 0;                                          (20) T1 ( 0 )^^                                       (21) и задачи Коши

^(^ + ц 2Г( 6 ) = 0, dθ

r(0) =1,

где μ – собственные значения.

Общие решения (16), (17):

¥ 1 ( R ) = A 1 sin ( цR )/ R + B 1 cos ( цR )/ R;

¥ 2 ( R ) = A ₂ sin ( цК JD ) /r + B₂ cos ( цR/^Гl

причем в силу (21) B 1 = 0, а остальные константы интегрирования в соответствии с (18) - (20) должны удовлетворять матричному уравнению

[Л][ X Г =[0]г,

sin μ

• I ц — sin

I ц

— cos

[Л] =

- sin ц + ц cos ц

D

• I ц I ц        I ц I         I ц I , ц •( ц sin — —=cos -= cos -= + -= sin -=

,

1 • i цп i 1 i цп — sin I I —cos I —7^ п V '■Id ) п v Vd

[ X ] = [ A 1 ,A 2 ,B 2 ] ; [ 0 ] = [ 0,0,0 ] .

Собственные значения ц найдены из уравнения det [ Л ] = 0, которое имеет компонентный вид

,      1 I           . ц

1--sin ц+ —cos ц sin

D J     D

μ

--7= sin ц cos

(1 - п) -ц = 0.

Положив, например, A 1 = 1, из (26) определены остальные постоянные:

A 2 = sin ^ sin

+ -Ucos ^ cos I - ^ I ;

B 2 =

—

1          ■ ц L •        I ц

--^cos ц sin I —j= I+ sin ц cos I

Из (22), (23) следует, что Г(6) = exp(— ц26), и тогда где

z       ” Ф (R)

c,(R,6 )=Z п=1 Nn

η

J $ ² Т 1 ( $ ) d$ + J $ -р 2 ( $ ) d$ exp ( — ц П 6 ) , i = 1,2,

η

N n = J $ ² T 2 ( $ ) d$ + J $ ² T 2 ( $ ) d$ ,

μ _n – корни (27).

Детализация (30) с учетом (24), (25) и (28), (29) и выбором направления потока вещества

Q i ( R , 6 ) = 1 — q ( R , 6 )

позволила записать решение:

to

^Q 1 ( ^R , ⁶ ) = ^{1 —} E [ F ( ц п , ^D , п )^+ф( ц п , D , п ) ] ^sin ( ц п ^R ) • exp ( ^— ц 2 ⁶ )/ [ ^R ^ ( ц п , D , п ) ] ; n = 1

^

Q2 (R, 6 ) = 1 — ^[ F (цп, D, п ) + Ф( цп, D, п )] A2sin I ^ I +

п = 1

где

+ B 2 cos

F ( Ц п , D , n ) = — ^Ц п ^COSЦ n ^— sin ^Ц п + a ₂ μ _n

+ cos I ^Ц^ I ц _п D + dJd sin

^Ф( Ц п , ^D , n ) = B 2 ^sin I^ = I Ц п Dn ^{— sin} I^

Q( ^,D, n ) = -! Цп

—

1 cos ( 2 Цп ) + ( b22 —

— cos I ^ п ^- I ц _п nD +

cos

—

;

;

— 1V D sin I ^2ц1

2     I Dd

+ Ц п ( 1 — n ) — 2 A 2 B ; cos²

Анализ. Если ( 1 — n)/Do = p/q , где p, q - целые, то уравнение (27) имеет дополнительные корни Х_к = q n k, к = 1, го . Тем не менее, будем считать, что наступление такого события в практических расчетах маловероятно.

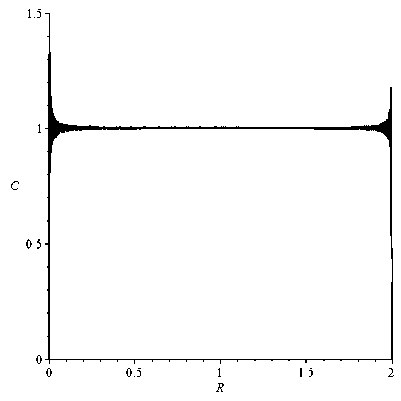
Рис. 1. Выполнение начальных условий при D = 3 и n = 2

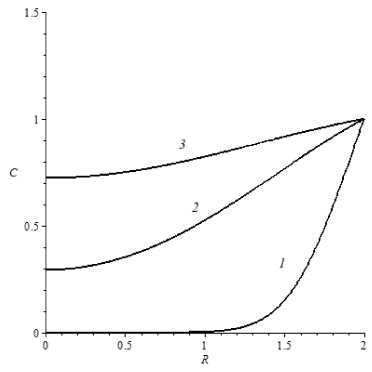
Рис. 2. Профили концентрации при D = 3 , n = 2 и различных θ : 1 – 0,05; 2 – 0,4; 3 – 0,8

Установлено, что начальные условия удовлетворены для любого набора D >  0 и n >  1 (в качестве примера рис. 1). Если D = 1 (однородный по проницаемости шар), то для любого значения П развитие профилей концентраций в одни и те же моменты времени остается одинаковым (рис. 2). При D <^ 1 проникновение вещества лимитируется проницаемостью области, примыкающей к поверхности гранулы (рис. 3, a ), а для D >  1 наоборот - лимитирует процесс поглощения область, находящаяся в ядре гранулы (рис. 3, b ). Следует заметить, что скорость процесса поглощения существенно выше при D >  1. Уменьшение радиуса контакта областей с разными проницаемостями уменьшает скорость поглощения вещества гранулой (рис. 3, c, d).

Воспользуемся полученным решением (32), (33) для оценки параметра к линейной модели массообмена с сосредоточенными параметрами d^ =K [■—Q (e)],

где Q (6 ) = -3 Qi (6) + 1

—

^^^“

K = kr ^² D

-3 Q 2 ( 6 ) ;    Q 1 ( 6 ) =

1 η

3 j R ² Q 1 ( R , 6 ) dR ;   Q 2 ( 6 ) = — J R ² Q 2 ( R , 6 ) ^R ;

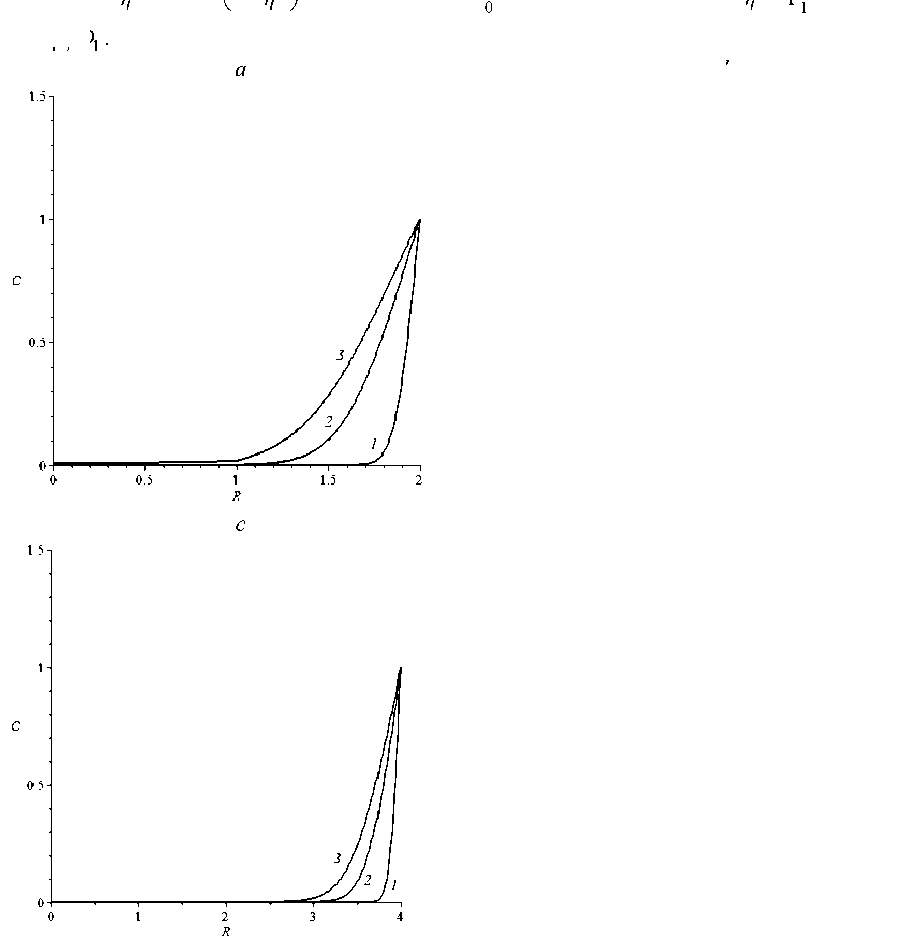
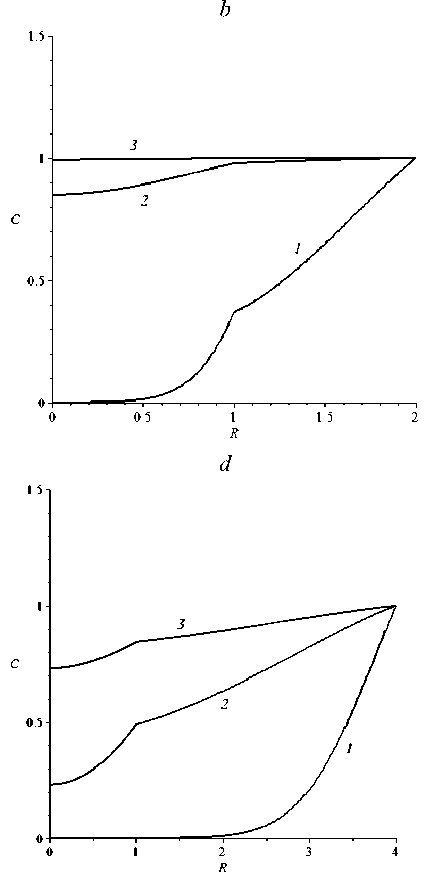
Рис. 3. Профили концентраций при: a - D = 0,1 , n = 2 ; b - D = 5 , n = 2 ; c - D = 0,1 , n = 4 ; d — D = 5 , n = 4 ;

и различных θ : 1 – 0,05; 2 – 0,4; 3 – 0,8

В выражении безразмерной среднеобъемной концентрации

■2  ”

Q (e ) = i—3^ E|

П  n=1[

M n cos M

n

—

M n

sin Цп .    A 2

mU

I ЦП I —Ц-nDn cos I —n= 1 +

⁺ 7 n D cos I "7=

B 2

72V

7 n Dn sin | ⁷ n | I — 7 n D sin I 4=1 +

> •

+

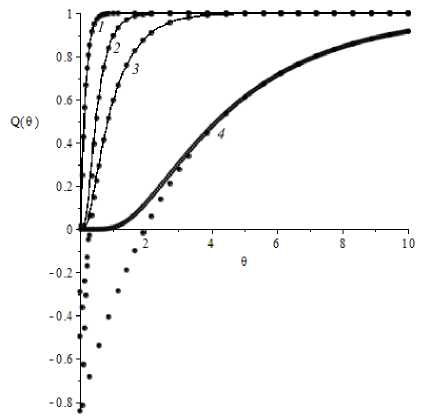
Рис. 4. Кинетика процесса поглощения вещества гранулой: 1 - D = 5 , п = 2 ; 2 — D = 5 , П = 4 ; 3 — D = 0,5 , п = 2 ; 4 — D = 0,5 , п = 4 (сплошные кривые – расчет по (35) с n = 200; • – расчет по (35) с n = 1)

можно ограничиться одним членом ряда (рис. 4), тогда из (34) и (35) при n = 1 следует, что

K = $ , откуда

k = ^ 12 п^D 1

^r 2 ²

.

В случае однородности гранулы по проницаемости ( D = 1 ) кинетический параметр равен [8]

- 1,

D = —D1 + пI

—

'

п3 >

, п 2 D kо =   2  , r22

D 2

– среднеобъемный коэф-

фициент диффузии. Расчет показывает, например, для D = 3 и п = 2 : к = 1,21, к 0 = 13,57 . Это означает, что допущение об однородности гранулы может вносить существенную погрешность в оценку скорости поглощения вещества без учета реальной структуры.

Заключение . Показано, что неучёт локальной неоднородности гранулы по проницаемости на основе диффузионного механизма переноса при оценке кинетического параметра линейной модели внутригранулярного массообмена в соответствии с постулатом Глюкауфа существенно завышает скорость поглощения среды, что, в свою очередь, может привести к замыканию массогабаритных характеристик аппаратов с зернистым материалом.