Дифракция электромагнитных волн на спиральных элементах

Спиральные элементы широко используются в СВЧ- и антенной технике в качестве самостоятельных антенн, в антенных решетках, как элементы облучателей зеркальных антенн, в замедляющих системах и других элементах СВЧ-устройств. Интенсивное исследование спиральных элементов как антенн началось еще в середине прошлого века, когда возникла необходимость в широкополосных излучателях с управляемой поляризацией [1]. Были построены математические модели с различной областью применения [2; 3]. Наиболее точными являются модели, построенные на основе интегральных уравнений (ИУ) [3–5].

В настоящее время возрос интерес к свойствам именно спиральных элементов. Это связано с появлением и развитием теории киральных структур [6] и, если говорить более обобщенно, теории метаматериалов. Метаматериалы создаются на основе внедрения в диэлектрик различных включений определенной конфигурации. Эти включения можно рассматривать как атомы либо молекулы чрезвычайно больших размеров. Расположение и конфигурация включений определяют электродинамические свойства метаматериала. К метаматериалам естественного происхождения позволим себе отнести ферриты, совершившие в свое время определенного образа революцию в СВЧ-технике, а также жидкие кристаллы (оптический диапазон), технологии на основе которых прочно вошли в нашу жизнь.

Как правило, исследование киральных сред осуществляется с помощью феноменологической теории, материальные уравнения которой имеют вид [7]

—* —* —* —* —* —*

D = б E + i X H, B = Ц H ± i X E . (1)

В данных выражениях верхние знаки соответствуют киральной среде на основе спиралей с правой закруткой, а нижние знаки – среде на основе левовинтовых спиралей. Константа χ называется параметром киральности. Достоинством исследования киральных структур с помощью феноменологических уравнений является относительная простота аналитических выводов. Но здесь следует отметить усредненный характер уравнений, необходимость знания параметра киральности и его частотной зависимости для конкретной среды, малость размеров кираль-ных элементов в сравнении с длиной волны и большое расстояние между элементами, позволяющее пренебречь их взаимодействием.

Таким образом, область применения феноменологических уравнений существенно ограничена. Кроме этого, можно утверждать, что ки-ральные свойства будут более ярко выражены в средах, построенных на основе элементов, соизмеримых с длиной волны.

Корректное описание элементов, соизмеримых с длиной волны, возможно только на основе строгого электродинамического подхода,

который избавляет от необходимости введения параметра киральности, снимает ограничения на размер элементов и расстояния между ними, а также дает корректное описание ближней зоны киральных элементов. Более того, строгий подход в принципе дает возможность перехода к феноменологическим уравнениям (1).

Основным недостатком строгого подхода можно считать сложность численных расчетов и аналитических выводов. С практической точки зрения спиральные элементы представляют интерес в качестве рассеивателей электромагнитного поля (ЭМП). Строгое решение задачи дифракции на спиральных элементах связано с такими важными задачами, как создание покрытий, снижающих радиолокационную видимость, поглощающих покрытий, концентраторов энергии электромагнитных волн (ЭМВ).

Далее рассмотрим решение задачи дифракции на спиральных элементах с помощью интегральных представлений электромагнитного поля (ИП ЭМП).

1.    Интегральные представления электромагнитного поля

Интегральные представления электромагнитного поля являются удобным инструментом для построения математических моделей и полного электродинамического анализа излучающих структур. Наиболее часто встречающиеся в литературе ИП ЭМП записываются в виде [8] —          —   — —  —

E = ^Wc ( k ² A + ∇(∇ ⋅ A ));

ik                                               (2)

—*      —*     —*

H = ∇ × A .

Здесь E, H - векторы напряженностей электрического и магнитного полей; Wc = µa / εa – волновое сопротивление среды; k = ω εaµa = = 2π / λ – волновое число, εa и µa – соответс- твенно абсолютная диэлектрическая и абсолют- ная магнитная проницаемости среды; ω – круговая частота; λ – длина волны;

A ( Г) =    — ( q ) G ( — , r ') dV

V ^—

– векторный электрический потенциал A в точке наблюдения p, создаваемыйобъемнойплотностью тока j; —(p) = r — радиус-вектор, проведенный в точку наблюдения; q – точка источника;

—(q) = —' — радиус-вектор, проведенный в точку источника. Интегрирование производится по точкам источника q, находящимся в объеме V. Выражение

* *     exp(- ikR ( ^— , r '))

G ( r , r ') =

4п R ( — , r ')

называется функцией Грина свободного пространства;

R ( r , r ') = r - r ‘|

– расстояние между точкой источника и точкой наблюдения.

В [9] приведено интегро-дифференциальное представление ЭМП, создаваемого электрическим током j , находящимся в объеме V :

——

E(—) = Wc   (j (q)k2 G(r, —') - ik v

——

- (V q ■ j ( q ))( r - — ') B ( r , r ')) dV ;                       (3)

j H ( — ) =   (( — - r ') _x — ( q )) в ( r , r ') dv ,

V где

_B =- ikR +1 _{G .} R ²

Данное представление полностью эквивалентно представлению (2), но не содержит дифференциальных операторов, применяющихся к точке наблюдения.

На основе выражений (3) в [9] получены ИП ЭМП тонкопроволочной структуры. ТПС представляет собой идеально проводящую беско-

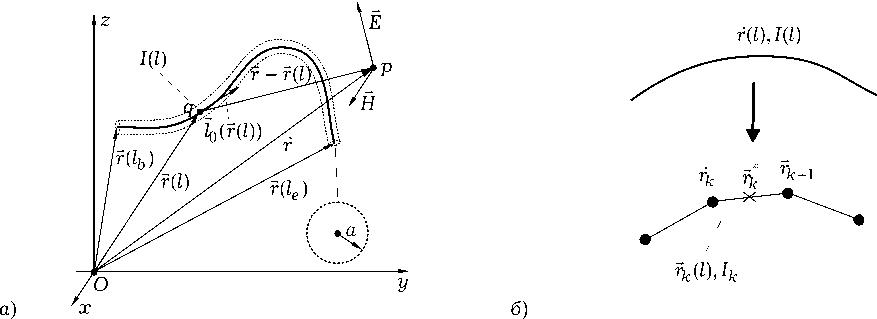
Рис. 1. Тонкопроволочная структура ( а ) и линеаризация ее образующей ( б )

нечно тонкую металлическую трубку радиуса a и длины L , произвольно расположенную в пространстве и не имеющую самопересечений (рис. 1, а ). Считается, что объемная плотность тока j, определенная лишь на образующей ТПС и возникающая под действием стороннего элек-

^—т ( in )

трического поля E , имеет только продольную составляющую, поэтому ее можно записать в виде

*

j ( q ) =

—

^I(—)§(r '- r(l)), 2n a здесь —о(—(l)) - единичный вектор касательной на образующей L, описывающейся радиус-вектором —(l); определяется как:

—о(—(— )) = dr®, l е [—ь , le ] - натуральный параметр на образующей (в дальнейшем l будем также называть продольной координатой, lb – координатой начала ТПС, le – координатой ее конца); I(l) – распределение тока по образующей; 5(ж) — дельтафункция. Также предполагается, что при любых значениях l радиус a много меньше радиуса кривизны р(l) = |dl0(l) / dl|.

На поверхности идеально проводящей трубки выполняются граничные условия для продольных компонент поля:

— о ( — ( l )) ■ ( E ⁽ in ) ( s ) + E ( s )) = 0.

Вектор E ⁽ in ) создается сторонними ЭМП различного рода, вектор E — объемной плотностью тока на структуре. Данное условие можно ослабить, требуя выполнения граничного условия не на поверхности трубки, а на ее образующей:

—)( r ( — )) ■ ( E ⁽ in ) ( r ( l )) + E ( r ( l ))) = 0.                        (4)

В [9] получено интегральное представление ЭМП от тока I ( l ), протекающего по образующей

L ТПС:

F ( r ) =    I ( l ') K F ( — , r ( l )) dl ',    F = E , H .             (5)

L

Здесь

K E ( r , — ( l )) = Wp | * о (l')k ² G a ( r , — ( l ')) + ik ^

+    (( — - r ( l ')) B a ( — , r ( l ')))l;

d l                          )

K H ( r , r ( l )) = (( r - r ( l ')) X — ) ( l ')) B a ( — , r ( l ')),

– ядра интегральных представлений;

F a ( — , r ( l ')) = F ( R a ( r , r ( l '))), F = G , B

R a ( r , — ( l ')) = Vl — - r ( l ')|² + a O'

– регуляризированное расстояние между точкой источника и точкой наблюдения; в качестве параметра регуляризации выступает радиус a провода. В случае подстановки граничного условия (4) в (5) при F = E получается известное интегральное уравнение для определения тока произвольной тонкопроволочной структуры, приведенное, например, в [3].

При численном моделировании гораздо удобнее работать с дискретными моделями, поэтому осуществим дискретизацию интегральных представлений (5).

Пусть r ( l ) — радиус-вектор образующей ТПС, l е [ —ь , l e ]; L = l e - —ь — длина образующей. Разобьем образующую на сегменты длиной А (рис. 1, б ). Если число сегментов равно N_s , то А = L / ( N_s + 1). Введем индексы:

k = 1,..., N_s ;    к ' = 1,_, N_s +1.

В данных обозначениях —к' = А(к' -1) — значения натурального параметра на границе к -1 и к-го сегментов, — - = — (—к -) — соответствующий радиус-вектор, —к = —к + А /2 — значение натурального параметра в центре k-го сегмента, ——* = — (—к) — соответствующий радиус-вектор. Осуществляя линеаризацию образующей, уравнение сегмента можно записать следующим об- разом:

— ( — ) = — + — о к — ; — е [ — к -А /2, — к +А /2],       (6)

здесь:

* * ^+1 ⁺ r ^. ^—      Т к +1 ^{- —} к

— с ="-----; ^l 0 к =-----; -----.

2А

Далее, полагая, что А ^ X, будем считать распределение тока на каждом сегменте равномерным:

I ( — ) = I k ; — е [ — к -А /2, — к +А /2].

Подставляя данное выражение и выражение (6) в интегральное представление (5), получаем дискретизированное интегральное представление ЭМП:

N _s

F ( — ) = 2 I k K А’ ^F ( — , — ), f = e , н ;              (7)

к = 1

здесь:

— к +А /2

К А , ^F ( — , — ) = J K F ( r , r k ( — )) d— , F = E , н

— к -А /2

– весовые коэффициенты.

В дальнейшем дискретизированные ИП будем

– компоненты ядер;

записывать в компактном виде:

F(r) = F ^ ( r; r k , I k ); F = E , H , (8) где явно указываются параметры представления — координаты границ сегментов k , значения тока I k на сегментах, а также длина сегмента А и радиус провода a .

2.    Интегральное представление поля и система интегральных уравнений

Для упрощения дальнейших выводов будем записывать ИП (5) в компактной форме: *                   *

F ( r) = F a ( — ; r( l ), I ), F = E , H ,                      (9)

где явно указываются параметры представления – распределение тока I , образующая ТП-структуры r ( l ) и радиус провода a . В дальнейшем индекс a при отсутствии в нем необходимости будем опускать.

Выражение (9) описывает ЭМП одиночной ТПС. Как правило, мы имеем дело с некоторой совокупностью N тонкопроволочных элементов:

L : L1, L2, — LN, где Li – образующая i-го элемента, описывающаяся радиус-вектором:

ri (l) = a Xi (l) + У0 Y (l) + —0 Zi (l), l e [0; Li ], i = 1,- N, здесь Xi (l), Yi (l), Zi (l) – некоторые гладкие функции, зависящие от натурального параметра l; i – номер тонкопроволочного элемента; Li – длина i-й образующей.

Полное ЭМП такой структуры находится с помощью интегрального представления (9) с учетом принципа суперпозиции:

F ( — ) = Y F ( — ; r , I i ); F = E , H ,                (10)

i

Таким образом, (10) представляет собой ИП ЭМП сложной тонкопроволочной структуры.

В ИП (10) входят неизвестные пока токи I_i . Для их определения используем граничное условие (4) на каждом проводнике структуры. В результате получим систему интегральных уравнений следующего вида:

——    —    —

• - Z g ( r ) ■ E ⁽ in ) ( — ) = l 0 ( — ) - Y E ( r ; — , I i );

i                            (11)

• r = — ; i , j = 1,-, N .

Данную систему можно классифицировать как систему ИУ Фредгольма первого рода [10]. Решение подобных ИУ является некорректной математической задачей, т. е. оно может быть неустойчивым. Существует множество методов решения, обладающих определенными регу- ляризирующими свойствами. Асимптотическая корректность и регуляризирующие свойства некоторых методов рассмотрены в [11]. Наиболее простым и естественным является метод сшивания в дискретных точках [12].

Введем дополнительные обозначения. Пусть Ii k – значение амплитуды тока на ki -м сегмен-,i те i-го элемента, k = 1, —, Nv, где N^- — число ss сегментов i-го элемента; Аi — длина сегментов i-го элемента; ai – радиус провода i-го элемента; ri к. — радиус-вектор, проведенный в точку сопряжения ki и ki + 1 -го сегмента i-го элемента. Тогда по аналогии с (10) на основе дискретизированных ИП (8) можно записать:

N N si

F ( — ) = YY F A i ( r ; r i , k. , I i , k. ), F = E , H .      (12)

i    ⁱⁱ

• i = 1 k i = 1

Выражение (12) описывает ЭМП, создаваемое совокупностью N излучающих элементов с сегментированными образующими.

Для использования (12) необходимо знать неизвестные амплитуды токов I_{i , k} . В рамках метода сшивания в дискретных точках потребуем выполнения граничного условия типа (4) в центрах сегментов. Пусть r j , _k. — радиус-вектор, проведенный в центр k_j -го сегмента j -го элемента. Тогда из (12) с учетом учетом граничного условия (4) получаем систему линейных алгебраических уравнений для определения I_{i k} : , _i

N N si

• -10(r) ■ E⁽in)(r) = l0(r) ■ Y Y EAi(r;r,k.,Ii,k.);

3.    Геометрия исследуемых спиральных элементов

i = 1 k i = 1 i                  (13)

r = — * kj , j = 1,-, N , k j = 1,_, N sj .

Устойчивое решение достигается при соблюдении условия A i ^ 4 a i для всех i [11].

Геометрия исследуемых спиральных элементов представлена на рис. 2.

Уравнение образующей цилиндрической спирали в ненатуральном параметре записывается следующим образом:

r ( t ) = a cos ta * 0 + a sin tf — 0 + htz 0 , здесь a — радиус спирали, h ^ 0 — коэффициент намотки. Если h > 0, то спираль будет правовинтовой, если h <0 — левовинтовой.

Натуральный параметр на ПСА определяется как интеграл:

t l (t) = J |—"(t ')| dt' = V h2 + a21,

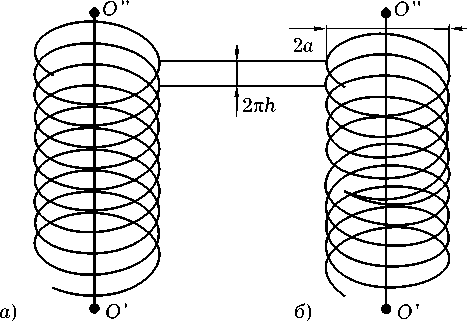
Рис. 2. Геометрия спиральных элементов: а ) цилиндрическая спираль; б ) совмещение лево- и правовинтовых спиралей

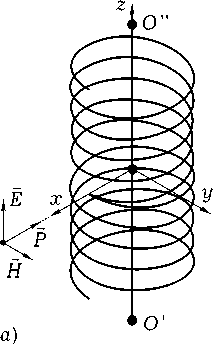
Рис. 3. Падение плоской линейно поляризованной электромагнитной волны на спиральный элемент: а ) вертикальная поляризация; б ) горизонтальная поляризация

где

—*

l ( t ) =

dr ( t ) dt

- a sin ta + a cos tf — o + hz o ,

– касательный вектор к образующей. Таким образом, в натуральном параметре уравнение образующей спирали будет иметь следующий вид:

r ( l ) = a cos(^ l ) a * о + a sin(^ l ) f — ₀ + h^ l ^— o , l e [- L /2; L /2].

Здесь £ = 1 / V a ² + h ² ; L — длина провода спирали. Если задавать число витков спирали N_l , то L = 2nN l / ^.

Образующие структуры, состоящей из право-и левовинтовой спирали, описываются выражениями:

Г 1(2) ( l ) = a cos(^ l ) 3 0 + a sin^ l ) f o ± h^l ^— 0 , l e [0; L /2].

Верхний знак соответствует правовинтовой спирали ? i ( l ), нижний знак — левовинтовой спирали r 2 (l ). В дальнейшем цилиндрическую спираль, образующая которой описывается выражением (14), будем называть обычной спиралью, а структуру, представленную совмещением лево- и правовинтовых цилиндрических спиралей, образующие которых описываются выражением (15), – совмещенной спиралью. Определение неизвестных токов для конкретной структуры осуществляется с помощью СЛАУ, получающегося в результате подстановки (14) либо (15) в (13) c учетом (6). После определения токов из полученной СЛАУ расчет ЭМП производится с помощью (12) при подстановке в него (14) либо (15) c учетом (6).

Под осью спирали будем понимать линию, совпадающую с осью Oz ( O'O" — отрезок, лежащий на оси спирали, рис. 2).

4.    Результаты численного моделирования

Возбуждение структур осуществлялось плоской линейно поляризованной электромагнитной волной (ПЭМВ), электрический вектор которой можно записать следующим образом:

E(in)(— = poeо exp(-ikr + y), где k = kok — волновой вектор; k—o — единичный волновой вектор; k – волновое число; E0 – амплитуда волны; po — единичный вектор поляризации; у — начальная фаза. Преполагалось, что Eo = 1 В/м, у = 0.

Параметры структур:

• •    отношение коэффициента намотки к радиусу спирали h / a = 2/30;

• •    радиус провода б / h = 1/10;

• •    число витков N l =10 (5 + 5 для совмещенной спирали);

• •    число сегментов N s = 500 (250 + 250 для совмещенной спирали).

Исследования проводились для различных соотношений a / к.

Наиболее интересным, на наш взгляд, являлось сравнительное исследование распределений токов и соответствующих им диаграмм рассеяния (ДР) в случае возбуждения спиральных элементов вертикально поляризованной ПЭМВ, т. е. p o = ^— o , падающей против оси Oa ( k — o = - a ^). Результаты численного моделирования для различных соотношений a / к представлены на рис. 4–7. Видно, что, несмотря на большую геометрическую схожесть структур, соответствующие распределения тока и диаграммы рассеяния кардинально отличаются. Так, при a = 0.1к совмещенная спираль имеет два максимума в ДР,

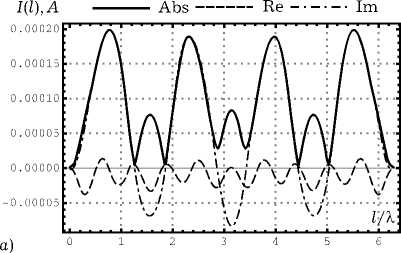
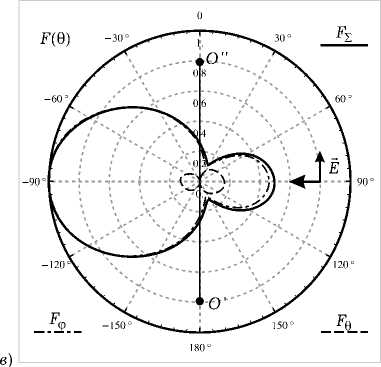
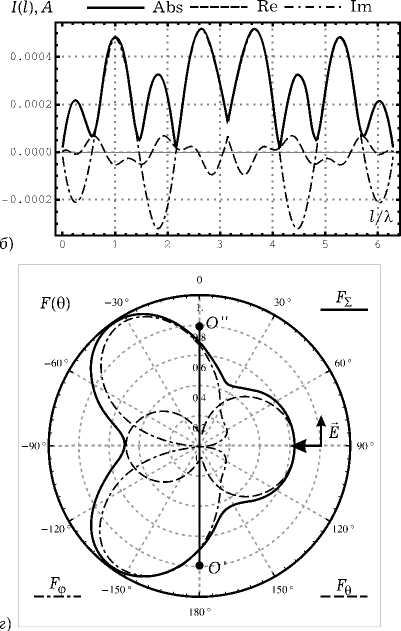
Рис. 4. Результаты численного моделирования для вертикально поляризованной ПЭМВ при a = 0.1 Х : а ) распределение тока на спирали; б ) распрелеление тока на совмещенной спирали; в ) нормированная диаграмма рассеяния для спирали в угломестной плоскости при ф = 0; г ) нормированная диаграмма рассеяния для совмещенной спирали в угломестной плоскости при ф = 0

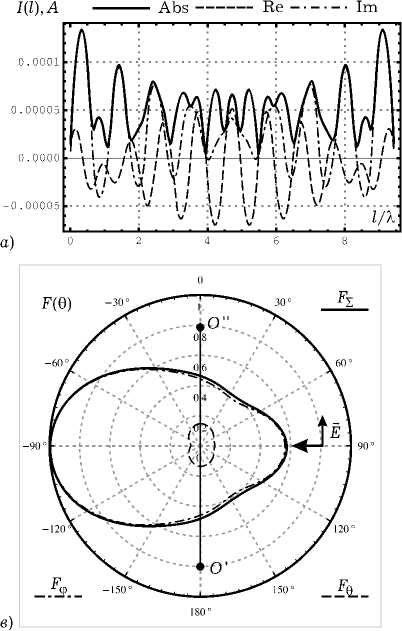
Рис. 5. Результаты численного моделирования для вертикально поляризованной ПЭМВ при a = 0.15 Х : а ) распределение тока на спирали; б ) распрелеление тока на совмещенной спирали; в ) нормированная диаграмма рассеяния для спирали в угломестной плоскости при ф = 0; г ) нормированная диаграмма рассеяния для совмещенной спирали в угломестной плоскости при ф = 0

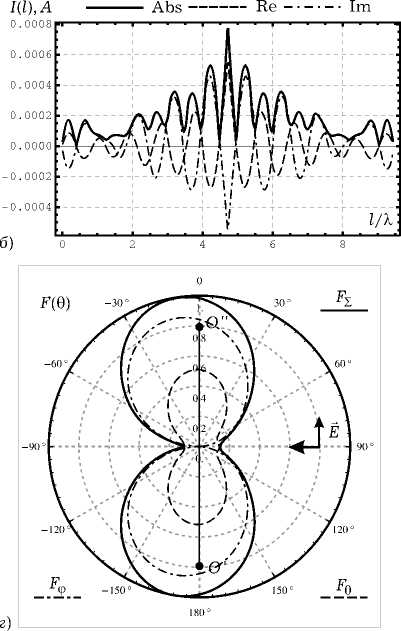
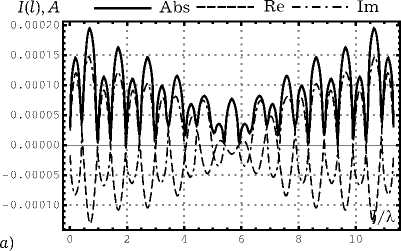
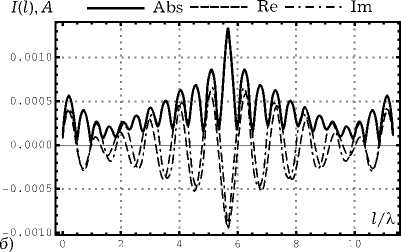
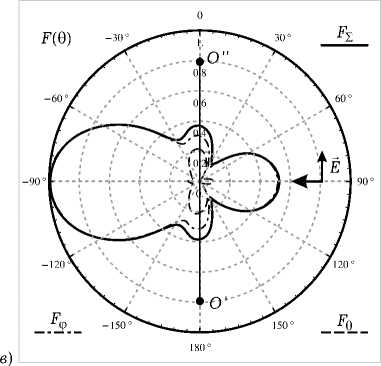
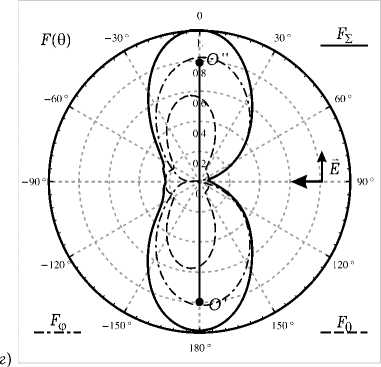
Рис. 6. Результаты численного моделирования для вертикально поляризованной ПЭМВ при a = 0.18 Х : а ) распределение тока на спирали; б ) распрелеление тока на совмещенной спирали; в ) нормированная диаграмма рассеяния для спирали в угломестной плоскости при ф = 0; г ) нормированная диаграмма рассеяния для совмещенной спирали в угломестной плоскости при ф = 0

Щ^А ----- Abs------Re------Im Щ),А ----- Abs------Re------Im

0.00020 0.00015 0.00010 0.00005 0.00000 -0.00005 -0.00010 -0.00015

a) °        ^{2        4        6        8       10}       -2       6)         0        2        4        6        8       10       12

г)

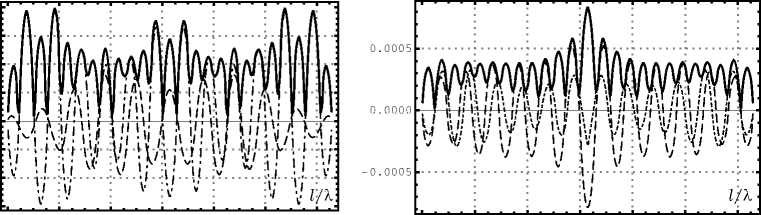
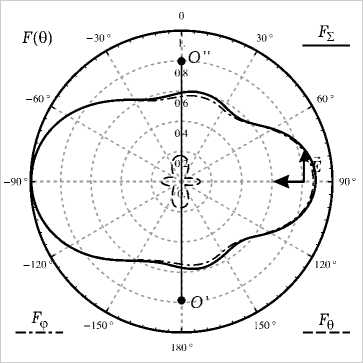
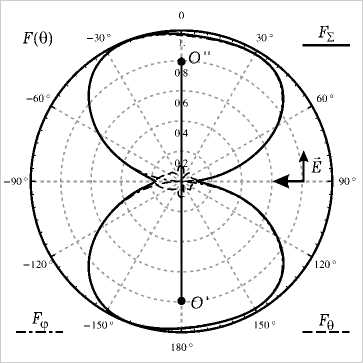
Рис. 7. Результаты численного моделирования для вертикально поляризованной ПЭМВ при a = 0.2 Х : а ) распределение тока на спирали; б ) распрелеление тока на совмещенной спирали; в ) нормированная диаграмма рассеяния для спирали в угломестной плоскости при ф = 0; г ) нормированная диаграмма рассеяния для совмещенной спирали в угломестной плоскости при ф = 0

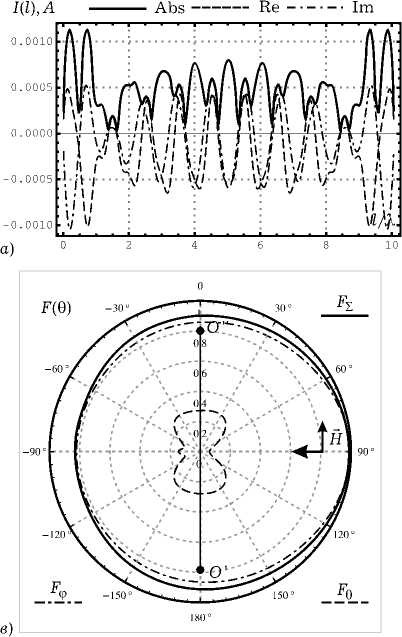
Рис. 8. Результаты ч и сленного моделирования дл я горизонта л ьно поляризованной ПЭМВ при a = 0.16 Х : а ) распределение тока на спирали; б ) распрелеление тока на совмещенной спирали; в ) нормированная диаграмма рассеяния для спирали в угломестной плоскости при ф = 0; г ) нормированная диаграмма рассеяния для совмещенной спирали в угломестной плоскости при ф = 0

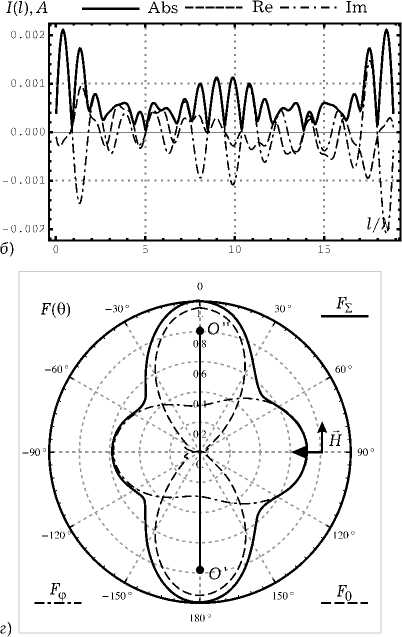
которые образуют примерно 30 градусов с направлением распространения ПЭМВ, а ДР обычной спирали имеет один максимум, совпадающий с направлением распространения ПЭМВ. Распределение тока на совмещенной спирали имеет много сходства с распределениями, возникающими в случае возбуждения структуры генератором ЭДС, расположенны в точке, которой соответствует l = 0 (здесь возникают заряды разных знаков).

Далее на рис. 5 видно, что максимумы в ДР для совмещенной спирали практически ортогональны направлению распространения ПЭМВ, а распределение тока имеет характер смешанной волны, распространяющейся и затухающей к концам спирали. У обычной спирали вблизи концов в распределении тока находятся максимумы. На рис. 6–7 характер распределений сохраняется, но происходит расширение главных лепестков в ДР.

Таким образом, совмещенная спираль представляется нам интересным элементом, рассеивающем электромагнитные волны в осевом направлении в довольно широкой полосе частот. К сожалению, подобного эффекта в случае падения ПЭМВ с горизонтальной поляризацией обнаружено не было. Максимумы в осевом направлении наблюдаются только при a = 0.16Х, т. е. вблизи резонансной длины колец 2пa ® 1, и выражены довольно слабо (рис. 8).

Заключение

В статье представлены решения задачи дифракции на спиральных элементах и приведены сравнительные результаты численного моделирования в случае возбуждения плоской электромагнитной волной вертикальной либо горизонтальной поляризации, падающей ортогонально к оси структур. Результаты моделирования являются, на наш взгляд, достаточно интересными. Так, несмотря на большую схожесть геометрии, структуры совершенно по-разному реагируют на падающую волну.

Важным представляется тот момент, что совмещенная спираль рассеивает ПЭМВ в направлении, перпендикулярном направлению ее распространения, причем данный эффект наблюдается в довольно широкой полосе частот. Это обстоятельство можно использовать при создании структур, рассеивающих и поглощающих электромагнитные волны, а также для создания концентраторов электромагнитной энергии.

С другой стороны, можно утверждать, что представленная модель может служить достаточно хорошим описанием совмещения слоев с различным знаком параметра киральности, т. к. взаимодействие между спиральными элементами в случае рассеяния вдоль оси будет слабым.