Дифракция плоской электромагнитной волны на градиентном диэлектрическом цилиндре

Для таких градиентных оптических элементов со сферической и поперечной цилиндрической симметрией, как линзы Лунеберга и Итона-Липмана известны аналитические выражения для зависимостей показателя преломления от радиальной координаты. Ход лучей в этих линзах изучен достаточно хорошо. В данной работе рассматривается прохождение электромагнитной волны через эти градиентные оптические элементы, в случае, когда радиус линз совпадает (или близок) с длиной волны. В таком резонансном случае лучевое описание дифракции света теряет силу и возникает вопрос о степени изменения фокусирующих и отражающих свойств данных градиентных элементов.

В данной работе развит аналитический метод расчета полей дифракции с ТЕ- и ТМ-поляризациями в случае падения плоской электромагнитной волны на неоднородный диэлектрический бесконечный круглый цилиндр, образующая которого вытянута вдоль оси z, а плоскость ( x, у ) совпадает с плоскостью падения. Неоднородность цилиндра аппроксимируется кусочно-постоянной функцией, а круговое сечение цилиндра при этом будет иметь N концентрических колец с постоянными значениями показателя преломления внутри каждого кольца (рис. 1). Метод основан на разложении проекции на ось z векторов напряженностей электрического (для ТЕ-поляризации) или магнитного (для ТМ-поляризации) полей внутри каждого однородного кольца в ряд по цилиндрическим функциям с неопределенными коэффициентами. Сами коэффициенты находятся из граничных условий, накладываемых на поля, и их радиальные производные на линиях скачков показателя преломления.

Заметим, что для анализа дифракции электромагнитной волны на градиентных цилиндрических оптических элементах, показатель преломления которых не обладает поперечной цилиндрической симметрией, можно использовать метод конечных элементов, разработанный в [6].

Дифракция плоской волны на N-слойном диэлектрическом цилиндре с круглым сечением

На рис. 1 показано схематично сечение круглого N-слойного цилиндра, в каждом слое которого показатель преломления имеет постоянное значение. Образующая данного бесконечного цилиндра вытянута вдоль оси z , плоскость падения плоской монохроматической электромагнитной волны совпадает с плоскостью (x, y).

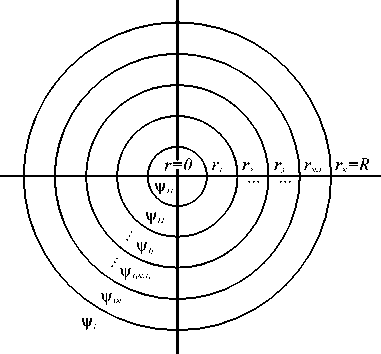
Рис. 1. Многослойный диэлектрический цилиндр

Для решения задачи требуется решить уравнение Гельмгольца для проекций Е z и H z . Если поместить центр системы координат ( x, у ) в центр круглого сечения цилиндра, то задачу можно решать в цилиндрических координатах ( r, ф ) : x = r cos ф , у = r sin ф . Известно, что частными решениями уравнения Гельмгольца в цилиндрических координатах являются цилиндрические функции, поэтому любое решение уравнения Гельмгольца в области переменных ( r, ф ) , где показатель преломления имеет постоянное значение, можно представить как линейную комбинацию независимых цилиндрических функций.

ТЕ-поляризация

В этом разделе введем обозначение E z = ψ .

Амплитуда поля во внутреннем круге (0 <  r <  r 1 ) представляется в виде ряда из функций Бесселя:

V 11 =

Z C 1 m J m ^k 4^ 1 ^r ) cos m V -

m =-v

Поле внутри j -го кольца диэлектрика представляется в виде ряда из функций Бесселя и Неймана:

V1 j =

= Z ^[ C ( 2 j - 2 ) m J m ^{( k} 4^ 3 r ^{)+ C} ( 2 j - 1 ) m ^Y m ^{( k} 4^ r l l co m ^V m =-v

Здесь считаем, что в свободном пространстве диэлектрическая проницаемость равна единице: ε₂ = 1.

В уравнении (3) у ₀ = exp( - ikx ) = exp( - ikr cos v ) – амплитуда падающей плоской волны с единичной интенсивностью.

Для нахождения неизвестных коэффициентов в рядах (1)-(3) используются граничные условия. Приравнивая сами поля и их радиальные производные на радиусах скачков показателя преломления r_j , получим систему уравнений:

^vj_r. = ^y i ( j + i )L r_j                    r_j

' aV1j    _ 8 V1(j+1)

j = 1, N - 1,

r j - 1 <  r <  r j , ^j = 2, N .

8r         8 r rj                        rj

Здесь r_N = R .

Амплитуда поля вне диэлектрика представляется в виде ряда из функций Ханкеля второго рода, так как они удовлетворяют условию излучения Зоммерфельда:

+”

V 2 = V 0 ⁺ Z C 2 Nm H m ^{( kr} ) cos m V , ^r >  R . ⁽³⁾ m =-v

V 1 n|r = V 2I R

8у 1 _N   _ 8 y ₂   , ^{( r} N = ^R ).

⁸ r   r    8 r   r

При j = 1 с учетом (1) и (2) из системы (4)

имеем:

Z C 1 m J m ^{( k}4^r 1 ^{) c0S} m V = Z [ C 2 m J m ^{( k}4^ 2 ^r 1 ^{) +} C 3 m ^Y m ^{( k}4^ 2 ^r 1 Jc ^Os m V m =-ю                        m =-v

4^ 1 Z C 1 m^J' m ^{( k} 4^ ^r 1 ^{) c0S} m V = 4 ^2 Z^[ C 2 m J' m ^{( k} 4^ 2 ^r 1 ^{) +} C 3 m^Y' m ^{( k} 4^ 2 r 1 j | ^C0S m V m =-rc                                     m =-rc

При j = 2, N - 1 с учетом (2) из системы (4) имеем:

+т

Z [C (2 j - 2) m J m m=-ro

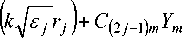
+rn г

= Z [ C 2jm J m

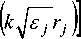
cos m v =

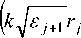
I + C ( 2 j + 1 ) m Y m

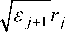
cos m V

m =-ro

+^

V ^ j ^{Z [} C ( 2 j - 2 ) m^J'm ^{( k}4^ j ^r j ^{) +} C ( 2 j - 1 ) m m =-rc

Y'_m ( k.^jr j ) ] cos m V =

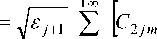
m (k V^ j+1 rj m=-rc

I + C ( 2 j + 1 ) m

m ( k V ^ j + 1 r j

cos m V

При j = N с учетом (2) и (3) из системы (4) имеем:

Z ^[ C ( 2 N - 2 ) m ^J m ^{( k} 4^ N ^r N ^{) +} C ( 2 N - 1 ) m ^Y m ^{( k} 4^ N r N jc^ m V = ^m =^-to

IV+^

• =    Z(- i ) mJm (krN )cos mV + Z C 2 NmHm2)( krN )cOs mV m=-v

  
  

4^ N Z ^[ c ( 2 N - 2 ) m^J'm ^{( k} 4^ N ^r N ^{) +} C ( 2 N - 1 ) m^Y'm ^{( k} 4^ N ^r N jc^ mV = m =-v

+v+v

• =    Z(- i ) mJ' m (krN )cos mV + Z C 2 NmH m (krN )cOs mV m=-v

Таким образом, системы (5), (6), (7) образуют одну общую систему из 2 N уравнений относительно неизвестных коэффициентов C_k , k = 1,2 N , где N - число однородных колец (или слоев) цилиндра (рис. 1).

Система уравнений решается для всех m -х коэффициентов разложения в ряды по цилиндрическим функциям (1)-(3). Полученные коэффициенты подставляются затем в уравнения (1)- (3).

ТМ-поляризация

Решение задачи дифракции плоской ТМ-поляризованной электромагнитной волны на многослойном диэлектрическом цилиндре аналогично решению в случае ТЕ-поляризации, который был рассмотрен в предыдущем разделе. Главным отличием этой задачи от случая ТЕ-поляризации является другой вид граничных условий:

W ij\ _rj = V 1 ( j ₊ 1 )|

r j

I ^dV 1j    _ 1 ^d V 1 ( j + i )

£j   8 r r    £j+i    8 r rj

V i n L ^_ V 2I r

*   1 ^d V i n

£ n  S r

d v 2

j _ 1, N - 1,

, ^{( Г} N ^_ R )-

Здесь введено обозначение H z _ v -

И в случае ТЕ-поляризации, и в случае ТМ-поляризации матрицы полученных систем линейных алгебраических уравнений имеют одинаковую структуру. В [7] для решения системы предложен метод прогонки, дающий необходимые рекуррентные соотношения для поиска неизвестных коэффициентов.

Численные примеры

Рассмотрим дифракцию плоской ТЕ-поляризованной электромагнитной волны с длиной Л _ 1 мкм на диэлектрическом цилиндре единичного радиуса R _ 1 мкм, чей показатель преломления зависит от радиуса следующим образом (внутренняя линза Лунеберга) [2]:

₂      1 + r ² - г ²

n 2 (г)_----4----, Г1 < 1, r12

где r 1 – расстояние от центра цилиндра до точки геометрического фокуса. В качестве примера возьмем г ₁ _ 0-75 мкм. Выберем число слоев цилиндра равное 10, а максимальный порядок аппроксимирующих цилиндрических функций в рядах (1)-(3) – 20.

Распределение амплитуды проекции вектора напряженности электрического поля показано на рис. 2.

Общий размер картины дифракции – 4х4 мкм (рис. 2а). Количество отсчетов сетки дискретизации – 300х300 пикселов. Величина фокусного расстояния r₁ , рассчитанная при помощи выше изложенного метода, составила г « 0,787 мкм. Относительная погрешность по сравнению с заданным значением r 1 равняется ® 4,9%. Здесь следует отметить, что рассчитанное значение r₁ сравнивается со значением, полученным при лучевом приближении.

Рассмотрим задачу с теми же параметрами, но для случая ТМ-поляризованной падающей плоской волны.

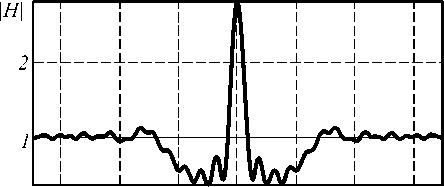
Распределение амплитуды напряженности магнитного поля показано на рис. 3.

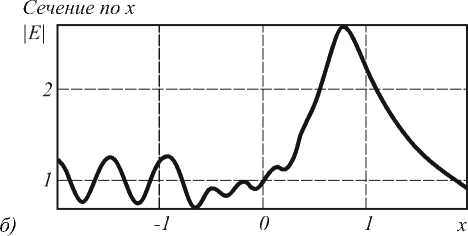
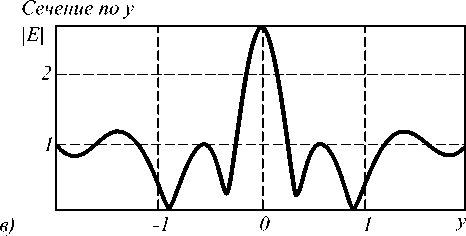
Рис. 2. Распределение амплитуды напряженности электрической поля: а) 2D распределение; б) сечение по оси Х (горизонтальная ось) через фокус; в) сечение по оси Y (вертикальная ось) через фокус

Величина фокусного расстояния r 1 составила г « 0,653 мкм. Относительное отклонение рассчитанного фокусного расстояния от заданного значения г 1 равняется ® 12,9 %.

Рассмотрим случай, когда г ₁ >  1. Показатель преломления обобщенной линзы Лунеберга запишется в виде [3]:

n ( г ) _ exp

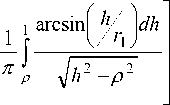
, р _ n ( г ) г ,

0 < р < 1.

Трансцендентное уравнение (10) относительно n ( г ) решалось численно, так как интеграл в (10) не берется в элементарных функциях. Пусть на диэлектрический цилиндр падает плоская ТЕ-поляризованная электромагнитная волна с длиной волны X _ 0,2 мкм. Выберем фокусное расстояние равное г₁ _ 2,55 мкм, радиус линзы - R _ 1 мкм. Определим число слоев цилиндра равное ста, а максимальный порядок аппроксимирующих цилиндрических функций – 35.

в)

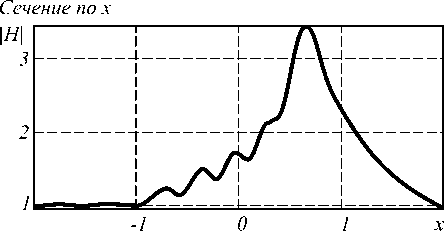
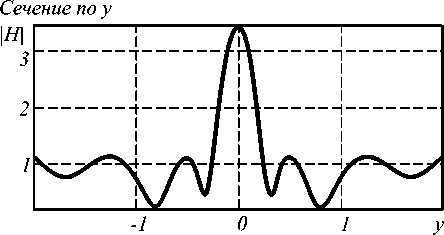
Рис. 3. Распределение амплитуды напряженности магнитного поля: а) 2D распределение; б) сечение по оси Х (горизонтальная ось) через фокус;

в) сечение по оси Y (вертикальная ось) через фокус

Распределение амплитуды напряженности электрического поля показано на рис. 4.

Общий размер картины дифракции – 7х7 мкм. Количество отсчетов сетки дискретизации – 300х300. Величина фокусного расстояния r 1 , рассчитанная при помощи выше изложенного метода, составила r 1 ® 2,45 мкм. Относительная погрешность по сравнению с заданным значением r 1 равняется ≈ 3,9%.

Рассмотрим тот же случай, но для ТМ-поляризованной плоской электромагнитной волны.

Распределение амплитуды напряженности магнитного поля показано на рис. 5.

Общий размер картины дифракции – 7х7 мкм. Количество отсчетов сетки дискретизации – 300х300. Величина фокусного расстояния r 1 , полученная при помощи выше изложенного метода, составила r₁ ≈ 2,473мкм. Относительная погрешность по сравнению с предписанным значением r₁ равняется ≈ 3 %.

Во всех перечисленных случаях зависимость показателя преломления от радиуса монотонно спадала от центра круга до его поверхности (на расстоянии 1 мкм от центра показатель преломления был равен 1). В случае обобщенной линзы Лунеберга (10) показатель преломления в центре круга n ≈ 1,134, для внутренней линзы Лунеберга n ≈ 2,236.

Поэтому на рис. 2-5 почти нет френелевского отражения от рассмотренных градиентных линз Лу- неберга. Заметим, что для ТМ-поляризации (рис. 3) отражение назад много меньше, чем для случая ТЕ-поляризации (рис. 2).

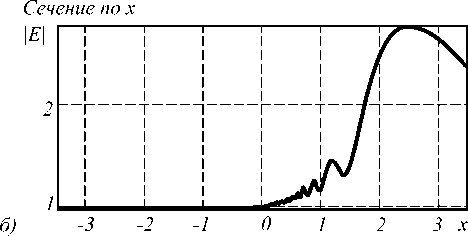
Сечение по у

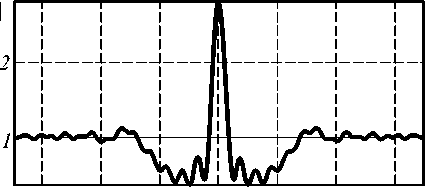
Рис. 4. Распределение амплитуды напряженности электрического поля: а) 2D распределение;

б) сечение по оси Х (горизонтальная ось) через фокус; в) сечение по оси Y(вертикальная ось) через фокус

в)

Рассмотрим в качестве еще одного примера дифракцию плоской ТЕ-поляризованной электромагнитной волны длиной волны X = 1 мкм на ди- электрическом цилиндре единичного радиуса с показателем преломления (линза Итона-Липмана) [4]:

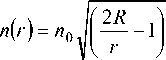
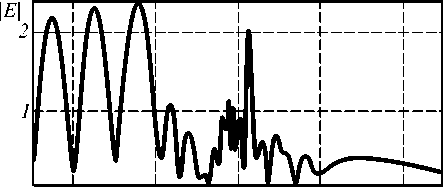
Распределение амплитуды напряженности электрического поля показано на рис. 6.

Здесь n 0 = 2, R = 1 мкм. Общий размер картины дифракции – 5х5 мкм. Количество отсчетов сетки дискретизации – 300х300. Число слоев цилиндра равно 30, а максимальный порядок аппроксимирующих цилиндрических функций – 20.

Из рис. 6 видно, что линза обладает отражающим эффектом, то есть почти весь свет, падающий на линзу, отражается назад. Заметим, что из формулы (11) для показателя преломления линзы Итона-Липмана следует, что при r = 0 показатель преломления стремится к бесконечности. В примере на рис. 6 параметры задачи выбраны таким образом, что в центре линзы при r = 0 показатель преломления равен 14.

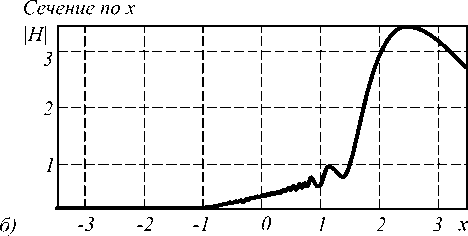
Сечение по у

в)    -3-2-1 О 1   2   3 у

Рис. 5. Распределение амплитуды напряженности магнитного поля: а) 2D распределение;

б) сечение по оси Х через фокус;

в) сечение по оси Y через фокус

Заключение

В работе получены следующие результаты.

Разработан метод анализа дифракции плоской электромагнитной волны с ТЕ- и ТМ-поляриза-циями на неоднородном N-слойном бесконечном диэлектрическом цилиндре, нормальное сечение которого обладает круговой симметрией. Направление падения волны на цилиндр перпендикулярно его образующей.

С помощью данного метода рассчитаны поля дифракции на градиентных диэлектрических линзах с поперечной цилиндрической симметрией, зависимости показателя преломления от радиальной переменной которых выражаются известными формулами: внутренней линзе Лунеберга, обобщенной линзе Лунеберга и линзе-зеркале Итона-Липмана.

На численных примерах показано, что, не смотря на то, что данные градиентные линзы были рассчитаны методом геометрической оптики, они сохраняют свои свойства фокусировки (для линз Лунеберга) и отражения (для линзы Итона-Липмана)

даже при размере радиуса линз сравнимом с длиной волны света, когда лучевое приближение теряет силу. При этом отличие положения рассчитанного максимума интенсивности в области фокуса от заданного геометрического фокуса градиентных линз составило 3-13 %.

а)

Сечение по х

б)-2-101  2 х

Рис. 6. Распределение амплитуды напряженности электрического поля: а) 2D распределение;

б) сечение по оси Х (горизонтальная ось)

Работа выполнена при поддержке гранта Президента РФ № НШ-1007.2003.1 и российско-американской программы «Фундаментальные исследования и высшее образование» («BRHE»).