Дифракционная маска для трехмерного преобразования каустики

Лазеры широко применяются в технологических процессах обработки материалов во многих отраслях промышленности [1]. В последние годы в развитых странах для защиты от фальсификации и неучтенного оборота с успехом начала применяться лазерная защитная маркировка – регистрация информации с помощью эффектов теплового воздействия интенсивного лазерного излучения для получения идентификационных изображений на массовой продукции.

Большое разнообразие продукции и методов маркировки приводят к тому, что для каждой производственной линии необходима специфичная система маркировки. В ряде случаев для маркировки или в целях защиты ценных бумаг от подделок необходимо гравировать конические микроотверстия в толстом слое бумаги или картона. Наиболее распространенными способами лазерной маркировки являются резка путем перемещения остросфокусиро-ванного пучка по контуру изображения и перфорация материала. При перфорации идентификационная метка создается путем воздействия лазерного излучения на всю поверхность материала внутри контура метки одновременно [2]. В таких задачах актуальна лазерная фокусировка излучения в заданную область пространства с заданным распределением интенсивности.

Для лазерной перфорации конических микроотверстий применение обычного фокусирующего объектива является неэффективным, поскольку края отверстия получаются нерезкими. Это связано с тем, что большая часть энергии в каустике объектива концентрируется вблизи оптической оси. Устранить этот недостаток можно перераспределением световой энергии к внешней поверхности каустики таким образом, чтобы на некотором расстоянии от фокальной плоскости энергия фокусировалась в точку (вершина конуса), а в фокальной плоскости – в кольцо.

Задачи расчета оптических элементов и систем для фокусировки лазерного излучения в заданную область пространства с заданным распределением интенсивности в ней рассмотрены в ряде работ [2, 3, 4].

В работах [3, 4] показано, что путем модуляции дифракционной структуры фазовых зонных пластинок можно совмещать функции пропускания линз и фазовых масок. Были оптимизированы пара- метры функции пропускания фазовых масок, преобразующих плоскую волну в кольцо в фокальном пятне. В [2] рассмотрена задача расчета функции пропускания оптического элемента, фокусирующего излучение на поверхность расходящегося конуса. Однако результаты, полученные в [2], не могут быть прямо использованы, если диаметр основания конуса сравним с диаметром кружка Эйри оптической системы.

В [5] предложена лазерная система регистрации оптической информации на фотоноситель с контролем формы записывающего пятна, основным элементом которой, с точки зрения получения равномерного распределения интенсивности в записывающем пятне, является фазопеременная пластинка с линзой, представляющая собой электрооптическую среду с изменяющимся коэффициентом преломления, нанесенная на прозрачную подложку.

Вельдкампом [6] было предложено использовать в системах оптической локации на СО 2 лазере для преобразования лазерного пучка гауссовой моды в пучок с профилем интенсивности, близким к плоскому в дальней волновой зоне, одномерную бинарную решетку. Этот метод обеспечил эффективное формирование пучка с распределением интенсивности, близким к равномерному.

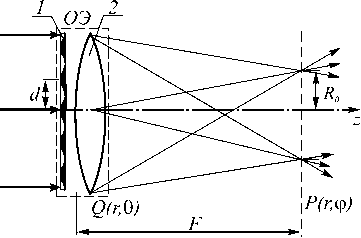
Рис. 1. Схематическое изображение тонкого оптического элемента (ОЭ) и хода лучей через него: 1 - амплитудно-фазовая круговая решетка; 2 - линза

Дифракционные оптические элементы (ОЭ) нашли широкое применение для лазерной обработки материалов. В работе [7] сообщается об экспериментальных результатах гравировки микроотверстий в полимерных материалах и керамике с помощью лазерного пучка с «прямоугольным» распределением энергии в перетяжке. Такое распределение интенсивности в поперечном сечении каустики достигалось путем введения контролируемых (расчет- ных) аберраций в оптическую систему телескопа Галилея с помощью дифракционного ОЭ. При этом длинные растягивающиеся лепестки гауссова пучка были свернуты к центру, что позволило значительно улучшить качество края микроотверстия.

В настоящей работе предложена, рассчитана и экспериментально апробирована дифракционная фазовая маска, позволяющая выполнять 3-х мерное преобразование каустики, а именно – перераспределять световую энергию к внешней поверхности каустики линзы.

где n – целое число, то период решетки 1 связан с диаметром зрачка следующим неравенством:

2 a d > — , n

что при n = 1 дает

d >  2 a .

1. Выбор базовой конструкции объектива

Известно решение задачи расчета функции пропускания оптических систем, фокусирующих в кольцо [2–4]. В работе [8] предложен алгоритм расчета, основанный на интегральном преобразовании Френеля, и определена функция пропускания τ(ρ) тонкого оптического элемента (ОЭ) неограниченной апертуры, фокусирующего плоскую световую волну в кольцо:

т ( Р ) = J 0 ^f Rk Р "I exp f- i-k- P 2 1 .          (1)

I F J \ 2 F J

То есть на зрачке элемента помещается менее одного периода решетки.

В отсутствие маски волновой фронт после ОЭ совпадает с опорной сферой Гаусса линзы 2. У интересующей нас маски R 0 ~ A /2 и фазовая функция

пропускания ОЭ представима как     ( р - R _o ) ², то

2 F

где J o ( ^e ) - функция Бесселя первого рода нулевого порядка; ρ – радиус вектор в плоскости ОЭ, R₀ – радиус кольца в плоскости, находящейся на расстоянии F от плоскости ОЭ, k= 2π/λ – волновой вектор, λ

– длина волны.

Функция (1) состоит из двух сомножителей, один из которых описывает функцию пропускания амплитудно-фазовой маски, второй – функцию пропускания линзы. На рис. 1 показан ход лучей через ОЭ, расположенный в плоскости Q , 1 и 2 – компоненты ОЭ.

есть волновой фронт после ОЭ по-прежнему является поверхностью вращения с той же образующей параболой, что и в отсутствие маски, однако вершина параболы немного смещена с оптической оси. В результате волновой фронт приобретает осесимметричные аберрации и, в первую очередь, сферическую. Поэтому наименьший кружок рассеяния будет наблюдаться в плоскости наилучшей фокусировки, отличной от фокальной.

Наиболее технологичными [3] являются решетки с прямоугольным профилем штриха. Для такого типа решеток в рамках условий (5) и (7) комплексная функция пропускания т _т ( р ) равна:

1, R 1 <  р <  a

■^iv ,0 <  р< R 1 .

Маска 1 является амплитудно-фазовой круговой решеткой с периодом d , который связан с радиусом кольца R₀ следующим соотношением:

^№ d =

R 0

.

Если аксиально-симметричный ОЭ с диаметром зрачка 2 а осветить плоской однородной монохроматической волной, то распределение интенсивности I в фокальной плоскости P , где введены полярные координаты ( r, φ ), имеет вид:

Функция (8) описывает пропускание фазовой маски в виде круговой ступеньки с глубиной по фазе ψ . В работах [3, 9] показано, что наиболее оптимально выбирать ψ = π .

Таким образом, мы показали, что оптическая система ОЭ (см. рис. 2), состоящая из фазовой маски (1) и линзы (2), может сфокусировать излучение в кольцо в фокальной плоскости и одновременно – в точку на некотором расстоянии от нее.

sin

I ( r ) = I о

F (R о—r >

ka ( R о — r )

F

Отсюда следует, что характерная ширина кольца Δ зависит от диаметра зрачка, фокусного расстояния F элемента ОЭ и длины световой волны:

Рис. 2. Базовая оптическая система:

1 – фазовая маска; 2 – фокусирующая линза

A = ^ F

a

.

Если радиус кольца сравним с его шириной

R о ^ nl.

Следовательно, эта оптическая система может использоваться в качестве базовой для решения задачи, поставленной в настоящей работе.

• 2.    Вычислительный эксперимент

  • 2.1.    Расчет распределения интенсивности вблизи фокуса оптической системы

Расчет распределения интенсивности поля в окрестности фокуса (в плоскости Р(r, φ) на рис. 1) тонкого ОЭ выполнен в приближении Френеля:

a

а 2 п a     . kp ²

I ( r , ^z ) = ^fexp i ^7 exp ² о V ^{2 z} J

v

j

г 22 ^ -

V ^ш J

X

, (9)

X T о J 0

,

где exp(- p ²/ ro ²) - радиальное распределение амплитуды гауссова пучка в плоскости входного зрачка; ω - радиус перетяжки; J 0 ( • ) - функция Бесселя пер-

вого рода нулевого порядка.

Функция пропускания оптической системы

имеет вид:

г т о = exp

^^^^^^в

V

. 2

i -Ft ^T m ^(p )

Введем безразмерные переменные:

^P = p ; a = a '; r = r' ; R 1 = R ' . (11) a R 1 a го

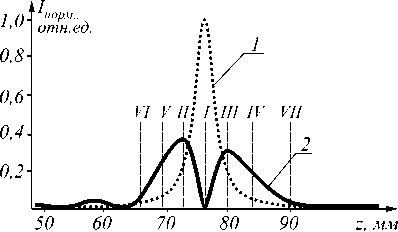
герентном освещении. Расчеты по формуле (12) показали, что критичными для оптимизации являются соотношения между to , R 1 и а . Оптимизация проводилась методом перебора параметров маски до достижения минимума интенсивности дифрагированной волны в фокальной плоскости. Расчеты выполнялись для следующих параметров гауссова пучка и маски: 2 =10,6 мкм; F =75 мм; а =8 мм; ® =3,5 мм. На рис. 3 показано нормированное распределение интенсивности I 0 (0,z) вдоль каустики на оси для одиночной линзы – график пунктирной линией и для линзы с фазовой маской I(0,z) – график сплошной линией. На графике сплошной линией в фокальной плоскости интенсивность падает до нуля, а по обе стороны в пределах глубины фокуса наблюдаются ее максимумы. Такое видоизменение каустики достигается при следующих значениях параметров: R 1 / ® =0,829 и R 1 /a =0,363. Нормировка проводилась на величину максимальной интенсивности на оси в фокальной плоскости для одиночной линзы. Таким образом, зная световой радиус маски а и радиус перетяжки гауссова пучка го , мы всегда можем найти такой радиус ступеньки R 1 , при котором в фокусе будет наблюдаться кольцо. В нашем случае R 1 равен 2,9 мм.

С учетом (11) формула (9) примет вид:

I ⁽ r , z ) =

= —j exp ip'² F - F ))exp - p'²R^,гa^,2) x ^{, (12)}

Я 2 0

^{X T} ( P ') ^J 0 (² P' ^F z r ') P ^d P'

_ 2          _ 2

na        na где Fz =--- и Fy =--числа Френеля.

й г      ^J Xf

Полученное выражение (12) положено в основу вычислительного эксперимента по исследованию формы и характеристик каустики оптической системы «линза+маска» в поперечном и меридиональном направлениях, а также по сравнению этой каустики с каустикой одиночной линзы.

• 2.2.    Распределение интенсивности в поперечных сечениях каустики

В работах [3–4] показано, что при отношении R 1 /a =0,7 в фокальной плоскости будет наблюдаться «кольцеобразное» распределение интенсивности, описываемое разностью функций Бесселя первого рода нулевого порядка в случае однородной монохроматической освещающей волны. Перераспределение энергии достигалось только для плоской волны в одной (фокальной) плоскости. Поскольку в нашей работе актуальна задача перераспределения энергии в объеме каустики в случае гауссова освещающего пучка, то мы исследовали распределение интенсивности вдоль оптической оси (в пределах глубины фокуса) и в поперечных сечениях при ко-

Рис. 3. Графики распределения интенсивности вдоль оси каустики для одиночной линзы – 1 и для линзы с маской - 2. R 1 / ro =0,829 и R 1 /a=0,363

Проведем сравнение распределений интенсивности в следующих плоскостях, обозначенных на рис. 3:

• –    фокальная плоскость – I ;

• –    плоскость фокусировки в точку для системы «линза+маска» перед фокальной плоскостью – II ;

• –    плоскость фокусировки в точку для системы «линза+маска» после фокальной плоскости – III ;

• –    плоскость, в которой интенсивность на оси падает в e ^-2 раз для одиночной линзы перед фокальной плоскостью – IV ;

• –    плоскость, в которой интенсивность падает в e ^-2 раз для одиночной линзы после фокальной плоскости – V ;

• –    плоскость, в которой интенсивность падает в e ^-2 раз для системы «линза+маска» перед фокальной плоскостью – VI ;

• –    плоскость, в которой интенсивность падает в e ^-2 раз для системы «линза+маска» после фокальной плоскости – VII .

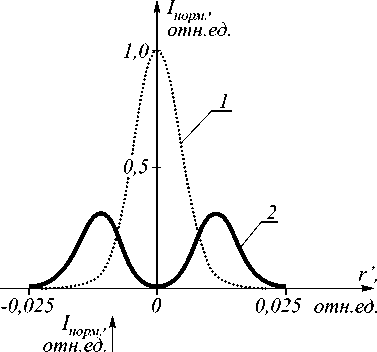
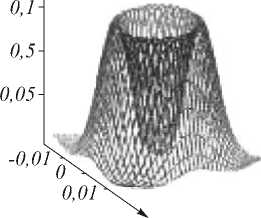
Проведем анализ распределения интенсивности I в фокальной плоскости при z = F. На рис. 4а представлен график зависимости распределения интенсивности от r′ для одиночной линзы (график 1) и для системы «линза+маска» (график 2) в плоскости z = F. На рис. 4б изображен трехмерный график этого распределения для системы «линза+маска», который наглядно иллюстрирует перераспределение энергии в кольцо в фокальной плоскости.

г’, отн.ед.

Рис. 4. а) графики распределения интенсивности в фокальной плоскости: 1 – для линзы и 2 – для линзы с фильтром; б) объемный график распределения интенсивности I(x,y) в фокальной плоскости для линзы с маской

Обычно представляют интерес следующие характеристики фокального кружка: D – диаметр кольца по уровню e^-2; Δ – ширина кольца по уровню e^-2; D₁ – диаметр кольца ( D₁ = 2 R₀ ); I_max,k – значение максимальной интенсивности в кольце; I_max,kr – значение максимальной интенсивности в кружке Эйри; Δ Эйри – диаметр кружка Эйри по уровню e^-2 (рис. 5). В таблицу 1 сведены расчетные значения этих характеристик.

Таблица 1.

D, мкм	Δ, мкм	I max,k , %	I max,kr , %	Δ Эйри , мкм	D 1 , мкм
304	116	15	100	150	182

Из таблицы 1 видно, что диаметр фокального пятна D для системы «линза+маска» увеличивается приблизительно в 2 раза по сравнению с диаметром ΔЭйри кружка Эйри. Ширина кольца Δ сравнима с диаметром кружка Эйри. Величина интенсивности в максимуме кольца Imax,k ≈ Imax,kr/6, что связано с перераспределением энергии падающего излучения по большей площади.

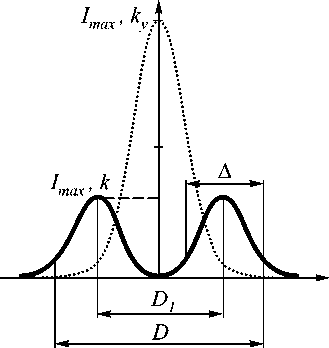
Рис. 5. Обозначение характеристик фокального кружка

Теперь исследуем распределение интенсивности в плоскостях I , III , IV , V , VI и VII . В таблице 2 приведены расчетные значения z –координаты, интенсивности I max (z) , ширины светового пятна Δ i и D i в выбранных плоскостях для одиночной линзы и для системы «линза+маска», соответственно.

Из таблицы 2 видно, что во всех характерных плоскостях вдоль каустики размеры пятен D i для системы «линза+маска» меньше, чем ширина светового пятна Δ_i в этих плоскостях для одиночной линзы.

Таблица 2.

Выбранная плоскость		Одиночная линза		Система «линза+ маска»
Обозначение	Координата z , мм	I max , %	Δ i , мкм	I max , %	D i , мкм
II	71,7	19	338	36	186
III	78,55	16	350	30	198
IV	71	13	395	34	187
V	79	12,8	404	29	206
VI	65,6	2,7	875	4,9	494
VII	86,75	1,7	978	4	600

Максимальная интенсивность на оси в центре пятна в выбранных плоскостях вдоль оси z системы «линза+маска» приблизительно в два раза больше интенсивности в соответствующей плоскости для одиночной линзы. Это говорит о том, что в этих плоскостях энергия в каустике системы «лин-за+маска» распределена по меньшей площади, чем у одиночной линзы. Сравнивая плоскости II и III, можно сделать вывод, что распределение интенсивности в пределах глубины фокуса системы «лин- за+маска» несимметрично относительно фокальной плоскости: в плоскости II максимальная интенсивность в пятне на оптической оси больше, чем в плоскости III. К тому же спад интенсивности после плоскости III более пологий. Диаметры пятен в этих плоскостях приближаются к диаметру кружка Эйри для одиночной линзы в фокальной плоскости (см. таблицу 1).

На рис. 6 представлены программно– синтезированные изображения световых пятен для одиночной линзы (а) и для системы «линза+ маска» (б) в сечениях каустики между фокальной плоскостью I и плоскостью фокусировки в точку II, а рис. 6б наглядно иллюстрирует влияние фазовой маски на структуру поля.

Плоскость I

Рис. 6. Програмно-синтезированные изображения световых пятен (а) в сечениях каустики для одиночной линзы; (б) для системы «линза+маска»

• 2.3.    Распределение интенсивности в меридиональном сечении каустики

Более полное представление о распределении энергии в каустике можно получить, если дополнительно построить изофоты в ее меридиональном сечении. Рассмотрение меридионального сечения позволяет сравнить глубину фокуса A z л+м системы «линза+маска» с глубиной фокуса одиночной линзы A z л . Именно глубиной фокуса будут определяться параметры конических микроотверстий, такие как высота конуса, угол конуса, диаметр основания.

В [10] выполнено классическое рассмотрение этой задачи для хорошо коррегированной линзы, построены изофоты для случая плоской освещающей волны.

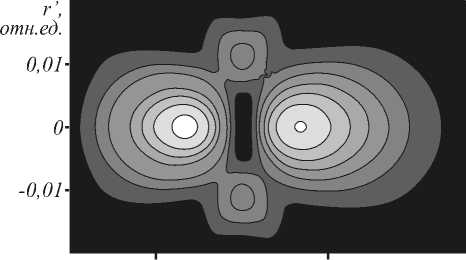
В настоящей работе распределения интенсивности для одиночной линзы и для системы «лин-за+маска» для случая гауссовой освещающей волны вычислены посредством MathCAD 2000/Pro. На рис. 7 показаны изофоты вдоль каустики в меридиональ- ном сечении. Области равной интенсивности имеют одинаковую яркость. По горизонтальной оси откладывается z - координата, а по вертикальной - г'ко-ордината. Сравнивая изофоты линзы и системы «линза+маска», можно сделать вывод, что глубина фокуса системы превышает глубину фокуса одиночной линзы.

70               80 z, лш

70               80 z, мм

Рис. 7. Изофоты в меридианальной плоскости вблизи фокуса для гауссовой волны: а) для одиночной линзы;

б) для системы «линза+маска»

Обычно глубину фокуса A z для фокусирующих систем определяют как расстояние от фокальной плоскости до плоскости, в которой происходит спад интенсивности на 20 %. Найдем A z из формулы (13) для одиночной линзы ( Т 0 = 1) при плоской освещающей волне. Распределение интенсивности для точек, лежащих на оси, описывается следующим выражением:

• ²       F — F_f )

I л , норм (0, z ) = A™ c ² 1          I .         (13)

z V 2    )

В формуле (13) нормировка проведена на максимальную интенсивность в фокусе на оси. Приравнивая I_л,норм( 0 , z) к 0,8 и полагая, что вблизи фокуса f / z ® 1 , получим выражение для оценки A z_л :

л + 1 ^ 2 ^{A z} л =±?” 2 a

.

Теперь оценим глубину фокуса системы «лин-за+маска» - A z_л+м . Для этого так же вычислим интеграл (12) для т ₀ = т _т и г ' = 0, интенсивность запишется как:

(

I (0, z ) =

2 F z

-

V

F z

^^^^^^»

F f )

x

M 1  1     1

^т зп ⁽p ) = т—; L -exp

^{2 n} p =-» P

^  2p , p 0           _

x cosl

F z

F f

a'

-

1 - cos l

F z

F f

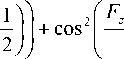
F f

= . (15)

где p – нечетное целое. Каждое слагаемое ряда (18) описывает функцию пропускания линзы с

= 0,8

Уравнение (15) – трансцендентное, и в явном виде выразить A z не удается. Задавая необходимые параметры, можно рассчитать A z для конкретного случая.

Была проведена оценка глубины фокуса A z с помощью встроенных функций MathCAD 2000/Prо. Расчеты показали, что значение глубины фокуса для A z л , оцененное по спаду интенсивности на 20%, составило 0,8 мм, а для системы «линза+маска» A z л+м – 3,45 мм.

Таким образом, в ходе численного моделирования была получена наглядная модель каустики системы «линза+маска», изучены ее свойства и проведено сравнение с каустикой обычной фокусирующей линзы. Показано, при совмещении маски и линзы происходит трехмерное видоизменение каустики. В фокальной плоскости энергия фокусируется в кольцо, диаметр которого в два раза больше диаметра кружка Эйри для одиночной линзы. При этом критичными являются как параметры маски ( а и R₀ ), так и радиус перетяжки гауссова пучка ω . При увеличении ω отношение R 1 /а =0,363 приближается к отношению R 1 /а =0,7, полученного для плоской волны. На некотором расстоянии от фокальной плоскости энергия фокусируется в точку, диаметр которой сравним с диаметром кружка Эйри в фокальной плоскости. При этом происходит удлинение глубины фокуса «линза+маска» приблизительно в четыре раза по сравнению с глубиной фокуса одиночной линзы.

фокусом F = ^p 0-. Зонная пластинка действует A p

подобно системе, состоящей из набора положительных и отрицательных линз с совмещенными главными плоскостями.

Рабочим порядком в эксперименте является +1, в области каустики которого остальные порядки дают паразитную засветку малой интенсивности, не влияющую на изучаемую картину. Поэтому в окрестности фокуса +1 порядка в сумме (18) можно пренебречь всеми слагаемыми, кроме p =1:

^Т зп ⁽p ) = —exp m

ik p p 2 F 1

3. Экспериментальные исследования

и действие ЗП на освещающий пучок эквивалентно действию одной линзы.

Важным свойством зонных пластинок является возможность видоизменять каустику путем изменения топологии зон [11]. В нашем случае трансформирование зон проведено следующим способом: в центральной части зонной пластинки непрозрачными являются нечетные зоны, а на периферии – четные. А именно, порядок чередования прозрачных и непрозрачных зон меняется по достижении радиуса R_{1 .} Тем самым вносится дополнительный сдвиг фаз п между проходящими волнами. По сути, это эквивалентно внесению фазовой маски, имеющей сбой на радиусе R 1 . Таким образом, в структуре модулированной зонной пластинки закодирована функция пропускания оптической системы, состоящей из одиночной (положительной) линзы и фазовой маски.

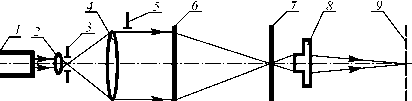
На рис. 8 представлена принципиальная оптическая схема экспериментальной установки.

Для проведения эксперимента использовалась амплитудная зонная пластинка (ЗП) Сорэ (центр – темный), состоящая из последовательно чередующихся прозрачных и непрозрачных концентрических колец, радиусы которых удовлетворяют следующему соотношению:

Т

P m

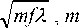
целое,

где p m - радиус m - ой зоны Френеля; m - номер зоны Френеля; f – фокусное расстояние для пучков, дифрагировавших в +1 порядок.

Функция пропускания ЗП Сорэ [11] имеет вид:

1 (2m + 1)Af < pm < (2m + 2)Af

Тзп (p) = I 0,     2mAf < pm, < (2m + 1^Af ,(17)

m = 0,1,2...

Функция пропускания (17) может быть представлена [11] в виде:

Рис. 8. Принципиальная оптическая схема экспериментальной установки

Световой луч от He-Ne лазера 1 ( λ =0,63 мкм) расширяется микрообъективом 2 (40^х). Объектив (5) ( F =300 мм) формирует параллельный пучок, который дифрагирует на зонной пластинке (6). Ирисовая диафрагма 5 в выходном зрачке объектива (4) изменяет рабочую апертуру пучка. Изображение сечения каустики в плоскости (7) строится на экране (9) микрообъективом (8), который перемещается в пределах всего фокального отрезка. Апертура объектива (8 ^х ; 0,2) (8) значительно превышает выходную апертуру (~0,065) исследуемых ЗП и микроскоп не вносит собственных аберраций. Изображение на-

блюдается визуально либо регистрируется цифровым фотоаппаратом CASIO QV-3500EX.

Целью эксперимента являлось изучение каустики модулированной ЗП Сорэ.

На рис. 9 приведены фотографии сечений каустики модулированной ЗП с фокусным расстоянием f зп =158 мм, световым радиусом а =10,078 мм и радиусом сбоя R 1 =6 мм. На рис. 9а представлено изображение сечения каустики в фокальной плоскости. При этом соотношение между радиусом сбоя и световым радиусом ЗП не соответствует оптимальному.

а)

б)

Рис. 9. Изображения сечения каустики в фокальной плоскости:

а) с открытой диафрагмой (R1/a=0.13; z = 158 мм); б) с закрытой диафрагмой (R1/a=0,7; z = 75 мм)

Если уменьшить диафрагму таким образом, чтобы отношение R 1 /a стало оптимальным, то энергия в фокусе перераспределится в кольцо (рис. 9б) к внешней поверхности каустики.

На рис. 10 приведены экспериментальные фотографии световых пятен в сечениях каустики модулированной ЗП Сорэ от фокальной плоскости I до плоскости фокусировки в точку II. Фотографии на рис. 10 соответствуют изображениям на рис. 6 между плоскостями I и II. В эксперименте нам удалось получить перераспределение энергии в каустике, согласующееся с расчетным. На рис. 10 ясно видны интерференционные кольцевые полосы от паразитного 0-го порядка дифракции.

Плоскость II

Рис. 10. Фотографии световых пятен в сечениях каустики, модулированной ЗП Сорэ

Горизонтальным микроскопом проведены измерения следующих характеристик каустики (см. рис. 6): 1) диаметра кольца – D ; 2) ширины кольца – Δ; 3) диаметра пятна в плоскости II фокусировки в точку – D ′ ; 4) глубины фокуса – Δ z . Полученные результаты измерений сведены в таблицу 3.

Видно, что экспериментальные и расчетные данные близки.

Таблица 3.

Параметр	Расчетные данные	Эксперим. данные
D , мкм	42	56
Δ, мкм	15	10
D ′ , мкм	20	17
Δ z , мкм	1000	1000

Выводы

В работе показано, что фазовая маска в виде круговой ступеньки глубиной π рад по фазе позволяет перераспределить энергию к внешней поверхности конуса в каустике. В фокальной плоскости I происходит фокусировка гауссова пучка в кольцо. По мере удаления от плоскости I вдоль оси z интенсивность в центре кольца увеличивается до тех пор, пока произойдет фокусировка излучения в световое пятно – в плоскости I или II . При этом найдены критичные параметры оптимизации – радиус сбоя в маске, световой радиус маски и радиус перетяжки гауссова пучка. Проведена оптимизация оптической системы и найдены соотношения между этими параметрами: R 1 / ω =0,829 и R 1 /а =0,363.

В ходе численного моделирования построены графики распределения интенсивности вблизи фокуса для одиночной линзы и для системы «лин-за+маска», проведено изучение и сравнение каустик данных оптических систем. Расчеты показали, что ширина кольца Δ соизмерима с диаметром кружка Эйри ∆ _Эири = 1,22 ∆ , причем диаметр пятна в плоскости фокусировки в точку для системы «лин-за+маска» также приблизительно равен этому параметру. Программно синтезированы изображения световых пятен вдоль оси z , а также вычислены изофоты в меридианальном сечении каустики. Показано, что глубина фокуса системы «линза+маска» в четыре раза больше глубины фокуса одиночной линзы, оцененной по спаду интенсивности на 20%.

В ходе экспериментальной части проведены модельные эксперименты с модулированными зонными пластинками, в структуре которых закодирована функция пропускания расчетной оптической системы, состоящей из хорошо корригированного объектива и фазовой маски. Экспериментальные данные согласуются с расчетными и подтверждают возможность перераспределения энергии в каустике.

Применение фазовых масок для трехмерного преобразования каустики в системах лазерной маркировки путем перфорации высококачественных конических отверстий в материале позволит улучшить их скоростные и точностные характеристики, обеспечивая высокую степень защиты от копирования другими способами.