Дифракционные характеристики линзы Люнеберга для поля круговой поляризации

Антенные системы, построенные на базе линзы Люнеберга (ЛЛ), являются сравнительно новым типом направленных антенн. Основным преимуществом таких антенн становится возможность широкоугольного сканирования при фиксированном положении основного элемента конструкции тела линзы. Сканирование лучей осуществляется путем перемещения слабонаправленных облучателей по внешней поверхности линзы. Антенны на базе ЛЛ используются для военных целей и космической связи [1]. Чтобы линза фокусировала слабонаправленное излучение облучателя, коэффициент рефракции материала линзы должен удовлетворять следующему закону [2]:

n ( r ) = 7s'( r ) = ^2 - ( r / a )² = V2 - r ², (1) где ε′ – относительная диэлектрическая проницаемость материала линзы в точке r ; r – радиальная координата в сферической системе координат; a – внешний радиус линзы.

Технически линза реализуется в виде концентрических сферических слоев, для которых диэлектрическая проницаемость удовлетворяет условиям закона (1). На ряду с основным облучателем могут использоваться дополнительные источники излучения, удаленные от поверхности сферы, которые формируют диаграммы, используемые, например, для подавления организованной помехи или отражения от местных предметов на местности. В связи с этим представляет интерес дифракционная задача для ЛЛ.

В работе исследуются дифракционные характеристики ЛЛ при облучении электромагнитными волнами круговой поляризации. На ряду с диаграммами рассеяния и коэффициентами дифракции определяется коэффициент эффективности по основной поляризации (« оп »). Появление кросс-поляризации (« кп ») обусловлено наличием границ разделов слоев и кривизной поверхностей линзы.

1. Диаграммы рассеяния линзы при дифракции

Дифракционные характеристики ЛЛ для линейной поляризации поля исследовались ранее [3]. Поле источника, удаленного на бесконечность, формирует поле круговой поляризации. Задача решается в сферической системе координат, волна внешнего источника падает с направления θ=0, ϕ=0. Сторонний ток, который формирует падающее поле, имеет следующий вид:

I _оп = ₂ ( α a _θ ± 1

- a² exp ( j v ) а _ф

где 0 ≤α≤1; ψ – разность фаз между двумя ортогональными составляющими тока; йд, й^ — единичные векторы в сферической системе ко- ординат.

При α=1/ 2 и ψ = ±π /2 формируется поле круговой поляризации правого и левого вращения.

а )

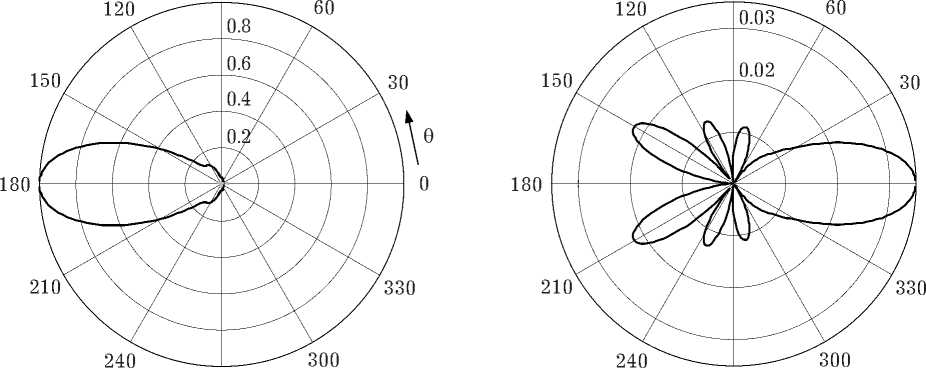
б )

Рис. 1. Диаграммы рассеяния для «« оп » ( а ); фрагмент в увеличенном масштабе диаграммы рассеяния для « кп »( б )

Задача электромагнитного возбуждения удаленным источником решается с использованием тензорных функций Грина и методик, изложенных в [4]. Вектор напряженности электрического поля дифрагированной волны в случае поля круговой поляризации в дальней зоне определяется следующим образом:

^-         exp ( -ik o r )^ 2 n + 1     Г.п )

E ( 9 ) = E о------------- 7 ---------ехр I i n I х

( к о r )     П = 1 n(n + 1 )    v 2 J

х

—

ехр ( i ф ) ([ a 9 ^T n (9) + ia ^ n n (9)] M n — [ a _e n n (9) + ШфТ n (9)] N n) ,

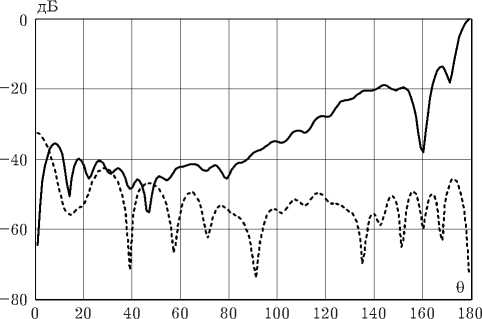
Рис. 2. Диаграммы рассеяния линзы по « on » и « кп » для к о a = 8 п

где к о = 2п / X — волновое число;

cP n (cos_9)            P^jcosG)

^т n ^{( 9 )}                     , ^п n ^{( 9)}         . _А ;

d9                  sin 9

P n (cos 9) - функция Лежандра;

М'

n

—‘ iZn (a) jn (ко a) — Jn к a)

,

— _'

iZ n ( a ) h n ( к о a ) — h n ( к о a )

—w —

'

N'

n

^iYn ⁽ a ) j n ^{( k} 0 a ) ^— j n ^{( k} 0 a )   [4]_;

iY — n ( a ) h n (к о a ) — h n ( к о a )

h _n ( x ), j _n ( x ) – сферические функции Бесселя – Рикатти [5]; Z _n , Y _n ( a ) — ориентированные направленные импедансы и адмитансы, которые определяются последовательным пересчетом от внешней границы ЛЛ к центру через частичные области-слои по методике [4].

Поля « оп » и « кп » определяются стандартным способом как скалярное произведение двух векторов. Поле основной поляризации определяется как

1 ^-,-     - X

E on = л/2 E ⁽ a 9 + ja Ф ^).

Поле кросс поляризационной составляющей определяется как:

1   ^-,-

^Е кп = ^у2 E ^{( a} 9 ^ja ф )■                             ⁽⁵⁾

Для определенности в качестве « оп » выбрано поле правого вращения. Численные расчеты полей и дифракционных коэффициентов выполнены для шестислойной модели линзы. Относительная диэлектрическая проницаемость отдельных слоев выбирается для средней точки слоя в соответствии с формулой (1) при равношаговой аппроксимации ширины слоев. Диэлектрическая проницаемость материала слоев выбирается комплексной, что позволяет в дальнейшем учесть омические потери в линзе.

В качестве примера на рис. 1 в полярной системе координат приведены рассеянные поля « оп » и « кп » для к о a = 2п ( 2 a = 2X ) . Поля на рис. 1, а и б имеют общую нормировку.

С увеличением радиуса линзы концентрация энергии в направлении 9 = 189° увеличивается.

На рис. 2 в декартовой системе координат в логарифмическом масштабе представлены диаграммы рассеяния по « оп » и « кп » для увеличенного радиуса линзы к о a = 8п. Сплошной линией показан уровень по основной поляризации, пунктирной – по кросс-поляризационной составляющей.

Для других диаметров линзы основные вторичные характеристики диаграммы направленности приведены ниже в табл. 1.

2. Дифракционные коэффициенты

Концентрированный эффект рассеяния электромагнитной волны при дифракции и доля

омических потерь описываются квадратичными дифракционными коэффициентами. Перечислим основные дифракционные коэффициенты:

1) о _s — коэффициент рассеяния, определяется

о(6, ф; 6 i, ф i) = lim r ^да

2 r V |n s , кп ⁽⁶, ^ф)| a ^J |П i ( 6 i , Ф i )|

отдельно для « оп » и « кп »:

^о s , оп

Р оп п a ² |fi i|

^о s , кп

р кп п a 2 |Й i|

где ri s , оп ( ⁶, ф)| , |й s , кп ( ⁶, ф)| ^- модуль вектора Пойнтинга рассеянной волны для угла 6.

Запишем двухпозиционные коэффициенты рассеяния для случая круговой поляризации:

где п a ² — площадь проекции препятствия на

фронт набегающей волны; P _оп , P _кп – мощность,

рассеянная полем « оп »- и « кп »-составляющих соответственно; |Й i | = | ^ о 2 / (2 Z q ) — абсолютное значение действительной части вектора Пойн-тинга падающей волны.

Методика получения расчетных формул для линейной поляризации падающего поля изложена в [4]. Аналогично получены формулы для случая круговой поляризации. Запишем общие коэффициенты рассеяния для « оп »- и « кп »-составляющих поля:

л ”

оs,оп(6) = —^ У (2n + 1) (|Mn|2 + Nn2),(7)

(k0 a) n=1           V7

^, оs,кп(6) = —2 У (2n + 1) ( Mn2 - Nn2).(8)

(k0 a) n=1           V7

_ х 4 о(6,6) =-----.

ⁱ ( k 0 a )²

У^(2 п + 1) (-1) n _х , n ( n + 1)

n = 1

х( [ т n (6) -п n (6) ] . [ M n

„ '    4

о(6,6) =-----.

ⁱ ( k 0 a )²

⁺ N n ^]) ,

j^(2 n + l) (-1) n х ^—* n ( n + 1)

n = 1

х( [ т n (6) + п n (6) ] . [ M n

^- N n ]}

3) частными случаями двухпозиционных коэффициентов рассеяния являются радиолокационный о(0, 0) и попутный о(п, 0) коэффициенты рассеяния:

^о кп , рад ^{( 6}, ^ф; ⁰ , ⁰⁾

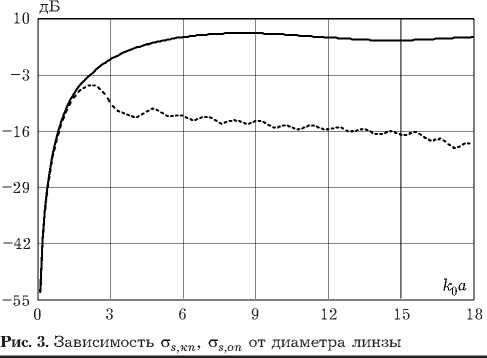
При выводе формул (7) и (8) использовалась ортогональность полиномов Лежандра и их производных. На рис. 3 приведены графики зависимости о _{s кп} (показано пунктирной линией) и о _{s оп} (показано сплошной линией) от размеров линзы k ₀ a ;

2) о ( 6, 6 i ) — двухпозиционные коэффициенты рассеяния для « оп »- и « кп »-составляющих, которые характеризуют интенсивность рассеяния в определенных направлениях.

2 ( k 0 a )²

да

У (2 n + 1)[ Mn n=1

^о оп , попут

(6, ф ;0,0)

о

(6, ф; 6 i, ф i) = lim r ^да

2 r ^ 2 | Й s , оп ( ⁶, ф)| a J |fi i ( 6 i , Ф i )|

^- N n ^]

2 ( k 0 a )²

да

У (2n + 1)[Mn n=1

+ N n ]

Радиолокационный коэффициент рассеяния (в направлении падающей волы, 6 = 0, ф = 0) равен нулю для « оп »-составляющей и имеет максимальной значение для « кп ». Для попутного коэффициента рассеяния (при 6 = п, ф = 0) максимум излучения определяется только полем « оп ».

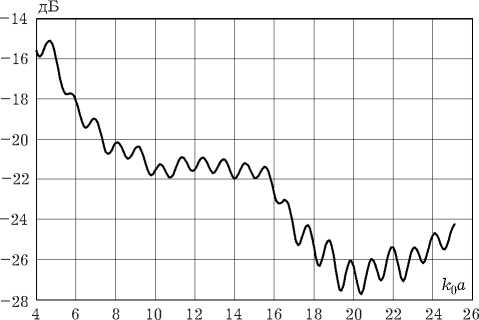
Рис. 4. Потери энергии на образование поляризационных потерь при круговой поляризации

линзы k o a = 8п. Как видно из таблицы, основное влияние на уровень потерь в материале линзы, оказывает на ст a .

3. Поляризационные потери

Потери на переизлучение, связанное с полем паразитной поляризации в некотором конусе углов 9 о или во всем полупространстве, могут характеризоваться коэффициентом потерь а, который определяется как отношение мощности, излученной полем « кп » к суммарной мощности, переизлученной рассеивателем:

Ниже в табл. 2 приведены расчетные данные по радиолокационному и попутному коэффициентам рассеяния для трех радиусов линзы;

4) ст a — коэффициент поглощения, определяется с использованием оптической теоремы [6]:

ст s, кп а =-------,------- ст s, кп + ст s, оп

^ст а

Pa пa2 |пJ

где P _a – полная поглощенная препятствием

мощность.

Коэффициент поглощения описывается следующей формулой [4]:

ст а ( а ) =

2 ( k 0 a )²

f (2 n + 1)

n = 1

X

x Re

____________ iZ ( a ) __________

I iZ ( a ) h <2) ( k o a ) - b n² ( k o a )|

|iY ( a)hn\k o a ) - hn^a ) 2

Ниже в табл. 3 показано влияние омических потерь материала линзы (Im s') на определенные выше коэффициенты рассеяния при радиусе

Поляризационная эффективность по « оп » линзы ц при этом определяется через коэффициент поляризационных потерь ц = 1 - а, на рис. 4 приведена зависимость изменения коэффициента поляризационных потерь а от радиуса линзы k o a .

Колебательный характер коэффициента а при больших значениях радиуса линзы обусловлен наличием большого количества боковых лепестков, что является следствием интерференции волн, переизлученных отдельными участками объемной структуры неоднородной линзы.

Заключение

Показано, что многослойная линза Люнеберга при облучении падающей волной круговой поляризации может быть использована для эффективного формирования луча в попутном направлении с теневой стороны линзы. Дифракционный режим работы линзы может быть использован параллельно с антенным режимом. Дополнительные лучи могут быть использованы для подавления организованных помех или отражения от местных предметов.

Таблица 1

Вторичные характеристики линзы для различных диаметров

k 0 a	2А0 по 3 дБ	V 1 , дБ	E max кп , дБ
2п	36°	–18	–28
4п	14°	–12	–30
8п	6°	–14	–32

Примечание:

2А0 — ширина диаграммы направленности;

V 1 — уровень первого бокового лепестка, дБ;

E _{max кп} – максимальный уровень « кп »-составляющей.

Таблица 2

Попутный и радиолокационный коэффициенты линзы

k 0 a	2π	4π	8π
σ попут , оп (θ), раз (дБ)	94,74 (19,8)	246,17 (23,9)	971,65 (29,9)
σ радиолокац , кп (θ), раз (дБ)	0,225 (–6,5)	0,15 (–8,3)	0,118 (–9,3)

Таблица 3

Влияние омических потерь на коэффициенты рассеяния

-Im ε′ σ	0	0,01	0,1
σ s , оп , раз (дБ)	3,5 (5,5)	3 (4,7)	1,73 (2,38)
σ s , кп , раз (дБ)	0,013 (–18,8)	0,011 (–19,4)	–0,004 (–24,3)
σ a , раз (дБ)	0	0,128 (–8,9)	0,46 (–3,4)
σ попут , оп , раз (дБ)	971,6 (29,9)	967,7 (29,8)	941,3 (29,7)
σ радиолокац , кп , раз (дБ)	0,118 (–9,3)	0,111(–9,5)	0,087 (–10,6)

Luneberg lens dissipation properties for electromagnetic field of circular polarization

B.A. Panchenko, D.V. Denisov