Дифракционные объективы на параболических поверхностях

ДИФРАКЦИОННЫЕ ОБЪЕКТИВЫ НА ПАРАБОЛИЧЕСКИХ ПОВЕРХНОСТЯХ

По-видимому, впервые С.М. Райский [1] в начале 50-х годов и Габор в середине 60-х [2] предложили выполнять дифракционный объектив (ДО) на поверхностях вращения, образующая которого описывается кривой второго порядка. С.М. Райский указывал, что из-за разного знака кривизны фронтов для источника, помещенного на расстоянии А от плоской зонной пластины и наблюдателя в точке В, удлинение оптического пути на величину, равную А/2, достигается весьма малым увеличением угла а (угол между оптической осью и направлением на n-ю эону Френеля). Поэтому для плоской зонной пластины разность хода, выраженная в А/2 (число зон Френеля), принимает весьма большие значения при сравнительно малых углах а [1].

Для получения светосильной дифракционной оптики, имеющей широкие зоны Френеля при большом отверстии и малом фокусном расстоянии, в [1] предложено использовать сферическую поверхность, которая позволяет обеспечить одинаковый знак кривизны волновых фронтов А и В. Указано [1], что для "сферического” дифракционного объектива устраняется сферическая аберрация.

Позднее Габор отмечал [2], что ДО можно сконструировать так, чтобы он соответствовал части сферы с центром в ее фокальной точке. По замыслу в таком ДО существенно уменьшаются аберрации типа комы и появится возможность выполнять сканирование пучка с весьма большими углами при помощи смещения источника излучения [2] .

Теоретическому (аналитическому) изучению элементарных сравнительных фокусирующих свойств радиообъективов СВЧ диапазона, выполненных на плоской и сферической поверхностях, посвящена работа [3].

В ней было получено трансцендентное уравнение для определения радиусов зон

Френеля на поверхности объектива. Рассматривая случай, когда длина волны X много меньше ширины крайней зоны Френеля, что может иметь место в СВЧ диапазоне, радиусы зон Френеля можно определить из более простого приближенного уравнения [з].

(А+В)² „. , Ja+B C^ar^{a n} I г

+ (A^B.2J2 _

С2

(A-В)(А+В)² гС²

2 (— + 1) Г

R2 + С2

2(А2+В2) +

где С = А+В+пЛ/2; г - радиус сферы ДО.

Используя приближение геометрической оптики, авторами цитируемой работы приведен анализ влияния точности установки источника излучения в фокусе на величину перемещения области фокусировки вдоль оптической оси. Так, если "а” -новое расстояние источника излучения до ДО, то новое фокусное расстояние "Ь” определяется выражением [з]:

[ {а+[г-Лг2^2) ]} 2 + R2]1/a + [{b-[r-Vr2-R2]}2 + R2] ^a - (a+b+X/2) = 0.

Анализ этого выражения показал, что в случае A»D изменение его положения не способно вносить изменение в фокусное расстояние.

Численные расчеты, проведенные при следующих значениях: aQ=60 см, bQ*10 см, D=80 см, Ло=3,2 см, показали, что у ДО со сферической поверхностью полуширина распределения интенсивности поля вдоль оптической оси несколько уже, чем у зонной пластины. В то же время уровень боковых лепестков в изображении точки мень ше, чем у аналогичной зонной пластины, при этом значение интенсивности поля в области фокуса "сферического" ДО определялось по выражениям [3]:

N

А = М f (-1(«ар+Га1>)]'

an= S^n + (a0+xn)2+...+Vk2-(b-xn)2},

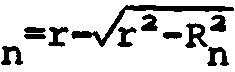
В более поздних работах этих авторов проведено исследование ДО на параболической поверхности [4] и сравнение фокусирующих свойств "параболических", "сферических" и "плоских" ДО [5] в сантиметровом диапазоне длин волн. В первой из указанных работ приведены выражения для радиусов зон Френеля для соответствующего типа ДО и показано, что наиболее узкую полуширину распределения интенсивности поля в области фокуса вдоль оптической оси обеспечивает "параболический" радиообъектив. Это свойство авторами указанных работ объясняется тем, что для "параболического" ДО число зон Френеля, укладывающихся на его апертуру превосходит это значение в случае "сферического" и "плоского" ДО.

В работе [4] исследования проведены для "параболического" ДО. Численно были определены частотные свойства такого ДО в диапазоне от 8075 МГц до 10875 МГц.

В указанной работе приведена система уравнений для вычисления радиусов зон Френеля на параболическом ДО, когда на выпуклую сторону радиообъектива п ад ает сферический волновой фронт.

Было показано, что для ДО с Л =3,2 см (fQ=9375 МГц), ао=50 см, Ь =24 см и N=12 фокусное расстояние в указанном диапазоне частот изменялось от 16 см до 34 см.

В то же время известные работы по изучению фокусирующих и частотных свойств таких объективов не позволяют достоверно судить об их характеристиках, так как соответствующие экспериментальные исследования отсутствуют. Кроме того, не выяснен вопрос о фокусировке излучения от внеосевого источника. В настоящей работе приведены результаты экспериментальных исследований фокусирующих и частотных свойств параболических (одно- и двухкомпонентных) дифракционных объективов СбЗ.

Расчет дискретной фазовой функции объектива (зон Френеля), преобразующего расходящийся сферический волновой фронт в сходящийся сферический, осуществлялся по выражениям, приведенным в [4]:

v^+U+b^T3 + V^V^H? - a+b0 + ^

VRn/4F

Рассмотрим разрешение параболического объектива. Вид дифракционного пятна, сформированного таким объективом, приведен на рис. 1 для различных значений частот излучения. Сплошной кривой показан вид дифракционного пятна для зонной пластины [7]. Анализ приведенных на рис. 1 данных показывает:

• 1.    Параболические радиообъективы, так же как и плоские [7] , обеспечивают разрешение, близкое к дифракционному пределу, в широкой области спектра (+20,65%, -16,3%).

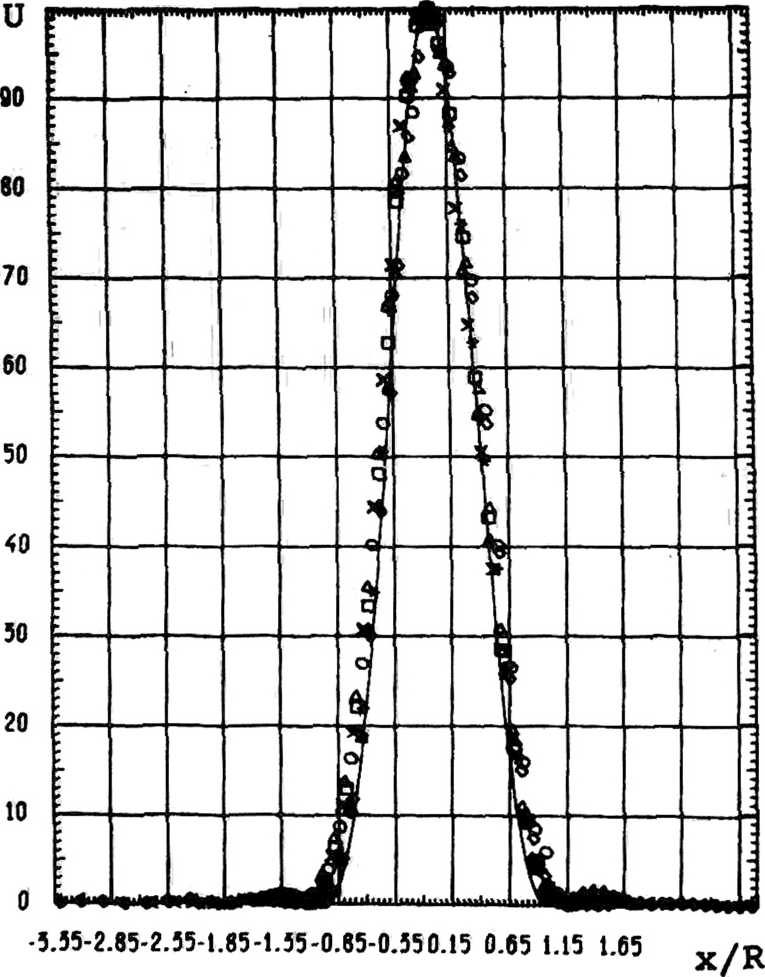
Рис. 1. Дифракционное пятно для параболического объектива:

ДХА0,%

ХХХ+20.65 □ □□+14.35 ООО +8.69 ДАД -5.41 000-13.04 ЖЖ Ж-16.30

• 2,    Для параболических радиообъективов уровень боковых лепестков в распределении интенсивности поля в области фокуса меньше аналогичной величины для плоского радиообъектива в среднем на 20-40%.

Распределение интенсивности поля вдоль оптической оси для различных волн источника излучения, отличных от расчетной Хо, приведено на рис, 2. Приведенные экспериментальные результаты показывают, что ширина распределения интенсивности поля вдоль оптической оси, определенная по первым нулям, в среднем на 15-20% меньше аналогичной характеристики плоского дифракционного объектива.

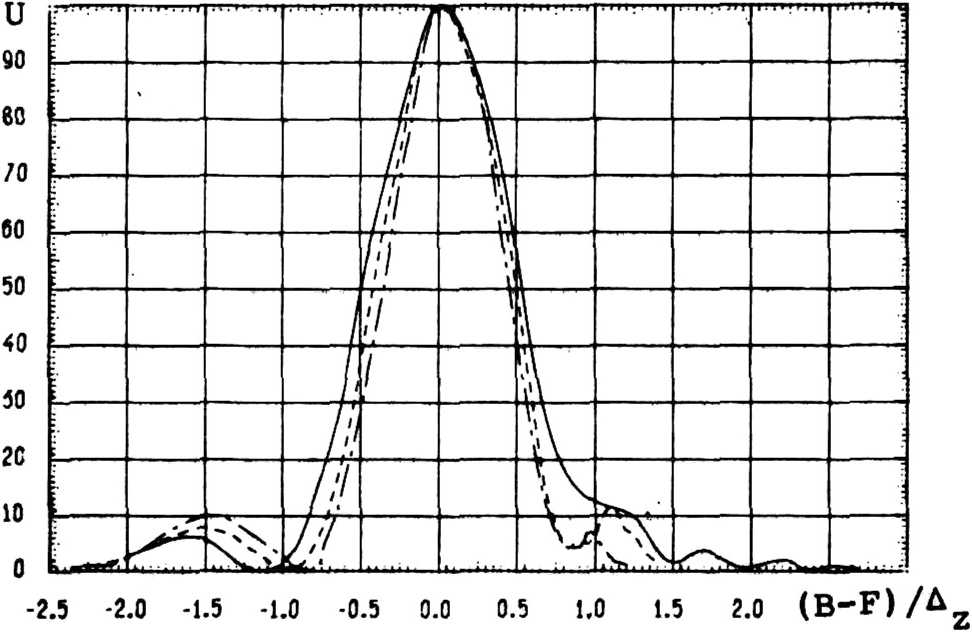
Рис. 2. Распределение интенсивности поля вдоль оптической оси;

△х/х0,%

-------------------   -21.05

----------   -11.54

-.-.-.-.-.  +4.55

Прежде чем переходить к результатам экспериментальных исследований, отметим одно важное свойство дифракционных объективов на поверхностях второго порядка - свойство невзаимности. Дело в том, что для плоского объектива (зонной пластины) возможна перемена положений переднего и заднего отрезка при фиксированном положении ЗП. Например, если ЗП рассчитана на передний отрезок А и задний отрезок В, то меняя их местами (то есть помещая источник излучения на расстоянии В от плоскости ЗП, а приемник излучения - на расстоянии А) работоспособ ность радиообъектива сохранится. Это обусловлено тем, что значения радиусов зон Френеля для зонной пластины не зависят от перестановки А*В. Для неплоских же дифракционных объективов это свойство не выполняется, поэтому при расчете параметров таких объективов необходимо учитывать ориентацию вершины ДО в пространстве относительно расчетных значений А и В.

Однокомпонентный объектив

Однокомпонентный параболический радиообъектив, внешний вид которого приведен на рис. 3, изготавливался на станке с программным числовым управлением. Материалом радиообъектива служил полиэтилен, апертура радиообъектива составляла D/A_OS44, передний отрезок А/Х_О587 задний отрезок В/Х_ОХ43, фокус параболоида F/A_o514.

Рис. 3. Внешний вид дифракционного радиообъектива на параболической поверхности

Частотные свойства параболических радиообъективов характеризуются зависимостями, показанными на рис. 4. Из рис. 4 видно, что указанные зависимости с хорошей точностью совпадают в области отрицательных расстроек длины волны X от расчетной Хо и отличаются лишь на 3-4% в области положительных расстроек X. Совпадение зависимостей В(Х) для зонной пластины и дифракционных параболических объективов обусловлено, по-видимому, тем фактом, что для данных параметров ДО на параболической поверхности укладывается примерно такое же количество эон Френеля, что и для зонной пластины.

Что касается разрешения параболического объектива при внеосевом положении источника излучения, то проведенные экспериментальные исследования показали, что на краю поля зрения для однокомпонентного ДО уширение главного лепестка дифракционного пятна, полученное по первым нулям составляет **4%, а уровень боковых лепестков (интенсивность) находится в диапазоне 5-7% от интенсивности главного лепестка рассеяния. Поле зрения однокомпонентного параболического ДО с D,**44 составляет не менее 30°.

Л

Для доказательства свойств невзаимности "выпуклых" ДО, о чем указывалось выше, были проведены соответствующие эксперименты. Так, например, для однокомпонентного параболического ДО была проведена замена отрезков AZB. Затем исследовано распределение интенсивности поля вдоль оптической оси. Исследования показали, что в этом случае кроме основного максимума интенсивности поля на оптической оси имеется несколько побочных с интенсивностью, сравнимой с амплитудой основного лепестка рассеяния. Следовательно, КПД таких ДО падает, поскольку происходит перераспределение падающего на ДО излучения в несколько максимумов. Кроме того, уже при смещении источника излучения от оптической оси на расстояние △ x**(2-3)R^, где R^ - радиус Эйри, являющийся инвариантом в пространстве Лагранжа-Гельмгольца [8], его изображение "разваливается" - объектив перестает работать, что объясняется несоответствием радиусов зон Френеля и соответ-^твующих отрезков до (нарушение условия таутохроизма).

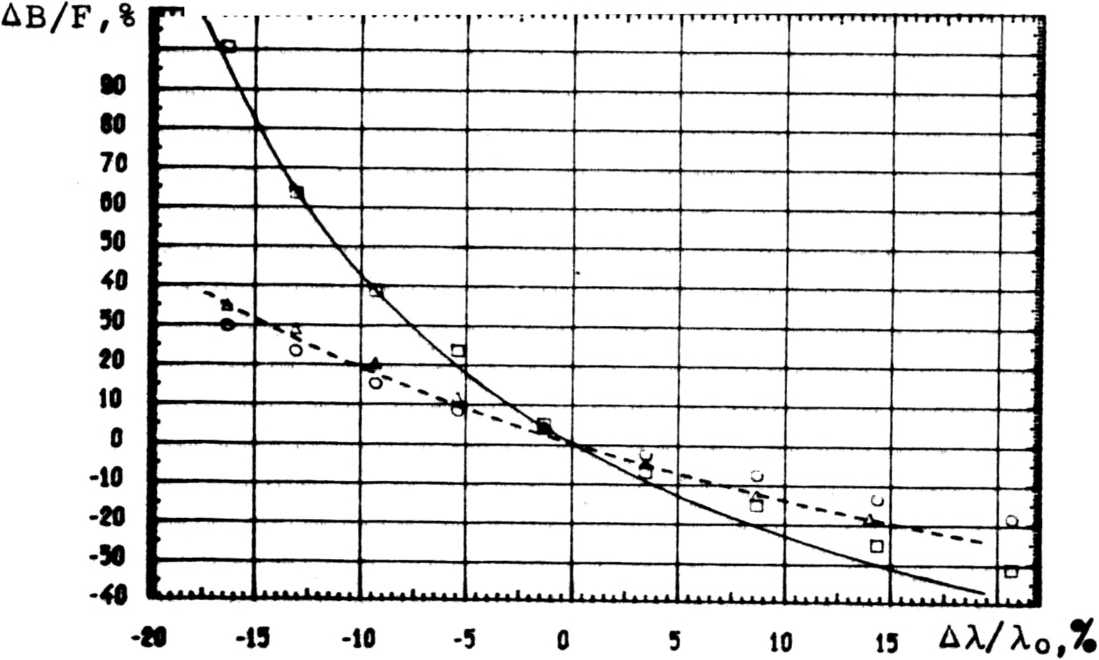
Рис. 4. Частотные свойства дифракционных объективов: -------- зонная пластина АДАД однокомпонентный параболический

ОООО двухкомпонентный параболический

_______________ однокомпонентный параболический

□□□□ с заменой А^В

Двухкомпонентный параболический дифракционный объектив

В работе [9] предложен многокомпонентный ДО на основе зонных пластин Рэ-лея-Вуда, экспериментальные исследования которого показали, что такие системы позволяют значительно увеличить информационные свойства однокомпонентных фокусирующих устройств. Дальнейшее повышение информативных возможностей ДО возможно по пути увеличения, например числа их компонент. Однако этот путь не всегда приемлем по следующим соображениям. Во-первых, значительно возрастает сложность таких устройств в связи с ростом продольных габаритов, взаимной юстировке компонент и т.п, Во-вторых, возрастают потери падающей на объектив мощности излучения, связанные как с переотражением излучения между его компонентами, так и с поглощением излучения в материале объектива (например, в СВЧ диапазоне). Поэтому более рациональным, на наш взгляд, является путь создания двухкомпонентных ДО на неплоских поверхностях.

Двухкомпонентный дифракционный параболический объектив имел такую же апертуру как и однокомпонентный, передний отрезок каждой компоненты ДО составлял А/Л_о ^s47. Расстояние между компонентами объектива L выбиралось в соответствии с выражением [9]:

100A^L

ЛьоГпА + FnaA?

Rn =         4F+nX ' Rn = 4Fbn'

где F - фокусное расстояние параболоида, Ьо - расстояние от вершины параболоида до точки фокусировки вдоль оптической оси, Ьп - проекция n-й зоны Френеля на оптическую ось.

Исследования свойств такого объектива показали следующее. При осевом положении точечного источника излучения обеспечивается такое же разрешение (вдоль и поперек оптической оси), как и для однокомпонентного варианта. В то же время поле зрения двухкомпонентной оптической системы больше, чем у однокомпонентной и составляет не менее 40°. На рис. 4, видно, что частотные свойства описываемого ДО совпадают с аналогичной зависимостью для однокомпонентного варианта.

Заключение

Результаты исследований дифракционных объективов, выполненных на поверхности вращения, образующая которой описывается параболой, позволяют сделать следующие основные выводы:

• -    использование неплоских поверхностей элементов компьютерной (дифракционной) оптики позволяет увеличить поле зрения объектива и число элементов изображения в нем;

• -    двухкомпонентные дифракционные объективы обладают большим полем зрения, чем их однокомпонентные аналоги;

• -    дифракционные объективы могут быть выполнены на поверхностях, образующая которых описывается кривой вращения второго порядка, при этом их фокусирующие свойства сохраняются в широком спектральном диапазоне.