Дифракционные поправки при фокусировке лазерного излучения в отрезок

В работе [1] приведен алгоритм расчета фокусатора в кривую, основанный на геометрооптической аппроксимации оператора распространения комплексной амплитуды света. В этом приближении фокальная кривая представляет собой полосу, имеющую нулевую ширину. Распределение интенсивности в фокальной плоскости характеризуется в этом случае линейной плотностью. Фокальная кривая представляет собой каустику, и поэтому большое значение имеют дифракционные эффекты, которые не учитываются в решении обратной задачи фокусировки. В данной статье предлагается метод расчета фазовой функции фокусатора в отрезок, использующий геометрооптическое приближение вблизи фокусатора, но учитывающий волновые поправки вблизи фокального отрезка.

• 2.    ПОСТАНОВКА ЗАДАЧИ

Пусть лазерное излучение с комплексной амплитудой W_o(u)=vl^(55exp[ik^_o(u)], где Iq(u) - интенсивность освещающего пучка, ^₀(и) — эйконал пучка, k = ^-, X — длина волны падает на фокусатор с апертурой G, расположенной в плоск ости o ’ = (u, v) при z = 0 (рис. 1), который преобразует падающее излучение в поле Wfu) = = W_Q(u)exp [ik^(u)] =\^(3)exp[ikV/₁(T)], где ф(и) — эйконал фокусатора, Ф₁(и) = Ф₀(и) + ф(и) - эйконал непосредственно за плоскостью фокусатора. Задача состоит в отыскании эйконала фокусатора ф(и) , обеспечивающего при z = f в плоскости х = (х, у) формирование светового поля с интенсивностью 1(х), удовлетворяющей условию

/l(x,y)dy = e(x), txl< К(1)

-е2

соответствующему заданному распределению количества энергии 0 (х) в е - окрестности отрезка длины L, лежащего на оси х. При этом корректное задание I₀(u), 1(х) требует выполнения условия нормировки

Т I(x)d2x =/L(u)d2u. _ ООG

Рис. 1. Геометрия задачи фокусировки

Введем Д — дифракционную ширину отрезка. При 2е » Д функция 6 (х) представляет собой линейную плотность [ 1 ] энергии вдоль отрезка. При 2е « Д функция 6 (х) пропорциональна значению интенсивности 1(х, 0) на геометрическом отрезке. Будем искать такое решение ф(и), при котором все лучи, проведенные из произвольной "фокусирующей кривой” u = const пересекают плоскость фокусировки в одной точке фокального отрезка, имеющей координаты:

Г х = к (и)

[у = 0.                                                                                                  (2)

"Фокусирующая кривая" может наглядно интерпретироваться как узкая светящаяся полоска на фокусаторе, видимая из точки наблюдения (х, о, f).

Так как уравнение эйконала выполнено в окрестности фокусатора, то в параксиальном приближении нетрудно получить уравнение наклонов dik к(и) — и дф. v

Г-'э7 = -у позволяющее записать эйконал фокусатора ф(и) в виде

^(u.v) = -           I / к (£) d £ - (u, v).(4)

ZI I Uq             vv

В работе [1] вид фокусирующей кривой однозначно связывался с выполнением геометрической оптики и наличием одного геометрооптического эйконала как вблизи фокусатора, так и в фокальной плоскости. Это приводило лишь к частному случаю "фокусирующей кривой", названной "слоем” и имеющей вид гиперболы. Обобщенное определение (2)-(4) описывает случай, когда геометрооптическая оптика действует в окрестности фокусатора, но переста- ет действовать вблизи фокальной плоскости, например при длине отрезка порядка нескольких Д или наличии всплеска функции 8 (х) на длине порядка Д. При больших фокальных отрезках и плавной функции 8 (х) фокусирующие кривые переходят в слои [1]. Кроме того, геометрооптический подход ограничивается лишь случаем е -*«>, в то время как прикладной интерес представляет фокусировка в отрезок заданной, например, дифракционной ширины.

• 3.    АППРОКСИМАЦИЯ ПРЯМОЙ ЗАДАЧИ

В ПАРАКСИАЛЬНОМ ПРИБЛИЖЕНИИ

В параксиальном приближении интеграла Кирхгофа комплексная амплитуда w(x) в плоскости фокусировки имеет вид:

w(x) _ kexp(ikf) j T/Lt^expliki^tu)] ехр[^-(х - u)²] d²u, 2 л i f     G                             2 f

где ^(tt) — эйконал пучка сразу за фокусатором

^1^ = " 4^+ 7 ;“ K^)d^ (6) 2f ' “о

Пусть апертура фокусатора G ограничена кривыми v = gj(u), v = g2(u) и отрезками прямых и = а, и = Ь, параллельных оси v (рис. 1). Согласно методу дифракционного расчета [2] при фокусировке в отрезок может быть получена дифракционная аппроксимация интеграла (6), основанная на использовании метода стационарной фазы при интегрировании поперек фокусирующей кривой, то есть по переменной и, причем

1(х) = iV^r ^ Х x/l0(u . v)(-^) Иехр(- ^yv)dv|2

*1<“х>             du             f где ux — решение уравнения (2) относительно и.

Формула (7) хорошо описывает дифракционные эффекты в поперечном сечении фокального отрезка, но не вблизи концов, то есть лишь частично уточняет геометрооптические соотношения.

• 4.    РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ ФОКУСИРОВКИ В ОТРЕЗОК

Решение обратной задачи фокусировки в отрезок будем строить на основе дифракционного соотношения, полученного в п. 3. Согласно уравнениям (1), (7) функция 6 (х) должна удовлетворять следующему соотноше-

НИЮ

€ /--- 82^ /------

Л\^т / V Io (u, v)exp(- ^yv)dv|2dy = 0[к(и)]      ,

-е 2яГ gi(u)                 f                        du которое является нелинейным дифференциальным уравнением первого порядка для функции к (и) с граничными условиями: к(а) = - ^ , к(Ь) = ^ . Эйконал фокусатора определяется через функцию к (и) согласно (4). Заметим, что полученный эйконал ^(и ) имеет вид (4), сходный с эйконалом геометрооптического фокусатора, но с существенно другой, не геометрооптической функцией к (и), учитывающей дифракционные поправки.

+ 00

Для сравнения отметим, что в геометрооптическом случае, то есть при в(х) = f 1(х, y)dy, 1х| < = уравнение имеет вид                                                               - ”             ²

dx 1    82 ’

— = —^!— J I_n(u, £)d$ du У[к(и)] _gi(u) °

к(а)= - b, x(b)= k.

В этом случае дифференциальное уравнение для к (и) имеет вид

■ du = Сф^ l^M-BiWD^W-K/u)]

к(а)=- р к(Ь) = | ,(И)

где ФОТ = 2[Si(2^)-Sinc2y)](

SiG?) = / ^^ dx, Sine (0) = Sinffi . ох

Подставляя к(и) в (4), получим выражение для эйконала фокусатора.

• 6.    ЧИСЛЕННЫЙ МЕТОД ДИФРАКЦИОННОГО РАСЧЕТА

Для вычисления поля в фокальной области от фокусатора в отрезок уже недостаточно грубой аппроксимации, рассмотренной в п. 3, однако использование даже параксиального приближения интеграла Кирхгофа (5) не позволяет провести аналитические расчеты.

Численный метод расчета комплексной амплитуды при фокусировке в отрезок основывается на методике вычисления интеграла (5):

W(x) = - exp£ikf) /х/ь (u)exp [ikV*. (u)] expp^-G? - u)²) d²?. 2mj g                        ^2f

Предлагаемый метод численного расчета W(x) состоит в приближении апертуры фокусатора С набором определенного вида апертурных областей Ppi = 1, N, аппроксимации эйконала ^(и) при if е Pj простым аналитическим выражением и последующей заменой интеграла (5) суммой легко вычисляемых интегралов по областям Р.. Рассмотрим подробную реализацию численного метода.

Введем разбиение u., i = 1, N, u0 = a, uN = b отрезка (а, Ь] и приблизим апертуру фокусатора G набором областей Р; = [Uj ], uj х [g^Uj-j), g2(ui_1)] • • = LN- Введем соответствующее разбиение фокального отрезка х; = к(и;), i = О, N, х0 = - t xN = L, где к(и) - функция, описывающая соответствие между точками отрезка фокусировки и "фокусирующими кривыми" на апертуре фокусатора. Для функции х = к(и) используется локальная линейная аппроксимация на сетке up i = О, N. При и е [им, uj полагаем х = к^и), где

           ,

Kj(u) = X. + —--------(и - и ) - t.

(ui~ui-l)              2

Тогда эйконал ^(и) при if £ Р. можно считать определенным согласно формуле

U

♦'^ . -- .

(Uj-Uj.,)    " 2f

Lu

+ (*i-i - 2> f + \-

1    i-1

где ф = 1 f _K(()d$.

1 f a

Полагая I0(u.v)= l^.v), ^,(u ) = ^p.(u) при u e Pp запишем W(x) в виде

«й-^..,^..,^^

где 1 (x) = ? exp[l(5Z25tLti(u_„ }

2                       I

1 +u(y,-x - b))jdu

• ¹    u_H f ²(Uj-«,_,) «2^) ______

LW = f V Io(Uj,v)exp[y yv)dv.

g,(Uj)                    f

Вычисление интеграла Ij (x) сводится к интегралу

• *2          .    *

I = J exp(ioxz+i^x)dx, причем

1 = (С [Vka(x + -)] +iSign(a)S[V^i(x +^)])Г=Х2, Vial                 2a                      2a x=Xj где С (x), S(x) — интегралы Френеля

C(x) = / Cos($2)d{, S(x) = J Sin(t2)d$

° f                 °

l,x>0

Sign(x) =

0, x = 0

—l,x<0.

Интеграл Ij (у) вычисляется на основе метода кусочно-постоянной аппроксимации функции I0(Uj,v) на сетке Vp 1 = 0, k; vQ = g1(Uj),vk = 82^):

L (У) = 2Wuj.v,) / exp[^yv]dv = 1 VIq^.v,) (v, - v, ^Sinc^ (v,-У_м))ехр[^.(у, +v^)]. ^vl-l

В общем случае расчет поля при фокусировке в отрезок производится по формулам (13)—(17). Для оптимизации по скорости вычислений можно учесть, что на поле в точке х = (х, у), лежащей на фокальном отрезке или на одном из перпендикуляров к нему, влияют лишь точки апертуры, лежащие в окрестности соответствующей "фокусирующей кривой” и = к""¹ (х), и, следовательно, суммирование в формуле (13) можно выполнять лишь с учетом некоторой окрестности фокусирующей кривой.

• 7.    РЕЗУЛЬТАТЫ ВЫЧИСЛИТЕЛЬНОГО ЭКСПЕРИМЕНТА

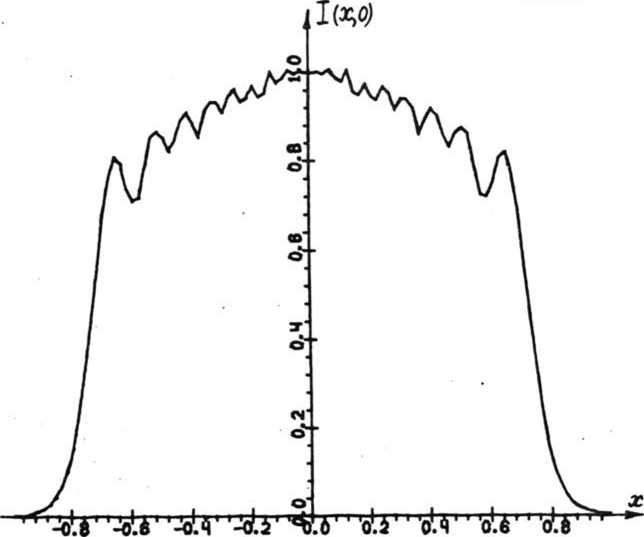
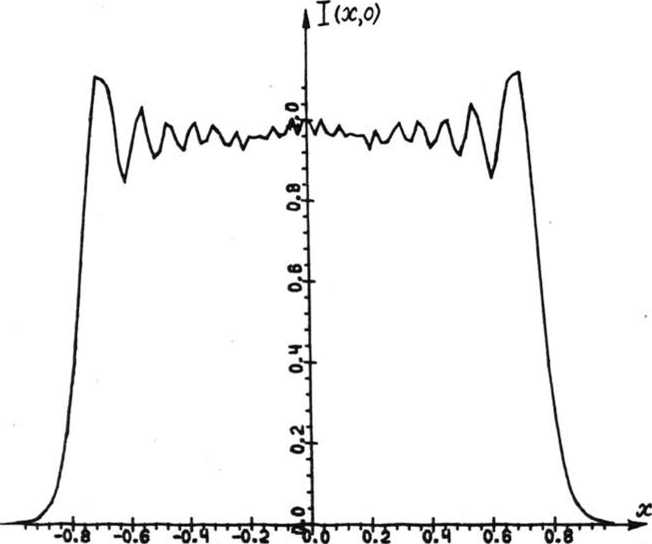
В вычислительном эксперименте проводилось сравнение результатов фокусировки пучка круглого сечения радиуса R в отрезок при использовании геометрооптического эйконала ф(и^ и эйконала с дифракционными поправками ф(и). Эйконал ф(и) рассчитывался для случая 2е«Д, гдеД=^- - ширина дифракционного пятна в центре отрезка фокусировки, соответствующего фокусировке в отрезок с постоянным распределением интенсив ности. Для характеристики качества фокального отрезка используются следующие величины: значение энергетиче

У /l(x)d2x Д L

A L "И ____

ской эффективности -Ей среднеквадратичного отклонения - 6. Величина Е = rVr2-u2 У У „А^и

-RVR2-u2

характеризует долю энергии освещающего пучка, попавшую в окрестность фокального отрезка дифракционной ширины.

Величина 6 = з [— / [I(x, 0) - 1 ]2 dx]% характеризует близость распределения интенсивности на отрезке фо-I L LL кусировки к постоянной величине, где 1 = -У 1(х, 0)dx - среднее значение интенсивности на отрезке фокуси-ровки.-

В таблице 1 для фокусаторов с эйконалами ф(и) и Ф(и) приведены значения энергетической эффективности Е и среднеквадратичного отклонения 6 в зависимости от соотношения длины L отрезка фокусировки с дифракционным размером Д в центре отрезка при фокусировке плоского пучка, WQ(u) = 1 и следующих параметрах: Х = 0,63 мкм, f = 250 мм, R = 3 мм. Данные таблицы 1 наглядно показывают, что при практически одинаковой

Таблица 1

L (мм) Ф<»^ $(u) Е(%) 6 (%) Е(%) 6 (%) 5Д 81,1 24,6 82^ 3sa 10Д 83,4 19,7 84,1 30,1 20Д 83,9 15^ 85,4 2?a 50Д 84,1 11,9 85,7 23,7 энергетической эффективности фокусатор с дифракционным эйконалом ^(и) позволяет почти в два раза уменьшить среднеквадратичное отклонение интенсивности вдоль отрезка фокусировки. На рисунках 2, 3 приведены графики нормированного распределения интенсивности вдоль отрезка фокусировки с длиной L = ЗОД » 1,6 мм, полученные для фокусаторов с эйконалами ^(и) и V'fu) соответственно. Сравнение рис. 2 и рис. 3 показывает, что геометрооптический эйконал реально дает снижение интенсивности по краям, а эйконал с дифракционными поправками обеспечивает более близкое к равномерному распределение.

Рис. 2. Распределение нормированной интенсивности вдоль отрезка фокусировки от геометрооптического фокусатора

Рис. 3. Распределение нормированной интенсивности вдоль отрезка фокусировки от фокусатора с дифракционными поправками

В таблице 2 приведены результаты, полученные при фокусировке гауссового пучка, W„(u)- exp(-—-») при

2 о тех же физических параметрах и а = 1,98 мм. Данные таблицы 2 показывают, что при фокусировке гауссового пучка фокусатор с дифракционным эйконалом ф(и) также обеспечивает более близкое к равномерному распределение, однако уменьшение среднеквадратичного отклонения интенсивности вдоль отрезка фокусировки менее значительно, чем при фокусировке плоского пучка.

Таблица 2

L (мм)	фД		?(и)
	Е(%)	6 (%)	Е(%)	8 (%)
5Д	89,6	20,6	90,5	25,8
10Д	91,4	15,4	923	21,6
20Д	92,8	12,5	93 Д	18,7
5 ОД	93,5	13,4	93,6	16,2